Give the perpendicular slope of the given line y=8/3x-4
Answers
To calculate the perpendicular slope, the steps are the following:
• Step 1: Find the original slope of the line
,• Step 2: Use the condition for the perpendicular slope, to find the perpendicular slope.
Step 1. To find the slope of the given line
\(y=\frac{8}{3}x-4\)we need to compare this with the slope-intercept equation
\(y=mx+b\)where m is the slope and b is the y-intercept of the line. Thus, we can see that the number that accompanies the x represents the slope. And in this line
\(y=\frac{8}{3}x-4\)That number is 8/3. I will call this the slope m1:
\(m_1=\frac{8}{3}\)Step 2. The condition for two lines m1 and m2 to be perpendicular is:
\(m_1\times m_2=-1\)Since in this case we know the original slope m1, and we are looking for perpendicular slope m2, we substitute m1, and solve for m2:
\(\frac{8}{3}\times m_2=-1\)Solving for m2, we need to multiply each side of the equation by 3/8:
\(\frac{3}{8}\times\frac{8}{3}\times m_2=-1\times\frac{3}{8}\)On the left side we are only left with m2, and on the right side we are left with -3/8:
\(m_2=-\frac{3}{8}\)Answer: -3/8
Related Questions
positive even numbers less
than 10
Answers
Answer:
{2, 4, 6, 8}
Step-by-step explanation:
Even numbers are of the form 2n, where n is any integer. If you want positive even numbers less than 10, you require ...
0 < 2n < 10
0 < n < 5 . . . . . . divide by 2
That is, n = {1, 2, 3, 4}, so 2n = {2, 4, 6, 8}.
The positive even integers less than 10 are {2, 4, 6, 8}.
In such cases some time positive no. is less than 10 either more than ten
Step-by-step explanation:
for example 2 is less than ten and 2 is a positive even no.
2nd example 12 is also a positive even no. but more than 10
so we can say for 1 to 9 positive no. are less that ten but 11to infeniti is more than ten
If my answer is correct so like me
6th grade math ok thanks

Answers
192.78
Hope this helps!
✧◝(⁰▿⁰)◜✧
Answer:
192.78
Step-by-step explanation:
0.34 X 567 = 192.78
PlEASE NEED HELP FAST!!!!

Answers
The key features of this quadratic relation y = -3x² - 24x - 36 include;
y-intercept = (0, -36)x-intercept: (-6, 0) and (-2, 0).The equation of the axis of symmetry is x = -4.The vertex is (-4, 12).This quadratic relation has a maximum value of 12.What is the graph of a quadratic function?In Mathematics and Geometry, the graph of a quadratic function would always form a parabolic curve because it is a u-shaped.
Since the leading coefficient (value of a) in the given quadratic function y = -3x² - 24x - 36 is negative 16, we can logically deduce that the parabola would open downward and the x-intercept (roots) is given by the ordered pair (-6, 0) and (-2, 0).
When x = 0, the y-intercept can be determined as follows;
y = -3x² - 24x - 36
y = -3(0)² - 24(0) - 36
y = -36
Axis of symmetry, Xmax = -b/2a
Axis of symmetry, Xmax = -(-24)/2(-3)
Axis of symmetry, Xmax = -4
For the vertex, we have:
y(-4) = -3x² - 24x - 36
y(-4) = -3(-4)² - 24(-4) - 36
y(-4) = 12
In conclusion, the quadratic function has a maximum value at 12.
Read more on quadratic functions here: brainly.com/question/29499209
#SPJ1

A mover places a cylindrical container on a dolly, as shown. Calculate the angle of elevation, U,
from the base of the dolly to the ground.
A. 52.0°
B. 38.0°
C. 38.6°
D. 51.4°
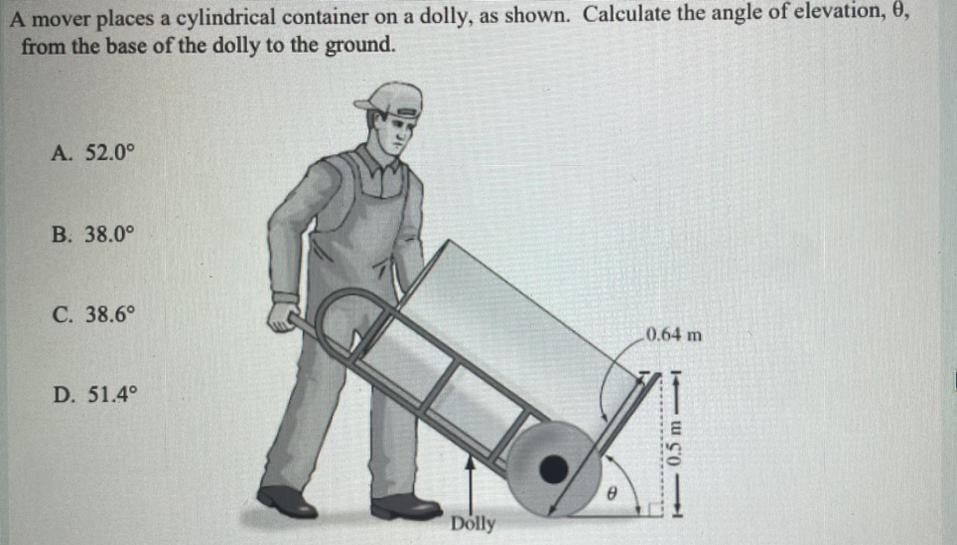
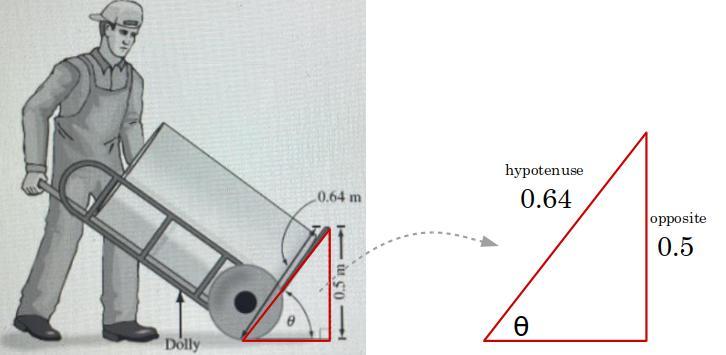
Answers
Check the picture below.
\(\sin( \theta )=\cfrac{\stackrel{opposite}{0.5}}{\underset{hypotenuse}{0.64}} \implies \sin^{-1}(~~\sin( \theta )~~) =\sin^{-1}\left( \cfrac{0.5}{0.64} \right) \\\\\\ \theta =\sin^{-1}\left( \cfrac{0.5}{0.64} \right)\implies \theta \approx 51.4^o\)
Make sure your calculator is in Degree mode.
Please help, I don't know what this is, thank you
Describe these points with a double inequality

Answers
These points can be described the following double inequality: -3≤x≤13.
InequalitiesInequality is a mathematical expression that does not present equality between both sides. It is represented by symbols: <, ≤, > and ≥.
When the variable x is between the both extremes, the inequality will be called double inequality. Therefore, the double inequality can be written in the form below .
a<x<b is equivalent to x>a and x<ba>x>b is equivalent to x<a and x>ba≤x≤b is equivalent to x≥a and x≤ba≥x≥b is equivalent to x≤a and x≥bAs the interval is represented by a closed dot, your interval inequality must be represented by signs ≤ or ≥.
Thus, the points of this question can be described as: -3≤x≤13.
Read more about the double inequality here:
https://brainly.com/question/13707794
The radius of the base of a cylinder is expanding at a constant rate of 3 mm/min. If the height of
the cylinder is a constant 20 mm, find the rate at which the VOLUME of the cylinder is changing at the
moment when the radius of the base of the cylinder is 10 mm. Also find the rate at which the SURFACE
AREA of the cylinder is changing at this same moment.
(V = r²h, SA=2лrh+2rr²)
I’m getting 1800pi mm^3/min for volume and 360pi mm^2/min for surface area but I’m not sure if it’s correct
Answers
The rate at which the volume of the cylinder is changing is 600 mm^3/min, and the rate at which the surface area is changing is 240π mm^2/min.
To find the rate at which the volume and surface area of the cylinder are changing, we can use the given formulas for volume and surface area and differentiate them with respect to time. Let's calculate the rates at the moment when the radius of the base is 10 mm.
Given:
Radius rate of change: dr/dt = 3 mm/min
Height: h = 20 mm
Radius: r = 10 mm
Volume of the cylinder (V) = \(r^2h\)
Differentiating with respect to time (t), we have:
dV/dt = 2rh(dr/dt) + \(r^2\)(dh/dt)
Since the height of the cylinder is constant, dh/dt = 0.
Substituting the given values:
dV/dt = 2(10)(20)(3) + (10^2)(0)
dV/dt = 600 + 0
dV/dt = 600 mm^3/min
Therefore, the rate at which the volume of the cylinder is changing at the given moment is 600 mm^3/min.
Surface area of the cylinder (SA) = 2πrh + 2π\(r^2\)
Differentiating with respect to time (t), we have:
dSA/dt = 2πr(dh/dt) + 2πh(dr/dt) + 4πr(dr/dt)
Again, since the height of the cylinder is constant, dh/dt = 0.
Substituting the given values:
dSA/dt = 2π(10)(0) + 2π(20)(3) + 4π(10)(3)
dSA/dt = 0 + 120π + 120π
dSA/dt = 240π mm^2/min
Therefore, the rate at which the surface area of the cylinder is changing at the given moment is 240π mm^2/min.
For more such questions on cylinder
https://brainly.com/question/28247116
#SPJ8
NEED HELP ASAP!!!
A plane is flying 4200 m above the ground level. the angle of elevation from the control tower to the plane is 15.3°.
what is the horizontal distance from the plane to the control tower?
round your answer to the nearest tenth.

Answers
Answer:
The horizontal distance from the plane to the control tower is approximately 7983.6 meters.
Step-by-step explanation:
To find the horizontal distance from the plane to the control tower, we can use trigonometry.
We know that:
The angle of elevation from the control tower to the plane is 15.3°
The height of the plane above the ground level is 4200 m
We can use the tangent function to find the horizontal distance:
Distance = (Height) / (tan(Angle of Elevation))
Distance = 4200 / (tan(15.3))
Using a calculator or a table of tangent values, we can approximate the horizontal distance to be approximately 7983.6 meters.
Rounding to the nearest tenth, we get 7983.6m ≈ 7983.6m
So the horizontal distance from the plane to the control tower is approximately 7983.6 meters.
1. Find the perimeter of the rectangle.
4in w 7in L
O11 in.
O22 in.
O28 in.
O56 in.
Answers
Answer:
(b) 22 in
Step-by-step explanation:
You want the perimeter of a rectangle with side lengths 4 inches and 7 inches.
PerimeterThe perimeter of a rectangle is the sum of the lengths of its sides. Your rectangle has two sides that are 4 inches, and two sides that are 7 inches. The perimeter is the sum of these lengths:
P = 4 in + 4 in + 7 in + 7 in
P = 22 in
The perimeter of the rectangle is 22 inches.
__
Additional comment
We can save a math operation by recognizing the sum can be arranged to ...
P = (4 in +7 in) +(4 in +7 in) = 2(4 in +7 in)
This is evaluated using one sum and one product, rather than the three sums we need if we simply add the lengths of the four sides.
This is why the usual formula for the perimeter of a rectangle is ...
P = 2(L +W)
Parallelogram A B C D with sides A B and D C parallel and sides B C and A D parallel. Angle B has measure 63 degrees and side B C has length 10. A line segment connects vertex C to base A D at a right angle.
If AB = 9 and AB ∣∣∣∣ DC
, what is the perimeter of ABCD?
Answers
The perimeter of parallelogram ABCD is 43.49 units.
How do we calculate?
We know that BC = 10, so we can use the Pythagorean theorem to find the length of AD:
AD^2 = BC^2 + x^2
AD^2 = 10^2 + x^2
AD^2 = 100 + x^2
AD = √(100 + x^2)
Perimeter = AB + BC + CD + AD
Perimeter = 9 + 10 + 9 + √(100 + x^2)
angle B has measure 63 degrees and we can use the sine function to find x:
sin 63 = x / √(100 + x^2)
x / √(100 + x^2) = sin 63
x = sin 63 * √(100 + x^2)
x = 0.819 * √(100 + x^2)
x / 0.819 = √(100 + x^2)
x^2 / 0.6761 = 100 + x^2
x^2 / 0.6761 - x^2 = 100
x^2 * (1 / 0.6761 - 1) = 100
x^2 = 100 / (1 / 0.6761 - 1)
x = √(100 / (1 / 0.6761 - 1))
x = 5.48
We then substitute x back into the expression for the perimeter:
Perimeter = 9 + 10 + 9 +√(100 + x^2)
Perimeter = 9 + 10 + 9 + √(100 + 5.48^2)
Perimeter = 9 + 10 + 9 +√(100 + 30.0304)
Perimeter = 43.49
Learn more about Pythagorean theorem at: https://brainly.com/question/21332040
#SPJ1
QUESTION:-↓
The dimensions of a room are 12.5 m by 9 m by 7 m. there are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at Rs. 3.50 per square meter.
no spam!
Answers
Given dimensions of the room:
Length: \(\displaystyle\sf 12.5 \,m\)
Width: \(\displaystyle\sf 9 \,m\)
Height: \(\displaystyle\sf 7 \,m\)
Area of each wall:
\(\displaystyle\sf Area_1 = 12.5 \times 7 = 87.5 \,m^2\)
\(\displaystyle\sf Area_2 = 12.5 \times 7 = 87.5 \,m^2\)
\(\displaystyle\sf Area_3 = 9 \times 7 = 63 \,m^2\)
\(\displaystyle\sf Area_4 = 9 \times 7 = 63 \,m^2\)
Area of each door:
\(\displaystyle\sf Area_{\text{door}} = 2.5 \times 1.2 = 3 \,m^2\)
Area of each window:
\(\displaystyle\sf Area_{\text{window}} = 1.5 \times 1 = 1.5 \,m^2\)
Total area occupied by doors:
\(\displaystyle\sf Total_{\text{doors}} = 2 \times Area_{\text{door}} = 2 \times 3 = 6 \,m^2\)
Total area occupied by windows:
\(\displaystyle\sf Total_{\text{windows}} = 4 \times Area_{\text{window}} = 4 \times 1.5 = 6 \,m^2\)
Total wall area excluding doors and windows:
\(\displaystyle\sf Total_{\text{wall\,area}} = (Area_1 + Area_2 + Area_3 + Area_4) - Total_{\text{doors}} - Total_{\text{windows}}\)
\(\displaystyle\sf = (87.5 + 87.5 + 63 + 63) - 6 - 6\)
\(\displaystyle\sf = 275 - 6 - 6\)
\(\displaystyle\sf = 263 \,m^2\)
Cost of painting the walls:
\(\displaystyle\sf Cost_{\text{painting}} = Total_{\text{wall\,area}} \times 3.50\)
\(\displaystyle\sf = 263 \times 3.50\)
\(\displaystyle\sf = 920.50 \,Rs\)
Therefore, the cost of painting the walls of the room at Rs. 3.50 per square meter is Rs. 920.50.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
which graph shows the inverse of the function f (x) = x^3?

Answers
Taking cube root on both sides, we get
\(\sqrt[3]{y}=x\)\(R\text{eplace x=}f^{-1}(y)\text{ since we taken y=f(x)}\)\(f^{-1}(y)=\sqrt[3]{y}\)\(\text{ Replace x=y, we get }f^{-1}(x)=\sqrt[3]{x}\text{ is the }inverse\text{ function of f(x)=}x^3\text{.}\)The given two graphs are parabolic graphs. Those are not the inverse of the given function.
\(\text{The graph of the function is }f^{-1}(x)=\sqrt[3]{x}\text{ is}\)Hence this is the required graph.

A tank is in the shape of a cylinder of radius 15 cm and height 50 cm.Work out the volume of the tank.
Answers
Answer: \(11250\pi \\\) cm^3
Step-by-step explanation:
This could be solved with integral calculus or simple arithmetic.
If you need to show the work in calculus, let me know, otherwise, here's the easiest way to reach the answer:
Volume of a solid is equal to the area of its 2D projection multiplied by its height, assuming that it's uniform throughout its entire height. Fortunately, a cylinder is uniform throughout its height.
What is a cylinder's 2D projection? A circle!
Area of a circle = \(\pi r^{2}\)
r = 15
Area = 225pi cm^2
Now, we multiply the area of the 2D projection by the height of the cylinder.
225pi * 50 = 11250pi cm^3
When factored, the trinomials x2 + 4x − 21 and x2 + 11x + 28 have one binomial factor in common. What is this factor?
x − 7
x + 7
x − 5
x + 5
Answers
Answer:
x + 7
Step-by-step explanation:
x2 + 4x − 21
set equal to 0
x2 + 4x − 21 = 0
factor
(x - 3) (x + 7)
x2 + 11x + 28
set equal to 0
x2 + 11x + 28 = 0
factor
(x + 4) (x + 7)
What is the perimeter of the shape below? Use 3.14 for pi. Answer with numbers only, no units.
DO NOT ROUND THE ANSWER

Answers
Step-by-step explanation:
The circumference of a WHOLE circle = pi * d
you have 1/2 of this and d = 10 ft
so 1/2 pi * 10 PLUS the two straight sides + 8+6
1/2 pi * 10 + 8 + 6
5 pi + 8 + 6
5 * 3.14 + 14 = 29.7 ft
The diagonals of parallelogram ABCD intersect at P. Which statements must be true? Select all that apply.

Answers
The statements that will be true about parallelogram ABCD are: A, B, D, and E.
Properties of a Parallelogram -
Diagonals of a parallelogram bisect each other into congruent segments.
Opposite angles and sides of a parallelogram are always congruent.
Alternate interior angles are always congruent in measure.
Thus, the following would be true of parallelogram ABCD:
AP ≅ CP (congruent segment's of a bisected diagonal)
BC ≅ AD (congruent opposite sides)
∠CAD ≅ ∠ACB (congruent angles)
∠BPC ≅ ∠APD (congruent angles)
Therefore, the statements that will be true about parallelogram ABCD are: A, B, D, and E.
Learn more about parallelogram on:
brainly.com/question/3050890
#SPJ1
Select all the expressions that are greater than 1
1/10 ÷ 3
2 2/3 ÷ 1 2/3
5/7 ÷ 1/2
12 ÷ 1/2
2/7 ÷ 3/7
Answers
2/ 2/3 divided by 1 2/3= 1 3/5, yes
5/7 divided by 1/2= 1 3/7, yes
12 divided by 1/2= 24, yes
2/7 divided by 3/7= 2/3, no
The Maryland Department of Transportation reported the following data on driving Speed (miles per hour, mph) and fuel efficiency or Mileage (miles per gallon, mpg), for ten mid-size automobiles: 1 23 4 5 6 7 89 10 Automobile Speed (mph 30 50 40 55 30 25 60 25 50 55 Mileage (mpg)2 25 25 2330 32 2 32625 a. Compute the sample bivariate correlation coefficient. b. Interpret the strength (magnitude) and sign (direction) of the sample bivariate correlation coefficient. Test whether the population bivariate correlation coefficient difers significantly from zero at α-0.01. c.State the null and alternative hypotheses associated with the test. d. What is the calculated value of the associated test statistic? e. What is the critical value of the associated test statistic? f.State your decision regarding the null hypothesis. g. State your conclusion (meaning, describe what the decision means in this problem)
Answers
On solving the provided question we can say that - correlation coefficient of the question is r = \(\frac{S_{xy} }{\sqrt{S_{xx} S_{yy} } }\) = -0.91
What is correlation coefficient ?The Pearson's correlation coefficient, also known as the Pearson's r, Pearson's product-moment correlation coefficient, bivariate correlation, or simply correlation coefficient, is a statistical indicator of the linear relationship between two sets of data.
\(S_{xx} =\)∑\(x^2\) - (∑x\()^2\) /n = 19300- ((420)^2 /10)= 1660
\(S_{yy} =\) ∑\(y^2\) (∑y\()^2\)/n = 7454- ((270)^2 /10) = 164
\(S_{xy} =\)∑\((xy)^2\)/n -475
The correlation coefficient is:
r = \(\frac{S_{xy} }{\sqrt{S_{xx} S_{yy} } }\) = -0.91
To know more about correlation coefficient visit:
https://brainly.com/question/15577278
#SPJ4
I struggle with math and am having difficulty solving this problem. Please only solve if you definitively know the answer. Thank you!

Answers
The equivalent expression of \(6^\frac 25\) is \((\sqrt[5]{6})^2\)
How to determine the equivalent expression?The expression is given as:
\(6^\frac 25\)
The law of indices states that:
\(a^\frac mn = (\sqrt[n]{a})^m\)
Using the above as a guide, we have:
\(6^\frac 25 = (\sqrt[5]{6})^2\)
Hence, the equivalent expression of \(6^\frac 25\) is \((\sqrt[5]{6})^2\)
Read more about equivalent expression at:
https://brainly.com/question/24242989
#SPJ1
In AUVW, UW is extended through point W to point X, mZUVW = (3x + 16)°, mZWUV = (2x + 8), and mZVWX= (8x - 18). Find mZWUV.
Answers
Let's draw the figure to better understand the problem.

What is the amount of discount

Answers
Answer: 26.40
Step-by-step explanation:
Given the exponential function f (x) and the logarithmic function g(x), which of the following statements is true?
a. As x→∞, f (x)→∞ and g(x)→∞.
b. As x→∞, f (x)→∞ and g(x)→1.
c. As x→∞, f (x)→3 and g(x)→1.
d. As x→∞, f (x)→3 and g(x)→∞.
HELP!!! ASAP!!! PRE-CALCULUS!!!

Answers
Answer:
a
Step-by-step explanation:
Both the exponential and logarithmic functions tend to infinity.
Billy bought seven cat toys. Each cat toy costs the same amount. He spent a total of $22.75 (a) Write an equation that represents the situation. Use cto represent the cost of each cat toy. (b) Solve for c and justify your solution by checking your answer
Answers
Answer:
A. 22.75 divided by 7 which would equal 3.25 B. the answer would be 3.25 for each cat toy
Step-by-step explanation:
A triangular pyramid has a base area of 74 square inches and a height of 9 inches. Which is closest to the volume of the pyramid?
a 351 cubic inches
b 702 cubic inches
c 224 cubic inches
d 234 cubic inches
Answers
Answer:
702
Step-by-step explanation:
because 74 x 9 = 666 and 702 is close
Solve for x. Assume that lines that appear tangent are tangent.
A 6.9
B 35
C 19
D 26.9

Answers
Answer:
Step-by-step explanation:
b 35
Given h of x equals negative 2 times the square root of x minus 3 end root, which of the following statements describes h(x)?
The function h(x) is increasing on the interval (–∞, 3).
The function h(x) is increasing on the interval (–3, ∞).
The function h(x) is decreasing on the interval (–∞, 3).
The function h(x) is decreasing on the interval (3, ∞).
Answers
Answer:
The function h(x) is decreasing on the interval (3, ∞).
Step-by-step explanation:
Please take a look at the attached image.
You will see a graph of the given function h(x) = -2\(\sqrt{x-3}\). The function is decreasing.
The function starts at 3 and starts to go towards negative infinity on the x-axis. Therefore the function is decreasing on the interval (3, ∞).
2 A sample of two items is selected without replacement from a batch. Describe the (ordered) sample space for each of the following batches: a. The batch contains the items {a, b, c, d}. b. The batch contains the items {a, b, c, d, e, f , g}. c. The batch contains 4 defective items and 20 good items. d. The batch contains 1 defective item and 20 good items.
Answers
Answer:
a.{a b, a c, a d, b c, b d, c d, b a, d c ,d b, c a, d a, c b}
b.{a b, a c, a d, a e ,a f, a g, b c, bd,be,bf,bg,cd,ce,cf,cg,fg,ba,ca,da,ea,fa,ga,cd,db,eb,fb,gb,dc,ec,fc,gc,fe,ge,gf,de,df,dg,ed,fd,gd,ef,eg}
c.{d d, dg, g d, g g}
d.{dg, g d, gg}
Step-by-step explanation:
We have to find the sample space
a. We are given items
{a, b, c, d}
Therefore, the sample space
{a b, a c, a d, b c, b d, c d, b a, d c ,d b, c a, d a, c b}
b. Items
Therefore, the sample space
{a b, a c, a d, a e ,a f, a g, b c, bd,be,bf,bg,cd,ce,cf,cg,fg,ba,ca,da,ea,fa,ga,cd,db,eb,fb,gb,dc,ec,fc,gc,fe,ge,gf,de,df,dg,ed,fd,gd,ef,eg}
c.
Defective items (d)=4
Good items(g)=20
Therefore, the sample space
{d d, dg, g d, g g}
d.
Defective items (d)=1
Good items(g)=20
Therefore, the sample space
{d g, g d, g g}
A circle has diameter of 17 meters. What is its radius?
This is Delta Math
Answers
1. What is the pattern of the numbers in the list?
3, 9, 15,...
Answers
Select the correct answer.
What is the SI unit of time?
A second
B minute
C hour
D day
Answers
The unit of the Sl time is in seconds so the answer is A
(AREA = ES CATETO POR CATETO O BASE POR ALTURA. ENTRE DOS)
Calcula el área de la región sombreada.
a)7 m2
b)8 m2
c)15m2
d)28m2
e)56m2
ayuda pls

Answers
The area of the base of the right triangle is calculated as: d. 28 m².
How to Find the Area of a Right Triangle?The area of a right triangle is expressed as, area = 1/2 × b × h, where we have:
h as the height of the right triangle
b as the length of the base of the right triangle
Given the following about the right triangle:
height of the right triangle (h) = 8 m
length of the base of the right triangle = 7 m
Area of the right triangle = 1/2 × b × h = 1/2 × 7 × 8
Area of the right triangle = 28 m²
Thus, the area of the base of the right triangle is calculated as: d. 28 m².
Learn more about the area of triangle on:
https://brainly.com/question/17335144
#SPJ1