f(x)=2^(2)-18x-20
solve by factoring !!!!!!!
Answers
The roots of the equation are x = 10 and x = -1.
What is factorization ?
Factorization is the process of expressing a mathematical expression or number as a product of its factors or divisors. In other words, factorization involves breaking down a given expression or number into smaller parts or factors that, when multiplied together, give the original expression or number.
For example, consider the number 12. It can be factorized as:
12 = 2 x 2 x 3
This means that 12 can be expressed as the product of its prime factors, which are 2 and 3. Similarly, consider the expression x² - 4. This can be factorized as:
x² - 4 = (x + 2)(x - 2)
This means that the expression x² - 4 can be expressed as the product of its factors, which are (x + 2) and (x - 2).
Factorization is an important tool in algebra and number theory and is used in a variety of applications, including finding the roots of equations, simplifying algebraic expressions, and cryptography.
To solve the equation by factoring, we need to find two numbers whose product is equal to the product of the coefficient of the squared term (which is 2) and the constant term (which is -20), and whose sum is equal to the coefficient of the linear term (which is -18).
The product of 2 and -20 is -40. We need to find two numbers whose product is -40 and whose sum is -18.
After some trial and error, we can see that -20 and 2 are the numbers we need.
Therefore, we can write the equation as:
F(x) = 2x² - 18x - 20
= 2(x² - 9x - 10)
= 2(x - 10)(x + 1)
So the roots of the equation are x = 10 and x = -1.
To know more about factors visit :-
https://brainly.com/question/25829061
#SPJ1
Related Questions
Christine bought lunch 15 times at school this month and spent a total of $49.50. Each of her lunches cost an equal amount
Which equation could Christine use to determine the price of each lunch (p?
15p = 49.50
49.50p = 15
15+p=49.50
49,50 + p = 15
Answers
Answer:
The answer is 15p = 49.50
Answer:
The answer is $3.3
Step-by-step explanation: Because 49.50 divided by 15 is 3.3
Simplify (2.5)(−5)(−4.6). (5 points)
Select one:
a.
−575
b.
−57.5
c.
57.5
d.
575
Answers
hope it helps

Answer:
C. 57.5
Step-by-step explanation:
First you would want to set up the equation. (2.5 x -5 x -4.6) Now you can do 2.5 x -5 which is -12.5, and then you would do -12.5 x -4.6 which is not negative 57.5 because a negative times a negative becomes a positive so your final answer is C. 57.5
Help please I’m confused

Answers
Answer:
it is the 2nd option
Step-by-step explanation:
HELP??? What is the equation of the line in y=mx+b format?

Answers
Answer:
y = 1/2x - 1Step-by-step explanation:
To find the slope, you need to find the y-intercept first (or the place the line crosses over the y-line). After you've found the y-intercept (-1), you need to find the next point that the line crosses. This line has a positive slope, so you'll want to look for the next point towards the right. The next point was 1 up and 2 over.
Answer:
y = 2/5x - 1
Step-by-step explanation:
There are a couple of different ways to figure this out, but since you have a graph, the fastest way is to count the slope, or m in the formula, by counting the rise (units up) over run (units to the right), which is 2/5. Then, find the value of b by finding the y-intercept on the graph, or -1.
a container with a square base, vertical sides, and closed top is to have a volume of 2000 cm 3 . it costs twice as much per square centimeter to make the top and bottom as it does the sides. find the dimensions of the container that will minimize the cost
Answers
Ans .: The dimensions of the container that will minimize the cost are a base with sides of length 16.7 cm and a height of 8.35 cm.
To minimize the cost of the container, we need to find the dimensions that will use the least amount of material. Let's call the length of one side of the square base "x" and the height of the container "h".
The volume of the container is given as 2000 cm^3, so we can write:
V = x^2h = 2000
We need to find the dimensions that will minimize the cost, which is determined by the amount of material used. We know that it costs twice as much per square centimeter to make the top and bottom as it does the sides.
Let's call the cost per square centimeter of the sides "c", so the cost per square centimeter of the top and bottom is "2c". The total cost of the container can then be expressed as:
Cost = 2c(x^2) + 4(2c)(xh)
The first term represents the cost of the top and bottom, which is twice as much as the cost of the sides. The second term represents the cost of the four sides.
To minimize the cost, we can take the derivative of the cost function with respect to "x" and set it equal to zero:
dCost/dx = 4cx + 8ch = 0
Solving for "h", we get:
h = -0.5x
Substituting this into the volume equation, we get:
x^2(-0.5x) = 2000
Simplifying, we get:
x^3 = -4000
Taking the cube root of both sides, we get:
x = -16.7
Since we can't have a negative length, we take the absolute value of x and get:
x = 16.7 cm
Substituting this into the equation for "h", we get:
h = -0.5(16.7) = -8.35
Again, we can't have a negative height, so we take the absolute value of "h" and get:
h = 8.35 cm
Therefore, the dimensions of the container that will minimize the cost are a base with sides of length 16.7 cm and a height of 8.35 cm.
Learn more about :
volume : brainly.com/question/28058531
#SPJ11
My teenage son consumed 8 donuts in one sitting. 8 donuts is ....(a)a lower bound on how many donuts he can eat in one sitting.(b)an upper bound on how many donuts he can eat in one sitting.(c)the exact number of donuts that he can eat in one sitting.(d)none of the other answers is correct.
Answers
The correct option from the given options is (a) a lower bound on how many donuts he can eat in one sitting.
A lower bound is a value which is equal to or greater than the minimum value of a set. In this given scenario, eight donuts are a lower bound on how many donuts a teenager can eat in one sitting. He might be able to eat more than eight donuts in one sitting but he cannot eat less than eight donuts in one sitting because it's a lower limit.
A lower limit or a lower bound is an absolute minimum. It is the minimum number of donuts that the teenager can consume in one sitting. In this scenario, there is a possibility that the teenager might eat more than eight donuts, but the lower limit is eight.
Therefore, the correct option is (a) a lower bound on how many donuts he can eat in one sitting.
To learn more about lower bound: https://brainly.com/question/28725724
#SPJ11
past studies indicate that about 60 percent of the trees in a forested region are classified as softwood. a botanist studying the region suspects that the proportion might be greater than 0.60. the botanist obtained a random sample of trees from the region and conducted a test of the p-value of the test was 0.015. which of the following is the correct interpretation of the p-value?
Answers
Answer:
According to the given data, if it is true that 60 percent of the trees in a forested region are classified as softwood, 0.015 is the probability of obtaining a population proportion greater than 0.6.
Step-by-step explanation:
Past studies indicate that about 60 percent of the trees in a forested region are classified as softwood.
A botanist studying the region suspects that the proportion might be greater than 0.60.
The botanist obtained a random sample of trees from the region and conducted a test of H0:p=0.6 versus Ha:p>0.6.
Therefore, he p-value of the test was 0.015, indicating the past studies.
Hope this helps!
Janie ha $ 3. She earn $1. 20 for each chore he doe and can do fraction of chore. She want to earn enough money to buy a CD for $13. 50
Answers
The inequality to use to represent the numbers of chores Janie could do to have enough money to buy CD is 3 + 1.2c > 13.50
How to solve inequality?In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions.
An inequality expression has the the symbols <, >, ≤ and ≥.
Janie has 3 dollars. She earn $1. 20 for each chore she does and can do fraction of chore. She want to earn enough money to buy a CD for $13. 50.
The inequality that can be use to determine the number of chores c, Janie could do to have enough money to buy CD can be represented as follows:
3 + 1.2c > 13.50
learn more on inequality here:https://brainly.com/question/12052820
#SPJ1

Heres another photo ill
Post the word problem ina minute
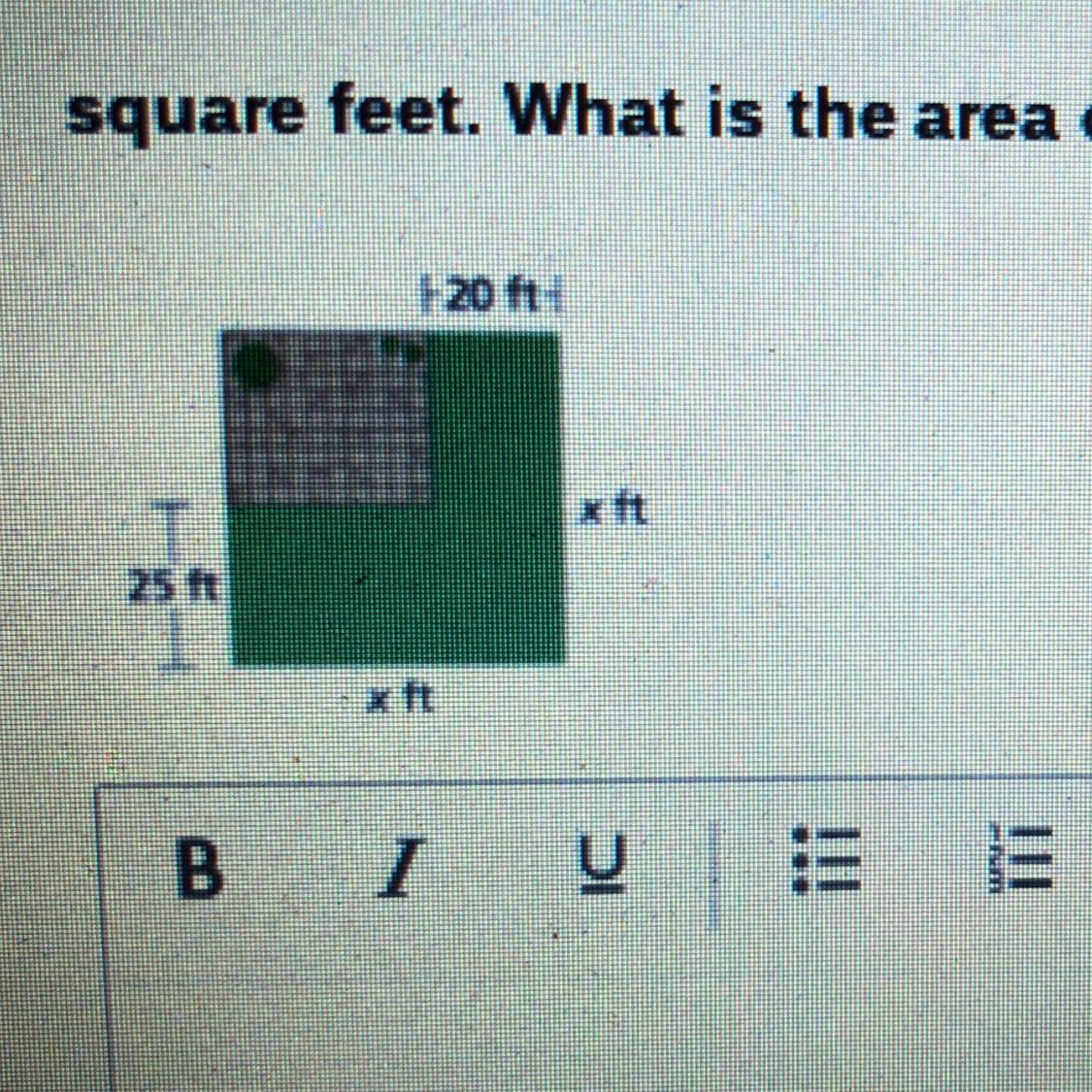
Answers
To Find :
The area of green shaded region in given image.
Solution :
The area of green shaded region is given by :
Area = Area of outer square - Area of inner rectangle
Area = x² - ( x - 20)×( x - 25 )
Area = x² - ( x² - 25x - 20x + 500 )
Area = 45x - 500
Hence, this is the required solution.
Keisha bought 12 pounds of sugar for $7. How many pounds of sugar did she get per dollar?
Answers
Answer:
1.71 pounds of sugar per dollar.
Step-by-step explanation:
To calculate how many pounds of sugar Keisha got per dollar, we divide the total amount of sugar by the total amount of money spent. In this case, she bought 12 pounds of sugar for $7, so we divide 12 by 7:
12 ÷ 7 = 1.71
So, Keisha got 1.71 pounds of sugar per dollar.
Find the 64th term of the arithmetic sequence 2, -3,-8
Answers
Answer:
-313
Step-by-step explanation:
a1=2; d=-5
a64=2-5(64-1)=-313
The 64th term of the arithmetic sequence 2, -3, -8 ... will be -313.
What is Arithmetic sequence?
An arithmetic sequence is the sequence of numbers where each consecutive numbers have same difference.
Given that;
The arithmetic sequence;
⇒ 2 , -3 , -8 ...
Now,
The general equation for nth term of the arithmetic sequence is,
\(T_{n} = a + (n - 1) d\)
Where, The term 'a' represent the first term.
And, 'd' represent the difference between each consecutive numbers.
Here, In the arithmetic sequence 2 , -3, -8;
The first term = 2
The difference = -3 - (2) = - 5
So, To find the 64th term of the arithmetic sequence, we can substitute
n = 64 and a = 2 and d = -5 in above formula as;
\(T_{n} = a + (n - 1) d\)
\(T_{64} = 2 + (64 - 1) (-5)\)
\(T_{64} = 2 + (63 * -5)\)
\(T_{64} = 2 - 315\)
\(T_{64} = -313\)
Thus, The 64th term of the arithmetic sequence 2, -3, -8 ... will be -313.
Learn more about the arithmetic sequence visit:
https://brainly.com/question/6561461
#SPJ5
Jake cuts out five pointed stars. They are different sizes, but they all have the same shape. The size lengths within each star are the same. To find the perimeter of each star. Jake uses the expression 12L + 1/2 - 4L - 8.5 + 2L + 8, where L is the side length of the star.
Find the perimeter of a star with side length 6 inches
Answers
Answer:
Perimeter of the star = 60 inches
Step-by-step explanation:
Given:
12L + 1/2 - 4L - 8.5 + 2L + 8
Where,
L = side length of the star
Find the perimeter of a star with side length 6 inches
L = 6 inches
Perimeter of the star = 12L + 1/2 - 4L - 8.5 + 2L + 8
= 12(6) + 1/2 - 4(6) - 8.5 + 2(6) + 8
= 72 + 0.5 - 24 - 8.5 + 12 + 8
= 60 inches
Perimeter of the star = 60 inches
??????????????????????

Answers
How do you interpret a p-value in the context of a word problem? Please provide a few examples!
Answers
Interpreting a p-value in the context of a word problem involves understanding its significance and its relationship to the hypothesis being tested.
The p-value represents the probability of obtaining the observed data (or more extreme) if the null hypothesis is true.
Here are a few examples of interpreting p-values in different scenarios:
1. Hypothesis Testing Example:
Suppose you are conducting a study to test whether a new drug is effective in reducing blood pressure.
The null hypothesis (H0) states that the drug has no effect, while the alternative hypothesis (Ha) states that the drug does have an effect.
After conducting the study, you calculate a p-value of 0.02.
Interpretation: The p-value of 0.02 indicates that if the null hypothesis (no effect) is true, there is a 2% chance of observing the data (or more extreme) that you obtained.
Since this p-value is below the conventional significance level of 0.05, you would reject the null hypothesis and conclude that there is evidence to support the effectiveness of the drug in reducing blood pressure.
2. Acceptance Region Example:
Consider a manufacturing process that produces light bulbs, and the company claims that the defect rate is less than 5%.
To test this claim, a sample of 200 light bulbs is taken, and 14 of them are found to be defective.
The hypothesis test yields a p-value of 0.12.
Interpretation: The p-value of 0.12 indicates that if the true defect rate is less than 5%, there is a 12% chance of obtaining a sample with 14 or more defective light bulbs.
Since this p-value is greater than the significance level of 0.05, you would fail to reject the null hypothesis.
There is not enough evidence to conclude that the defect rate is different from the claimed value of less than 5%.
3. Correlation Example:
Suppose you are analyzing the relationship between study time and exam scores.
You calculate the correlation coefficient and obtain a p-value of 0.001.
Interpretation: The p-value of 0.001 indicates that if there is truly no correlation between study time and exam scores in the population, there is only a 0.1% chance of obtaining a sample with the observed correlation coefficient.
This p-value is very low, suggesting strong evidence of a significant correlation between study time and exam scores.
In all these examples, the p-value is used to assess the strength of evidence against the null hypothesis.
It helps determine whether the observed data supports or contradicts the hypothesis being tested.
To know more about p-value refer here:
https://brainly.com/question/32387374#
#SPJ11
the area under the normal curve to the right of muμ equals _______.
Answers
Area under the normal curve to the right of μ = 0.5.
What is the area under the normal curve?A normal distribution curve has a 1.0, or 100%, area under it. The curve of a normal distribution is symmetrical about the mean. Therefore, half of the total area under a normal distribution curve is located on the left side of the mean, and half is located on the right side of the mean.
According to question:The normal curve is divided into two equal parts with the mean lying in the center. The area of the normal curve is equal to 1 and it is divided into two equal parts which means that area on either side of the mean is 0.5.
Final answer: Hence, the area under the normal curve to the right of
μ = 0.5.
To learn more about the area under the normal curve visit:
brainly.com/question/27271372
#SPJ4
Here is the picture it says xxxxxxxxxxxxxxxxxxx

Answers
Answer:
Step-by-step explanation:
given: 5^3/5^7
= 1/5^(7-3)
= 1/5^4
= 1/625
final answer: 1/625
Answer:
\(5^{-4}\)
Step-by-step explanation:
using the rules of exponents
• \(\frac{a^{m} }{a^{n} }\) = \(a^{(m-n)}\)
• \(a^{-m}\) = \(\frac{1}{a^{m} }\)
given
\(\frac{5^{3} }{5^{7} }\)
= \(5^{(3-7)}\)
= \(5^{-4}\)
= \(\frac{1}{5^{4} }\) ← if required with a positive exponent
Let f(x)=1/2|x−2|. Write a function g whose graph is a translation 7 units to the left of the graph of f.
Answers
Answer:
g(x) = -2(x - 6) - 7
Step-by-step explanation:
Sorry if I'm wrong
Find the area of the shaded region. Can I have the steps explained please?

Answers
Answer:
76.3 cm²
Step-by-step explanation:
step 1
area of circle= πr²= 3.14*5²= 78.6 cm²step 2
area of 60° sector= 60/360*area of circle= 1/6*78.6= 13.1 cm²step 3
Area of equilateral triangle = √3/4a²= √3/4*5²= 10.83 cm²step 4
Area of circle - area of sector + area of triangle= 78.6 - 13.1 + 10.8= 76.3 cm²Please help me in my math problem! Need within 10 minutes!

Answers
The length of the short and long diagonals of the parallelogram to 3 decimal places are 5.244 units and 14.370 units respectively.
What are parallelogram?
Parallelograms are quadrilateral. They have opposite sides equal to each other. Opposite sides are also parallel. The opposite angles are equal to each other.
Therefore, the angles are as follows;
34°34°146°146°Hence,
length of small diagonal = √9²+ 6² - 2(9)(6) cos 34
length of small diagonal = √81 + 36 - 108(0.82903757255)
length of small diagonal = √117 - 89.5360578359
length of small diagonal = √27.5
length of small diagonal = 5.24404424085
length of small diagonal = 5.244 units
5.244² + d² = 2(9² + 6²)
27.499536 + d² = 2(81+36)
d² = 234 - 27.499536
d²= 206.5
d = √206.5
d = 14.3701078632
d = 14.370 units
length of the longer diagonal = 14.370 units
learn more on parallelogram here: https://brainly.com/question/1563728
#SPJ1
help appreciated thanks

Answers
Answer:
No
Step-by-step explanation:
x=(b-5)/c≠(5-b)/c
supposedly
b=6
c=1
x=6-5/1=1
x=5-6/1= -1
1≠ -1
Answer:
No
Step-by-step explanation:
x = b - 5 / L equal to - (5 - b) / L
What is eighty-three hundredths in standard form
Answers
Answer:
.83
Step-by-step explanation:
hundredths means it is a decimal
In fraction form, it means over 100
83/100
.83
Answer:
0.83
Step-by-step explanation:
Just look at the part where it says hundredths or has the "ths" and youl know how to write it. However, not all types of standard forms are the same some have "and" in them and that means that you should put a decimal point.
Find the perimeter. Simplify your answer.
4p-1
4p-1
4p-1
4p-1

Answers
Perimeter is 16p-4
Calculate the value of 0. Write your equation.

Answers
Answer:
θ = 67.4°
Step-by-step explanation:
using the SOHCAHTOA method,
Here opposite is 12 cm, hypotenuse is 13 cm, adjacent is 5 cm.
Using the formula:
\(sin(\beta ) = \frac{oppsoite }{hypotenuse}\)
\(sin(\beta ) = \frac{12}{13}\)
\(\beta = sin^{-1}(\frac{12}{13} )\)
β = 67.4°
Right angle triangle so apply trigonometric identies.
\(\\ \tt\hookrightarrow cos\theta=\dfrac{5}{13}\)
\(\\ \tt\hookrightarrow cos\theta=0.37\)
\(\\ \tt\hookrightarrow \theta=cos^{-1}(0.37)\)
\(\\ \tt\hookrightarrow \theta=68.3\)
The 4th term of a geometric sequence is -25 and the 9th term is 25/32. Find the 15th term
Answers
The 15th element of the geometric sequence generated by exponential function y = 200 · (- 1 / 2)ⁿ⁻¹ is 25 / 2048.
How to determine the value from a geometric sequence
In this question we find the case of geometric sequence, that is, a set of values generated by a exponential function, whose definition is shown below:
y = a · rⁿ⁻¹, n ≥ 1
Where:
a - Value of the first element of the series.r - Common raten - Index of the n-th element of the series.If we know that y₄ = - 25 and y₉ = 25 / 32, then the expression that generates the geometric sequence is:
- 25 = a · r³
25 / 32 = a · r⁸
- 1 / 32 = r⁵
r = - 1 / 2
a = - 25 / r³
a = - 25 / (- 1 / 2)³
a = - 25 / (- 1 / 8)
a = 200
y = 200 · (- 1 / 2)ⁿ⁻¹
And the 15-th term of the geometric series is:
y = 200 · (- 1 / 2)¹⁴
y = 25 / 2048
To learn more on geometric sequences: https://brainly.com/question/17282782
#SPJ1
For every two-dimensional set C contained in R^2 for which the integral exists, let Q(C)=∬c(x^2+y^2dxdy)
If C1={(x,y) : −1 ≤ x ≤ 1, −1 ≤ y ≤ 1} C2 ={(x,y):−1≤x≤1,−1≤y≤1} and C3 = {(x,y):x^2 + y^2 ≤1}, find Q (C1), Q(C2), Q (C3)
Answers
The values of Q(C1), Q(C2), and Q(C3) are 4, 4, and π, respectively.
The concept of the integral is a fundamental part of calculus and it is used to calculate the area under a curve or the volume of a 3-dimensional object. In this context, we will be exploring the integral of a two-dimensional set in the R^2 plane.
For every two-dimensional set C contained in R^2 for which the integral exists, the function Q(C) is defined as the double integral of the function (x^2 + y^2) over the set C. The double integral is a mathematical tool for finding the total volume under a surface.
Let's consider the three sets C1, C2, and C3 and find Q(C1), Q(C2), and Q(C3).
C1={(x,y) : −1 ≤ x ≤ 1, −1 ≤ y ≤ 1}
Q(C1) = ∬C1 (x^2 + y^2) dxdy = ∫^1_{-1}∫^1_{-1} (x^2 + y^2) dxdy = ∫^1_{-1} [(x^2 + y^2)/2]^1_{-1} dx = 4.
C2 ={(x,y):−1≤x≤1,−1≤y≤1}
Q(C2) = Q(C1) = 4.
C3 = {(x,y):x^2 + y^2 ≤1}
Q(C3) = ∬C3 (x^2 + y^2) dxdy = π.
In conclusion, the values of Q(C1), Q(C2), and Q(C3) are 4, 4, and π, respectively.
To learn more about integral, visit
brainly.com/question/18125359#
#SPJ11
which table represents a nonlinear function?

Answers
Answer:
C
Step-by-step explanation:
The x values for all of them are 2, 4, 6. So the amount in between each y value should stay the same for it to be linear. However, in choice C, it goes from 0 to 6 to 16. The interval went from 6 to 10.
the teacher has a small class with only 7 students. the teacher grades their homework and reports scores of: 10, 7, 8, 12, 9, 11, and 13. what is the median?
Answers
Answer:
10
Step-by-step explanation:
To find the median in a set of data, organize the data from least to greatest.
Here, our data is the homework scores, those being:
10, 7, 8, 12, 9, 11, 13
Let's organize them in ascending order, like so:
7, 8, 9, 10, 11, 12, 13
The next step in finding the median is figuring out which number is in the middle. Since the amount of data we have is an odd number (7), there will be only one number in the middle.
We can find that the number in the middle is 10.
Thus, the median of the scores is 10.
Find the approximate sum of the series shown below.

Answers
Answer:
\(The~expression=7(\frac{5}{3})^{(1-1)}+ 7(\frac{5}{3})^{(2-1)}+7(\frac{5}{3})^{(3-1)}+7(\frac{5}{3})^{(4-1)}+7(\frac{5}{3})^{(5-1)}\\~~~~~~~~~~~~~~~~~~~~~~=7(\frac{5}{3})^0+7(\frac{5}{3})^1+7(\frac{5}{3})^2+7(\frac{5}{3})^3+7(\frac{5}{3})^4\\~~~~~~~~~~~~~~~~~~~~~~=7(1)+\frac{35}{3}+7(\frac{25}{9})+7(\frac{125}{27}) +7(\frac{625}{81})\\~~~~~~~~~~~~~~~~~~~~~~=7+\frac{35}{3}+\frac{175}{9}+\frac{875}{27} +\frac{4375}{81} \\\)
\(=\frac{7(81)}{81}+\frac{35(27)}{3(27)} +\frac{175(9)}{9(9)} +\frac{875(3)}{27(3)}+\frac{4375}{81}\\=\frac{7(81)+35(27)+175(9)+875(3)+4375}{81}\\=\frac{10087}{81}\\=124.53086~(approximate)\)
pirya has picked 1 1/2 cups of raspberries, which is enough for 3/4 of a cake how many cups does she need for the whole cae
Answers
Pirya needs 1 1/2 cups of raspberries for 3/4 of a cake, so she needs 1 1/2 * (4/3) = 2 cups of raspberries for the whole cake.
What is fraction?A fraction is a numerical representation of a portion of a total. It consists of two integers, a numerator and a denominator, separated by a line or slash. The numerator reflects the number of equal portions of the whole that are being considered, while the denominator represents the total number of equal parts in the whole. For instance, the fraction "1/2" denotes one of two identical pieces, or half, of the whole. Mathematicians frequently utilize fractions to represent quantities, ratios, and proportions. They are also used in everyday life to signify amounts, such as one-half of a pizza or one-third of a cups of sugar.
How to solve?
she needs 1 1/2 * (4/3) = 2 cups of raspberries for the whole cake.
To learn more about fraction, visit:
https://brainly.com/question/20593515
#SPJ4
(dy/dx) = e^(3x+2y)
solve the differential equation by separation of variables
Answers
