f(x) = 5(x + 1)(x - 1)
How would you write f(x) = 5(x + 1)(x-1) from factored form to standard form

Answers
F(x) = 5x2 - 5
Related Questions
Angle ABC is a straight angle. MAngleDBC = 130° and Ray B E bisects AngleABD. The center of line A C is point B. Two lines extend from point B. One line extends to the left and contains point E. Another line extends up and to the left and contains point D. What is mEBA? °
Answers
Answer:
25°
Step-by-step explanation:
Since ∠DBC = 130°, ∠DBC + ∠ABD = 180° (sum of angles on a straight line is 180°). Solving for ∠ABD:
∠DBC + ∠ABD = 180°
130 + ∠ABD = 180°
∠ABD = 180° - 130°
∠ABD = 50°
∠ABD is bisected by line BE, therefore ∠ABD = ∠EBA + ∠DBE (angle addition postulate).
The angle addition postulate states that if w is the interior of xyz then ∠XYZ = ∠XYW + ∠ZYW
Since E is the interior of ∠ABD, then:
∠ABD = ∠EBA + ∠DBE
But ∠EBA = ∠DBE
∠ABD = 2∠EBA
50 = 2∠EBA
∠EBA = 25°
Answer:
The answer is 25 degrees
Figure ABC has been dilated using a scale factor of 1/2 to produce figure A' B' C'. the origin is at the center of dilation

Answers
The third choice is the one that describes this dilation.
How to convert centimeters into millimeters?
Answers
Answer: Multiply the centimeters number by 10.
Step-by-step explanation: There are 10 millimeters in every centimeter.
write a linear function f with the values f ( - 2 ) = 3 and f ( 5 ) = 7
Answers
You write f (-2) = 3 as (-2, 3) and f (5) = 7 as (5, 7).
The answer for the graph is \(\mathbf{\frac{4}{3}}\textbf{\textit{x}}\mathbf{+\frac{1}{3}}\).
WILL GIVE BRAINLIEST IF RIGHT
The graph below shows the relationship between the number of miles traveled and the time.
Which statement about the unit rate of the graph is true?
A. The unit rate is 1.
B. The unit rate is 30.
C. The unit rate is 1/12.
D. The unit rate is 12.

Answers
Answer:
I think c
Step-by-step explanation:
When y=1 x=12
Answer: The unit rate is 1/12
Step-by-step explanation:
Mrs. Pitts wrote the volume formula as "V=Bh". What does the "B" represent? a The radius of the base b The diameter of the base c The circumference of the base d The area of the base
Answers
D it’s the base.
Shdnxnxhxb
Write your answer as a fraction or whole number.

Answers
Answer:
3/6 which reduces to 1/3
Step-by-step explanation:
you have three chances of getting a braclet our of 6 total chances of prize
What is the equation of the line that passes through point (-1,4) and is perpendicular to the following equation? y= -1/2x - 4

Answers
Answer:
y=2x-4
Step-by-step explanation:
To find an equation perpendicular to another one, you must find the negative inverse of the slope.
In this case, -1/2 has an inverse of -2, but because we're finding the negative inverse, the two negatives cancel out and we get 2, the slope of our perpendicular equation, which crosses the initial equation, making a right angle.
25 points people please help i will mark brainly give 5 stars and give 5 hearts if correct

Answers
second one: false
third one: false
fourth one: true
A(n)______ contains variables,numbers, and at least one operation.
Answers
Answer:
algebraic expression. An expression that contains at least one variable, at least one numbers and at least one operation.
Step-by-step explanation:
Answer:
expressions
Step-by-step explanation:
this is how a definition in a textbook would be written. they just put a blank in
Y = 2/3x + 20
When x = 21
Answers
Answer:
34
Step-by-step explanation:
1. (a) [2pts] Evaluate the the line integral f(x+2y) da + a²dy, where is the curve consists of line segments from (0,0) to (2, 1) and from (2,1) to (3,0). (b) [3pts] Evaluate the line integral F. dr.
Answers
a) The line integral of the given function f(x+2y) da + a²dy along the specified curve can be evaluated by breaking the curve into two segments. The integral over the first segment is 6, and the integral over the second segment is -5/3. The total line integral is 6 - 5/3, which simplifies to 13/3.
b) The line integral of the vector field F. dr can be evaluated by parameterizing the curve and calculating the dot product of F with the derivative of the parameterization. The integral evaluates to 7/2.
a) To evaluate the line integral of f(x+2y) da + a²dy along the given curve, we break the curve into two segments: (0,0) to (2,1) and (2,1) to (3,0). Along the first segment, we parameterize the curve as r(t) = (t, 2t), where t ranges from 0 to 2. Evaluating the integral over this segment gives us 2∫(t+4t)√(1+4) dt = 6. Along the second segment, we parameterize the curve as r(t) = (3+t, 1-t), where t ranges from 0 to 1. Evaluating the integral over this segment gives us ∫(3+t+2(1-t))√(1+4) dt = -5/3. Adding the two results, we get 6 - 5/3 = 13/3.
b) To evaluate the line integral of the vector field F. dr, we need to parameterize the curve. Let's parameterize the curve as r(t) = (t, t²), where t ranges from 0 to 2. The derivative of r(t) with respect to t is dr/dt = (1, 2t). Evaluating the line integral ∫F. dr over the curve gives us ∫(t, t²)⋅(1, 2t) dt = ∫(t+2t³) dt = [t²/2 + 1/2 * (2/4)t^4] evaluated from 0 to 2. Simplifying, we get (2²/2 + 1/2 * (2/4)2^4) - (0²/2 + 1/2 * (2/4)0^4) = 7/2. Therefore, the line integral of F. dr is 7/2.
To learn more about integral click here:
brainly.com/question/31059545
#SPJ11
Tenemos 2 garrafas una al 20% y otra al 30%. Cual es su capacidad de las garrafas si tenemos 12 litros de agua
Answers
Answer:
Cada garrafa tiene una capacidad de 24 litros.
Step-by-step explanation:
Tenemos dos garrafas, definamos V como el volumen que cada garrafa tiene.
Sabemos que una de las garrafas tiene el 20%, entonces el volumen de agua que tiene esta garrafa es:
(20%/100%)*V
Y la otra garrafa tiene el 30%, entonces esta garrafa tiene:
(30%/100%)*V
El volumen total de agua es la suma de esos dos volúmenes, que nos da:
(20%/100%)*V + (30%/100%)*V
Y sabemos que tenemos 12 L de agua, entonces podemos escribir la ecuación:
12 L = (20%/100%)*V + (30%/100%)*V
Ahora podemos resolver esto para V.
12L = 0.2*V + 0.3*V
12L = 0.5*V
12L/0.5 = V
24L = V
Cada garrafa tiene una capacidad de 24 litros.
22. Use a double integral to determine the volume of the region bounded by z = 3 - 2y, the surface y = 1-² and the planes y = 0 and 20.
Answers
To find the volume of the region bounded by the surfaces given, we can set up a double integral over the region in the yz-plane.
First, let's visualize the region in the yz-plane. The planes y = 0 and y = 20 bound the region vertically, while the surface z = 3 - 2y and the surface y = 1 - \(x^2\) bound the region horizontally. The region extends from y = 0 to y = 20 and from z = 3 - 2y to z = 1 - \(x^2\).
To set up the integral, we need to express the bounds of integration in terms of y. From the equations, we have:
y bounds: 0 ≤ y ≤ 20
z bounds: 3 - 2y ≤ z ≤ 1 - \(x^2\)
To find the expression for x in terms of y, we rearrange the equation y = 1 - \(x^2\):
\(x^2\) = 1 - y
x = ±√(1 - y)
Since we are working with a double integral, we need to consider both positive and negative values of x. Therefore, we split the integral into two parts:
V = ∫∫R (3 - 2y) dy dz
where R represents the region in the yz-plane.
Now, let's evaluate the double integral. We integrate first with respect to z and then with respect to y:
V = ∫[0 to 20] ∫[3 - 2y to 1 - \(x^2\)] (3 - 2y) dz dy
To evaluate this integral, we need to express z in terms of y. From the z bounds, we have:
3 - 2y ≤ z ≤ 1 - \(x^2\)
3 - 2y ≤ z ≤ 1 - (1 - y)
3 - 2y ≤ z ≤ y
Now we can rewrite the double integral as:
V = ∫[0 to 20] ∫[3 - 2y to y] (3 - 2y) dz dy
Integrating with respect to z:
V = ∫[0 to 20] [(3 - 2y)z] evaluated from (3 - 2y) to y dy
V = ∫[0 to 20] [(3 - 2y)y - (3 - 2y)(3 - 2y)] dy
Expanding the terms:
V = ∫[0 to 20] (3y - \(2y^2\) - 3y + \(4y^2\) - 6y + 9) dy
V = ∫[0 to 20] (\(2y^2\) - 6y + 9) dy
Integrating:
V = [2/3 * \(y^3\) - \(3y^2\) + 9y] evaluated from 0 to 20
V = (2/3 * \(20^3\) - 3 * \(20^2\) + 9 * 20) - (2/3 * \(0^3\) - 3 * \(0^2\) + 9 * 0)
V = (2/3 * 8000 - 3 * 400 + 180)
V = (16000/3 - 1200 + 180)
V = 1580 cubic units
Therefore, the volume of the region bounded by z = 3 - 2y, y = 1 - \(x^2\), y = 0, and y = 20 is 1580 cubic units.
Learn more about double integral here:
https://brainly.com/question/27360126
#SPJ11
what is the mean difference of the means? enter the nearest whole number.
Answers
The mean difference of the means is a measure of central tendency that quantifies the difference between the means of two data sets. It is calculated by subtracting one mean from the other and taking the absolute value of the result.
The formula for calculating the mean difference of the means is:Mean Difference of the Means = | Mean₁ - Mean₂ |Therefore, to calculate the mean difference of the means, you need to find the means of the two data sets and subtract the smaller mean from the larger mean. The result will be the mean difference between the means.
It is important to note that the mean difference of the means can be positive or negative depending on which mean is larger. So, to enter the nearest whole number, you would need to round the result to the nearest whole number.
You can learn more about mean difference at: brainly.com/question/31323917
#SPJ11
Kevin and Randy Muise have a jar containing 72 coins, all of which are either quarters or nickels. The total value of the coins in the jar is $12.80. How many of each type of coin do they have?
Answers
x+y=72
The next equation sets up the amount of money the coins add up to. The total is 12.80. The equation will model the amount of money contributed by quarters + the amount of money contributed by nickels
.25x + .05y = 12.80
Next just solve for one variable using the first equation and substitute it in
X=72-y, so .25(72-y)+.05y=12.80
18-.25y+.05y=12.80
5.2=.2y
Y=26
Then we put that back into our first equation and get x=46
46 quarters and 26 nickels. This can be checked by plugging into the second equation. .25(46)+.05(26)=12.80
vohyushe says 3he9hr8u28shehdj29dh2ueg 3e
Answers
Answer:
The answer would be 480
A runner ran 2 miles in 10 minutes a year later she ran 2 miles in 11 minutes. What is the percent increase in her running time.
Answers
Answer:
10%
Step-by-step explanation:
1 is ten percent of 10, and 11-10 = 1. Thus the percent increase in her running time is 10 %
Zane changes the oil in his car 4 times each year. What is the ratio of the number of times he changes his oil per month?
Help me please :(
Answers
Answer:
4:3 i think
Step-by-step explanation:
He changes the oil in his car 4 times each year. There are 12 months in one year. He changes the oil every 12 months. Divide 12 by 4. Zane changes the oil in his car every three months.
x: (x + 5) = 4:5 Work out the value of x.
Answers
Answer:x÷(x+5)=4÷5
5x=(x+5)4
5x=4x+20
5x-4x=20
X=20
Step-by-step explanation:
Solve for X round to the nearest tenth if necessary

Answers
Answer:
the answer is 6.9
the answer is.... 6.9
Step-by-step explanation:
to get 6.9 you have to divide 69 by 10
Sine rule
\(\tt \dfrac{US}{sin\:T}=\dfrac{ST}{sin\:U}\)
U = 180 - (69+90)=21°
Input the value:
\(\tt \dfrac{10}{sin\:90}=\dfrac{X}{sin\:21}\\\\X=35.8^o\)
Write y=x^2-18x+83 in vertex form. Then identify the vertex.
Answers
Answer:
\(\boxed{\bold{f(x)=(x-9)^2+2}}\)
Step-by-step explanation:
\(f(x)=a(x-h)^2+k\qquad\qquad h=\dfrac{-b}{2a}\,,\ \ k=f(h)\\\\\\f(x)=x^2-18x+83\quad\implies\quad a=1\,,\ b=-18\\\\h=\dfrac{-(-18)}{2\cdot1}=\dfrac{18}{2}=9\\\\h=f(3)=9^2-18(9)+83=81-162+83=2\\\\\\ \underline{f(x)=(x-9)^2+2}\)
10.
Use the formula P = 2ℓ + 2w. Find the perimeter of a rectangle with a length of 5.6 ft and a width of 6.1 ft.
A. 23.4 ft
B. 22.2 ft
C. 24.4 ft
D. 24.8 ft
Answers
The camp cook made 3 1/2 pints of baked beans. Each serving of beans is 1/2 of a pint. How many servings of beans did the cook make?
Answers
Answer:
The cook made 7 pints
Step-by-step explanation:
Just minus the half pints
The hypotenuse of right angle triangle is 13cm. If one of the other side of the triangle is 1cm shorter than the hypotenuse, calculate the third side of the triangle
Answers
Greetings from Brasil....
From Pythagoras we have
AB² = AC² + BC²
13² = 12² + X²
X = 5
Answer:
5 cm
Step-by-step explanation:
Pythagoras theorem gives us:
\(hypotenuse^{2} = side^{2} + side^{2}\)
We know the hypotenuse is 13 cm.
We know one side is 12 cm.
\(13^{2} = 12^{2} + side^{2}\)
\(169= 144 + side^{2}\)
Subtracting 144 from both sides:
\(25 = side^{2}\)
Reversing the sides:
\(side^{2}=25\)
\(\sqrt{side^{2}}= \±\sqrt{25}\)
\(side = \±\sqrt{25}\)
\(side = \±5\)
Since a distance can't be negative:
\(side=5\)
The third side is 5 cm.
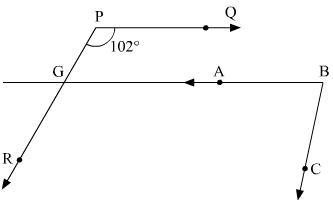
in the fig pq//ab and pr//bc if qpr= 102 degree find angle abc
Answers
The measure of the angle ABC from the diagram is equivalent to 78 degrees.
Line and anglesWe need to find <ABC
Let us produce BA to meet PR at point G.
It is given that BG || PQ
Thus, <RGB and <QPR are corresponding angles.
This shows that <RGB = <QPR since they are corresponding angles.
On the other hand, <QPR = 102 degrees and <ABC are <RGB consecutive interior angles, then:
<ABC + <RGB = 180
<ABC + 102 = 180
<ABC = 180 - 102
<ABC = 78 degrees
Hence the measure of the angle ABC from the diagram is 78 degrees.
Learn more on line and angles here: https://brainly.com/question/25770607
#SPJ1
use the diagram to find the value of x

Answers
Answer:
4
Step-by-step explanation:
18x = 12(x+2)
18x = 12x+24
18x-12x = 24
6x = 24
x = 4
if aaron tunes into his favorite radio station at a randomly selected time, there is a 0.20 probability that a commercial will be playing.
Answers
About 20% of the time Aaron tunes in to his favored station, there will be a commercial playing.
Given info;
The assumption is that over a significant number of days, 20% of the time he tunes in to his favorite station, an ad will be playing. This is based on the idea of relative frequency.
The relative frequency of event A, which is calculated by dividing the number of desired outcomes by the total outcomes, will be off over a large number of experiments, according to the likelihood of an outcome A of a%.
When he dials into his preferred station, there is a 0.2 probability that a commercial will start playing.
The conclusion is that over a long number of days, an advertisement will be playing about 20% of the time he tunes in to his preferred station.
To learn more about probability click here:
brainly.com/question/11234923
#SPJ4
What is the quotient of a quartic and a linear function?
a. quadratic
b. linear
c. cubic
d. quartic
Answers
The quotient of a quartic and a linear function is a quadratic function. This can be proved by dividing a quadratic function by a linear function.
When we divide a quartic function (a function of degree 4) by a linear function (a function of degree 1), the resulting quotient is a quadratic function (a function of degree 2).
The degree of a polynomial function is determined by the highest exponent in the function. In this case, a quartic function has the highest exponent of 4, while a linear function has the highest exponent of 1. Dividing a quartic function by a linear function involves canceling out the terms and reducing the power of the resulting terms.
As a result, the quotient simplifies to a quadratic function with a maximum degree of 2. Therefore, the correct answer is option a. quadratic.
Learn more about Exponents here: brainly.com/question/26296886
#SPJ11
Biologists have found that the number of chirps some types of cricket make per minute depends upon the temperature this relationship can be represented by a linear function when the temperature is 60° Fahrenheit to crickets chirp 92 times per minute if it is 75 Fahrenheit they will chirp 152 times per minute what will the number of chirps be per minute if the temperature is 80 degrees Fahrenheit
Answers
Answer: Crickets make 172 chirps/min at 80 degrees Fahrenheit
Step-by-step explanation:
Step 1
Using the point slope formulae for Linear functions , we have that
y - y1 = m(x - x1)
where x and y are two points representing the temperature and chirps /min respectively
And
m= slope
Step 2 : Finding the slope , m
where x1=60
y1=92
x2= 75
y2=152
m= (y2-y1)/ (x2-x1)
= (152- 92)/(75-60)
=60/15 =4
Bringing down the point/slope formula and imputing the known values to find our equation to show the relationship cricket make per minute and the temperature
y - y1 = m(x - x1)
y - 92= 4(x - 60)
y - 92 = 4x -240
y = 4x - 240 + 92
y = 4x - 148
Step 3
To find the number of chirps be per minute (y) if the temperature is 80 degrees Fahrenheit( x)
y = 4(80) - 160
y = 320 - 148
y = 172 chirps/min at 80 degrees Fahrenheit