f(x) = |4x|-6; reflection in the y-axis (across the y-axis). Just write it out as a function.
Answers
In order to solve this exercise, you need to remember the following Transformation Rules for Functions:
1. When:
\(-f(x)\)The function is reflected across the x-axis.
2. When:
\(f(-x)\)The function is reflected across the y-axis.
In this case, you have this function:
\(f\mleft(x\mright)=|4x|-6\)If this function is reflected across the y-axis, you can apply the second Transformation Rule for Functions explained before. Then, you get that the answer is:
\(f(x)=|-4x|-6\)Related Questions
I need help please.

Answers
Answer:
A) c(x)=2x+60
$74
Step-by-step explanation:
A) c(x)=2x+60
$74
Which triangle is a reflection of the green triangle
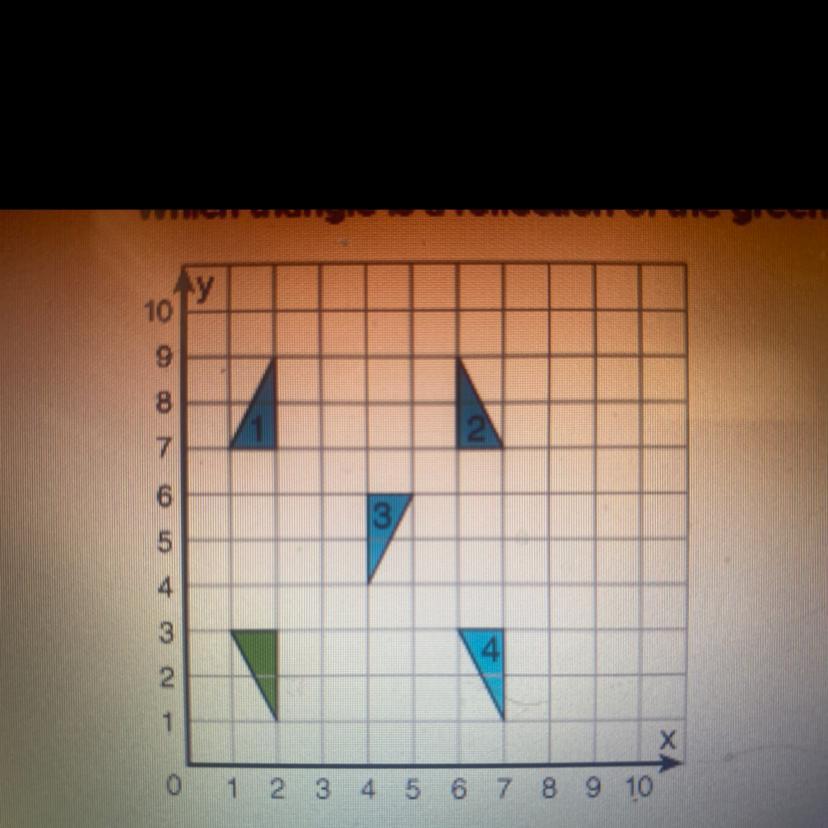
Answers
Tthe triangle that is a reflection of the green triangle is figure 1
Which triangle is a reflection of the green triangleFrom the question, we have the following parameters that can be used in our computation:
The figures
Where, we have:
Figure 1 and the green figure have the opposite orientationFigure 1 and the green figure have the same sizeThis means that the triangle that is a reflection of the green triangle is figure 1
Read more about transformation at
brainly.com/question/4289712
#SPJ1
A marble is selected from a bag containing eight marbles numbered 1 to 8. The number of the marble selected will be recorded as the outcome. Consider the following events. Event A: The marble selected has an even number.
Event B: The marble selected has a number from 3 to 6.
a) Event "A or B":
b) Event "A and B":
c) The complement of the event A.
Answers
Even numbers: 2, 4, 6, 8
Numbers from 3 to 6: 3, 4, 5, 6
Combining these sets and removing duplicates, we have the following outcomes: 2, 3, 4, 5, 6, 8. So, event "A or B" includes these outcomes.
b) Event "A and B" refers to the marble selected having both an even number and a number from 3 to 6. To determine the outcomes that satisfy this event, we need to find the numbers that meet both conditions.
Numbers that are both even and from 3 to 6: 4, 6
Therefore, event "A and B" includes the outcome of either 4 or 6.
c) The complement of event A refers to outcomes that are not part of event A. Since event A represents the marble selected having an even number, the complement of event A would be the marble selected having an odd number.
Odd numbers: 1, 3, 5, 7
Therefore, the complement of event A includes these outcomes.
A) - Event "A or B" Consists of the Outcomes:
{2, 3, 4, 5, 6, 8}
B) - Event "A or "B" Consists of the Outcomes:
{4, 6}
C) - The "COMPLEMENT of EVENT "A" Consists of the Outcomes:
{1, 3, 5, 7}
Step-by-step explanation:MAKE A PLAN:
List The OUTCOMES for EACH EVENT and their COMBINATIONS:
SOLVE THE PROBLEM:a) - EVENT "A": {2, 4, 6, 8}
EVENT "B": {3, 4, 5, 6}
EVENT "A" or "B": {2, 3, 4, 5, 6, 8}
b) - EVENT "A" or "B": {4, 6}
c) - The COMPLEMENT of the EVENT "A": {1, 3, 5, 7}
Draw the conclusion:A) - Event "A or B" Consists of the Outcomes:
{2, 3, 4, 5, 6, 8}
B) - Event "A or "B" Consists of the Outcomes:
{4, 6}
C) - The "COMPLEMENT of EVENT "A" Consists of the Outcomes:
{1, 3, 5, 7}
I hope this helps!
Use the disk method or the shell method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about each given line. y=6/x^2 ,y=0,x=1,x=3 .
1) Find the y-axis
2) Find the line y=6
Answers
Answer:
1) V = 12 π ㏑ 3
2) \(\mathbf{V = \dfrac{328 \pi}{9}}\)
Step-by-step explanation:
Given that:
the graphs of the equations about each given line is:
\(y = \dfrac{6}{x^2}, y =0 , x=1 , x=3\)
Using Shell method to determine the required volume,
where;
shell radius = x; &
height of the shell = \(\dfrac{6}{x^2}\)
∴
Volume V = \(\int ^b_{x-1} \ 2 \pi ( x) ( \dfrac{6}{x^2}) \ dx\)
\(V = \int ^3_{x-1} \ 2 \pi ( x) ( \dfrac{6}{x^2}) \ dx\)
\(V = 12 \pi \int ^3_{x-1} \dfrac{1}{x} \ dx\)
\(V = 12 \pi ( In \ x ) ^3_{x-1}\)
V = 12 π ( ㏑ 3 - ㏑ 1)
V = 12 π ( ㏑ 3 - 0)
V = 12 π ㏑ 3
2) Find the line y=6
Using the disk method here;
where,
Inner radius \(r(x) = 6 - \dfrac{6}{x^2}\)
outer radius R(x) = 6
Thus, the volume of the solid is as follows:
\(V = \int ^3_{x-1} \begin {bmatrix} \pi (6)^2 - \pi ( 6 - \dfrac{6}{x^2})^2 \end {bmatrix} \ dx\)
\(V = \pi (6)^2 \int ^3_{x-1} \begin {bmatrix} 1 - \pi ( 1 - \dfrac{1}{x^2})^2 \end {bmatrix} \ dx\)
\(V = 36 \pi \int ^3_{x-1} \begin {bmatrix} 1 - ( 1 + \dfrac{1}{x^4}- \dfrac{2}{x^2}) \end {bmatrix} \ dx\)
\(V = 36 \pi \int ^3_{x-1} \begin {bmatrix} - \dfrac{1}{x^4}+ \dfrac{2}{x^2} \end {bmatrix} \ dx\)
\(V = 36 \pi \int ^3_{x-1} \begin {bmatrix} {-x^{-4}}+ 2x^{-2} \end {bmatrix} \ dx\)
Recall that:
\(\int x^n dx = \dfrac{x^n +1}{n+1}\)
Then:
\(V = 36 \pi ( -\dfrac{x^{-3}}{-3}+ \dfrac{2x^{-1}}{-1})^3_{x-1}\)
\(V = 36 \pi ( \dfrac{1}{3x^3}- \dfrac{2}{x})^3_{x-1}\)
\(V = 36 \pi \begin {bmatrix} ( \dfrac{1}{3(3)^3}- \dfrac{2}{3}) - ( \dfrac{1}{3(1)^3}- \dfrac{2}{1}) \end {bmatrix}\)
\(V = 36 \pi (\dfrac{82}{81})\)
\(\mathbf{V = \dfrac{328 \pi}{9}}\)
The graph of equation for 1 and 2 is also attached in the file below.


a,b)Find the phasor form of the following E-field, the polarization type, and plot the vector on the X-y axis (z-0) for one period a) E(z,t) = xZcos(wt kz) y4cos(wt kz) b) E(z,t) = R2cos(wt + kz) - 94sin(wt + kz)
Answers
a) The phasor form of E-field = xˆ 2cos(wt - kz) - yˆ 4cos(wt - kz) is 2√5 L(-63.43).
Polarization type is linearly polarised.
b) The phasor form of E-field = ?
E(z,t) = xˆ 2cos(wt + kz) - yˆ 4sin(wt + kz) is E(z,t) =2√5 L(-143.43). polarization type is elliptical.
We have given that
E⃗(z,t) =2xˆcos(wt - kz) - 4 yˆcos(wt - kz)
|r⃗ | = √((2cos(wt - kz))² + (- 4cos(wt - kz))²)
= √(4cos²(wt - kz) + 16cos²(wt - kz))
= √(20cos²(wt - kz))
= 2√5 cos(wt - kz)
φ = 4cos(wt - kz)/(2cos(wt - kz))
= tan⁻¹ 1(-2) = -63.43°
So, E(z,t) = 2√5 L(-63.43)
b) E(z,t) = xˆ 2cos(wt + kz) - yˆ 4sin(wt + kz)
= xˆ 2cos(wt + kz) - yˆ 4cos(wt + kz -π/2)
|r| = √((2cos(wt + kz))² + (- 4sin(wt -+kz))²)
= √20
phi = tan⁻¹(- 4cos(wt - kz)/(2cos(wt - kz)) - π/2
= tan⁻¹( -2) + π/2 = - 143.43
so, E(z,t) =2√5 L(-143.43)
E(z,t) = xˆ 2cos(wt - kz) - yˆ 4cos(wt - kz)
if wt = 0°
E(z,t) = xˆ 2cos(0 - kz) - yˆ 4cos(0- kz)
= 2xˆ - 4yˆ
wt = 30° , E(z,t) = xˆ 2cos( - kz) - yˆ 4cos(0- kz)
E(z,t) = √3/2(2) xˆ - √3/2(4) yˆ
= √3xˆ - 2√3yˆ
for wt = 45°
E(z,t) = √2 xˆ - 2√2 yˆ
for wt = 90° =>E(z,t) = 0
for wt = 60° , E(z,t) = xˆ - 2 yˆ as seen in above graph that is linear polarised
For part (b) ,
E(z,t) = 2 xˆcos(wt - kz) - 4yˆ sin(wt + kz)
From graph elliptical polarised,
for wt = 0 , E(0,t) = 2 xˆ
for wt = 90° , E(0,t) = -4yˆ
for wt =180° , E(0,t) = -2 xˆ
for wt = 270° , E(0,t) = -4yˆ
Hence, we get the answer of both parts.
To learn more about E-field, polarization, refer:
https://brainly.com/question/3186980
#SPJ4
I don't really understand the question

Answers
Answer:
Angle bisector
Step-by-step explanation:
an angle bisector cuts an angle in half. COA goes from point c to point o to point a to make an angle. and OB is the exact middle of the angle. hope this helps :)
this leads us to a sturm-louiville problem in x. in each case the general solution in x is written with constants a and b
Answers
An example of a boundary value problem is the Sturm-Liouville problem, which entails determining the eigenvalues and eigenfunctions of a differential equation that complies with specific boundary requirements.
The general formula for the Sturm-Liouville problem's solution in x is y(x) = a * f(x) + b * g(x), where a and b are constants and f(x) and g(x) are the differential equation's eigenfunctions. When the differential equation and boundary conditions are solved, the eigenvalues and eigenfunctions are discovered.
For instance, if the differential equation has the following form: -y" + q(x)y = lambda* w(x)y where y is the dependent variable, y" is the second derivative of y, q(x) and w(x) are functions of x, and lambda is the eigenvalue, the boundary conditions can be of the following
form: where L is the length of the interval on which the differential equation is defined, y(0) = 0, and y(L) = 0.
The general solution in x can be expressed in the form: y(x) = a * f(x) + b * g(x), where a and b are constants and f(x) and g(x) are the eigenfunctions of the differential equation. The eigenvalues and eigenfunctions can be discovered by solving this differential equation and the boundary conditions.
For more information on sturm-louiville problem kindly visit to
https://brainly.com/question/4167035
#SPJ4
Andy is 5 feet tall. He casts a shadow of that is 9 feet long at the same time that a light post casts a shadow that is 35 feet long. What is the height of the light post? Sfeel 9 Teet 35 feet 1.3 ft 63 ft 19.4 ft 48 ft
Answers
First, we are going to draw a picture for the problem
We can formulate the following equation, given that we can use triangle similarity theorem.
\(\frac{\text{Andy height}}{x\text{ (post height)}}=\frac{\text{shadow of Andy}}{\text{Shadow of the post}}\)Replacing the values we have
\(\begin{gathered} \frac{5}{x}\text{ = }\frac{9}{35} \\ 5\cdot\frac{35}{9}=x \\ 19.4\text{ = x} \end{gathered}\)Isolating x, we get x is equal to 19.4 ft, which is the height of the post.

Whats the answer we need help?its been along time since i did this

Answers
Answer:
Try either 33.6 or 24
Step-by-step explanation:
I'm not really sure but it's either one of these two. Good luck
Explain your answer !!
Have a nice day
Will give braisnlt

Answers
Answer:
Equations:
\(4H + 3P = 13.75\)
\(2H + 5P = 11.25\)
\(H = 2.50\) --- Hot dog
\(P = 1.25\) --- Pretzel
Step-by-step explanation:
Represent hot dogs with H and Pretzels with P.
For Tina:
\(4H + 3P = 13.75\)
For Doug:
\(2H + 5P = 11.25\)
Solving for the price of both items:
We have:
\(4H + 3P = 13.75\) --- (1)
\(2H + 5P = 11.25\) --- (2)
Multiply (2) by 2
2 * (\(2H + 5P = 11.25\))
-------------------
\(4H + 10P = 22.50\) --- (3)
Subtract (3) from (1)
\(4H + 3P = 13.75\)
\(4H + 10P = 22.50\)
----------------------
\(4H - 4H + 3P - 10P = 13.75 - 22.50\)
\(3P - 10P = 13.75 - 22.50\)
\(-7P = -8.75\)
Solve for P
\(P = \frac{-8.75}{-7}\)
\(P = 1.25\)
Substitute 1.25 for P in (2)
\(2H + 5P = 11.25\)
\(2H + 5 * 1.25 = 11.25\)
\(2H + 6.25 = 11.25\)
Collect Like Terms
\(2H = 11.25-6.25\)
\(2H = 5\)
Solve for H
\(H = \frac{5}{2}\)
\(H = 2.50\)
Write equivalent fractions for 2 2/3 and 2 1/4 using a common denominator please hurry
Answers
The equivalent fractions for the mixed numbers, with the same denominator, are given as follows:
32/12 and 27/12.
How to obtain the equivalent fractions?The mixed numbers in the context of this problem are given as follows:
2 and 2/3.2 and 1/4.The fractions that represent each number are given as follows:
2 + 2/3 = 6/3 + 2/3 = 8/3.2 + 1/4 = 8/4 + 1/4 = 9/4.The least common factor of 3 and 4 is given as follows:
3 x 4 = 12.
Hence the equivalent fractions are given as follows:
12/3 x 8 = 32/12.12/4 x 9 = 27/12.More can be learned about equivalent fractions at https://brainly.com/question/17220365
#SPJ1
The driveway in front of the brown house is 35 feet long and the driveway in front of the red house is 7 yards, 9 feet long. Which house has the long driveway and by how much? *
Brown house driveway; larger by 30 feet
Red house driveway; larger by 7 feet
Brown house driveway; larger by 5 feet
They are both equal.
Answers
Answer:
Brown house driveway; larger by 5 feet
Step-by-step explanation:
Lets convert yds to ft
We know 3 ft = 1yd
3*7 = 21
so 7yds = 21 ft
Add the 9 ft
7yds 9ft = 21+9 = 30 ft
The house with the 35 ft driveway is longer by (35-30) or 5 ft
This equation is an example of:


Answers
This is using the idea that if (a+b)(c+d+e), then it distributes to a(c+d+e)+b(c+d+e).
It might help to let y = c+d+e.
(a+b)(c+d+e) = (a+b)y
(a+b)(c+d+e) = y(a+b)
(a+b)(c+d+e) = y*a+y*b
(a+b)(c+d+e) = a*y + b*y
(a+b)(c+d+e) = a*(c+d+e) + b*(c+d+e)
explain 3 factors that should be considered in the construction of index numbers
Answers
1. selection of index number: during the construction of index number it is to be kept in mind that the selection of the index number should be correct accordingly.
2. selection of formula: while the construction of index numbers it is compulsory to select the correct formula for the given question.
3. selection of price: selection of prices should be done accordingly while constructing the index numbers.`
construction of index number is also available in two parts:
1. simple
2. weighted
1. simple: the simple method is classified into simple aggregative and simple relative.
2. weighted: the weighted method is classified into a weighted aggregative and weighted average.
read more about the construction of numbers at:
https://brainly.in/question/55819681
Three times a number decreased by eighteen.
Answers
Answer:
3n-18
Step-by-step explanation:
let n be the number
n
3 times a number
3n
decreased by is subtraction
3n-18
Skyler is out shopping and sees that striped shirts are on sale for
$19.00 each, and plaid pants are on sale for $19.50 each. He
buys 8 shirts and 6 pairs of pants. What is the total of his
purchase?
The total was $_______
Answers
Answer:
His total is $269
Step-by-step explanation:
8x19 = 152
6x19.50 = 117
152+117 = 269
This Venn diagram shows sports played by 10 students.
Karl
Jada
Gabby
PLAYS
BASKETBALL
O A=0.50
OB. 0.29
OC. =0.40
D.
=0.20
Fran
Juan
lan
Ella
Let event A = The student plays basketball.
Let event B = The student plays soccer.
What is P(AB)?
PLAYS
SOCCER
Mickey
Mai
Marcus
Answers
The conditional probability for this problem is given as follows:
C. P(A|B) = 2/5 = 0.4 = 40%.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
For this problem, we have that 5 students play soccer, and of those, 2 play basketball, hence the conditional probability is given as follows:
C. P(A|B) = 2/5 = 0.4 = 40%.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

WILL GIVE 5 STARS
Angela plays soccer and golf for a total of 125 minutes every day. She plays soccer 45 minutes more than she plays golf.
Part A: Write a pair of linear equations to show the relationship between the number of minutes Angela plays soccer (x) and the number of minutes she plays golf (y) every day. (5 points)
Part B: How much time does Angela spend playing golf every day? (3 points)
Part C: Is it possible for Angela to have spent 80 minutes playing soccer every day? Explain your reasoning.
Answers
A: The linear equations are x + y = 125 and x = y + 45.
B: Everyday Angela spends 40 minutes in playing golf.
C: No, it is not possible for Angela to spend 80 minutes playing soccer every day.
What is a linear equation?
A linear equation is one that has a degree of 1 as its maximum value. No variable in a linear equation, thus, has an exponent greater than 1. A linear equation's graph will always be a straight line.
Part A:
Let x be the number of minutes Angela plays soccer every day
Let y be the number of minutes Angela plays golf every day
According to the problem statement the linear equations are -
x + y = 125 (total time playing both sports is 125 minutes)
x = y + 45 (Angela plays 45 more minutes of soccer than golf)
Part B:
Substitute x = y + 45 into the first equation -
(y + 45) + y = 125
Use the addition operation -
2y + 45 = 125
2y = 80
y = 40
Angela spends 40 minutes playing golf every day.
Part C:
If Angela spends 80 minutes playing soccer every day, then
x = 80
y + 45 = 80 (using the equation x = y + 45)
y = 35
But this would mean that she plays golf for 35 minutes and soccer for 80 minutes, which adds up to a total of 115 minutes.
This is not possible since the problem states that Angela plays both sports for a total of 125 minutes every day.
Therefore, it is not possible for Angela to have spent 80 minutes playing soccer every day.
To learn more about linear equation from the given link
https://brainly.com/question/2226590
#SPJ1
a) In GeoGebra Links to an external site., construct a triangle (e.g. ABC), find the measure of all angles and all sides. Identify the type of your triangle (acute, right, obtuse/ scalene, isosceles, equilateral). Then construct a quadrilateral (e.g. DEFG), measure all angles and all sides. Identify the type of your quadrilateral (irregular, square, rectangle, etc.) Use the text command available in GeoGebra to describe the type.
b) Make a screenshot of your work in Geogebra and insert in the space provided below.
Answers
All angles are 90 degrees.Rhombus: All sides are of equal length.Square: All angles are 90 degrees and all sides are of equal length
a) To construct a triangle in GeoGebra, we can follow the steps below:
Step 1: Open GeoGebra and select the ‘Polygon’ tool.
Step 2: Select the ‘Triangle’ option.
Step 3: Click three points anywhere on the graph.
Step 4: Once you have drawn the triangle, you can use the ‘Angle’ tool to measure all the angles in the triangle. Similarly, use the ‘Length’ tool to measure the length of each side of the triangle.To identify the type of triangle, we can use the following properties:Acute Triangle: All angles of the triangle are less than 90 degrees.Right Triangle: One of the angles in the triangle is 90 degrees.Obtuse Triangle: One of the angles of the triangle is greater than 90 degrees.Scalene Triangle: All sides of the triangle are of different lengths.Isosceles Triangle: Two sides of the triangle are of the same length.Equilateral Triangle: All sides of the triangle are of the same length.To construct a quadrilateral in GeoGebra, we can follow the steps below:
Step 1: Open GeoGebra and select the ‘Polygon’ tool.
Step 2: Select the ‘Quadrilateral’ option.
Step 3: Click four points anywhere on the graph.
Step 4: Once you have drawn the quadrilateral, you can use the ‘Angle’ tool to measure all the angles in the quadrilateral. Similarly, use the ‘Length’ tool to measure the length of each side of the quadrilateral.To identify the type of quadrilateral, we can use the following properties:Irregular Quadrilateral: All sides and angles of the quadrilateral are of different lengths and measures.Trapezium: Only one pair of opposite sides is parallel.Parallelogram: Opposite sides are parallel.Rectangle:.b) Since we need to add a screenshot of the work done in GeoGebra, we cannot add it here. However, while you construct the triangle and the quadrilateral, you can keep adding the measure of angles and sides to find the properties of the figure. You can then use the Text command available in GeoGebra to describe the type of triangle or quadrilateral that you have constructed. To use the Text command in GeoGebra, follow the steps below:
Step 1: Select the ‘Text’ tool from the toolbar
.Step 2: Click anywhere on the graph to add the text box.
Step 3: Type the text in the text box.
Step 4: Customize the font, color, and size of the text as required.
for more search question length
https://brainly.com/question/28322552
#SPJ8
-28< -7n solving one step inequalities
Answers
Answer:
-4 < n
Step-by-step explanation:
Answer:
4>n
Step-by-step explanation:
The sign flips because it is being divided by a negative number and -28 divided by -7 is +4. A neg/neg = positive.
Points A and B are on opposite sides of a lake. Another point, C. is 94.4 meters from Angle A. The measure of Angle A is 72° and the measure of Angle C is 30°. Find the distance between A and B.
Answers
To find the distance between points A and B, we can use trigonometry and the given information.
Let's label the distance between A and B as "d". We know that point C is 94.4 meters away from point A. From angle A, we have the measure of 72°, and from angle C, we have the measure of 30°.
Using trigonometry, we can use the tangent function to find the value of "d".
tan(72°) = d / 94.4
To solve for "d", we can rearrange the equation:
d = tan(72°) * 94.4
Using a calculator, we can evaluate the expression:
d ≈ 4.345 * 94.4
d ≈ 408.932
Therefore, the distance between points A and B is approximately 408.932 meters.
500 - 20x ≥ 200 I need help
Answers
Answer:
x \(\leq\) 15
Step-by-step explanation:
NO LINKS!!
1. Is it possible for the sequence t(n) = 5·2ⁿ to have a term with the value of 200? If so, which term is it? If not, justify why not.
2. Is it possible for the function f(x) = 5·2ˣ to have an output of 200? If so, what input gives this output? If not, justify why not.
Answers
Answer:
1) No,2) Yes, x ≈ 5.32-----------------------------
Part 1Given sequence:
t(n) = 5 · 2ⁿIf t(n) = 200, we can try to find the value of n:
5 · 2ⁿ = 2002ⁿ = 40There is no integer solution, since 32 < 40 < 64 or 2⁵ < 40 < 2⁶, the value of n should be between 5 and 6.
The sequence should include integer numbers, so there is no solution.
Part 2Given function:
f(x) = 5 · 2ˣSolve for x if f(x) is 200:
5 · 2ˣ = 2002ˣ = 40log 2ˣ = log 40x log 2 = log 40x = log 40 / log 2x = 5.32 (rounded)Answer:
1. No
\(\textsf{2.} \quad x=\dfrac{\ln 40}{\ln 2} \approx5.32\;(\sf 2\;d.p.)\)
Step-by-step explanation:
Question 1Given sequence:
\(t(n)=5 \cdot 2^n\)
To determine if the sequence has a term with a value of 200, substitute t(n)=200 into the equation and solve for n:
\(\implies 5 \cdot 2^n=200\)
\(\implies 2^n=40\)
\(\implies \ln 2^n=\ln 40\)
\(\implies n\ln 2=\ln 40\)
\(\implies n=\dfrac{\ln 40}{\ln 2}\)
\(\implies n=5.3219280...\)
In a sequence, n is a positive integer. Therefore, it is not possible for the sequence to have a term with the value of 200, as when t(n)=200, n is not a positive integer.
Question 2Given function:
\(f(x)=5 \cdot 2^x\)
To determine if the function has an output of 200, substitute f(x)=200 into the function and solve for x:
\(\implies 5 \cdot 2^x=200\)
\(\implies 2^x=40\)
\(\implies \ln 2^x=\ln 40\)
\(\implies x=\dfrac{\ln 40}{\ln 2}\)
\(\implies x=5.3219280...\)
Therefore, it is possible for the function to have an output of 200 when:
\(x=\dfrac{\ln 40}{\ln 2}\)
Kayla wants to find the width, AB, of a river. She walks along the edge of the river 100 ft and marks point C. Then she walks 22 ft further and marks point D. She turns 90° and walks until her location, point A, and point C are collinear. She marks point E at this location, as shown
Answers
Can u please help me with 3&4 I’m giving 20 point please help me

Answers
Answer:
Step-by-step explanation:

Keith tutors history. For each hour that he tutors, he earns 20 dollars. His earnings, E (in dollars), after tutoring for h hours is given by the following function.
E(h) = 20h
How much does Keith earn if he tutors for 4 hours?
Answers
hope this helps
Answer:
4 20x is 80 so he can earn 80 bucks in 4 hours
Step-by-step explanation:
<3
Which of the following sets of ordered pairs represents a function?
{(10,5), (10,-5), (5,10), (5,-10)}
{(10,5), (-10,-5), (5,10), (-5,-10)}
{(-6,-1), (13,8), (1,6), (1,-10)}
{(3,5), (-17,-5), (3,-5), (-17,5)}
Answers
The sets of ordered pairs that represents a function are {(10,5), (-10,-5), (5,10), (-5,-10)} and {(-6,-1), (13,8), (1,6), (1,-10)}
Ordered pair of a functionOrdered pairs are written as a coordinate (x, y). For the given x coordinate points to be a function, the value of its x coordinates (domain) must not be repeated.
From the given ordered pairs, {(10,5), (10,-5), (5,10), (5,-10)} and {(3,5), (-17,-5), (3,-5), (-17,5)} are not functions since there is repetition in their domains.
Hence the sets of ordered pairs that represents a function are {(10,5), (-10,-5), (5,10), (-5,-10)} and {(-6,-1), (13,8), (1,6), (1,-10)}
Learn more on functions here: https://brainly.com/question/6561461
#SPJ1
7. Find the area of the triangle using trigonometry.
Answers
The area of the triangle shown is 51.96 unit²
What is an equation?An equation is a expression that shows the relationship between numbers and variables.
The area of a triangle can be found given two adjacent sides and an angle between the two sides. It is given as:
Area = (1/2) * product of adjacent sides * sin(angle)
Hence:
Area of triangle shown = (1/2) * 10 * 12 * sin(60) = 51.96
The area is 51.96
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Owen and Genesis are making fruit salads for a picnic. Owen mixes 14 cups of melon
and 3 cups of apple and Genesis mixes 6 cups of melon and 1 cup of apple. Use Owen
and Genesis's percent of melon to determine whose fruit salad will taste more
melony.
Owen percent of melon (to nearest whole number):
=
Genesis percent of melon (to nearest whole number) =
o Owen's fruit salad will be more melony.
O Genesis's fruit salad will be more melony.
O The two fruit salads will be equally melony.
%
%
Answers
The person whose fruit salad will taste more melony is Genesis. The Option B is correct.
How can we calculate the percentage?A percentage is a value or ratio that may be stated as a fraction of 100. If we need to calculate a percentage of a number, we should divide it's entirety and then multiply it by 100.
We need to compute the melon percentage to determine whose fruit salad will taste more melony:
1. Ownen mixes 14 cups of melon and 3 cups of apple. The percentage for melon will be:
= 14/(3+14) × 100
= 82.3529411765
= 82.35%
2. Genesis mixes 6 cups of melon and 1 cups of apple. The percentage for melon will be:
= 6/7 × 100
= 85.7142857143
= 85.71%
Read more about percentages on:
brainly.com/question/24877689
#SPJ1
Explain the steps you would take to find a quotation of 1/3÷4/3
Answers
Answer:
Answer btw is 1/4 ;)
Step-by-step explanation:
First step in dividing fractions is to flip the second fraction, aka find the inverse.
\(\frac{1}{3}/\frac{4}{3} \\\frac{1}{3}*\frac{3}{4}\)
All you have to do from here is multiply.
\(\frac{3}{12}=\frac{1}{4}\)
Boom.