Four girls and six boys are in a Spanish club. Three of the people will be chosen at random to represent the group in a photograph. What is the probability that one girl and two boys will be chosen? 40% 50% 60% 70%
Answers
Answer:50 %
Step-by-step explanation:
Given
There are 4 girls and 6 boys in a club
Probability of choosing 1 girl and 2 boys is
\(=\dfrac{\text{No of ways of choosing 1 girl and 2 boys }}{\text{No of ways of choosing 3 member out of 10 member}}\)
No of ways of choosing 1 girl and 2 boys\(=^4C_1\times ^6C_2\)
\(P=\dfrac{^4C_1\times ^6C_2}{^{10}C_3}\)
\(P=\dfrac{4\times 15}{10\times 3\times 4}\)
\(P=\dfrac{15}{30}=\frac{1}{2}\)
i.e. \(50\%\)
The probability that one girl and two boys will be chosen from the Spanish club is 50%.
What is the probability?Probability is used to determine the odds that an event would happen. If the event would happen with certainty, it would have a value of 1. If it is certain the event would not happen, it would have a value of 0.
The probability = number of ways of choosing 1 girl and two boys / number of ways of choosing 3 people
(4x15) / (10 x 3 x 4) = 15/30 = 1/2 = 50%
To learn more about probability, please check: https://brainly.com/question/13234031
#SPJ2
Related Questions
What is the measure of angle 3 in degrees?
27 degrees
33 degrees
60 degrees
153 degrees

Answers
For the following pair of lines, identify the system by type.
consistent
inconsistent
equivalent
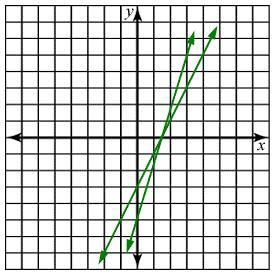
Answers
Considering that the two lines intersect at only one point, the system of equations described by them is consistent.
What is a system of equations?A system of equations is when two or more variables are related, and equations are built to find the values of each variable.
According to the number of solutions, the system is classified as follows:
Consistent: One solution.Equivalent: Infinite solutions.Inconsistent: No solutions.In this graph, each equation is described by a line, and they intersect once, meaning that there is one solution and the system is consistent.
More can be learned about a system of equations at https://brainly.com/question/24342899
#SPJ1
The puppy shelter where Riley works is moving to a new building. The rooms in the new building are built to hold 4 puppies each. Riley needs to figure out how many rooms she'll need to house a total of 72 puppies.
Use an equation to find the number of rooms Riley needs.
Answers
Riley needs 18 rooms for 72 puppies.
What is Division method?
Division method is used to distributing a group of things into equal parts.
Given that;
Riley works for puppy shelter moving to a new building.
The rooms in the new building are built to hold 4 puppies each.
Now, There are 1 room for 4 puppies.
Number of room for 4 puppies = 1
Hence, Number of room's for 72 puppies = 1/4 × 72
= 72/4
= 18
So, Riley needs 18 rooms for 72 puppies.
Learn more about the division method visit:
https://brainly.com/question/20066515
#SPJ1
If the mean of 9 score is 4.5 what must the 10th score be for the mean of all score to be 5
Answers
The 10th score should be 9.5 for the mean to be 5.
What is mean value ?The mean value is the average value of the given data.
According to the given question the mean of 9 score is 4.5 what must the 10th score be for the mean of all score to be 5.
The total average score for 9 games is
= ( 9 × 4.5 )
= 40.5.
The total average score for the mean to be 5 in 10 games is
= ( 10 × 5 )
= 50.
∴ The 10th score must be ( 50 - 40.5 ) which is
= 9.5.
learn more about mean here :
https://brainly.com/question/12513463
#SPJ4
a spherical balloon is inflated with gas at a rate of 500 cubic centimeters per minute. (a) how fast is the radius of the balloon changing at the instant the radius is 50 centimeters?
Answers
0.015 the radius of the balloon changing at the instant the radius is 50cm
given that
a spherical balloon is inflated with gas at a rate of 500 cubic centimeters per minute
radius = 50 centimeters
now we need to find the volume of the balloon
Let V = volume of the balloon at time t
r = radius of the balloon at time t
V = (4/3)πr3
Given: dV/dt = 500
Find: dr/dt when r = 50
dV/dt = (4/3)(3πr^2)(dr/dt)
500 = 4π(50)^2(dr/dt)
dr/dt = 1/(20π)
dr/dt = 0.015 cm/min
0.015 the radius of the balloon changing at the instant the radius is 50cm
To learn more about Volume:
https://brainly.com/question/1578538
#SPJ4
i dunno how to solve this!! {10th grd geometry}

Answers
the answer is 9.
ie.. the value of x =9

Area & Perimeter:
Determine the area and perimeter of the shape below.
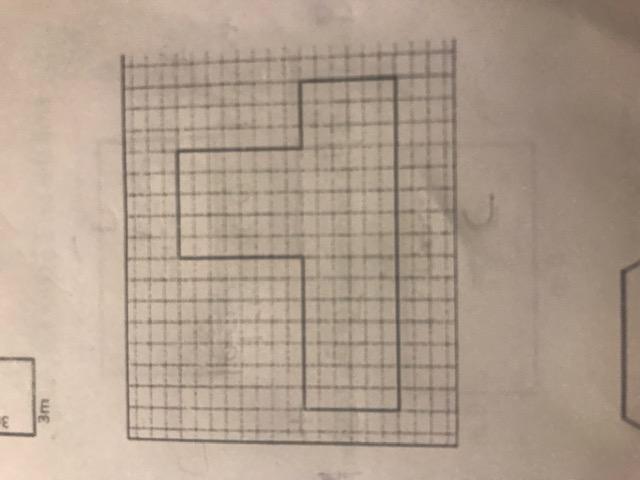
Answers
Solution 1: Count, which is crazy long so I am going to solution 2.
Solution 2: Calculate.
I am going to split the right part to the left part result two shapes: 8x5 and 6x15
8x5 + 6x15 = 40 + 90 = 130.
Area = 130 units^2
Perimeter: 8x2 + (6x2-5)+ (15x2-5) (Subtract 5 because the overlap area)
16 + 7 + 25 = 48
Perimeter = 48 units
The population of Mussman, Maine is 13,500 and grows at an annual rate of 6.5%. How long will it take the population of Mussman, Maine to reach 27,000 residents?
Please specify the steps
Answers
The year it will take Mussman to reach a population of 27,000 resident is 10.7 years
What is population growth?Population growth is the increase in the number of people in a population or dispersed group.
We use exponential function when calculating increase in population per time
p(t) =p(o) e^kt
27000 = 13500 e^0.065t
e^0.065t = 27000/13500
0.065t = ln 2
0.065t = 0.693
t = 0.693/0.065
t = 10.7 years
therefore it will take 10.7years for the resident of Mussman to reach a population of 27000
learn more about population growth from
https://brainly.com/question/1437549
#SPJ1
Find the quotient: 13 ÷ 5/11 pls help ASAP
Answers
Answer:
143/5
or
28 3/5
Step-by-step explanation:
ywwwwhshshd
Answer:
143/5, 28.6, or 28 3/5
How many feet per second is 1 mile/hour
Answers
Answer:
1.47 is the answer
Answer:
1.4666667 rounded off to 1.47
Step-by-step explanation:
You are solving a measurement problem where the numbers 2.09 × 109 and 4.053 × 10−4 are divided. how many significant digits should the quotient have? 4 3 2 1
Answers
The quotient of the division between 2.09 × 10^9 and 4.053 × 10^(-4) should have three significant digits.
When performing division, the general rule for determining the number of significant digits in the result is to consider the least number of significant digits in the original values being divided. In this case, the value 4.053 × 10^(-4) has three significant digits, while 2.09 × 10^9 has only two significant digits. Therefore, we should limit the quotient to the same number of significant digits as the divisor, which is three.
It's important to note that significant digits represent the reliable and meaningful digits in a measurement or calculation. By adhering to the rules of significant digits, we can maintain accuracy and convey the appropriate level of precision in our calculated results.
Learn more about quotient here
https://brainly.com/question/11418015
#SPJ11
2k=ak+7
Solve for k
Show your work
Answers
Answer:
k=a+7
Step-by-step explanation:
Take 1 k away from both sides. I hope you found this useful!
Answer:
k = \(\frac{7}{2-a}\)
Step-by-step explanation:
2k = ak + 7 ( subtract ak from both sides )
2k - ak = 7 ← factor out k from each term on the left side
k(2 - a) = 7 ( isolate k by dividing both sides by (2 - a) )
k = \(\frac{7}{2-a}\)
Suppose that a function f has derivatives of all orders at a. The the series ∑ k=0
[infinity]
k!
f (k)
(a)
(x−a) k
is called the Taylor series for f about a, where f(n) is the nth order derivative of f. Suppose that the Taylor series for 1−x
e x
about 0 is a 0
+a 1
x+a 2
x 2
+⋯+a 9
x 9
+⋯ Enter the exact values of a 0
and a 9
in the boxes below. a 0
=
a 9
=
因 송
Answers
Therefore, the values of \(a_0\) and \(a_9\) in the Taylor series expansion are: \(a_0 = 1; a_9 = 0.\)
To find the values in the Taylor series expansion of \((1 - x)/e^x\) about 0, we can use the formula for the coefficients of the Taylor series:
\(a_0 = f(0)/0!\\a_9 = f(9)/9!\)
Let's first find f(0):
\(f(0) = (1 - x)/e^x\)
Substituting x = 0:
\(f(0) = (1 - 0)/e^0\)
= 1/1
= 1
Next, let's find f(9):
f(9) = (9th derivative of (1 - x))/9!
To find the 9th derivative, we can repeatedly differentiate (1 - x) with respect to x:
f(x)=0--------------n time
Since all the higher-order derivatives are 0, the 9th derivative is also 0:
f(9) = 0
\(a_0 = f(0)/0!\)
= 1/1
= 1
\(a_9 = f(9)/9!\)
= 0/9!
= 0
To know more about Taylor series expansion,
https://brainly.com/question/32231446
#SPJ11
what influences does public health have on the U.S. health care system? what is a positive example and a negative example?
Answers
Public health has a crucial influence on the U.S. healthcare system by promoting disease prevention, health promotion, policy development, emergency preparedness, and more. Positive examples demonstrate how public health efforts improve health outcomes, reduce costs, and enhance population well-being. Negative examples highlight instances where shortcomings in public health can lead to health risks, increased healthcare burden, and adverse consequences for the population.
Public health plays a significant role in shaping the U.S. healthcare system. It encompasses a range of efforts and policies aimed at promoting and protecting the health of the population. Here are some influences of public health on the U.S. healthcare system:
Disease prevention and control: Public health initiatives focus on preventing the spread of infectious diseases, such as vaccination programs, disease surveillance, and outbreak investigations. These efforts help reduce the burden on the healthcare system by preventing illnesses and reducing healthcare costs.
Positive example: Successful vaccination campaigns have led to the eradication or significant reduction of diseases like polio and smallpox, protecting public health and reducing the need for costly treatments.
Negative example: Failure to adequately control and contain infectious diseases can lead to outbreaks and public health emergencies, straining healthcare resources and posing a risk to the population's health.
Health promotion and education: Public health agencies work to educate the public about healthy behaviors, lifestyle choices, and disease prevention strategies. They promote initiatives like smoking cessation programs, healthy eating campaigns, and physical activity promotion.
Positive example: Public health campaigns promoting smoking cessation have contributed to a decrease in smoking rates, resulting in improved public health outcomes and reduced healthcare costs associated with smoking-related diseases.
Negative example: Insufficient public health education and awareness campaigns on the dangers of substance abuse may contribute to increased addiction rates, leading to increased healthcare utilization and negative health outcomes.
Health policy and regulation: Public health agencies play a role in shaping health policies and regulations that govern the healthcare system. They develop and implement guidelines, standards, and regulations to ensure quality care, patient safety, and access to essential health services.
Positive example: Implementation of regulations mandating health insurance coverage for preventive services has increased access to preventive care, enabling early detection and treatment of diseases, and reducing healthcare costs in the long run.
Negative example: Inadequate regulation or enforcement of healthcare safety standards can lead to medical errors, hospital-acquired infections, and compromised patient safety.
Emergency preparedness and response: Public health agencies are responsible for preparing for and responding to public health emergencies, such as natural disasters, disease outbreaks, and bioterrorism events. They coordinate emergency response efforts, develop emergency plans, and ensure the availability of essential resources and healthcare infrastructure.
Positive example: Effective public health emergency preparedness and response during the H1N1 influenza pandemic in 2009 helped mitigate the impact of the virus, protecting public health and minimizing strain on the healthcare system.
Negative example: Inadequate preparedness or response to a public health emergency can lead to delayed or insufficient healthcare services, resulting in higher morbidity and mortality rates.
Learn more about public health have here, https://brainly.com/question/2051613
#SPJ11
Can you help me solve this!

Answers
Hello!
surface area
= 2(6*2) + 2(4*2) + 4*6
= 2*12 + 2*8 + 24
= 24 + 16 + 24
= 64 square inches
(b) what is the (approximate) probability that the sample mean hardness for a random sample of 35 pins is at least 51?
Answers
To solve this problem, we need to use the Central Limit Theorem, which states that the distribution of the sample means approaches a normal distribution as the sample size increases.
First, we need to find the mean and standard deviation of the sample mean hardness. The mean is simply the population mean, which is given as 50.5. The standard deviation of the sample mean is given by the formula:
standard deviation of sample mean = population standard deviation / sqrt(sample size)
The population standard deviation is given as 0.5, and the sample size is 35, so:
standard deviation of sample mean = 0.5 / sqrt(35) = 0.084
Next, we need to standardize the sample mean hardness using the z-score formula:
z = (sample mean hardness - population mean) / (standard deviation of sample mean)
z = (51 - 50.5) / 0.084 = 5.95
Finally, we need to find the probability that a standard normal distribution is greater than or equal to 5.95. This can be done using a z-table or a calculator. Using a calculator, we get:
P(Z ≥ 5.95) ≈ 0
Therefore, the approximate probability that the sample mean hardness for a random sample of 35 pins is at least 51 is very close to 0.
To learn more about mean : brainly.com/question/31101410
#SPJ11
find a formula for a function that has vertical asymptotes x = 2 and x = 4 and horizontal asymptote y = 2.
Answers
The function with the asymptotes as x = 2 , x = 4 and y = 2 is given by the relation f(x) = 2 / [(x - 2)(x - 4)]
Given data,
To find a function that has vertical asymptotes at x = 2 and x = 4, and a horizontal asymptote at y = 2, we can start by considering the basic form of a rational function:
f(x) = (ax + b) / (cx + d)
To satisfy the given conditions, we need the denominator of the rational function to have factors of (x - 2) and (x - 4) since these will create the vertical asymptotes at x = 2 and x = 4.
So, f(x) = (ax + b) / [(x - 2)(x - 4)]
Now, let's consider the horizontal asymptote at y = 2. For a rational function, the horizontal asymptote occurs when the degree of the numerator is less than or equal to the degree of the denominator. Since we want a horizontal asymptote at y = 2, which is a horizontal line, the numerator needs to be a constant, and the denominator needs to be linear.
Let's choose a = 0 and b = 2 so that the numerator is a constant equal to 2.
f(x) = 2 / [(x - 2)(x - 4)]
Hence , a formula for the function that satisfies the given conditions is given by f(x) = 2 / [(x - 2)(x - 4)].
To learn more about asymptotes click :
https://brainly.com/question/27871406
#SPJ12
The coordinates of the midpoint of GH are M (8,0) and the coordinates of one endpoint are H(-2, 9). The coordinates of the other endpoint are
Answers
Answer:
G(18,-9)
Step-by-step explanation:
The coordinates of the midpoint of GH are M (8,0) and the coordinates of one endpoint are H(-2, 9). We need to find the coordinates of G. Let G is (x,y).It can be done using mid point formula i.e. \((\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2})\)
So,
\(8=\dfrac{x-2}{2}\ \text{and}\ 0=\dfrac{9+y}{2}\\\\16=x-2\ \text{and}\ y=-9\\\\x=18\ \text{and}\ y=-9\)
Hence, the coordinates of the other point is (18,-9).
In inferential statistics, the objective is to determine how probable it is that:
The alternative hypothesis is true.
The null hypothesis is true.
The alternative hypothesis is false.
The null hypothesis is false.
Answers
In inferential statistics, the objective is to determine the probability of the alternative hypothesis being true or the null hypothesis being true.
This involves using sample data to make inferences and draw conclusions about a larger population. By analyzing the data and performing statistical tests, we assess the likelihood of the alternative hypothesis or the null hypothesis being accurate.
The alternative hypothesis represents a claim or statement that contradicts the null hypothesis and suggests that there is a significant relationship or difference between variables. To determine its probability, statistical methods such as hypothesis testing and p-values are employed. These methods evaluate the strength of evidence against the null hypothesis and support the alternative hypothesis when the evidence is substantial.
Know more about null hypothesis here:
https://brainly.com/question/28098932
#SPJ11
What is the slope of the line that passes through the points (7,9) and (15,-29)
Answers
Answer:
-4.75
Step-by-step explanation:
Slope = (y2-y1) / (x2-x1)
So applying the formula
(-29-9)/(15-7)
= -38/8 = -4.75
A line passes through the points (8,5) and (4,4). What is its equation im slope-intercept from?
Answers
Given the points ( 8 , 5 ) and ( 4 , 4 )
The general slop-intercept form of the equation of the line is:
y = mx + c
where m is the slope and c is y-intercept
The slope will be calculated as following:
\(\text{slope}=m=\frac{y2-y1}{x2-x1}=\frac{5-4}{8-4}=\frac{1}{4}\)So, the equation of the line will be:
\(y=\frac{1}{4}x+c\)Using the one of the given points to find the value of c
Let , we will use the point ( 4 , 4 )
so, when x = 4 , y = 4
\(\begin{gathered} 4=\frac{1}{4}\cdot4+c \\ 4=1+c \\ c=4-1=3 \end{gathered}\)So, the slope - intercept equation of the line is:
\(y=\frac{1}{4}x+3\)The population of rabbits on an island is growing exponentially. In the year 1990, the population of rabbits was 740, and by 1997 the population had grown to 870. Predict the population of rabbits in the year 2002, to the nearest whole number.
Answers
The population of the rabbit in the year 2002 will be 940 rabbits.
What is an expression?
Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Now,
The exponential model consisted the expression;
\(y = A r^{t}\)
Where, A is initial population and r is increase rate and t is time.
So, The initial population and increase rate for the given condition are;
\(740 = A . r^{0} \\\\A = 740\)
And,
\(870 = 740 * r^{7}\)
\(r^{7} = \frac{870}{740}\)
\(r^{7} = \frac{87}{74}\)
r = 1.89/1.84
r = 1.02
So, The exponential model consisted the expression;
\(y = A r^{t}\)
\(y = 740 r^{12}\)
\(y = 740 * (1.02)^1^2\)
\(y = 740 * 1.27\)
\(y = 939.8\)
Therefore,
The population of the rabbit in the year 2002 will be 940 rabbits.
Learn more about the exponential growth visit:
https://brainly.com/question/19961531
#SPJ1
PLEASE HELP ILL GIVE YOU BRAINLIEST

Answers
\(3x-y=17\\x+4y=10\) how can you tell that there is only one solution
Answers
The graph of a quadratic function goes through a vertex of (105, 27) and also (109, 14),
What is the value of “a” for this function?
Answers
Answer:
a = - \(\frac{13}{16}\)
Step-by-step explanation:
The equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is a multiplier
Here (h, k ) = (105, 27 ) , thus
y = a(x - 105)² + 27
To find a substitute (109, 14 ) into the equation
14 = a(109 - 105)² + 27 ( subtract 27 from both sides )
- 13 = 16a ( divide both sides by 16 )
a = - \(\frac{13}{16}\)
Suppose you park your car at a trailhead in a national park and begin a 2-hr hike to a lake at 7 A.M. on a Friday morning. On Sunday morning, you leave the lake at 7A.M. and start the 2-hr hike back to your car. Assume the lake is 3 mi from your car. Let f(t) be your distance from the car r hours after 7 A.M. on Friday morning and let g(t) be your distance from the car t hours after 7 A.M. on Sunday morning.
a. Evaluate f(0), f(2), g(0), and g(2).
b. Let h(t) = f(t) - g(t). Find h(0) and h(2).
c. Use the Intermediate Value Theorem to show that there is some point along the trail that you will pass at exactly the same time of morning on both days.
Answers
Answer:
The answer is given below
Step-by-step explanation:
The distance from the lake to the car is 3 miles and it takes 2 hours. The velocity of the hiker is 3/2 mi/hr. Therefore f(t) which is the distance from the car t hours after 7 A.M is given by:
\(f(t)=\frac{3}{2}t\)
When coming back on Sunday morning, the distance g(t) from the car at any point in time is given by:
\(g(t)=3-\frac{3}{2}t\)
a)
\(f(t)=\frac{3}{2}t\\f(0)=\frac{3}{2}(0)=0\ mile\\f(2)=\frac{3}{2}(2)=3\ miles\)
\(g(t)=3-\frac{3}{2}t\\g(0)=3-\frac{3}{2}(0)=3\ miles\\g(2)=3-\frac{3}{2}(2)=2-2=0\ mile\\\)
b)
\(h(t)=f(t)-g(t)=\frac{3}{2}t -(3-\frac{3}{2}t)=\frac{3}{2}t -3+\frac{3}{2}t=3t-3\\h(t)=3t-3\\h(0)=3(0)-3=0-3=-3\\h(2)=3(2)-3=6-3=3\)
c)
According to Intermediate Value Theorem, there exist a point b where f(b) = g(b). i.e. f(b) - g(b) = 0
\(h(b)=f(b)-g(b)=0\\h(0)=-3,h(2)=3\)
This means there exist a point b within the interval [-3, 3] where f(b) - g(b) = 0
Order these numbers from least to greatest.
2.1072, 2.37, 2.1, 2.307
Answers
find the volume of the region contained in the cylinder x 2 y 2 = 9, bounded above by the plane z = x and below by the xy-plane.
Answers
the volume of the region contained in the cylinder x² + y² = 9, bounded above by the plane z = x and below by the xy-plane is 0.
Given: The cylinder is x² + y² = 9, bounded above by the plane z = x and below by the xy-planeWe know that, the cylinder is x² + y² = 9Which is (x/a)² + (y/b)² = 1Where a = 3 and b = 3The plane is z = xThe region is bounded below by the xy-plane Thus, the volume of the region can be found by integrating z = x with limits of x² + y² ≤ 9.So, V = ∭ dx dy dz where the limits are given by the cylinder and the plane.V = ∫∫∫ (x) dV ... (1)Now, converting the integral into cylindrical coordinates we have,∫∫∫ (x) dV = ∫θ = 0 to 2π ∫r = 0 to 3 ∫z = 0 to r cos θ (r cos θ) rdzdrdθ ... (2)x = r cos θ, y = r sin θ, and z = z.We know that the limits of x² + y² ≤ 9 in cylindrical coordinates are 0 ≤ θ ≤ 2π, 0 ≤ r ≤ 3, 0 ≤ z ≤ r cos θ.Using (2) in (1), we haveV = ∫θ = 0 to 2π ∫r = 0 to 3 ∫z = 0 to r cos θ (r cos θ) rdzdrdθ= ∫θ = 0 to 2π ∫r = 0 to 3 [r² cos θ / 2] dr dθ= ∫θ = 0 to 2π [ 9 cos θ / 2 ] dθ= 9 [ sin θ ]θ = 0 to 2π= 0Thus, the volume of the region contained in the cylinder x² + y² = 9, bounded above by the plane z = x and below by the xy-plane is 0.
To know more about Volume of region Visit:
https://brainly.com/question/30785714
#SPJ11
Round 69581.491337 to the nearest thousand
Answers
Answer:
hope this helps:)
Step-by-step explanation:
the thousands place is right before the first comma therefore it is in bold here:
69581.491337
since 5 is \(\geq\) 5 you round 9 up to a 10
once you round, the numbers below it all turn into zeros.
giving the number to be 70,000
hope this helps:)
Answer: Heyaa!~
Your Answer Is... 70,000
Step-by-step explanation:
Hopefully this helps you!~
when you round the numbers below it all turn into zeros.It is believed that the world's current oil reserves total approximately 2000 billion barrels. If, on average, the total is decreasing by about 25 billion barrels of oil each year: a. Find a linear equation for the remaining oil reserves, R, in terms of t, the number of years beyond the present. b. Ten years from now, how much oil will be in the reserves? c. If the rate of depletion remains constant, when will the world's oil reserves be depleted?
Answers
- Linear equation for the remaining oil reserves R = -25t + 2000.
- Ten years from now, there will be 1750 billion barrels of oil in the reserves.
- If the rate of depletion remains constant, the world's oil reserves will be depleted in approximately 80 years from the present.
A. To find a linear equation for the remaining oil reserves:
Slope-intercept form of a linear equation: y = mx + b
Where y represents the remaining oil reserves (R),
x represents the number of years beyond the present (t),
m represents the slope, and
b represents the y-intercept.
The total oil reserves are decreasing by 25 billion barrels each year, we can determine the slope (m) as -25 billion barrels/year. Since, it is started with 2000 billion barrels initially (at t = 0), the y-intercept (b) is 2000 billion barrels.
Therefore, the linear equation for the remaining oil reserves (R) in terms of the number of years beyond the present (t) is:
R = -25t + 2000
B. To find how much oil will be in the reserves ten years from now (t = 10):
R = -25(10) + 2000
R = -250 + 2000
R = 1750 billion barrels
Therefore, ten years from now, there will be 1750 billion barrels of oil in the reserves.
c. To determine when the world's oil reserves will be depleted:
0 = -25t + 2000
25t = 2000
t = 2000/25
t = 80
Therefore, if the rate of depletion remains constant, the world's oil reserves will be depleted in approximately 80 years from the present.
To learn more about Linear equation:
https://brainly.com/question/32634451
#SPJ4