For the given hypothesis test, determine the probability of a Type II error or the power, as specified. A hypothesis test is to be performed to determine whether the mean waiting time during peak hours for customers in a grocery store has increased from the previous mean waiting time of 8.3 minutes. Preliminary data analyses indicate that it is reasonable to apply a -test. The hypotheses are H 0: μ = 8.3 H1: >8.3 The population standard deviation is 3.8 minutes. The sample size is 50. The significance level is 0.05. Find the probability of a Type II error if in fact the mean waiting timeu, is 9.8 minutes. A. 0.125 B. 0.05 C. 0.875 D. 0.95
Answers
Answer:
the probability of a Type II error if in fact the mean waiting time u, is 9.8 minutes is 0.1251
Option A) is the correct answer.
Step-by-step explanation:
Given the data in the question;
we know that a type 11 error occur when a null hypothesis is false and we fail to reject it.
as in it in the question;
obtained mean is 9.8 which is obviously not equal to 8.3
But still we fail to reject the null hypothesis says mean is 8.3
Hence we have to find the probability of type 11 error
given that; it is right tailed and o.5, it corresponds to 1.645
so
z is equal to 1.645
z = (x-μ)/\(\frac{S}{\sqrt{n} }\)
where our standard deviation s = 3.8
sample size n = 50
mean μ = 8.3
we substitute
1.645 = (x - 8.3)/\(\frac{3.8}{\sqrt{50} }\)
1.645 = (x - 8.3) / 0.5374
0.884023 = x - 8.3
x = 0.884023 + 8.3
x = 9.18402
so, by general rule we will fail to reject the null hypothesis when we will get the z value less than 1.645
As we reject the null hypothesis for right tailed test when the obtained test statistics is greater than the critical value
so, we will fail to reject the null hypothesis as long as we get the sample mean less than 9.18402
Now, for mean 9.8 and standard deviation 3.8 and sample size 50
Z = (9.18402 - 9.8)/\(\frac{3.8}{\sqrt{50} }\)
Z = -0.61598 / 0.5374
Z = - 1.1462 ≈ - 1.15
from the z-score table;
P(z<-1.15) = 0.1251
Therefore, the probability of a Type II error if in fact the mean waiting time u, is 9.8 minutes is 0.1251
Option A) is the correct answer.
Related Questions
1. Global warming creates local problems. Projections forecast that even a moderate air temperature increase of only 1.8 °F could cause brook trout distributions to decrease dramatically. For example, such a temperature increase would take Washburn county's 19 ponds that support brook trout down to 10 ponds. What would be the percent decrease in the number of ponds that support brook trout?
Answers
The percent decrease in the number of ponds that support brook trout would be approximately 47.37%.
To calculate the percent decrease in the number of ponds that support brook trout, we need to determine the difference between the initial number of ponds and the final number of ponds, and then express that difference as a percentage of the initial number of ponds.
Initial number of ponds: 19
Final number of ponds: 10
To calculate the percent decrease, we can use the following formula:
Percent Decrease = (Difference / Initial Value) * 100
Let's apply this formula to the given data:
Difference = Initial number of ponds - Final number of ponds
Difference = 19 - 10
Difference = 9
Percent Decrease = (9 / 19) * 100
Now, let's calculate the percent decrease:
Percent Decrease = (9 / 19) * 100
Percent Decrease ≈ 47.37%
For such more question on number:
https://brainly.com/question/30752681
#SPJ8
number 5 if you help me on this I will give you everything and can you put an explanation so I can understand it to

Answers
Answer:
2
Explanation:
Given the expression
\(\frac{(2+6)^2}{4\cdot9-4}\)First evaluate the addition operation in bracket
\(\begin{gathered} \frac{8^2}{4\cdot9-4} \\ =\text{ }\frac{64}{4\cdot9-4} \end{gathered}\)Evaluate the product;
\(\begin{gathered} \frac{64}{36-4} \\ =\text{ }\frac{64}{32} \\ =\text{ 2} \end{gathered}\)Hence the result of the expression is 2
Fill in the table using this function rule.
y=-3x-3
X
-2
-1
0
1
y
0
0
0
X
Ś

Answers
Answer:
X | y
---------------
-2 | 3
-1 | 0
0 | -3
1 | -6
Mr Victor had 100 computes for sale. He sold w computers in the moming and (2w+3) computers in the afternoon. He had 7 computers left. How many computers did he sell in the morning?
Answers
Using an equation, the number of computers Mr. Victor sold in the morning is 30.
What is an equation?An equation is an algebraic statement that shows the equality or equivalence of two or more mathematical expressions.
Unlike mathematical expressions, equations include the equal symbol (=).
The number of computers Mr. Victor has for sale = 100
Let the number of computers sold in the morning = w
Let the number of computers sold in the afternoon = (2w+3)
Let the number of computers left = 7
Equation:The total number of computers, 100 = w + (2w+3) + 7
100 = 3w + 10
3w = 90
w = 30
Thus, since Mr. Victor sold w computers in the morning, w is equal to 30.
Learn more about equations at https://brainly.com/question/2972832.
#SPJ1
PLEASE HELP ASAP!!!!!!! ILL MAKE YOU THE BRAINLEST
Select the three numbers between 2/5 and 250%
0.25
11/4
0.9
2.5%
7/8
78%
Answers
Answer:11/4, 7/8, 78%
Step-by-step explanation:
Answer:
0.9 78% 7/8.I hoped I helped
Determine if the equation given in slope-intercept form represents the graph. If the equation is correct support your reasoning with why it is correct. If the equation is incorrect, give the correct slope-intercept form equation explaining how you determined it.

Answers
The equation given in slope-intercept form does not represent the graph because the y-intercept of the graph is equal to 4 while the y-intercept of the equation is equal to 5.
What is the slope-intercept form?In Mathematics, the slope-intercept form of a line can be calculated by using this linear equation:
y = mx + c
Where:
m represents the slope.c represents the y-intercept.x and y are the data points.What is y-intercept?In Mathematics, the y-intercept of any graph such as a linear function, generally occur at the point where the value of "x" is equal to zero (x = 0).
Based on the information provided regarding the equations and graphs, the y-intercept are as follows:
The y-intercept of y = 4x + 5 is equal to 5.The y-intercept of this graph with point (0, 4) is 4.Read more on y-intercept here: brainly.com/question/19576596
#SPJ1

simplify √([2m5z6]/[ xy])
Answers
The simplified form of √([2m5z6]/[xy]) is (√2m√5z√6) / (√x√y).
To simplify the expression √([2m5z6]/[xy]), we can break it down step by step:
Simplify the numerator:
√(2m5z6) = √(2) * √(m) * √(5) * √(z) * √(6)
= √2m√5z√6
Simplify the denominator:
√(xy) = √(x) * √(y)
Combine the numerator and denominator:
√([2m5z6]/[xy]) = (√2m√5z√6) / (√x√y)
Thus, the simplified form of √([2m5z6]/[xy]) is (√2m√5z√6) / (√x√y).
For such more questions on simplified form
https://brainly.com/question/28323654
#SPJ8
he following data are from an experiment designed to investigate the perception of corporate ethical values among individuals who are in marketing. Three groups are considered: management, research and advertising (higher scores indicate higher ethical values). Marketing Managers Marketing Research Advertising 8 7 10 7 7 11 6 6 10 7 6 9 8 7 10 6 6 10 Compute the values identified below (to 1 decimal, if necessary). Sum of Squares, Treatment Sum of Squares, Error Mean Squares, Treatment Mean Squares, Error Use
Answers
Answer:
Sum of Squares=50.5
Treatment Sum of Squares, 4.5
Error Mean Squares, 0.3
Treatment Mean Squares 0.9
Error Sum of Square = 3
Step-by-step explanation:
Given data
Observation A B C
1 8 7 10
2 7 7 11
3 6 6 10
4 7 6 9
5 8 7 10
6 6 6 10
A B C Row total (xr)
1 8 7 10 25
2 7 7 11 25
3 6 6 10 22
4 7 6 9 22
5 8 7 10 25
6 6 6 10 22
Col total (xc) 42 39 60 141
Using calculator for summarizing data
∑x²=1155 ⇒(A)
∑x²c/r=16(42²+39²+60²)
=1/6(1764+1521+3600)
=1/6(6885)
=1147.5⇒(B)
∑x²r/c=13(25²+25²+22²+22²+25²+22²)
=1/3(625+625+484+484+625+484)
=1/3(3327)
=1109⇒(C)
(∑x)²/n=(141)²/18
=19881/18
=1104.5⇒(D)
Sum of squares total
SST=∑x²-(∑x)²/n=(A)-(D)
=1155-1104.5
=50.5
Sum of squares between rows
SSR=∑x²r/c-(∑x)²/n=(C)-(D)
=1109-1104.5
=4.5
Sum of squares between columns
SSC=∑x²c/r-(∑x)²n=(B)-(D)
=1147.5-1104.5
=43
Sum of squares Error (residual)
SSE=SST-SSR-SSC
=50.5-4.5-43
=3
ANOVA table
Source Sums Degrees of Mean Squares
of Variation of Squares freedom F- value
SS DF MS
Between Treatments SSR=4.5 r-1=5 MSR=0.9 3
Between Blocks SSC=43 c-1=2 MS =21.5 71.6667
Error (residual) SSE=3 (r-1)(c-1)=10 MSE=0.3
Total SST=50.5 rc-1=17
what is -9/12 + 4/12=
Answers
Answer:
I think it would be -0.416 but I'm not real sure so make sure before using my answer! :3 Have a great day!
2.2 2.1.4 a Given that A and B are complementary angles and 7 cos A-3 = 0. Determine WITHOUT the use of a calculator, the value of: 7 cos B-3 tan A. (4)
Answers
A 10 cm thick grindstone is initially 200 cm in diameter, and it is wearing away at a rate of LaTeX: 50cm^3/hr. At what rate is it's diameter decreasing
Answers
Complete question is;
A 10 cm thick grindstone is initially 200 cm in diameter, and it is wearing away at a rate of 50 cm/hr. At what rate is its diameter decreasing?
Answer:
Diameter is decreasing at the rate of 5/(2πr) cm/hr
Step-by-step explanation:
We are told the stone is wearing away at a rate of 50 cm/hr. This means the volume is decreasing. Thus;
dV/dt = -50 cm/hr
Now, a grindstone is in the shape of a cylinder. Thus, volume of grindstone is;
V = πr²h
dV/dr = 2πrh
Now,to find the rate at which the diameter is decreasing, we'll write;
dr/dt = (dV/dt)/(dV/dr)
dr/dt = -50/(2πrh)
We are given;
Diameter = 200 cm
Radius; r = 200/2 = 100 cm
Thickness; h = 10 cm
Thus;
dr/dt = -50/(2π × r × 10)
dr/dt = -5/(2πr) cm/hr
The rate at which grindstone diameter decreases is \(-5/2\pi r \;{\rm cm/hr}\) and this can be determined by using the given data.
Given :
A 10 cm thick grindstone is initially 200 cm in diameter and it is wearing away at a rate of 50 \(\rm cm^3/hr\).
The following steps can be used in order to determine the rate at which grindstone diameter decreases:
Step 1 - According to the given data, the rate at which grindstone volume decreases is:
\(\dfrac{dV}{dt} = 50\;{\rm cm^3/hr}\) --- (1)
Step 2 - The formula of the volume of the cylinder (grindstone) is given below:
\(V = \pi r^2 h\)
Step 3 - Differentiate the above expression with respect to 'r'.
\(\dfrac{dV}{dr} = 2\pi r h\) --- (2)
Step 4 - So, using the expression (1) and (2) the rate at which grindstone diameter decreases is:
\(\dfrac{dr}{dt}=\dfrac{\frac{dV}{dt}}{\frac{dV}{dr}}\)
\(\dfrac{dr}{dt}=\dfrac{-50}{2\pi r \times 10}\\\)
\(\dfrac{dr}{dt} = -\dfrac{5}{2\pi r }\; {\rm cm/hr}\)
So, the rate at which grindstone diameter decreases is \(-5/2\pi r \;{\rm cm/hr}\).
For more information, refer to the link given below:
https://brainly.com/question/12748872
Select the correct answer. A circle with radius 5 and center A. The coordinates of the center of the circle are (-3, 12). What is the general form of the equation of the given circle with center A? A. x2 + y2 + 6x − 24y − 25 = 0 B. x2 + y2 − 6x + 24y + 128 = 0 C. x2 + y2 + 6x – 24y + 128 = 0 D. x2 + y2 + 6x − 24y + 148 = 0
Answers
you'll want to work with the center-radius form of a circle equation for this. the center formula is \((x - h)^2 + (y - k)^2 = r^2\), where \((h, k)\) is your center and r is your radius. plug in the information your circle gives you: \(A(-3, 12)\), \(\text{radius} = 5\)
\((x + 3)^2 + (y - 12)^2 = (5)^2\) ... simplify the right side
\((x + 3)^2 + (y - 12)^2 = 25\) ... from here, you need to foil both of your binomials to convert this to the "general form" that your answer choices are in.
\((x + 3)^2 = (x + 3)(x + 3) = x^2 + 6x + 9\)
\((y - 12)^2 = (y - 12)(y - 12) = y^2 - 24y + 144\)
\(x^2 + 6x + 9 + y^2 - 24y + 144 = 25\) ... combine like terms
\(x^2 + 6x + y^2 - 24y + 153 = 25\) ... subtract 25
\(x^2 + 6x + y^2- 24y + 128 = 0\) is your equation. reorder it so that it's from the highest degree to the lowest:
\(\boxed{\bold{x^2 + y^2 + 6x - 24y + 128 = 0}}\)
ASAP!!! Please help me solve

Answers
Answer: j(x) = (x-1)(x+2)
The x-1 part is because of the root x = 1
The root x = -2 leads to the factor x+2
e) A student spent 50 minutes doing her homework. She spent m minutes doing Geography. 2m minutes doing Mathematics and the remaining (m + 7) minutes studying History. How many minutes did she spend doing Mathematics?
Answers
Answer: 22 minutes
Step-by-step explanation: m + 2m + m + 7 = 4m + 7
4m + 7 = 50
4m = 44
m = 11
2m = 11 x 2 = 22 minutes
the sum of two number is twenty-six using x to represent the smaller of the two numbers, translate "the difference between five more then the larger number and twice the smaller number' into a variable expression. then simplify
Answers
"the difference between five more than the larger number and twice the smaller number' can be written as the expression 31 -3x.
What is expression?Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement. It's possible to multiply, divide, add, or subtract with this mathematical operation.
Given, the sum of two numbers is twenty-six the difference between five is more than the larger number and twice the smaller number' into a variable expression.
Since x represents the smaller of the two numbers,
Thus the larger number will be 26 - x
The expression asked above will be:
=> 5 + larger number - 2 * smaller number
=> 5 + 26 - x - 2 * x
=> 31 -3x
therefore, "the difference between five more than the larger number and twice the smaller number' can be written as the expression 31 -3x.
Learn more about expression here:
https://brainly.com/question/23246712
#SPJ1
HELP! Recursive and explicit growth problem

Answers
The populations, considering an exponential function, are given as follows:
P(1) = 19.2.P(2) = 23.04.P(12) = 142.66.What is an exponential function?An increasing exponential function is modeled according to the rule presented as follows:
\(A(t) = A(0)(1 + r)^t\)
In which the variables of the function are:
A(0) is the initial amount of the function.r is the growth rate of the function, as a decimal.In this problem, the parameters are given as follows:
A(0) = 16, r = 0.2.
Hence the function, written as P(t), is:
\(P(t) = 16(1.2)^t\)
The numeric values are found replacing the lone instance of t by the value at which we want to find the numeric value, hence:
P(1) = 16 x (1.2)¹ = 19.2.P(2) = 16 x (1.2)² = 23.04.P(12) = 16 x (1.2)¹² = 142.66.More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
NO LINKS!! Please help me with the Domain and Range part 4ii

Answers
Answer:
9) D: (-4, 4]; R: [-6, -4]
10) D: [-5, -5]; R: (-7, ∞)
Step-by-step explanation:
You want the domain and range of the relations shown on the given graphs.
DomainThe domain of a relation is the set of x-values for which it is defined. An open circle indicates that point is not included in either the domain or range.
RangeThe range of a relation is the set of y-values that the relation produces. An open circle indicates the y-value at that point is not in the range.
9)The graph has an open circle at x = -4 on the left, and a solid dot at x = 4 on the right. All of the x-values between these have corresponding y-values.
The domain is (-4, 4].
The bottom (minimum) of the curve lies on the line y = -6, so that is the lowest value in the range. The relation produces all y-values between -6 and -4. The solid dot at (4, -4) means -4 is included in the range.
The range is [-6, -4].
10)The vertical line at x=-5 means -5 is the only value in the domain.
The domain is [-5, -5].
The vertical line extends upward from an open circle at y = -7. The open circle means -7 is not part of the range.
The range is (-7, ∞).
Answer:
9) Domain: (-4, 4]
Range: [-6, -4]
10) Domain: [-5]
Range: (-7, ∞)
Step-by-step explanation:
Definitions
An open circle indicates the value is not included in the interval.
A closed circle indicates the value is included in the interval.
An arrow shows that the function continues indefinitely in that direction.
Interval notation
( or ) : Use parentheses to indicate that the endpoint is excluded.
[ or ] : Use square brackets to indicate that the endpoint is included.
Domain & Range
The domain is the set of all possible input values (x-values).
The range is the set of all possible output values (y-values).
Question 9From inspection of the graph, the minimum x-value is x = -4 and the maximum x-value is x = 4.
There is an open circle at endpoint (-4, -4). Therefore, x = -4 is not included in the domain.
There is an closed circle at endpoint (4, -4). Therefore, x = 4 is included in the domain.
Therefore, the domain of the relation is restricted: (-4, 4]
From inspection of the graph, the minimum y-value is y = -6 and the maximum y-value is y = -4.
This maximum value is included in the range since there is a closed circle at (4, -4).
Therefore, the range of the relation is restricted: [-6, -4]
Question 10From inspection of the graph, the line is a vertical line at x = -5.
Therefore, the domain of the relation is restricted to x = -5: [-5]
From inspection of the graph, the minimum y-value is x = -7.
This minimum value is not included in the range since there is an open circle at (-5, -7).
There is an arrow on the other endpoint of the line, indicating that the line continues indefinitely in that direction.
Therefore, the range of the relation is restricted: (-7, ∞)
¿38 es el 65% de qué número?
Answers
Answer:
\(\frac{760}{13}\)
¡Espero que esto ayude!
Perform the following
mathematical operation, and
report the answer to the
appropriate number of
significant figures.
16.2156 +0.014 = [ ? ]
Answers
The appropriate number of significant figure of the mathematical operation 16.2156 +0.014 is 16.230.
Significant figures:16.2156 is a 6 significant figures number0.014 is a 2 significant figures numberTherefore,
16.2156 + 0.014 = 16.2296
Therefore, let's round it up to 5 significant figures as follows;
16.2296 = 16.230.learn more on mathematical operation here: https://brainly.com/question/13055274?referrer=searchResults
what is the answer to 7y+4r=48
Answers
Answer:
Step-by-step explanation:
Y


Answer:
Answer for r
5
Answer for y
7
Hope it helps
Please help!!!!!!!!!!!!!!

Answers
Answer:
The answer is A.
Step-by-step explanation:
1 plus 2x (276-5y) + 69= A.
What is 413,598 rounded to the nearest thousand?
Answers
Answer:
414,000
Step-by-step explanation:
When rounding to the nearest thousand, you need to focus on the hundreds column. Because the unit is 5, you round up (5,6,7,8,9 determine rounding up). Therefore the 3 in the thousands column becomes a "4".
MAX POINTS
WILL GIVE BRANLIEST PLEASE HELP
h(x)=3/x-h +k
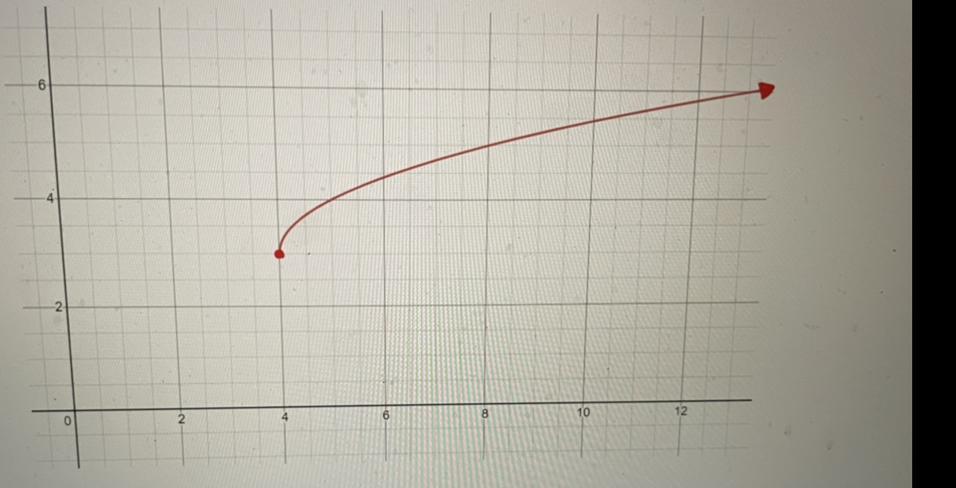
Oh no! He seems to be missing some parts though. He was "robbed" of his
asymptotes.
Luckily, he can remember what they were:
1. This functions vertical asymptote was x=-5.
2. This functions horizontal asymptote was y = 12.
Please recreate this function with those identifying features! Please make sure it
looks like the function in the picture
Answers
Let's do
\(\\ \rm\dashrightarrow y=\dfrac{3}{x-h}+k\)
Release k for some while
If
we take h=0So
y=3/xSo vertical asymptote is at origin now
It mentioned that it's at x=-5 so we need to change x
put -5 in place of h\(\\ \rm\dashrightarrow y=\dfrac{3}{x-(-5)}\)
\(\\ \rm\dashrightarrow y=\dfrac{3}{x+5}\)
Vertical asymptote at x=-5Now
for k=0 horizontal asymptote at originBut it's given
y is at 12Same put y=12 in place of k
\(\\ \rm\dashrightarrow y=\dfrac{3}{x+5}+12\)
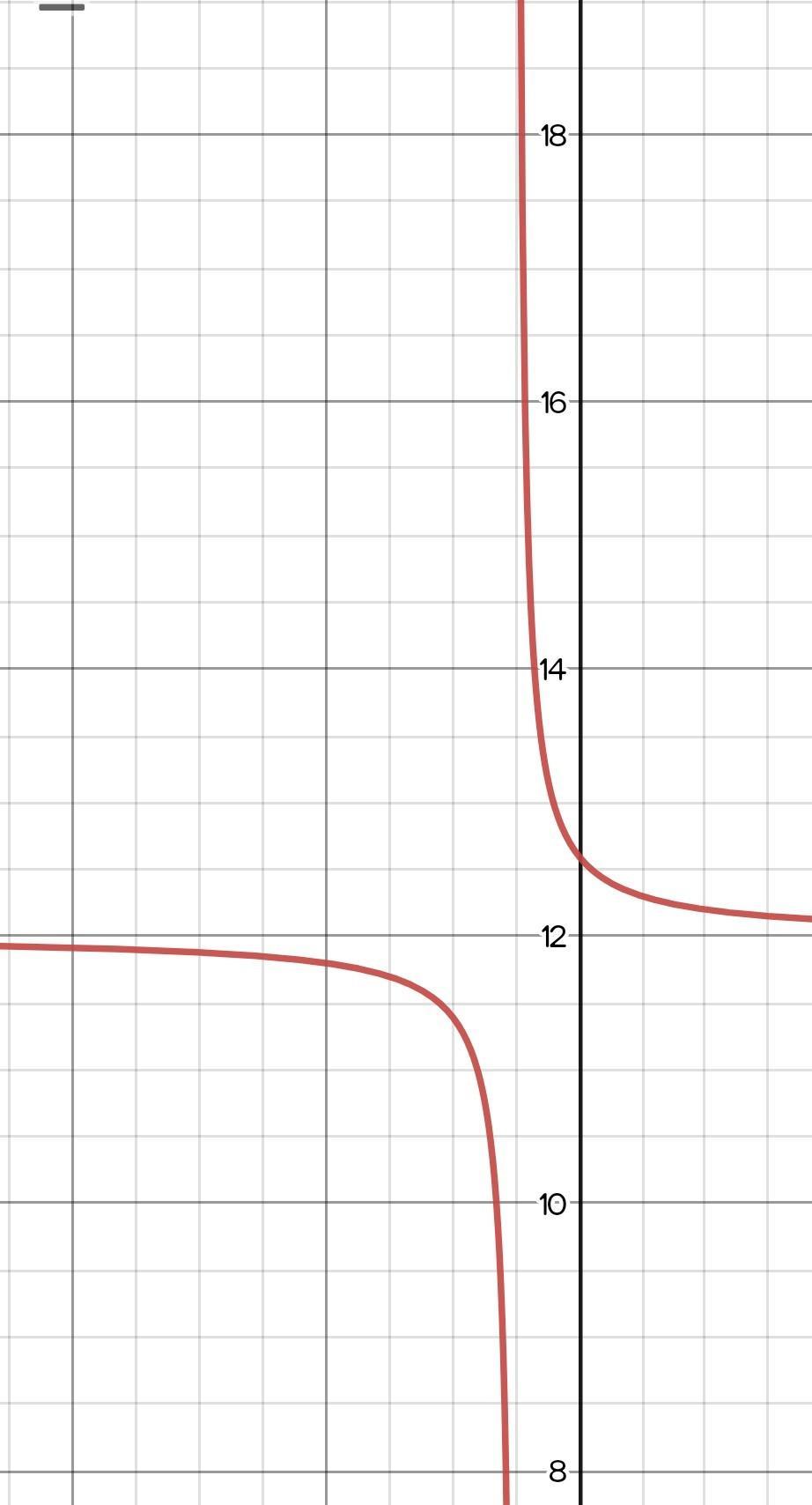
h=-5k=12Graph attached for verification
Answer:
h(x)=3/x+5 +12
Step-by-step explanation:
What is the volume of the box

Answers
Answer:
Volume = 144 in.³
Step-by-step explanation:
Given:
Length = 9 in.
Width = 4 in.
Height = 4 in.
Required:
Volume
Solution:
Volume of a box = length * height * width
Volume = 9*4*4
= 144 in.³
An elevator can hold at most 10 people and at most 1,200 pounds. Children weigh an average of 60 pounds each and adults weigh an average of 130 pounds each. If x is the number of children and y is the number of adults, which system of inequalities can be used to model all the allowable combinations of children and adults that can ride the
elevator?
a. x + y <_ 10
130x + 60y <_ 1200
b. x + y <_ 10
60x + 130y <_ 1200
c. 60x + 130y <_ 10
x + y <_ 1200
d. x - y _> 10
130x - 60y _> 1200
Answers
The answer would be x = 2 (children) and y = 8 (adults). Therefore, the maximum number of passengers that can ride the elevator is 2 children and 8 adults.
The correct system of inequalities to model all the allowable combinations of children and adults that can ride an elevator is a and b. We can calculate the total weight of the passengers in the elevator by multiplying the number of children by the average weight of a child (60 pounds) and the number of adults by the average weight of an adult (130 pounds). Therefore, the first inequality, x + y < 10, sets the limit on the number of people in the elevator, and the second inequality, 130x + 60y < 1200, sets the limit on the total weight that the elevator can hold. To solve for the allowable combinations of passengers, we can set up and solve a system of equations. For example, if we want to find the maximum number of adults and children that can ride the elevator, we can solve the equations x + y = 10 and 130x + 60y = 1200. The answer would be x = 2 (children) and y = 8 (adults). Therefore, the maximum number of passengers that can ride the elevator is 2 children and 8 adults.
Learn more about combination here:
https://brainly.com/question/20211959
#SPJ1
I will give brainiest to whoever answers correctly !!

Answers
Every week Roseanne gets paid $100 plus a 5% commission on all of her sales. If she has $5,000 in sales, how much is her pay for the week?
Answers
Answer:
$700 a 30%
Step-by-step explanation:
hope it help :)
Ahmed and Tiana buy a cake for $14 that is half chocolate and half vanilla. They cut the cake into 8 slices. If Ahmed likes chocolate four times as much as vanilla, what is the dollar value that Ahmed places on a chocolate slice?
Answers
The dollar value, if Ahmed likes 4 times more the chocolate than the vanilla slice, then he finds C four times more valuable than V. Thus, Ahmed placed a chocolate slice is $1.75.
What is meant by arithmetic?The foundational subject in mathematics, arithmetic covers operations with numbers. They include addition, subtraction, multiplication, and division. One of the major branches of mathematics, arithmetic serves as the cornerstone for students studying the subject of mathematics. Mathematical arithmetic is the study of the characteristics of the conventional operations on numbers.
Using C for the chocolate slice's value and V for the vanilla slice's value
4 slices × C + 4 slices × V = $14
If Ahmed likes 4 times more the chocolate than the vanilla slice, then he finds C four times more valuable than V, thus
C = 4×V
4 slices ×4V + 4 slices ×V = $24
20 slices ×P = $14
P=$0.7/slice
V= 4×P = 4×$0.7/slice = $2.8/slice
Thus for a slice that is half chocolate and half vanilla
value= 1/2 slice× C + 1/2 slice × V
= 1/2 slice ( $0.7 /slice + $2.8/slice)
= $1.75
Hence, Ahmed placed a chocolate slice is $1.75.
To learn more about arithmetic, visit:
https://brainly.com/question/29116011
#SPJ1
A distribution of values is normal with a mean of 60 and a standard deviation of 16. From this distribution, you are drawing samples of size 25. Find the interval containing the middle-most 76% of sample means.
Answers
Answer:
The interval containing the middle-most 76% of sample means is between 56.24 and 63.76.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
A distribution of values is normal with a mean of 60 and a standard deviation of 16.
This means that \(\mu = 60, \sigma = 16\)
Samples of size 25:
This means that \(n = 25, s = \frac{16}{\sqrt{25}} = 3.2\)
Find the interval containing the middle-most 76% of sample means.
Between the 50 - (76/2) = 12th percentile and the 50 + (76/2) = 88th percentile.
12th percentile:
X when Z has a p-value of 0.12, so X when Z = -1.175.
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(-1.175 = \frac{X - 60}{3.2}\)
\(X - 60 = -1.175*3.2\)
\(X = 56.24\)
88th percentile:
\(Z = \frac{X - \mu}{s}\)
\(1.175 = \frac{X - 60}{3.2}\)
\(X - 60 = 1.175*3.2\)
\(X = 63.76\)
The interval containing the middle-most 76% of sample means is between 56.24 and 63.76.
Dividing fractions word problems, please help I need it........

Answers
Answer:
25
Step-by-step explanation:
l x w = h
25 x 7.2 = 180
