For the given functions f and g, find the indicated valur4×=×2+6×,g(×=×+4(g • f)(2)
Answers
Given:
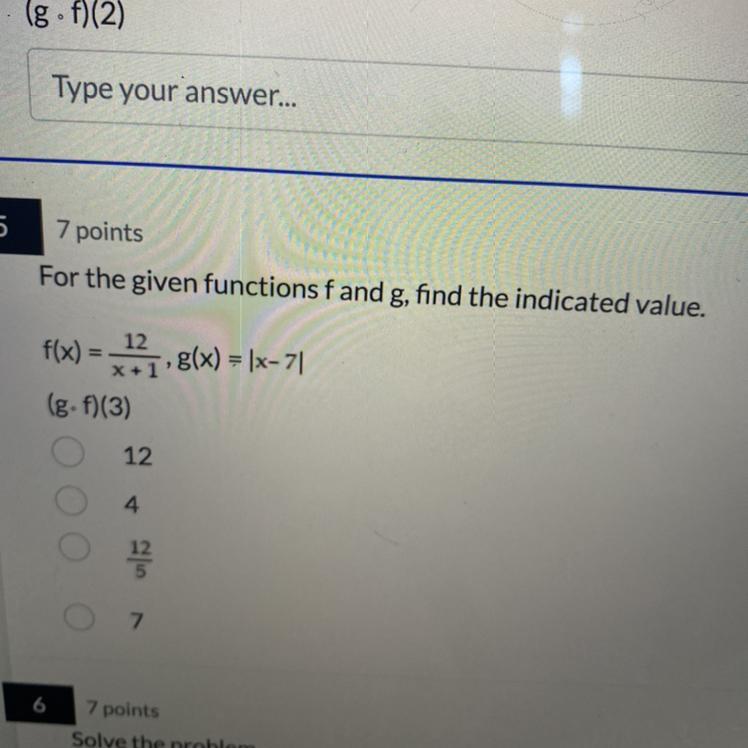
\(f(x)=\frac{12}{x+1\text{ }}\text{ and g\lparen x\rparen=}\lbrack x+7\rbrack\)Required:
\((g.f)(3)\)Explanation:
First of all we are going to place the value of function f(x) in g(x)
(gof)(3)=g(f(x))
=gof(3)=
\(\begin{gathered} \lbrack\frac{12}{3+1}-7\rbrack\text{ } \\ Now\text{ we are going to take lcm } \\ \lbrack\frac{12}{4}-7\rbrack \\ \lbrack3-7\rbrack \\ \lbrack-4\rbrack \\ 4 \end{gathered}\)Required answer:
option ii(4)
Related Questions
Divide. 4–3 43 4–4 44
Answers
Answer:
the answer is c on edge
Step-by-step explanation:
the second part is A-1/256
Answer:
C. \(4^{-4}\)
A. \(\frac{1}{156}\)
Step-by-step explanation:
edge 2021
Charlie the trainer has two solo workout plans that he offers his clients: Plan A and plan B. Each client does either one or the other (not both). On Wednesday there were 5 clients who did plan A and 6 who did plan B. On Thursday there were 3 clients who did plan A and 2 who did plan B. Charlie trained his Wednesday clients for a total of 7 hours and his Thursday clients for a total of 3 hours. How long does each of the workout plans last?
Answers
Plan A lasts for 0.5 hours, and Plan B lasts for 0.75 hours based on the given information and the solution to the System of equations.
To determine the duration of each workout plan, let's assume that both Plan A and Plan B have a fixed duration. Let's denote the duration of Plan A as "x" hours and the duration of Plan B as "y" hours.
From the given information, we can form the following equations:
On Wednesday:
5 clients did Plan A, so the total duration for Plan A is 5x hours.
6 clients did Plan B, so the total duration for Plan B is 6y hours.
The total training duration on Wednesday is 7 hours, so we have the equation: 5x + 6y = 7 ... Equation (1)
On Thursday:
3 clients did Plan A, so the total duration for Plan A is 3x hours.
2 clients did Plan B, so the total duration for Plan B is 2y hours.
The total training duration on Thursday is 3 hours, so we have the equation: 3x + 2y = 3 ... Equation (2)
We now have a system of equations (Equation 1 and Equation 2) that we can solve to find the values of x and y.
Multiplying Equation (1) by 2 and Equation (2) by 5 to eliminate the y variable, we get:
10x + 12y = 14 ... Equation (3)
15x + 10y = 15 ... Equation (4)
Multiplying Equation (3) by 3 and Equation (4) by 2 to create a new system of equations:
30x + 36y = 42 ... Equation (5)
30x + 20y = 30 ... Equation (6)
Subtracting Equation (6) from Equation (5), we can eliminate the x variable:
(30x + 36y) - (30x + 20y) = 42 - 30
16y = 12
y = 12/16
y = 0.75
Substituting the value of y into Equation (2), we can solve for x:
3x + 2(0.75) = 3
3x + 1.5 = 3
3x = 3 - 1.5
3x = 1.5
x = 1.5/3
x = 0.5
Therefore, the duration of Plan A is 0.5 hours, and the duration of Plan B is 0.75 hours.
Plan A lasts for 0.5 hours, and Plan B lasts for 0.75 hours based on the given information and the solution to the system of equations.
To know more about System .
https://brainly.com/question/13729904
#SPJ8
what is 9/16 simplyfied
Answers
Hope this Helps!
Solve for 2. Round to the nearest tenth, if necessary.
B
U
67
T
x
142°

Answers
Tan(angle) = opposite/ adjacent
tan(42) = 67/x
x =67/tan(42)
X = 74.411
rounded to nearest tenth : x = 74.4
Suppose that $7500 is placed in an account that pays 6% interest compounded each year.
Assume that no withdrawals are made from the account.
Follow the instructions below. Do not do any rounding.
(a) Find the amount in the account at the end of 1 year.
(b) Find the amount in the account at the end of 2 years
Answers
a) The compounded amount in the account at the end of 1 year is $7,950.
b) The compounded amount in the account at the end of 2 years is $8,427.
What is compound interest?Compound interest is the interest added to the principal amount after each period in order to compute the period's interest.
By compounding, we mean that accumulated interest is added to the principal to compute the subsequent interest.
Compound interest is unlike simple interest, which does not compound interest.
The compound interest formula is:
A = P(1 + r/n)^nt
A = Final amount
P = initial principal balance
r = interest rate
n = number of times interest is applied per time period
t = number of time periods elapsed
Since this investment is compounding annually, we can find the final amount at the end of each year using the common formula as follows:
A = P(1 + r)ⁿ
Principal = $7,500
Compound interest rate = 6%
Compounding period = Annually
Amount at the end of Year 1 = $7,950 ($7,500 x 1.06¹)
Amount at the end of Year 2 = $8,427 ($7,500 x 1.06²)
Thus, the compounded amount at the end of year 1 is $7,950 and $8,427 at the end of year 2.
Learn more about compound interest at https://brainly.com/question/24274034
#SPJ1
Solve the equation
2^2x+1 +5(2^x) -3=0
Please help
Answers
Answer:
The answer is -1
Step-by-step explanation:
2^(2x+1) = 2^2x × 2^1 = 2^2x × 2
after this we can make appointments
2^x = t
and then solve it :)

Please answer ASAP I will brainlist

Answers
Answer:
Step-by-step explanation:
(a) To find the linear cost function C(x), we need to consider the fixed cost and the marginal cost. The fixed cost is $100, and the marginal cost is $8 per pair of earrings.
The linear cost function can be represented as C(x) = mx + b, where m is the slope (marginal cost) and b is the y-intercept (fixed cost).
In this case, the slope (m) is $8, and the y-intercept (b) is $100. Therefore, the linear cost function is:
C(x) = 8x + 100.
(b) The average cost function (AC) can be found by dividing the total cost (C(x)) by the number of units produced (x):
AC(x) = C(x) / x.
Substituting the linear cost function C(x) = 8x + 100, we have:
AC(x) = (8x + 100) / x.
(c) To find C(5), we substitute x = 5 into the linear cost function:
C(5) = 8(5) + 100
= 40 + 100
= 140.
Interpretation: C(5) = 140 means that when the artist produces 5 pairs of earrings, the total cost (including fixed and variable costs) is $140.
(d) To find C(50), we substitute x = 50 into the linear cost function:
C(50) = 8(50) + 100
= 400 + 100
= 500.
Interpretation: C(50) = 500 means that when the artist produces 50 pairs of earrings, the total cost (including fixed and variable costs) is $500.
(e) The horizontal asymptote of C(x) represents the cost as the number of units produced becomes very large. In this case, the marginal cost is constant at $8 per pair of earrings, indicating that as the number of units produced increases, the cost per unit remains the same.
Therefore, the horizontal asymptote of C(x) is $8, indicating that the average cost per pair of earrings approaches $8 as the number of units produced increases indefinitely.
In practical terms, this means that for every additional pair of earrings produced beyond a certain point, the average cost will stabilize and remain around $8, regardless of the total number of earrings produced.
Write x-coordinate of the solution to then given 2x2 system in the space below. Write only the numeric answer. For example if the solution is x=3 write only 3 X+y=2 X-y=14
Answers
The most appropriate choice for simultaneous linear equation will be given by-
\(x = \frac{16}{5}\) is the required value of \(x\)
What is simultaneous linear equation?
Two or more linear equation having the same variables is known as simultaneous linear equation.
Simultaneous linear equation can be solved by elimination method, substitution method, cross multiplication method.
Here,
The system of equation is given by-
\(3x + y = 2\) ................ (1)
\(2x - y =14\) ................. (2)
Adding (1) and (2)
\(5x = 16\)
\(x = \frac{16}{5}\)
\(x = \frac{16}{5}\) is the \(x\) coordinate of the solution.
To learn more about simultaneous linear equation, refer to the link:
https://brainly.com/question/26310043
#SPJ10
Type the correct answer in each box. Use numerals instead of words.
What is the inverse of this function?
f(x=-½√x+3, x≥-3
f^-1(x)=__x²-__, for x ≤__
Answers
Answer:
read
Step-by-step explanation:
To find the inverse of the given function f(x) = -½√(x + 3), x ≥ -3, we can follow the steps for finding the inverse:
Step 1: Replace f(x) with y.
y = -½√(x + 3)
Step 2: Swap x and y.
x = -½√(y + 3)
Step 3: Solve for y.
Multiply both sides by -2:
-2x = √(y + 3)
Square both sides:
(-2x)^2 = (y + 3)
4x^2 = y + 3
Step 4: Replace y with f^(-1)(x).
f^(-1)(x) = 4x^2 - 3
Therefore, the inverse of the given function is:
f^(-1)(x) = 4x^2 - 3
However, it's worth noting that the domain of the inverse function may be restricted by the domain of the original function. Since the original function has a condition x ≥ -3, the inverse function's domain may be restricted as well.
Use the histogram to answer the following questions.
Frequency
The frequency of the class 90-93 is
The frequency of the class 94-97 is
This means that a total of
5.5
5
4.5
Your answers should be exact numerical values.
The frequency of the class 86-89 is
86
94
90
Duration of Dormancy (minutes)
dormancy periods were recorded.
Answers
The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of periods is given as follows:
5 + 6 + 4 = 15.
The frequency of each class is given as follows:
86 - 89: 5/15 = 1/3.90 - 93: 6/15 = 2/5.94 - 97: 4/15.Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

green foods purchases packages of noodles by the carton. each carton contains 36 packages and costs $43.20. green foods sells the noodles for $2.29 per package. what is the markup per carton?
Answers
Answer:
91% markup
Step-by-step explanation:
$43.20 divided by 36 is $1.20 per package
if Green Foods is selling one package for $2.29 then they are marking each package up by $1.19
if you take the difference of the per carton prices (82.44-43.20) and divide it by 43.20, you get a 91% markup
what is the volume of a cylinder with a diameter of 8 name m and a height of 5.5
Answers
To begin, you must plug all the values you have into a formula, and also putting them in the right form.
The formula for the volume of a cylinder is: πr²h
FINDING RADIUS: With this in mind, now we know that, our diameter must be converted to a radius. To do this, you divide your diameter by two. This gives you, 4 as your radius.
FINDING HEIGHT: In the question you sent, you can tell they've given you, your height, so all you need to do is plug it into the equation.
PLUGGING IT IN:
Your pi, stays the same when using a calculator, just press your pi symbol depending on the calculator you are using. Your radius is 4, therefore it wants you to square it, which is 4x4, which equals 16. Next, you want to multiply it by the height, so just multiply it with your height, 5.5
YOUR ANSWER:
276.46m
3. The customs duty on an imported vehide is 45% of imported price. (a) Calculate the customs duty опа car for which the imported price. is $3000 000. of a mini (6) Calculate the imported price bus if the amount paid induding customs duty TS $1560 000. ES
Answers
a) The customs duty on the car would be $1,350,000.
b) The imported price of the bus would be $858,000.
(a) To calculate the customs duty on a car with an imported price of $3,000,000, we can multiply the imported price by the duty rate of 45%:
Customs duty = $3,000,000 * 0.45 = $1,350,000.
(b) To calculate the imported price of a bus if the amount paid, including customs duty, is $1,560,000, we need to determine the portion of the total amount that represents the customs duty. Since the customs duty is 45% of the imported price, we can set up the following equation:
Customs duty = $1,560,000 * 0.45.
Solving for the customs duty:
Customs duty = $702,000.
Now, we can subtract the customs duty from the total amount to find the imported price:
Imported price = $1,560,000 - $702,000 = $858,000.
In summary, the customs duty on a car with an imported price of $3,000,000 would be $1,350,000. On the other hand, if the amount paid for a bus, including customs duty, is $1,560,000, the imported price of the bus would be $858,000.
for more such questions on equation
https://brainly.com/question/22688504
#SPJ8
i am a cube that has a lenght, width, and hight of 1 unit
Answers
Answer: The volume of the cube is 1.
Step-by-step explanation:
To find the volume for a cube, multiply all of the units for the sides together.
1 x 1 x 1 = 117. A man's shoe size is related to his foot length and can be modeled bythe equation s = 1.77 - 7.2, where s is shoe size and fis foot length, ininches. What is the shoe size of a man whose foot measures 9 inches?S? f=q5=1.7f=7.2A6В.8CD10N

Answers
s = shoe size
f = foot length
Therefore,
\(\begin{gathered} s=1.7f-7.2 \\ f=9\text{ inches} \\ s=1.7(9)-7.2 \\ s=15.3-7.2 \\ s=8.1\text{ inches} \end{gathered}\)In 2020, one of the states with the fewest people living in it is Wyoming, with a population of 585,501. Write the number that is ten thousand greater than 585,501
Answers
The number that is ten thousand greater than 585,501 is 595,501.
What is a greater number?A greater number is a number that when compared with another has a higher numerical value than the former.
To show that a number is greater than another, more values can be determined to account for their differences using basic mathematical operations like addition, subtraction, multiplication, and division.
Data and Calculations:The population of Wyoming in 2020 = 585,501
Additional population to Wyoming = 10,000
New population of Wyoming = 595,501 (585,501 + 10,000)
Thus, the number that is ten thousand greater than 585,501 is 595,501.
Learn more about the number system at https://brainly.com/question/17200227
#SPJ1
twenty six thousandths in numerical form
Answers
Answer:
0.026
Step-by-step explanation:
Twenty-Six = 26 ( But for simplicity in the Next Step write it as 26.)
Tenths means to move the Decimal Point 1 Place LeftHundredths means to move the Decimal Point 2 Place LeftThousandths means to move the Decimal Point 3 Place LeftThen Twenty-Six Thousandths = 0.026
Determine the number of triangular films that can be formed by using the measurements a = 17 cm,b = 23 cm, and m∠A = 40°. Solve each triangle. Round to the nearest tenth.
PLS HELP!!!!
Answers
The solution of the triangle have been shown below.
How do you solve the triangle?To solve a triangle means to find the values of all its angles and sides. The method for solving a triangle depends on the given information.
Given that;
a/Sin A = b/SinB
Sin B = bSin A/a
B = Sin-1(bSin A/a)
B = Sin-1 (23Sin 40/17)
B = 60.4 degrees
Then we have that
C = 180 - (40 + 60.4)
= 79.4 degrees
Then;
a/sinA = c/Sin C
c= aSin C/Sin A
c = 17 * Sin 79.4/Sin 40
c = 16.71/0.643
c = 25.9
Learn more about triangle:https://brainly.com/question/2773823
#SPJ1
A 30-ounce jar of salad dressing costs $2.39. A 24-ounce jar costs $2.14, and a 13-ounce jar costs $1.42. To the nearest cent, what is the cost per ounce of each size jar? Which one is the best buy?
Answers
Answer:
the 13 ounce one is best to buy
8 X 10-3 is how many times as great as 4X 10-6

Answers
Answer:
\(2X10^{3}\)
Step-by-step explanation:
Convert 50°F to degrees Celsius.
If necessary, round your answer to the nearest tenth of a degree.
Here are the formulas.
C=5/9(F-32)
F=9/5C+32

Answers
Answer:
10°C
Step-by-step explanation:
F = 50
C = 5/9 * (F - 32) = 5/9 * (50 - 32) = 5/9 * 18 = 5 * 2 = 10
Help 20 points (show your work)

Answers
The measure of angle ADC in the geometric system is equal to 55°.
How to determine the value of an angle related to a geometric system
In this question we find a geometric system formed by a quadrilateral and an angle vertical to a vertex of the quadrilateral. Angle CDE is supplementary to angles EDF and ADC. Two angles are supplementary whose sum of measures equals 180°. Therefore:
m ∠ CDE + m ∠ EDF = 180°
(2 · x + 1) + (x - 7) = 180°
3 · x - 6 = 180°
3 · x = 186°
x = 62
m ∠ CDE = 2 · x + 1
m ∠ CDE = 2 · 62 + 1
m ∠ CDE = 125°
m ∠ ADC = 180° - 125°
m ∠ ADC = 55°
To learn more on supplementary angles: https://brainly.com/question/29117467
#SPJ1
Divide the following numbers. 4,084 / 1,016
Answers
The answer is 4 while rounding. If you need the exact answer, it is 4.019685039370
How many schools have fewer than 50 classrooms

Answers
Answer:
7 schools have fewer than 50 classrooms.
finding values of products and quotient functions
\(( \frac{r}{s} )(3) = \)
(3) = [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fo6qtw13QDITrL0XHWTkFEFXENPGcfQd.jpeg)
Answers
The product and the quotient of the functions are as follows:
(rs)(4) =8
(r / s)(3) = 2
How to solve function?A function relates input and output. It relates an independent variable with a dependent variable.
Therefore, let's solve the function as follows:
r(x) = 2√x
s(x) = √x
Therefore, let's find
(rs)(4) = r(4) × s(4) = 2√4 × √4 = 4 × 2 = 8
Let's find
(r / s)(3) = r(3) / s(3) = 2√3 / √3 = 2
Therefore,
(rs)(4) =8
(r / s)(3) = 2
learn more on function here: https://brainly.com/question/17430065
#SPJ1
There are six pizzas there are 36 players on the team. If each member has one slice and each pizza has eight slices how much pizza in fraction form will be left over.
Answers
There will be 12 slices of pizza left over, which can be expressed as 3/2 or 1 1/2 slices in fraction form.
To find out how much pizza will be left over, we need to calculate the total number of slices available and subtract the number of slices consumed by the players.
Given that there are six pizzas and each pizza has eight slices, the total number of slices available is 6 pizzas * 8 slices/pizza = 48 slices.
Since there are 36 players on the team, and each player has one slice, the total number of slices consumed is 36 slices.
To determine the remaining slices, we subtract the consumed slices from the total available slices: 48 slices - 36 slices = 12 slices.
Therefore, there will be 12 slices of pizza left over.
To express this as a fraction, we can write it as 12/1, which simplifies to 12. This means there will be 12 whole slices of pizza left over.
If you would like to express it as a fraction in its simplest form, you can write it as 12/8. By dividing both the numerator and denominator by their greatest common divisor, which is 4, we get 3/2. So, in fraction form, there will be 3/2 or 1 1/2 slices of pizza left over.
for more questions on fraction
https://brainly.com/question/78672
#SPJ8
Calc question — related rates

Answers
The rate at which the depth of the liquid is increasing when the depth of the liquid reaches one-third of the height of the bowl is 1.25 cm s⁻¹.
How to determine rate?The volume of the liquid in the bowl is given by the following integral:
\(V = \int\limitsx_{0}^{h} \, \pi r^{2}(y) dy\)
where r = radius of the bowl and y = height of the liquid.
The radius of the bowl is equal to the distance from the curve y = (4/(8-x)) - 1 to the y-axis. This can be found using the following equation:
r = √{(4/(8-x)) - 1}² + 1²
The height of the liquid is equal to the distance from the curve y = (4/(8-x)) - 1 to the x-axis. This can be found using the following equation:
h = (4/(8-x)) - 1
Substituting these equations into the volume integral:
\(V = \int\limitsx_{0}^{h } \, \pi {\sqrt{(4/(8-x)) - 1)^{2} + 1^{2} (4/(8-x))} - 1 dy\)
Evaluate this integral using the following steps:
Expand the parentheses in the integrand.
Separate the integral into two parts, one for the integral of the square root term and one for the integral of the linear term.
Integrate each part separately.
The integral of the square root term can be evaluated using the following formula:
\(\int\limits^{b} _{a} \, dx \sqrt{x} dx = 2/3 (x^{3/2}) |^{b}_{a}\)
The integral of the linear term can be evaluated using the following formula:
\(\int\limits^{b} _{a} \, {x} dx = (x^{2/2}) |^{b}_{a}\)
Substituting these formulas into the integral:
V = π { 2/3 (4/(8-x))³ - 1/2 (4/(8-x))² } |_0^h
Evaluating this integral:
V = π { 16/27 (8-h)³ - 16/18 (8-h)² }
The rate of change of the volume of the liquid is given by:
dV/dt = π { 48/27 (8-h)² - 32/9 (8-h) }
The rate of change of the volume of the liquid is 7π cm³ s⁻¹. Also the depth of the liquid is one-third of the height of the bowl. This means that h = 2/3.
Substituting these values into the equation for dV/dt:
dV/dt = π { 48/27 (8-2/3)² - 32/9 (8-2/3) } = 7π
Solving this equation for the rate of change of the depth of the liquid:
dh/dt = 7/(48/27 (8 - 2/3)² - 32/9 (8 - 2/3)) = 1.25 cm s⁻¹
Therefore, the rate at which the depth of the liquid is increasing when the depth of the liquid reaches one-third of the height of the bowl is 1.25 cm s⁻¹.
Find out more on linear equations here: https://brainly.com/question/14323743
#SPJ1
Select the correct answer.
What are the zeros of this quadratic function?
f(x) = (x − 7)(x + 8)
A.
x = 7 and x = -8
B.
x = -7 and x = 8
C.
x = 0 and x = -8
D.
x = 0 and x = 7
Answers
(x - 7) (x + 8)
Multiply the first x by both numbers in the second factor. Which means, you multiply x by x and 8, the two in (x + 8).
With this, you get -
x^2 + 8x
Then do the same thing with -7.
-7x - 56
Then combine the two.
x^2 + 8x - 7x - 56
Combine like terms.
x^2 + x - 56
So now, 7 x 8 is 56
And -7 + 8 would be 1. And that is the value of “x” which is b in the form a^2x + bx + c.
Now with this, you take those two numbers and make the factors =
(x + 8) (x - 7)
Then you set these equal to 0.
x + 8 = 0
Subtract the 8 from both sides.
x = -8
————
x - 7 = 0
Add the 7 on both sides.
x = 7
Answer: A
Answer:
The answer would be A
Step-by-step explanation:
You can find the answer by doing the FOIL method.
f(2) =
Evaluate functions from their graph

Answers
=====================================================
Explanation:
Check out the diagram below.
Draw a vertical line through 2 on the x axis.
This vertical line crosses the blue graph at some point, we'll call this point P.
Draw a horizontal line from point P to the y axis. You should arrive at y = -2
The input x = 2 leads to the output y = -2. The point (x,y) = (2,-2) is on the graph.
This means f(2) = -2.

Answer:
Evaluate functions from their graph f(2)= -5
Step-by-step explanation:
Randy has 386 hockey cards. he has 165 more baseball cards does he have in all
Answers
Answer:
just add 386+165 which equals 551
Step-by-step explanation: