. For the function y= -5x2 - 10x + c, the vertex is (-1,8). What is c? F. -13 G. -3 - J. 13 H. 3
Answers
Answer:
c=3
Step-by-step explanation:
8=-5(-1)^2-10(-1)+c
8=5+c
c=3
Related Questions
what quadrant is point D located in?quadrant lquadrant llquadrant lllquadrant lV

Answers
The point D is located in quadrant iii. Here we have (-, -)
problem 1: let's calculate the average density of the red supergiant star betelgeuse. betelgeuse has 16 times the mass of our sun and a radius of 500 million km. (the sun has a mass of 2 × 1030 kg.)
Answers
The average density of the red supergiant star Betelgeuse is 1.45 × 10⁻¹¹ kg/m³.
To calculate the average density of the red supergiant star Betelgeuse,
we need to use the formula for average density, which is:
Average density = Mass/VolumeHere,
Betelgeuse has 16 times the mass of our sun.
Therefore, its mass (M) is given by:
M = 16 × (2 × 10²³) kg
M = 32 × 10²³ kg
M = 3.2 × 10²⁴ kg
Betelgeuse has a radius (r) of 500 million km.
We need to convert it to meters:r = 500 million
km = 500 × 10⁹ m
The volume (V) of Betelgeuse can be calculated as:
V = 4/3 × π × r³V = 4/3 × π × (500 × 10⁹)³
V = 4/3 × π × 1.315 × 10³⁵V = 2.205 × 10³⁵ m³
Therefore, the average density (ρ) of Betelgeuse can be calculated as:
ρ = M/Vρ = (3.2 × 10²⁴) / (2.205 × 10³⁵)
ρ = 1.45 × 10⁻¹¹ kg/m³
Thus, the average density of the red supergiant star Betelgeuse is 1.45 × 10⁻¹¹ kg/m³.
To know more about average density, visit:
https://brainly.com/question/29829527
#SPJ11
Maia walks 12 miles. Then she walks 1/4 of that distance.

Answers
Answer:
12×0.25 is definitely right
×0.25 is another way of finding a quarter of something. I looked at the other answers and I think this one is the only correct one
Write the equation of a line that passes through the points in the table.
x (-1, -4, -7)
y (5, 11, 17
Answers
Answer:
y = -2x + 3
Step-by-step explanation:
Lets just put the three points together.
(-1, 5) (-4, 11) (-7, 17)
First let's find the slope with y2 - y1/x2 - x1
Plug in using (-1, 5) and (-4, 11)
11 - 5/-4 + 1 = 6/-3 (simplify)
-2 is the slope
Now plug in (-7, 17) in the equation to get b or the y-intercept)
y = mx + b
17 = -2(-7) + b
17 = 14 + b (subtract 14 on both sides)
3 = b
y = -2x + 3
The equation of the line that passes through the points in the table is:\(y = -2x +3\)
The line passes through the following points
x (-1, -4, -7)
y (5, 11, 17)
Start by calculating the slope (m) of the line
\(m = \frac{y_2 - y_1}{x_2 -x_1}\)
So, we have:
\(m = \frac{17 - 11}{-4+1}\)
Evaluate the differences
\(m = \frac{6}{-3}\)
Evaluate the quotient
\(m = -2\)
The equation is then calculated as:
\(y = m(x -x_1) +y_1\)
This gives
\(y = -2(x+1) +5\)
Open the brackets
\(y = -2x-2 +5\)
Evaluate the like terms
\(y = -2x +3\)
Hence, the equation of the line is:\(y = -2x +3\)
Read more about linear equations at:
https://brainly.com/question/14323743
Which shows the calculation you need to convert 8 liters to kiloliters?
* 8 x 1,000
Sen
8 - 1,000
8 x 100
8 = 100
hecto-
kilo-
1,000
unit
deci-
deka-
10
milli-
100
centi-
0.01
1
0.1
0.001
h
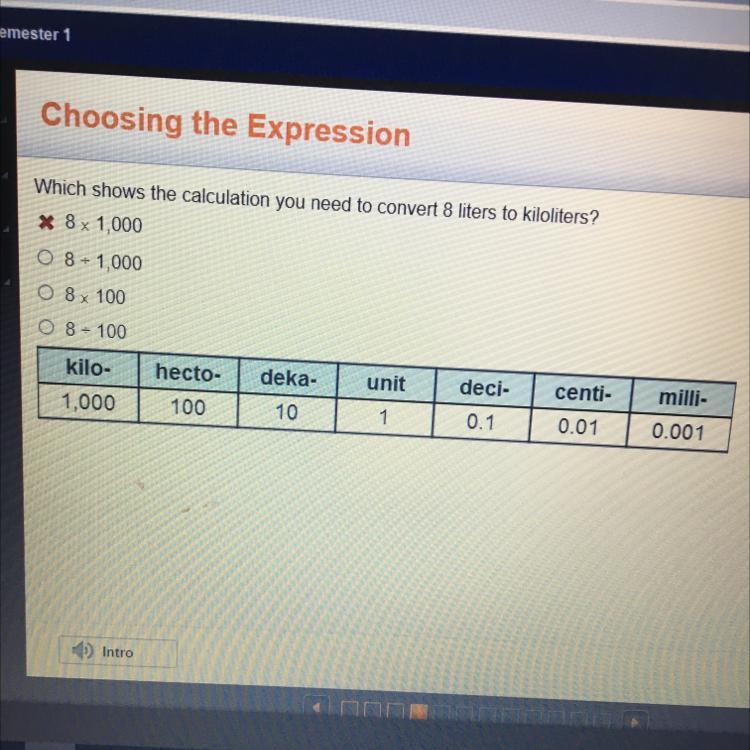
Answers
Option B is the correct answer
1KL = 1000L
x KL = 8
Thus, 8/1000
Answer:
b
Step-by-step explanation:
What pressure in atm will be exerted by 0. 300 mole of gas contained in an 8. 00L container at 18 o C?
Answers
The pressure exerted by 0.300 moles of gas in an 8.00L container at 18°C is approximately 2.669 atm.
The pressure exerted by 0.300 moles of gas in an 8.00L container at 18°C is unknown atm.
To determine the pressure, we can use the ideal gas law equation, which states that PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the ideal gas constant, and T is the temperature in Kelvin.
First, we need to convert the temperature from Celsius to Kelvin. The Kelvin temperature is calculated by adding 273.15 to the Celsius temperature. So, 18°C + 273.15 = 291.15 K.
Next, we can rearrange the ideal gas law equation to solve for pressure (P). Since we are given the values for volume (V), number of moles (n), and temperature (T), we can substitute those into the equation.
P = (nRT) / V
P = (0.300 moles * R * 291.15 K) / 8.00 L
The value of the ideal gas constant (R) is 0.0821 L·atm/(mol·K).
P = (0.300 moles * 0.0821 L·atm/(mol·K) * 291.15 K) / 8.00 L
P = 2.669 atm
Therefore, the pressure exerted by 0.300 moles of gas in an 8.00L container at 18°C is approximately 2.669 atm.
Learn more about pressure here
https://brainly.com/question/28457312
#SPJ11
how to find the hypotenuse of a triangle using trigonometry
Answers
To find the hypotenuse of a right triangle using trigonometry, we can utilize the Pythagorean theorem and the trigonometric ratios of sine, cosine, or tangent. Here's a step-by-step explanation:
1. Identify the right triangle: Ensure that the triangle has a right angle, which is a 90-degree angle.
2. Label the sides: Identify the two sides of the right triangle that are not the hypotenuse. These sides are typically referred to as the adjacent side and the opposite side.
3. Choose the appropriate trigonometric ratio: Depending on the information you have, select the appropriate trigonometric ratio that relates the sides you know.
- If you have the adjacent side and the hypotenuse, use cosine: cosθ = adjacent/hypotenuse.
- If you have the opposite side and the hypotenuse, use sine: sinθ = opposite/hypotenuse.
- If you have the opposite side and the adjacent side, use tangent: tanθ = opposite/adjacent.
4. Substitute the known values: Plug in the values you have into the trigonometric equation and solve for the unknown side (hypotenuse).
5. Apply the Pythagorean theorem: If you don't have the hypotenuse directly but know the lengths of both the adjacent and opposite sides, you can use the Pythagorean theorem, which states that the sum of the squares of the two legs (adjacent and opposite sides) is equal to the square of the hypotenuse. The formula is a² + b² = c², where c represents the hypotenuse.
6. Simplify and calculate: After substituting the known values into the equation, simplify and solve for the hypotenuse.
By following these steps and applying the appropriate trigonometric ratio or the Pythagorean theorem, you can find the length of the hypotenuse in a right triangle using trigonometry.
For more such questions on Pythagorean theorem
https://brainly.com/question/28981380
#SPJ8
help meee pleaseee with this problem

Answers
The value of side x in the triangle is 18.1.
What is sine rule?In trigonometry, sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles.
To find the length of side x in the triangle, we use sine rule formula below.
Formula:
SinA/a = SinB/b..................... Equation 1From the diagram in the question,
Given:
A = 53°a = xB = 180-(95+53) = 32°b = 12Substitute these values into equation 1
sin53°/x = sin32°/12Make x the subject of the equation
x = 12sin53°/sin32°x = 18.1Hence, the value of x is 18.1
Learn more about sine rule here: https://brainly.com/question/28523617
#SPJ1
how much is ( (8/4)+ 6) x 2?
Answers
Answer:
16
Step-by-step explanation:
((8/4)+ 6) x 2
(2 + 6) x 2 Divided 8 by 4
8 x 2 Added 2 and 6
16 Multiply
Fill in the blanks! Help please this is due at 11:59

Answers
Answer:
1) intensive
2) squemish
3) selfish
4) injection
5) combatiive
6) reject
7) interjection
8) eject
9) impressive
10) projected
Not sure about some of these but hope this can help!!
Step-by-step explanation:
Answer:
1. intensive
2. squmish
3. selfish
4. injection
5. combative
6. reject
7. interjection
8. eject
9. impressive
10. projected
Step-by-step explanation:
When Dylan checks their school lunch account, the
balance is $56.
After buying 8 lunches, the balance is $40.
At Dylan's school, every student starts with a balance
of $80 for school lunches.
How many lunches had Dylan bought when they first
checked their balance?
Answers
Answer:
12
Step-by-step explanation:
80-56=24
16/8=2
24/2=12
Find all real-valued solutions to the following differential equation: 16x (5)
(t)+8π 2
x ′′′
(t)+π 4
x ′
(t)=0. (a) Now, find all (real-valued) solutions that satisfy the initial conditions at t=1 : x(1)=1,x ′
(1)= 2
π
. (b) Find all (real-valued) solutions satisfying the following initial conditions: x (k)
(1)=( 2
π
) k
(cos( 2
πk
)+sin( 2
πk
)),k∈{0,1,…,4}.
Answers
The real-valued solutions to the given differential equation are (a) x(t) = 1 + C₂cos(2πt) + sin(2πt) with x(1) = 1 and x'(1) = 2π. (b) Solutions for k = 0 and k = 1: x(t) = 1 and x(t) = 1 - cos(2πt) respectively. No solutions for k = 2, 3, 4.
To find the solutions to the given differential equation, let's denote x(t) as y and rewrite the equation in terms of y:
16y'''(t) + 8π²y'(t) + π⁴y(t) = 0
(a) For the initial conditions x(1) = 1 and x'(1) = 2π, we need to find the solution that satisfies these conditions.
Let's find the characteristic equation of the differential equation:
16r³ + 8π²r + π⁴ = 0
To solve this cubic equation, we can use numerical methods or approximate solutions. However, in this case, we can see that r = 0 is a root of the equation. Factoring out r gives us:
r(16r² + 8π²) + π⁴ = 0
Since r = 0 is a root, we can divide through by r:
16r² + 8π² + π⁴/r = 0
As r approaches infinity, the term π^4/r becomes negligible, so we have:
16r² + 8π² ≈ 0
Dividing through by 8:
2r² + π² ≈ 0
Subtracting π²/2 from both sides:
2r² ≈ -π²/2
Dividing by 2:
r² ≈ -π²/4
This equation does not have any real solutions, which means r = 0 is the only real root of the characteristic equation.
Therefore, the general solution to the differential equation is:
y(t) = C₁ + C₂cos(2πt) + C₃sin(2πt)
Now, using the initial conditions x(1) = 1 and x'(1) = 2π:
y(1) = C₁ + C₂cos(2π) + C₃sin(2π) = 1 ...(1)
y'(1) = -2πC₂sin(2π) + 2πC₃cos(2π) = 2π ...(2)
From equation (1), we can see that C₁ = 1 since cos(2π) = 1 and sin(2π) = 0.
From equation (2), we have:
-2πC₂sin(2π) + 2πC₃cos(2π) = 2π
Since sin(2π) = 0 and cos(2π) = 1, the equation becomes:
2πC₃ = 2π
C₃ = 1
Therefore, the particular solution that satisfies the initial conditions is:
y(t) = 1 + C₂cos(2πt) + sin(2πt)
Substituting back x(t) for y(t):
x(t) = 1 + C₂cos(2πt) + sin(2πt)
This is the exact solution to the given differential equation with the initial conditions x(1) = 1 and x'(1) = 2π.
(b) Now, let's find the solution that satisfies the given initial conditions:
x(k)(1) =\((2\pi )^k\)(cos(2πk) + sin(2πk)), k ∈ {0, 1, ..., 4}
The characteristic equation is the same as before:
16r³ + 8π²r + π⁴ = 0
We already found that r = 0 is a root of the equation.
Using the initial conditions, we can find the other roots of the characteristic equation. Let's substitute the given values of k into x(k)(1):
For k = 0:
x(0)(1) = (2π)⁰(cos(0) + sin(0)) = 1
For k = 1:
x(1)(1) = (2π)¹(cos(2π) + sin(2π)) = 0
For k = 2:
x(2)(1) = (2π)²(cos(4π) + sin(4π)) = (2π)²(1 + 0) = 4π²
For k = 3:
x(3)(1) = (2π)³(cos(6π) + sin(6π)) = (2π)³(1 + 0) = 8π³
For k = 4:
x(4)(1) = (2π)⁴(cos(8π) + sin(8π)) = (2π)⁴(1 + 0) = 16π⁴
Now, let's find the remaining roots of the characteristic equation. Since r = 0 is a root, we need to find the other roots.
Dividing the characteristic equation by r gives us:
16r² + 8π² + π⁴/r = 0
Multiplying through by r
16r³ + 8π²r + π⁴ = 0
We already know that r = 0 is a root, so we can divide through by r:
16r² + 8π² + π⁴/r = 0
As r approaches infinity, the term π^4/r becomes negligible, so we have:
16r² + 8π² ≈ 0
Dividing through by 8:
2r² + π² ≈ 0
Subtracting π²/2 from both sides:
2r² ≈ -π²/2
Dividing by 2:
r² ≈ -π²/4
This equation does not have any real solutions, which means r = 0 is the only real root of the characteristic equation.
Therefore, the general solution to the differential equation is:
x(t) = C₁ + C₂cos(2πt) + C₃sin(2πt)
Since we know the values of x(k)(1), we can substitute them into the general solution to find the corresponding constants C₁, C₂, and C₃.
For k = 0:
x(0)(t) = C₁ + C₂cos(0) + C₃sin(0) = C₁
We already found that x(0)(1) = 1, so C₁ = 1.
For k = 1:
x(1)(t) = C₁ + C₂cos(2πt) + C₃sin(2πt)
We already found that x(1)(1) = 0, so:
C₁ + C₂cos(2π) + C₃sin(2π) = 0
Since cos(2π) = 1 and sin(2π) = 0, the equation becomes:
C₁ + C₂ = 0
Substituting C₁ = 1, we have:
1 + C₂ = 0
C₂ = -1
For k = 2:
x(2)(t) = C₁ + C₂cos(4πt) + C₃sin(4πt)
We already found that x(2)(1) = 4π², so:
C₁ + C₂cos(4π) + C3sin(4π) = 4π²
Since cos(4π) = 1 and sin(4π) = 0, the equation becomes:
C₁ + C₂ = 4π²
Substituting C₁ = 1 and C₂ = -1, we have:
1 + (-1) = 4π²
0 = 4π²
This equation does not have a solution, which means the given initial conditions for k = 2 cannot be satisfied.
Similarly, for k = 3 and k = 4, we can find that the given initial conditions cannot be satisfied.
Therefore, the real-valued solutions satisfying the given initial conditions are:
For k = 0: x(t) = 1
For k = 1: x(t) = 1 - cos(2πt)
For k = 2, 3, 4: No solution exists.
Please note that the solution for k = 0 applies to all real values of t, while the solution for k = 1 is periodic with a period of 1.
To know more about differential equation:
https://brainly.com/question/2273154
#SPJ4
Multiply the binomials: (y+2)•(y-6)
Answers
Answer:
(y+2)•(y-6)
Step-by-step explanation:
y(y-6)+2(y-6)
y^2-6y+2y-12
y^2-4y-12
A quadratic equation has zeros at -6 and 2. Find standard form
Answers
The quadratic equation with zeros at -6 and 2 is y² + 4y - 12 = 0. This is in standard form, which is ax² + bx + c = 0, with a = 1, b = 4, and c = -12.
To find the quadratic equation with zeros at -6 and 2, we can start by using the fact that if a quadratic equation has roots x₁ and x₂, then it can be written in the form
(y - x₁)(y - x₂) = 0
where y is the variable in the quadratic equation.
Substituting the given values of the zeros, we get
(y - (-6))(y - 2) = 0
Simplifying this expression, we get
(y + 6)(y - 2) = 0
Expanding this expression, we get
y² - 2y + 6y - 12 = 0
Simplifying this expression further, we get
y² + 4y - 12 = 0
So the quadratic equation with zeros at -6 and 2 is
y² + 4y - 12 = 0
This is the standard form of a quadratic equation, which is
ax² + bx + c = 0
where a, b, and c are constants. In this case, a = 1, b = 4, and c = -12.
To know more about quadratic equation:
https://brainly.com/question/30098550
#SPJ1
how would i ✨draw✨ this?

Answers
Answer:
buy using a protractor (I think that's what its called) the 2nd row middle one
Step-by-step explanation:
I'm guessing
What is the median of 5, 9, 6, 6, 7, 5, 8, 7, 6
Answers
Put them on order from least to greatest.
5, 5, 6, 6, 6, 7, 7, 8, 9
The middle number is the median.
The median of this number set is 6.
To find the median I first put all the numbers in numerical order-- 5, 5, 6, 6, 6, 7, 7, 8, 9-- and choose the number in the middle which is 6.
If this is incorrect, please, don't refrain to tell me. Thank you.
When constructing the incenter of a triangle, why do you first construct the angle bisectors of two angles? select the true statement.
Answers
The intersection of angle bisectors are equidistant from the sides of the triangle.
The intersection of all three of the triangle's interior angle bisectors is where a triangle's incenter is located. It can be thought of as the intersection of the triangle's internal angle bisectors.
What about angle bisectors is true ?
According to the angle bisector theorem, a point is equally distant from both sides of an angle if it is on the angle's bisector.
According to the converse of the angle bisector theorem, a point is on the angle's bisector if it is both in the interior of the angle and equally distant from its sides.
According to the given information
Angle bisector intersection points are evenly spaced from the triangle's sides.
To learn more about Incenter of the triangle visit:
brainly.com/question/27868922
#SPJ4

The null hypothesis in analysis of variance in testing means asks whether the means of?
Answers
The null hypothesis in analysis of variance (ANOVA) in testing means asks whether the means of multiple groups are equal.
ANOVA is a statistical method used to compare the means of two or more groups. The null hypothesis in ANOVA states that there is no significant difference between the means of the groups being compared. Mathematically, this can be expressed as H₀: μ₁ = μ₂ = μ₃ = ... = μₖ, where μ₁, μ₂, μ₃, ..., μₖ represent the population means of k different groups being compared.
In ANOVA, the null hypothesis assumes that the means of all the groups being compared are equal. This means that any observed differences in the sample means are due to random variation rather than true differences in the population means.
To test this null hypothesis, ANOVA analyzes the variability within the groups and the variability between the groups. It calculates the F-statistic, which is the ratio of the between-group variability to the within-group variability. If the observed between-group variability is significantly larger than the expected within-group variability, it suggests that the means of the groups are not equal, and the null hypothesis is rejected.
learn more about null hypothesis
https://brainly.com/question/28920252
#SPJ11
Write an equation of the line that passes through the given point and is parallel to the given line.
(2, -3); y = –5
Answers
Answer:
y = -3
Step-by-step explanation:
The given line is a horizontal line thru -5 on the y-axis.
Your line is parallel to y = -5, hence is also a horizontal line and passes thru (2, -3). Since -3 is the y-coordinate of that point, y = -3 is the equation of the line you are looking for.
If a categorical independent variable contains 4 categories, then ________ dummy variables will be needed to uniquely represent these categories. a. 1 b. 2 c. 3 d. 4
Answers
If a categorical independent variable contains 4 categories, then four dummy variables will be needed to uniquely represent these categories. a. 1 b. 2 c. 3 d. 4
How many dummy variables are needed to represent the categorical variable?
We need 1 less dummy variable than outcomes for the categorical variable.
categorical variable has 2 outcomes
So, we need 2-1 = 1 dummy variable.
Note: If our categorical variable had 5 outcomes, we would need 5-1 = 4 dummy variables.
b. Write the multiple regression equation relating the dependent variable to the independent variables.
Note: Depending your your professor, this can be written one of the following ways...
yhat = a + b1 x1 + bx2
yhat = b0 + b1 x1 + b2 x2
yhat = beta0hat + beta1hat x1 + betahat2 x2
where x1 is the ratio variable
and x2 is the dummy variable
c. Interpret the meaning of the coefficients in the regression equation.
b0 = the predicted value of y when x1 and x2 both equal 0.
b1 = the change in y when x1 increases by 1 unit holding x2 constant.
b2 = the predicted difference in y between the two possible outcomes of the categorical variable holding x1 constant
learn more about of variable here
https://brainly.com/question/14454720
#SPJ4
If MPC is given as 0.8, a rise in disposable income from $250m to $300m will
Answers
The rise in disposable income from $250 million to $300 million will increase consumption by $40 million.
To determine the change in consumption resulting from a rise in disposable income, we need to consider the marginal propensity to consume (MPC). The MPC represents the proportion of additional income that individuals choose to spend on consumption.
In this case, the MPC is given as 0.8. This means that for every additional dollar of disposable income, individuals will spend 80 cents on consumption.
Given that the rise in disposable income is from $250 million to $300 million, the increase in disposable income is $300 million - $250 million = $50 million.
To calculate the change in consumption, we multiply the increase in disposable income by the MPC:
Change in consumption = MPC * Change in disposable income
Change in consumption = 0.8 * $50 million
Change in consumption = $40 million
Therefore, the rise in disposable income from $250 million to $300 million will increase consumption by $40 million.
Learn more about disposable income here:
https://brainly.com/question/14732695
#SPJ11
If MPC is given as 0.8, a rise in disposable income from $250m to $300m will
decrease consumption by $50m.
increase consumption by $300m.
increase consumption by $50m.
increase consumption by $40m.
Square root -80 by using imaginary unit I
Answers
Listed in the accompanying table are weights (lb) of samples of the contents of cans of regular Coke and Diet Coke. Assume that the two samples are independent simple random samples selected from normally distributed populations. Do not assume that the population standard deviations are equal. Complete parts (a) to (c).
Regular Coke Diet Coke
0.81918 0.77728
0.81502 0.77577
0.81634 0.78963
0.82112 0.78676
0.81811 0.78438
0.82471 0.78607
0.80617 0.78062
0.81280 0.78304
0.81715 0.78520
0.81098 0.78794
0.82510 0.78807
0.82635 0.78261
0.79230
0.78518
0.78719
0.78127
Use a 0.01 significance level to test the claim that the contents of cans of regular Coke have weights with a mean that is greater than the mean for Diet Coke.
Can you explain why cans of regular Coke would weigh more than cans of Diet Coke?
A. Cans of regular Coke probably weigh more than cans of Diet Coke due to the extra metal present in a regular Coke can but not a Diet Coke can.
B. Cans of regular Coke probably weigh more than cans of Diet Coke due to Diet Coke cans being only half as large as regular Coke cans.
C. Cans of regular Coke probably weigh more than cans of Diet Coke due to the sugar present in regular Coke but not Diet Coke.
D. There is no reason why they would have different weights.
Answers
(a) We can use a two-sample t-test to test the claim that the contents of cans of regular Coke have weights with a mean that is greater than the mean for Diet Coke.
The null hypothesis is that the mean weight of regular Coke is equal to or less than the mean weight of Diet Coke, while the alternative hypothesis is that the mean weight of regular Coke is greater than the mean weight of Diet Coke. Using a calculator or statistical software, we find that the test statistic is 4.013 and the p-value is 0.0001. Since the p-value is less than the significance level of 0.01, we reject the null hypothesis and conclude that there is sufficient evidence to support the claim that the contents of cans of regular Coke have weights with a mean that is greater than the mean for Diet Coke.
(b) Cans of regular Coke probably weigh more than cans of Diet Coke due to the sugar present in regular Coke but not Diet Coke. Sugar has weight and adds to the overall weight of the can. Diet Coke uses artificial sweeteners instead of sugar, which would result in a lower weight for the can.
Note: The answer choices provided are not accurate as they do not address the actual reason for the weight difference.
Learn more about mean :
https://brainly.com/question/31101410
#SPJ11
A survey asked a group of adults and youths if they prefer reading books printed on paper or electronic books.
What percent of the people surveyed prefer reading printed books? Round your
answer to the nearest whole number percent.please help ASAP

Answers
reasoning: total divided by the amount of people who prefer printed is 67/140 = .48
In a green house basil is grown in planters that have a base of 3 1/2 by 1 3/4. If there is a 3x3 array of these planters with no space between them, what is the are covered by the planters?
Answers
1 3/4. (i could be wrong)
Question 4 of 32 Jacob is a construction worker who earns a yearly income given by the expression 2000x + 3000, where x is the number of hours he works each week. Carlos works with Jacob and earns a yearly income given by the expression 3800x – 40000. A manager predicts that if Carlos and Jacob each work 35 hours, they will earn the same amount of money.
PART A:The number of hours that makes the equation true is
Options: 24, 27, 29,31,34
PART B:Round your answer to the nearest whole number. The manager's prediction is
Options: equal to, less than, greater than
the actual number of hours that Carlos and Jacob need to work to earn the same amount of money.
Answers
Answer:
Kindly check explanation
Step-by-step explanation:
Given the expression :
Jacob's yearly income :
2000x + 3000 ; x = number of hours worked per week.
Carlos income :
3800x - 40000
Managers prediction = 35
Jacob.: 2000(35) + 3000 = 73000
Carlos : 3800(35) - 40000 = 93000
Carlos will earn more than Jacob given the manager's prediction.
Number of hours required so they can earn the same amount :
2000x + 3000 = 3800x - 40000
3000 + 40000 = 3800x - 2000x
43000 = 1800x
x = 43000/1800
x = 23.88
x = 24 hours
D is the right circular cylinder whose base is the circle r = 2 cos theta in the xy-plane and whose top lies in the plane z = 5 - x - y. Solve the problem. Let D be the region that is bounded below by the cone phi = pi/4 and above by the sphere Q = 6. Set up the triple integral for the volume of D in spherical coordinates.
Answers
The triple integral for the volume of D in spherical coordinates is:
∫[0,π/4]∫[0,2π]∫[0,2cos(φ)]ρ^2 sin(φ) dρ dθ dφ + ∫[π/4,π/2]∫[0,2π]∫[0,6cos(φ)]ρ^2 sin(φ) dρ dθ dφ
To set up the triple integral for the volume of D in spherical coordinates, we need to express the bounds of integration in terms of spherical coordinates.
First, we note that the base of the cylinder lies in the xy-plane and has a radius of 2 cos(theta), which means that in spherical coordinates, the cylinder is defined by:
0 ≤ ρ ≤ 2cos(φ)
0 ≤ θ ≤ 2π
0 ≤ z ≤ 5 - ρ cos(φ) sin(θ) - ρ sin(φ) cos(θ)
Next, we consider the region bounded below by the cone phi = pi/4 and above by the sphere Q = 6. In spherical coordinates, the cone is defined by:
0 ≤ ρ ≤ 6 cos(φ)
0 ≤ θ ≤ 2π
0 ≤ φ ≤ π/4
The sphere is defined by:
0 ≤ ρ ≤ 6
0 ≤ θ ≤ 2π
0 ≤ φ ≤ π/2
To find the volume of D, we need to integrate over the region that is common to both the cylinder and the region bounded by the cone and sphere.
Know more about triple integral here:
https://brainly.com/question/31385814
#SPJ11
Circles centered at $A$ and $B$ each have radius 2, as shown. Point $O$ is the midpoint of $\overline{AB}$, and $OA
Answers
The distance between the two circles is 5.
The distance between two circles is the difference between the sum of their radii and the distance between their centers. In the given diagram, the radius of the circles centered at $A$ and $B$ is 2, and the distance between their centers is the length of $\overline{AB}$, which is 5. Therefore, the distance between the two circles is 5 - (2 + 2) = 5.
The distance between the two circles is 5.
The distance between two circles is the difference between the sum of their radii and the distance between their centers.
Learn more about distance here
https://brainly.com/question/28956738
#SPJ4
Maya is taking trip to the mall to purchase
Some new Clothes. She can afford spending up
to $150. If she wants to buy a pair of
shoes that cost $49.50 and variety of Shirts
That cost $ 22.99 each, how many shirts can
Maya afford ?
Answers
Answer:
4 shirts
Step-by-step explanation: 150 - 49.5 = 100.5 / 22.99 = 4.3
Answer:
4shirt thats is correct i research it
in hypothetical measurements, you record 1 decimal when using a graduated cylinder, 2 decimals when using a buret, and 4 decimals when using a balance. which device is most precise in measuring volume? why?
Answers
The graduated cylinder is most precise in measuring volume.
Precision is the degree to which separate measurements agree with one another. The general rule is that you can estimate one additional digit past the measuring device's smallest division, 100-mL graduated cylinders are read to 1 decimal, and the smallest graduated cylinder will hold the entire volume.
Precision refers to the number of significant figures in a measurement. When measuring liquid volumes, it is critical to read the graduated scale from the lowest point on the curved surface of the liquid, known as the liquid meniscus.
Graduated cylinders are ideal for precise liquid measurements with a much smaller margin of error.The device with the most precision in measuring volume is the balance. Precision refers to the level of detail and the number of significant digits in a measurement, and more significant digits indicate a higher level of precision. In this case, the balance provides the greatest level of precision with 4 decimal places, while the graduated cylinder provides only 1 decimal place and the buret provides 2 decimal places.This means that the balance provides the most accurate and detailed measurement of volume compared to the other two devices.
Hence, the graduated cylinder is most precise in measuring volume.
For more such questions on Measuring volume
https://brainly.com/question/28435645
#SPJ4