For some painkillers, the size of the dose, D, given depends on the weight of the patient, W. Thus, D = f(W), where D is in milligrams and W is in pounds. (a) Interpret the statements f(130) = 123 and f'(130) = 3 in terms of this painkiller. f(130) = 123 means f'(130) = 3 means (b) Use the information in the statements in part (a) to estimate f(136). f(136) = i mg
Answers
(a) The statement f(130) = 123 means that for a patient weighing 130 pounds, the prescribed dose of the painkiller is 123 milligrams.
This indicates that the function f(W) provides the dosage recommendation based on the weight of the patient.
The statement f'(130) = 3 means that the derivative of the function f(W) with respect to weight, evaluated at 130 pounds, is 3.
This indicates that for every additional pound in weight, the recommended dosage increases by 3 milligrams.
(b) To estimate f(136), we can use the information given in part (a). Since f'(130) = 3, we can approximate the change in dosage per pound as a constant rate of 3 milligrams.
From 130 to 136 pounds, there is an increase of 6 pounds.
Therefore, we can estimate f(136) by adding 6 times the rate of change to the initial dosage of f(130). Thus, f(136) ≈ 123 + (6 × 3) = 141 mg.
Based on this estimation, the recommended dose for a patient weighing 136 pounds would be approximately 141 milligrams.
Learn more about prescribed dose here: brainly.com/question/14710829
#SPJ11
(a) The statement f(130) = 123 means that for a patient weighing 130 pounds, the prescribed dose of the painkiller is 123 milligrams.
(b) The recommended dose for a patient weighing 136 pounds would be approximately 141 milligrams.
(a) This indicates that the function f(W) provides the dosage recommendation based on the weight of the patient.
The statement f'(130) = 3 means that the derivative of the function f(W) with respect to weight, evaluated at 130 pounds, is 3.
This indicates that for every additional pound in weight, the recommended dosage increases by 3 milligrams.
The statement f(130) = 123 means that for a patient weighing 130 pounds, the prescribed dose of the painkiller is 123 milligrams.
(b) To estimate f(136), we can use the information given in part (a). Since f'(130) = 3, we can approximate the change in dosage per pound as a constant rate of 3 milligrams.
From 130 to 136 pounds, there is an increase of 6 pounds.
Therefore, we can estimate f(136) by adding 6 times the rate of change to the initial dosage of f(130). Thus, f(136) ≈ 123 + (6 × 3) = 141 mg.
Based on this estimation, the recommended dose for a patient weighing 136 pounds would be approximately 141 milligrams.
Learn more about prescribed dose here: brainly.com/question/14710829
#SPJ11
Related Questions
the polynomial (x-2) is a factor of the polynomial 3x^2-8x 2
Answers
The polynomial (x-2) is not a factor of the polynomial \(3x^2\) - 8x + 2. Therefore, the given statement is false.
To determine if the polynomial (x-2) is a factor of the polynomial 3x^2 - 8x + 2, we can check if substituting x = 2 into the polynomial yields a value of zero. If the result is zero, then (x-2) is a factor.
Substituting x = 2 into \(3x^2\) - 8x + 2, we get:
3(2)^2 - 8(2) + 2 = 12 - 16 + 2 = -2
Since the result is not zero, we can conclude that (x-2) is not a factor of the polynomial \(3x^2\) - 8x + 2.
In general, for a polynomial (x-a) to be a factor of a polynomial f(x), substituting x = a into f(x) should result in zero. If the result is not zero, then (x-a) is not a factor of f(x).
Learn more about factor here:
https://brainly.com/question/14549998
#SPJ11
b) Here are the first four terms of another sequence.
6 11 16 21
Write an expression for the nth term of this sequence.
Answers
Answer:
aₙ = 5n + 1Step-by-step explanation:
11 - 6 = 5 , 16 - 11 = 5 , 21 - 16 = 5
So, it's atithmetic formula with common difference os 5
\(a_n = a_1+d(n-1)\\\\a_1=6\\d=5\\\\a_n=6+5(n-1)\\\\a_n=6 +5n-5\\\\a_n = 5n+1\)
how would I go about Simplify 2⁵ ÷ 2³
Answers
Answer:
2^8
Step-by-step explanation:
what is the solid of revolution obtained when you revolve the region bounded by the curves y equals x minus 1, y equals 0, and x equals 3 about the x-axis?
Answers
The height of the cylinder is 3 and its base is a circular disk with radius 1.
The solid of revolution obtained by revolving the region bounded by the curves y = x - 1, y = 0, and x = 3 about the x-axis is a cylinder.
The curves y = x - 1 and y = 0 bound a triangular region in the xy-plane with vertices (0, -1), (3, 0), and (1, 0). When this region is revolved about the x-axis, it generates a cylinder with height 3 and base a circular disk with radius 1.
A cylinder has traditionally been a three-dimensional solid, one of the most normal of curvilinear geometric shapes.
To know more about Cylinder:
https://brainly.com/question/16134180
#SPJ4
Select the number in which the digit 4 is ten times the value of the digit 4 in 6.141. Select all that apply.
A 8.436 B 6.34
C 41.8 D 4.13
E 0.864 F 83.41
Answers
Answer:
The answer would be A & F
Step-by-step explanation:
Aprobability experiment is conducted in which the sample space of the experiment is S-(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12), event F-(2, 3, 4, 5, 6), and event G(6, 7, 8, 9) Assume that each outcome
Answers
The probability of the P(F or G) is 0.667.
A probability experiment is conducted in which the sample space of the experiment is S={ 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}, event F={5, 6, 7, 8, 9}, and event G={9, 10, 11, 12}. Assume that each outcome is equally likely.
To list the outcomes in F or G, we need to combine both events F and G and eliminate any duplicates.
So, the outcomes in F or G are:
F or G = {5, 6, 7, 8, 9, 10, 11, 12}
Hence, A. F or G = { 5, 6, 7, 8, 9, 10, 11, 12}
Next, to find P(F or G) by counting the number of outcomes in F or G, we can use the formula:
P(F or G) = n(F or G) / n(S)
where, n(F or G) is the number of outcomes in F or G and n(S) is the number of outcomes in the sample space.
So, n(F or G) = 8 and n(S) = 12
Hence, P(F or G) = n(F or G) / n(S) = 8/12 = 0.667 (rounded to three decimal places)
Therefore, B. P(F or G) = 0.667
Finally, to determine P(F or G) using the general addition rule, we can use the formula:
P(F or G) = P(F) + P(G) - P(F and G)
where, P(F) and P(G) are the probabilities of events F and G, and P(F and G) is the probability of the intersection of events F and G.
To find P(F and G), we can use the formula:
P(F and G) = n(F and G) / n(S)
where, n(F and G) is the number of outcomes in both F and G.
So, n(F and G) = 1
Hence, P(F and G) = n(F and G) / n(S) = 1/12
Therefore, A. P(F or G) = (5/12) + (4/12) - (1/12) = 8/12 = 0.667 (rounded to three decimal places)
To learn more about probability refer here
https://brainly.com/question/32004014#
#SPJ11
Consider the equation f (x) = (x + 1): – 3.
Which point does NOT lie on the graph of y=f-? (x)?
Answers
Answer:
-3
Step-by-step explanation:
x+1=3
Compare the investment below to an investment of the same principal at the same rate compounded annually (look at picture below for details)
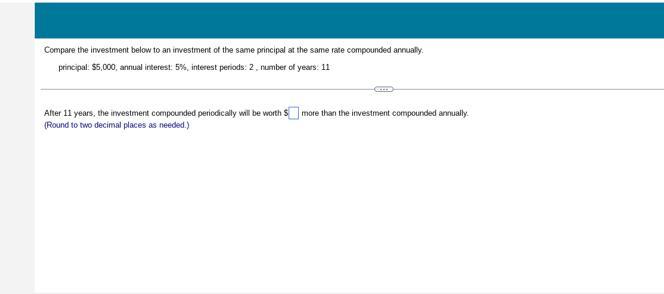
Answers
so we have two investments, one compounding annually and another compounding semi-annually, let's check both
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$5000\\ r=rate\to 5\%\to \frac{5}{100}\dotfill &0.05\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{semi-annually, thus twice} \end{array}\dotfill &2\\ t=years\dotfill &11 \end{cases} \\\\\\ A = 5000\left(1+\frac{0.05}{2}\right)^{2\cdot 11} \implies \boxed{A \approx 8607.86} \\\\[-0.35em] ~\dotfill\)
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$5000\\ r=rate\to 5\%\to \frac{5}{100}\dotfill &0.05\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{annually, thus once} \end{array}\dotfill &1\\ t=years\dotfill &11 \end{cases}\)\(A = 5000\left(1+\frac{0.05}{1}\right)^{1\cdot 11} \implies \boxed{A \approx 8551.70} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ semi-annually }{8607.86}~~ - ~~\stackrel{ annually }{8551.70} ~~ \approx ~~ \text{\LARGE 56.16}\)
Find X and Y such that X + Y = 500 and the difference between X and Y is 100.
Answers
Answer:
X=300, Y=200
Step-by-step explanation:
If: X+Y=500,
Then Y = 500-X
IF X-Y=100,
Then:
X-(500-X)=100,
X-500+X=100,
2X-500=100,
2X=100+500
2X=600
X=300.
So,
X+Y=500,
300+Y=500
Y=500-300
Y=200
So:
X=300, Y=200
Answer: X and Y = 300 + 200
Step-by-step explanation: Find two numbers that add up to 500 and make sure that you can subtract them and get 100.
Helpppp
Sharon made a list of attributes
4 sides
4 angles
2 pairs of parallel sides
2 pairs of congruent sides
Which shapes have ALL attributes?
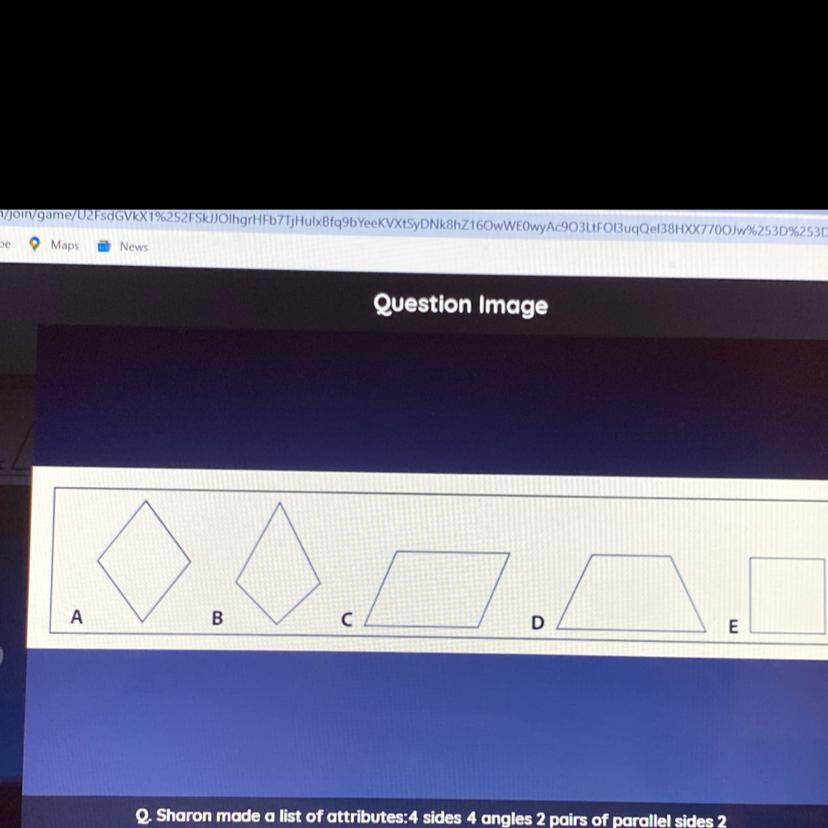
Answers
Find the Error A student states that the exterior angle of a triangle can never be a right angle. Choose the response that identifies the mistake
and corrects it.
O A) There is no mistake. The statement is correct.
OB) An exterior angle of a triangle can be supplementary to the right angle of a right triangle, so an exterior angle can be a right angle.
OC) An exterior angle of a triangle can be complimentary to an acute angle of a right triangle, so an exterior angle can be a right angle.
OD) An exterior angle of a triangle can be adjacent to the right angle of a right triangle, so an exterior angle can be a right angle.
Answers
Student is wrong An exterior angle of a triangle can be adjacent to the right angle of a right triangle, so an exterior angle can be a right angle.
What is exterior angle?The Exterior Angle is the angle between any side of a shape, and a line extended from the next side.
The student make an error he states that the exterior angle of a triangle can never be a right angle.
The correct answer will be option D that is An exterior angle of a triangle can be adjacent to the right angle of a right triangle, so an exterior angle can be a right angle.I have also attached the diagram of the triangle for better understanding.
To know more about exterior angle follow
https://brainly.com/question/2546141
#SPJ1

What best describes the value of (x - 5)(x - 10) when x = 10?
O Positive
O Negative
O Zero
Answers
A 16 ft ladder leans against a wall so that the base of the ladder is 5 ft away from the base of the wall. How far up the wall does the ladder reach.
Answers
Answer:
The ladder would reach 15.2 feet up
Distribute to write an equivalent expression. 2n * (n ^ 2 + 3n + 4)

Answers
Answer:
C. 2n^3 + 6n^2 + 8n
Explanation:
Tan θ is sometimes referred to as the slope of a decline or rise. What would be the angle of the rise of a bridge that rose 500 feet per one-half mile?
Answers
To find the angle of the rise of a bridge, given that it rises 500 feet per one-half mile, we can use the trigonometric function tangent (tan).
The tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle in a right triangle.
In this case, we can consider the height of the bridge (500 feet) as the side opposite the angle and the horizontal distance (one-half mile or 2640 feet) as the side adjacent to the angle.
Using the formula:
tan(θ) = opposite/adjacent
tan(θ) = 500/2640
To find the angle (θ), we can take the inverse tangent (arctan) of both sides:
θ = arctan(500/2640)
Using a calculator, we find that:
θ ≈ 11.22 degrees
Therefore, the angle of the rise of the bridge would be approximately 11.22 degrees.
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
Conider the following function. (If an anwer doe not exit, enter DNE. ) f(x) = e^−x2
Answers
The function has no vertical asymptotes and the horizontal asymptotes of the function is y=0.
In the given question,
Consider the following function.
f(x) = e^{−x^2}
We have to find the vertical asymptote(s), x = Find the horizontal asymptote(s) or y = .
As we know that, a vertical asymptote is a line that runs vertically and guides the graph of the function but does not actually exist on it. Due to its position at an x-value that is outside of function's domain, it is difficult for the curve to ever pass it.
The function f(x) = e^{−x^2} has no undefined points. So the function has no vertical asymptotes.
The limit of the function at x→±∞ is calculated as follows:
\(\lim_{x\rightarrow \pm\infty }\)f(x) = \(\lim_{x\rightarrow \pm\infty }\)e^{−x^2}
\(\lim_{x\rightarrow \pm\infty }\)f(x) = 0
So the horizontal asymptotes of the function is y=0.
To learn more about vertical and horizontal asymptotes link is here
brainly.com/question/4084552
#SPJ4
The right question is:
Consider the following function. (If an answer does not exist, enter DNE.) f(x) = e^{−x^2}. Find the vertical asymptote(s). (Enter your answers as a comma-separated list.) x = Find the horizontal asymptote(s). (Enter your answers as a comma-separated list.)
y =
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP

Answers
Answer:
I cannot see the picture
Step-by-step explanation:
Jared bought 7 cans of paint. A can of red paint costs $3. 75. A can of red paint costs $2. 75. Jared spent $22 in all. How many cans of red and black paint did he buy?
Answers
Jared bought 7 cans of paint. Let the number of red paint cans that Jared bought be x. The number of black paint cans he bought would be 7 - x. A can of red paint costs $3.75 and a can of black paint costs $2.75.
He spent $22 in all. Therefore we can write:3.75x + 2.75(7 - x) = 22 Multiplying out the second term and collecting like terms gives:0.5x + 19.25 = 22Subtracting 19.25 from both sides:0.5x = 2.75Dividing by 0.5:x = 5.5Since Jared can't buy half a can of paint, we should round the answer to the nearest integer. Hence, he bought 5 cans of red paint and 2 cans of black paint. The total cost of the 5 cans of red paint would be 5 x $3.75 = $18.75.The total cost of the 2 cans of black paint would be 2 x $2.75 = $5.50.The total cost of all 7 cans of paint would be $18.75 + $5.50 = $24.25.We spent more than Jared's budget. The value of $24.25 exceeds Jared's budget of $22. Hence, there is a problem with this problem statement.
Learn more about the number here:
https://brainly.com/question/24627477
#SPJ11
find the exact values of the sine, cosine, and tangent of the angle. 255° = 300° − 45°
Answers
The exact values of the sine, cosine, and tangent of the angle 255° are -1/√2, 1/√2, and -1, respectively.
To find the exact values of the sine, cosine, and tangent of the angle 255°, we can use the identity that relates the trigonometric functions of an angle to the trigonometric functions of its complement.
By expressing 255° as the sum of 300° and -45°, we can determine the exact values of the trigonometric functions for the given angle.
We know that the sine, cosine, and tangent of an angle are periodic functions, repeating every 360 degrees. To find the exact values of the trigonometric functions for 255°, we can express it as the sum of 300° and -45°, where 300° is a multiple of 360°.
Since the sine, cosine, and tangent functions are odd or even functions, we can use the values of the trigonometric functions for 45° to determine the values for -45°.
For 45°:
sin(45°) = cos(45°) = 1/√2
tan(45°) = 1
Since cosine is an even function, cos(-45°) = cos(45°) = 1/√2.
Since sine is an odd function, sin(-45°) = -sin(45°) = -1/√2.
Using the definition of tangent as the ratio of sine to cosine, tan(-45°) = sin(-45°) / cos(-45°) = (-1/√2) / (1/√2) = -1.
Therefore, for the angle 255°:
sin(255°) = -1/√2
cos(255°) = 1/√2
tan(255°) = -1
Learn more about trigonometric functions here:
brainly.com/question/28483432
#SPJ11
Solve for y in terms of x
3x+4y-5=0
Answers
Answer:
y = \(\frac{5-3x}{4}\)
Step-by-step explanation:
3x + 4y - 5 = 0
add 5 to each side to get:
3x + 4y = 5
subtract 3x from each side to get:
4y = 5-3x
divide each side by 4 to get:
y = \(\frac{5-3x}{4}\)
C nanotubes are graphite sheets rolled up into a cylinder. This material represents one of the "hot" new research topics in chemistry. Some typical nanotubes are shown in Figure . Like the "buckyball" (graphite rolled into a ball) Carbon nanotubes have unique properties that could result in major advances in many fields including semiconductor device design and fabrication. Carbon nanotubes can be up to 70 times stronger than steel and conductivity tailored to its need. From the distance between areas of high intensity in your STM images you can calculate the internal diameter of a Carbon nanotube made up of an integer number of C atoms via the equation: D=(a(m 2
+mn+n 2
) 1n
)/π Where a represents the distance between areas of high intensity in your STM image, and n and m, are integers describing the number of C 6
rings making up the respective nanotube. On the basis of the value you have obtained, define the internal radii of nanotubes made up of 5,6 and 7 rings.
Answers
The equation D = (a(\(m^{2}\) + mn + \(n^2\))\(^(^1^/^2^)\))/π defines the internal radii of nanotubes made up of 5, 6 and 7 rings with varied values for n.
Using the equation D = (a(\(m^{2}\) + mn + \(n^2\))\(^(^1^/^2^)\))/π, we can calculate the internal diameter (D) of carbon nanotubes. The variables n and m represent integers that describe the number of carbon rings making up the respective nanotube, and a represents the distance between areas of high intensity in the STM image.
To find the internal radii of nanotubes made up of 5, 6, and 7 rings, we substitute the respective values of n and m into the equation and solve for D.
For a nanotube with 5 rings (n = 5, m = 0), the equation becomes:
D = (a(\(0^2\) + 0(5) + \(5^2\))\(^(^1^/^2^)\))/π
For a nanotube with 6 rings (n = 6, m = 0), the equation becomes:
D = (a(\(0^2\) + 0(6) + \(6^2\))\(^(^1^/^2^)\))/π
For a nanotube with 7 rings (n = 7, m = 0), the equation becomes:
D = (a(\(0^2\) + 0(7) + \(7^2\))\(^(^1^/^2^)\))/π
By solving these equations, we can determine the internal radii of carbon nanotubes made up of 5, 6, and 7 rings based on the given values of a.
Learn more about equations here:
https://brainly.com/question/14686792
#SPJ11
Construct a parallelogram whose diagonals
are 5.4 cm and 6.2 cm and an angle between
them is 70°.
Answers
Answer:
15.73 cm²
Step-by-step explanation:
Construct a parallelogram whose diagonals are 5.4 cm and 6.2 cm and an angle between them is 70°.
To construct the parallelogram, we find the Area of the parallelogram.
Area of a parallelogram = ½ × d1 × d2 × sin (y)
Where
d1 = Diagonal 1 = 5.4 cm
d2 = Diagonal 2 = 6.2 cm
y = Angle between them = 70°
Area of the parallelogram =
1/2 × 5.4 × 6.2 × sin 70
= 15.730454472 cm²
Approximately = 15.73 cm²
Kawan buys some protein bars at $0.90 each and bottled water at $0.70 each for a group hike. He buys twice as many bottles of water as protein bars. If he spends $46 in total, how many bottles of water and protein bars does he buy? Let x= the number of protein bars
Answers
Answer:
he buts 20 protein bars and 40 water bottles
Step-by-step explanation:
so first u set up an equation like this
46=.90x+.70(2x)
next you multipy
46=.90x+1.4x
Then add
46=2.3x
then divide by 2.3 to solve for x
x=20 so u have 20 protein bars
and 20 times 2 to find the amount of water bottles
Answer:
20 Protein bars and 40 waters.
Step-by-step explanation:
Let x = protein bars and y = waters
y = 2x .9x + .7 y = 46
Looking at the second equation, I would rather not work with decimals, so I will multiple the whole equation through by ten. That now gives m
9x + 7y = 460 Substitute in 2x for y (from my first equation above)
9x + 7(2x) = 460
9x +14x = 460 Combine 9x and 14x
23x = 460 Divide both sides by 23
x = 20 This is the number of protein bars. To find y plug 20 into the first equation above.
y = 2x
y =20(2)
y = 40
Divide. Write your answer as a fraction or mixed number in simplest form. 3 1/6 ÷ 4.
Please help fast.
I've tried and cant figure it out..Math isn't my specialty
Answers
Answer:
19/24
Step-by-step explanation:
Convert the mixed fraction to improper fraction:
3 1/6 = [(3 x 6) + 1] / 6 = 19/6
Convert 4 to a fraction = 4/1
So 3 1/6 ÷ 4 = 19/6 ÷ 4/1 = 19/6 x 1/4 = 19/24
How to Divide $120in the ratio 3:5
Answers
120 ÷ ( 3 + 5 ) = 120 ÷ 8 = 15
15 × 3 = 45
15 × 5 = 75
_________________________________
Answer:
15:75
Step-by-step explanation:
120 = 3x plus 5x
120 = 8x
120/8 = x
x = 15
3*15 = 45 and 5*15 = 75
find the area of the region enclosed by one loop of the curve. r = sin(4θ)
Answers
π/16 is the area enclosed by the curve r= sin(4θ)
The given curve is polar curve and hence the area of the polar curve is given by:
Let A be the area of the curve so,
A = \(\int\limits^b_a {\frac{1}{2}r^2 } \, d\theta\)
where a and b is the boundary at which r=0
so after equation r=0
sin(4θ) =0
=> sin(4θ) =0
=> 4θ = 0,π
=> θ = 0, π/4
so a=0 , b= π/4
now
A = \(\int\limits^b_a {\frac{1}{2}r^2 } \, d\theta\) ------(i)
so \(r^2\) = (sin(4θ))^2
=> \(sin^2\)( 4θ )
ans we know that
cos(2α) = 1 - \(2sin^2\)2 α
so \(sin^2\)= (1- cos(8θ) )/2
putting the value of r in the equation (i) we get :-
A = \(\int\limits^b_a {\frac{1}{4} *(1-cos8\theta) } \, d\theta\)
=> 1/4* \(\int\limits^b_a {(1-cos8\theta) } \, d\theta\)
here a=0 and b=π/4
after putting the value and solving the integral
A = π/16
so A is the area enclosed by r=sin(4θ) is π/16
To know more about polar curve click on below link:
brainly.com/question/1094340#
#SPJ4
Problem 2:
The lifespan of a particular brand of light bulb follows a normal distribution with a mean of 1000 hours and a standard deviation of 50 hours.
Find:
a) the z-score of light bulb with a mean of 500 hours.
b) If a customer buys 20 of these light bulbs, what is the probability that the average lifespan of these bulbs will be less than 980 hours?
c) the probability of light bulbs with the mean of 400 hours.
d) the number of light bulbs with the mean less than 1000 hours
Answers
The answers are:
a) The z-score for a light bulb that lasts 500 hours is -10.
b) For a sample of 20 light bulbs, the probability that the average lifespan will be less than 980 hours is approximately 0.0367, or 3.67%.
c) The z-score for a light bulb that lasts 400 hours is -12. This is even more unusual than a lifespan of 500 hours.
d) Given the lifespan follows a normal distribution with a mean of 1000 hours, 50% of the light bulbs will have a lifespan less than 1000 hours.
How to solve the problema) The z-score is calculated as:
z = (X - μ) / σ
Where X is the data point, μ is the mean, and σ is the standard deviation. Here, X = 500 hours, μ = 1000 hours, and σ = 50 hours. So,
z = (500 - 1000) / 50 = -10.
The z-score for a bulb that lasts 500 hours is -10. This is far from the mean, indicating that a bulb lasting only 500 hours is very unusual for this brand of bulbs.
b) If a customer buys 20 of these light bulbs, we're now interested in the average lifespan of these bulbs. . In this case, n = 20, so the standard error is
50/√20
≈ 11.18 hours.
z = (980 - 1000) / 11.18 ≈ -1.79.
The probability that z is less than -1.79 is approximately 0.0367, or 3.67%.
c) The z-score for a bulb with a lifespan of 400 hours can be calculated as:
z = (400 - 1000) / 50 = -12.
The probability associated with z = -12 is virtually zero. So the probability of getting a bulb with a mean lifespan of 400 hours is virtually zero.
d) The mean lifespan is 1000 hours, so half of the light bulbs will have a lifespan less than 1000 hours. Since the lifespan follows a normal distribution, the mean, median, and mode are the same. So, 50% of light bulbs will have a lifespan less than 1000 hours.
Read more on probability here:https://brainly.com/question/13604758
#SPJ1
Multiply the starting price by the right term that uses the compound average to show that the arithmetic mean does not recover the final price while the geometric and continuous means do. Convert the percent averages to fractions.
$53. 07 x (1 + arith mean) 3 = 53.07 x (1 + #21 %) 3 = #22
$53. 07 x (1 + geom mean) 3 = 53.07 x (1 + #23 %) 3 = $ #24
$53. 07 x e cont mean x 3 = 53.07 x e #25 % x 3 = $ #26
I need help filling out numbers #21 through #26
Answers
The values for numbers #21 through #26 are as follows:
#21: 2.33% or 0.0233. #22: $56.4842. #23: 1.85% or 0.0185. #24: $56.4148. #25: 3.64% or 0.0364. #26: $57.4397
#21: 2.33% (arithmetic mean as a fraction: 0.0233)
#22: $56.4842 (result of the calculation)
#23: 1.85% (geometric mean as a fraction: 0.0185)
#24: $56.4148 (result of the calculation)
#25: 3.64% (continuous mean as a fraction: 0.0364)
#26: $57.4397 (result of the calculation)
To fill out numbers #21 through #26, we need to calculate the values for each term using the given information and convert the percentages to fractions.
#21: The arithmetic mean is given as a percentage. Convert it to a fraction by dividing by 100. Therefore, #21 = 2.33% = 0.0233.
#22: Multiply the starting price ($53.07) by the compound factor (1 + arithmetic mean)^3. Substitute the value of #21 into the calculation. Therefore, #22 = $53.07 x (1 + 0.0233)^3 = $56.4842.
#23: The geometric mean is given as a percentage. Convert it to a fraction by dividing by 100. Therefore, #23 = 1.85% = 0.0185.
#24: Multiply the starting price ($53.07) by the compound factor (1 + geometric mean)^3. Substitute the value of #23 into the calculation. Therefore, #24 = $53.07 x (1 + 0.0185)^3 = $56.4148.
#25: The continuous mean is given as a percentage. Convert it to a fraction by dividing by 100. Therefore, #25 = 3.64% = 0.0364.
#26: Multiply the starting price ($53.07) by the continuous factor e^(continuous mean x 3). Substitute the value of #25 into the calculation. Therefore, #26 = $53.07 x e^(0.0364 x 3) = $57.4397.
Hence, the values for numbers #21 through #26 are as calculated above.
To learn more about fraction, click here: brainly.com/question/28372533
#SPJ11
What are the coordinates of point P on the directed line segment from A to B such that P is One-fourth the length of the line segment from A to B?
Answers
Answer:
The answer is explained below
Step-by-step explanation:
The location of point A = (-5, -1) and point B = (4, 1).
To find the coordinate of the point that divides a line segment PQ with point P at \((x_1,y_1)\) and point Q at \((x_2,y_2)\) in the proportion a:b, we use the formula for the x and y coordinates:
\(x-coordinate:\\\frac{a}{a+b}(x_2-x_1)+x_1 \\\\While \ for\ y-coordinate:\\\frac{a}{a+b}(y_2-y_1)+y_1\)
P is One-fourth the length of the line segment from A to B, Therefore AB is divided in the ratio 1:4. The location of point A = (-5, -1) and point B = (4, 1).Therefore:
\(x-coordinate:\\\frac{1}{1+3}(4-(-5))+(-5)=\frac{1}{4}(9)-5=-\frac{11}{4} \\\\While \ for\ y-coordinate:\\\frac{1}{1+3}(1-(-1))+(-1)=\frac{1}{4}(2)-1=\frac{-1}{2}\)
Therefore the coordinate of P is (-11/4, -1/2)
Answer:
the coordinate of P is (-11/4, -1/2)
x= -11/4
y= -1/2
c on edu
Step-by-step explanation:
edu 2021
if you place a 37 foot ladder against the top of a 12 foot building, how many felt will the bottom of the ladder be from the bottom of the building
Answers
Answer:
Would it be 25 that’s what I got
Step-by-step explanation: