For security purposes I regularly change my six-digit passcode for internet banking. I always
choose a code that is made up of three different two-digit square numbers (i. E. Square numbers
between 10 and 99), with the sixth digit the same as the first digit.
-Which two digits never appear in any of my passcodes?
-How many different passcodes can I use?
The sum of the six digits of my current passcode is also a square number.
-What is my current passcode?
Answers
The two digit Combinations that never appear in any of the passcodes are 5 and 6.
There are 49 different passcodes that can be used. The sum of the six digits of the current passcode is 81, which is a square number. Therefore, the current passcode is made up of three different two-digit square numbers with the sum of their digits equal to 9.
The possible combinations are
(16, 25, 40),
(16, 49, 16),
(25, 36, 20),
(36, 49, 4),
(49, 64, 9),
(64, 81, 16), and
(81, 16, 64).
The only combination that has the same first and sixth digits is (16, 25, 40), so the current passcode is 162540.
Learn more about Combinations
https://brainly.com/question/4658834
#SPJ4
Related Questions
At LaGuardia Airport for a certain nightly flight, the probability that it will rain is 0.15 and the probability that the flight will be delayed is 0.11. The probability that it will not rain and the flight will leave on time is 0.75. What is the probability that the flight would be delayed when it is raining? Round your answer to the nearest thousandth.
Answers
If At LaGuardia Airport for a certain nightly flight. The probability that the flight would be delayed when it is raining is: 0.140.
What is the probability?First step is to find the P(rain and on time)
P(rain and on time) = 1 - P(not rain and on time)
P(rain and on time) = 1 - 0.75
P(rain and on time)= 0.25
Now we can calculate P(delay and rain):
P(delay and rain) = P(delay | rain) * P(rain)
= P(rain and on time) - P(not rain and on time)
= 0.25 - 0.11
= 0.14
Therefore the probability that the flight would be delayed is 0.140 .
Learn more about probability here:https://brainly.com/question/13604758
#SPJ1
Find the area of the region enclosed by the curves. 10 X= = 2y² +12y + 19 X = - 4y - 10 2 y=-3 5 y=-2 Set up Will you use integration with respect to x or y?
Answers
The area of the region enclosed by the curves 10x=2y²+12y+19 and x=-4y-10 is 174/3 units².
To find the area of the region enclosed by the curves 10x=2y²+12y+19 and x=-4y-10, we need to solve this problem in the following way:
Since the curves are already in the form of x = f(y), we need to use vertical strips to find the area.
So, the integral for the area of the region is given by:
A = ∫a b [x₂(y) - x₁(y)] dy
Here, x₂(y) = 10 - 2y² - 12y - 19/5 = - 2y² - 12y + 1/2 and x₁(y) = -4y - 10
So,
A = ∫(-3)⁻²[(-2y² - 12y + 1/2) - (-4y - 10)] dy + ∫(-2)⁻²[(-2y² - 12y + 1/2) - (-4y - 10)] dy
=> A = ∫(-3)⁻²[2y² + 8y - 19/2] dy + ∫(-2)⁻²[2y² + 8y - 19/2] dy
=> A = [(2/3)y³ + 4y² - (19/2)y]₋³ - [(2/3)y³ + 4y² - (19/2)y]₋² | from y = -3 to -2
=> A = [(2/3)(-2)³ + 4(-2)² - (19/2)(-2)] - [(2/3)(-3)³ + 4(-3)² - (19/2)(-3)]
=> A = 174/3
Hence, the area of the region enclosed by the curves is 174/3 units².
Know more about area here:
https://brainly.com/question/15122151
#SPJ11
What is the length of the missing leg?
17 mm
15 mm
Answers
Answer:
17 mm + 15mm = 32
Step-by-step explanation:
Find the value of x?

Answers
Answer:
14
Step-by-step explanation:
This is a special type of right triangle called a 45 45 90
The sides have length a and the hypotenuse has length a* sqrt(2)
a = 7 sqrt(2)
the hypotenuse has length x
x = 7 sqrt(2) * sqrt(2)
x = 7 *2
x = 14
What is the degree of 5xpower2+6xpower2+7ypower2
Answers
Answer:
7
Step-by-step explanation:
Explanation:
6x5+5x4−3x2+x7
Michael has v sweets.
Lily has 5 more sweets than Michael.
James has 8 more sweets than Lily.
They have 75 sweets altogether.
Find the number of sweets Michael has.
Answers
Answer:
lily - 5
5+8= 13
James - 13
13+5= 18
18-75= 57
Michael - 57
A) Determine the values of 'a' and 'd'
b) Determine the explicit formula for the sequence. \
c) Determine t20

Answers
The explicit formula is tn = -1/3 + 2/3(n - 1) and the value of t20 is 37/3
How to determine the explicit formula?The terms of the sequence are given as:
t2 = 1/3
t8 = 13/3
An arithmetic sequence is represented as:
tn = a + (n - 1)d
So, we have:
t2 = a + d
t8 = a + 7d
This implies that
a + d = 1/3
a + 7d = 13/3
Subtract the equations
6d = 12/3
Solve for d
d = 2/3
Substitute d = 2/3 in a + d = 1/3
a + 2/3 = 1/3
Solve for a
a = -1/3
Substitute d = 2/3 and a = -1/3 in tn = a + (n - 1)d
tn = -1/3 + 2/3(n - 1)
Hence, the explicit formula is tn = -1/3 + 2/3(n - 1)
The value of t20
This means that n = 20.
So, we have:
t20 = -1/3 + 2/3(20 - 1)
Evaluate
t20 = 37/3
Hence, the value of t20 is 37/3
Read more about arithmetic sequence at:
https://brainly.com/question/6561461
#SPJ1
Plshelp
find a10 in sequence 3, 1, 1/3, 1/9
Answers
Answer:
1/2187 is the 10th answer in the sequence
Step-by-step explanation:
just keep dividing the number by 3
1/9, 1/27, 1/81, 1/243, 1/729, 1/2187
Last year, Boris biked n miles. This year, he biked 281 miles. Using n, write an expression for the total number of miles he biked.
Answers
Answer:
we can't add a letter and a number so we leave it as shown in the picture above.
hope it helps.

The midpoint of AB is M(-5, 1). If the coordinates of A are (-4,-5), what are
the coordinates of B?
Answers
Answer:
-6, 7
Step-by-step explanation:
Answer: B(-6,7)
Step-by-step explanation:
M(-5, 1) A(-4,-5) B(x,y)=?
\(\displaystyle\\M_x=\frac{x_A+x_B}{2} \\\\-5=\frac{-4+x_B}{2}\\\\\)
Multiply both parts of the equation by 2:
\(-5(2)=-4+x_B\\\\-10=-4+x_B\\\\-10+4=-4+x_B+4\\\\-6=x_B\\\\Thus,\ x_B=-6\)
\(\displaystyle\\\\\\1=\frac{-5+y_B}{2} \\\\\)
Multiply both parts of the equation by 2:
\(1(2)=-5+y_B\\\\2=-5+y_B\\\\2+5=-5+y_B+5\\\\7=y_B\\\\Thus,\ y_B=7\)
Find the slope of the line that passes through (4,-5) and (-2,9)
a -2/3
b 5/3
c-7/3
d 2
Please help me ASAP
Answers
Answer:
sorry i dont know
Hope this helps
Does anyone know the answer or how you're supposed to answer this?


Answers
Answer:
Step-by-step explanation:
(a) Triangle possible because 5 + 12 > 13.
(b) Triangle possible because the 3 angles add up to 180 degrees.
(c) No Triangle possible because 5 + 2 < 8.
(d) Triangle possible because the 3 angles add up to 180 degrees.
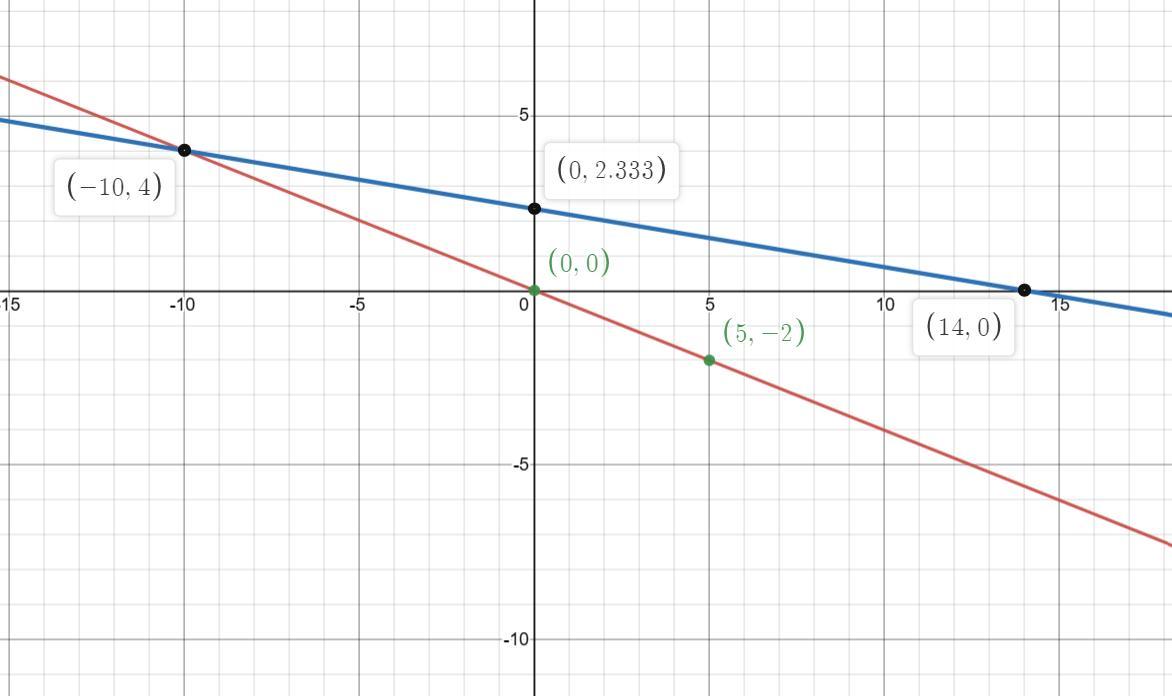
Solve the system graphically and check x+2y the solution.2x+5y=0. X+6y=14
Answers
Given:
The system of the equation is,
\(\begin{gathered} 2x+5y=0 \\ x+6y=14 \end{gathered}\)Draw the lines on the graph, the point at which the lines intersects. That point will be the solution of the system.
The points on the line 2x+5y=0 are,
\(\begin{gathered} 2x+5y=0 \\ x=0\Rightarrow y=0 \\ x=5\Rightarrow y=-2 \\ x=-10\Rightarrow y=4 \end{gathered}\)And the points on the line x+6y=14
\(\begin{gathered} x+6y=14 \\ x=0\Rightarrow y=\frac{7}{3} \\ x=14\Rightarrow y=0 \\ x=-10\Rightarrow y=4 \end{gathered}\)The graph of the lines is,
As the point of intersection is ( -10,4).
The solution of the given system of equation is x = -10, y = 4.
Please help with this question, thanks.

Answers
Answer:
<ADB=<CBD
Step-by-step explanation:
it says bisect, meaninf that the angle is split in 2 equal prats, thus the angles are the same size.
What is the relationship between a 90% confidence interval around a mean and a 95% confidence interval around a mean?.
Answers
Answer: With a 95 percent confidence interval, you have a 5 percent chance of being wrong. With a 90 percent confidence interval, you have a 10 percent chance of being wrong. A 99 percent confidence interval would be wider than a 95 percent confidence interval (for example, plus or minus 4.5 percent instead of 3.5 percent)
Step-by-step explanation:
Suppose that 10% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 thalts, and let X denote the number among these that are nonconforming and can be reworked. (Round your answers to four decimal places) (a) What is the approximate) probability that is at most 302 (b) What is the approximate probability that is less than 107 (c) What is the approximate probability that is between 1 and 25 (inclusive)
Answers
the approximate probability that is at most 302 is 0, the approximate probability that is less than 107 is 1, and the approximate probability that is between 1 and 25 (inclusive) is 0.9219.
Suppose that 10% of all steel shafts produced by a certain process are nonconforming but can be reworked (rather than having to be scrapped). Consider a random sample of 200 thalts, and let X denote the number among these that are nonconforming and can be reworked. We are to find the approximate probability that X is at most 302, less than 107, and between 1 and 25 (inclusive).
Here, p = 0.10, q = 1 - p = 0.90, n = 200.
The probability that X is at most 302:
We can use the normal distribution to find this probability. The sample size is large, and the population proportion is known. The mean and variance of the binomial distribution are given by:
μ = np = 200 × 0.10 = 20
σ² = npq = 200 × 0.10 × 0.90 = 18
The normal distribution has a mean of μ = 20 and a standard deviation of σ = 4.2426 (square root of σ²). The z-score corresponding to X = 302 is:
z = (302 - 20) / 4.2426 = 69.97
Using a standard normal table or calculator, we find that the probability of Z ≤ 69.97 is essentially zero (to four decimal places). Therefore, the approximate probability that X is at most 302 is 0.
The probability that X is less than 107:
Using the same approach as in part (a), we have:
μ = np = 200 × 0.10 = 20
σ² = npq = 200 × 0.10 × 0.90 = 18
The z-score corresponding to X = 107 is:
z = (107 - 20) / 4.2426 = 19.53
The probability of Z ≤ 19.53 is very close to 1 (to four decimal places). Therefore, the approximate probability that X is less than 107 is 1.
The probability that X is between 1 and 25 (inclusive):
Here, we need to find the probability of 0 < X < 26. We can use the normal distribution as an approximation to the binomial distribution. The mean and standard deviation of X are:
μ = np = 200 × 0.10 = 20
σ = sqrt(npq) = sqrt(200 × 0.10 × 0.90) = 4.2426
The z-scores corresponding to X = 0 and X = 26 are:
z1 = (0 - 20) / 4.2426 = -4.714
z2 = (26 - 20) / 4.2426 = 1.414
Using a standard normal table or calculator, we find that the probability of Z ≤ -4.714 is essentially zero, and the probability of Z ≤ 1.414 is approximately 0.9219. Therefore, the approximate probability that X is between 1 and 25 (inclusive) is:
P(0 < X < 26) ≈ P(-4.714 < Z < 1.414) ≈ 0.9219 - 0 = 0.9219.
for more questions on probability
https://brainly.com/question/24756209
#SPJ11
As the prize in a contest, you are offered $29,000 now or $51,000 in 6 years. If the money can be invested at 9% compounded annually, which prize will be worth more in 6 years? Choose the option that is most profitable after 6 years. O accepting the $29,000 prize now O accepting the $51,000 prize in 6 years
Answers
If the money can be invested at 9% compounded annually, then accepting the $51,000 prize in 6 years is the most profitable option after 6 years.
First, let's calculate the future value of the $29,000 prize if it is invested at 9% annual compounded rate for 6 years. We can use the formula FV = PV * (1 + r)^n, where FV is the future value, PV is the present value, r is the annual interest rate, and n is the number of compounding periods. In this case, PV is $29,000, r is 9%, and n is 6. Plugging these values into the formula, we get FV = $29,000 * (1 + 0.09)^6 = $49,193.29.
Now, let's calculate the future value of the $51,000 prize if it is received in 6 years. We already know that the money can be invested at 9% annual compounded rate for 6 years. So, we can directly use the formula FV = PV * (1 + r)^n. In this case, PV is $51,000, r is 9%, and n is 6. Plugging these values into the formula, we get FV = $51,000 * (1 + 0.09)^6 = $86,929.63.
Comparing the future values of both options, we can see that accepting the $51,000 prize in 6 years is more profitable as it will result in a future value of $86,929.63, which is higher than the future value of $49,193.29 that would result from investing the $29,000 prize now.
In conclusion, if the money can be invested at 9% compounded annually, then accepting the $51,000 prize in 6 years is the most profitable option after 6 years. It is important to note that this decision is based solely on financial considerations, and other non-financial factors may also be relevant when making such decisions.
For more such questions on Prize-Profit Comparison.
https://brainly.com/question/14850973#
#SPJ11
After all of the start-up costs, a company starts with $100 and makes $0.75 on each unit sold. Write a linear equation in slope intercept form that models this situation using P for profit and N for number of units sold.
A). p=100n+75
B). n=100p+75
C). p=0.75n+100
D). n=0.75p+100
If you guys could help me I would greatly appreciate it!!
Answers
The answer would most likely be c because you multiply 0.75 by the amount of units sold and find out the profit after adding it.
Hope this helps! :)
Formalize the following in terms of atomic propositions r, b, and w, first making clear how they correspond to the
English text. (a) Berries are ripe along the path, but rabbits have not been seen in the area.
(b) Rabbits have not been seen in the area, and walking on the path is safe, but berries are ripe along the path.
(c) If berries are ripe along the path, then walking is safe if and only if rabbits have not been seen in the area.
(d) It is not safe to walk along the path, but rabbits have not been seen in the area and the berries along the path are ripe.
e) For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to
pave been seen in the area.
Walking is not safe on the path whenever rabbits have been seen in the area and berries are ripe along the path.
Answers
Walking is not safe on the path whenever rabbits have been seen in the area, and berries are ripe along the path. This is formalized by using the →(if-then) and ∧(logical and) operators.
Given information and corresponding atomic propositions:
We need to formalize the given statements in terms of atomic propositions r, b, and w, which are defined as follows:
r: Rabbits have been seen in the area.
b: Berries are ripe along the path.
w: Walking on the path is safe.
Now, let us formalize each of the given statements in terms of these atomic propositions:
a) Berries are ripe along the path, but rabbits have not been seen in the area.
b: Rabbits have not been seen in the area, and walking on the path is safe, but berries are ripe along the path.
c: If berries are ripe along the path, then walking is safe if and only if rabbits have not been seen in the area.
d: It is not safe to walk along the path, but rabbits have not been seen in the area, and the berries along the path are ripe.
e) For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to have been seen in the area.
Walking is not safe on the path whenever rabbits have been seen in the area, and berries are ripe along the path.
The formalizations in terms of atomic propositions are:
a) b ∧ ¬r.b) ¬r ∧ w ∧
b.c) (b → w) ∧ (¬r → w).
d) ¬w ∧ ¬r ∧
b.e) (¬r ∧ ¬b) → w.b ∧
Berries are ripe along the path, but rabbits have not been seen in the area.
This is formalized by using the ∧(logical and) operator.
(¬r ∧ ¬b) → w: It means For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to have been seen in the area.
For more related questions on area:
https://brainly.com/question/1631786
#SPJ8
Use pumping Lemma to prove that the following languages are not regular L3={ωωRβ∣ω,β∈{0,1}+} . L4={1i0j1k∣i>j and i0}
Answers
The language L3 is not regular. It can be proven using the pumping lemma for regular languages.
Here is the proof:
Assume L3 is a regular language.
Let w = xyβ, where β is a non-empty suffix of ω and x is a prefix of ω of length p or greater.
We can write w as w = xyβ = ωαββ R, where α is the suffix of x of length p or greater. Because L3 is a regular language, there exists a string v such that uviw is also in L3 for every i ≥ 0.
Let i = 0.
Then u0viw = ωαββR is in L3. By the pumping lemma, we have that v = yz and |y| > 0 and |uvyz| ≤ p. But this means that we can pump y any number of times and still get a string in L3, which is a contradiction.
Therefore, L3 is not a regular language.
To know more about language visit:
https://brainly.com/question/32089705
#SPJ11
Select the inequality that match the situation:
A school fundraiser has a minimum target of $500. Faculty have donated $100 and there
are 12 student clubs that are participating with different activities. How much money
should each club raise to meet the fundraising goal?
12x - 100 > 500
12x +100 > 500
12x- 100 > 500
12x + 100 > 500
12x - 100 < 500
12x + 100 < 500
Answers
Answer:
Each student club must contribute $ 33.33 in order to meet the fundraising goal.
Step-by-step explanation:
Given that a school fundraiser has a minimum target of $ 500. Faculty have donated $ 100 and there are 12 student clubs that are participating with different activities, to determine how much money should each club raise to meet the fundraising goal, the following calculation must be performed:
(500 - 100) / 12 = X
400/12 = X
33,333 = X
Thus, each student club must contribute $ 33.33 in order to meet the fundraising goal.
The Robinson family and the Moore family are going on a day trip to visit the Square Caverns on Monday. The Robinson family has 2 parents and 4 children and paid $75 for admission. The Moore family has 2 parents and 3 children and paid $60. If x represents the admission price of each parent and y represents the admission price of each child, which is a system of equations that could be used to determine the admission price of an adult ?
Answers
Answer:
admission price of each parent = $7.5
admission price of each child = $15
Step-by-step explanation:
x = admission price of each parent
y = admission price of each child
Robinson family:
2x + 4y = 75
Moore family:
2x + 3y = 60
2x + 4y = 75 (1)
2x + 3y = 60 (2)
Subtract (2) from (1)
4y - 3y = 75 - 60
y = 15
Substitute y = 15 into (1)
2x + 4y = 75
2x + 4(15) = 75
2x + 60 = 75
2x = 75 - 60
2x = 15
x = 15/2
x = 7.5
witch rational number is between -11/15 and -5/6?
answers to chose from -1, -7/10, -4/5 and -13/15
Answers
Answer:
-4/5
Step-by-step explanation:
To find this we can look for the \(LCD\) between all the numbers
Here are our \(LCD's\) (Least Common Denominator)
-22/30 and -25/30
It wouldn't be -1 because it isn't in between those numbers
It isn't -7/10 because if we turn it into our \(LCD\) it would be -21/30 which isn't in between those numbers
It is -4/5 because if we turn in into our \(LCD\) it would be -24/30 which is between those numbers
This means we have our right answer we know our last one is incorrect
Find the slope of the line that is (a) parallel and (b) perpendicular to the line through the pair of points. (−5,−4) and (3,5)
Answers
An \( \bar{X} \) chart is used to track a process with binary outcome variables. True or False
The reasons for holding inventory include all the following EXCEPT Multiple Choice it serves as a buffer
Answers
The statement is false. A process chart is a graphical tool used to monitor processes in production and service industries. The average process performance and the upper and lower limits are calculated and displayed on an X-bar chart, which is a common process chart.
An \( \bar{X} \) chart is NOT used to track a process with binary outcome variables. The statement is false.
Explanation: A process chart is a graphical tool used to monitor processes in production and service industries. The average process performance and the upper and lower limits are calculated and displayed on an X-bar chart, which is a common process chart. The values for a variable can be collected and analyzed using process charts. An \( \bar{X} \) chart, commonly known as an x-bar chart, is used to monitor a process with continuous numerical data. A binary outcome variable, on the other hand, has only two possible outcomes (e.g., yes/no, pass/fail, etc.). As a result, binary data is unsuitable for an \( \bar{X} \) chart, which is only used to monitor continuous numerical data.
Variables are values that may be altered in a process, which can affect its results. Variables may be categorized as continuous or discrete, depending on whether they can be measured or counted. Discrete variables, such as the number of employees working on a task or the number of items produced in a process, are quantifiable and can be measured precisely. Continuous variables, such as the temperature, length, or weight, can take on any value over a range and are therefore less specific. The reasons for holding inventory include serving as a buffer against uncertainties, ensuring product availability and preventing stockouts, reducing lead times and transportation costs, taking advantage of discounts and bulk purchasing opportunities, and providing a hedge against inflation and price fluctuations.
To know more about X-bar chart visit: https://brainly.com/question/31861365
#SPJ11
lauren makes $36 an hour. she gets a 10% raise. she works 40 hours a week. how much more money will she make this week as a result of her raise?
Answers
Answer:
$1584
Step-by-step explanation:
T/F The interquartile range IQR is found by subtracting the mean from the maximum value of a data set.
Answers
The IQR is calculated as the difference between the 75th and 25th percentiles of a dataset. It is not found by subtracting the mean from the maximum value of the dataset.
What is data?Data is the collection of data term that is organized and formatted in a specific way it typically contains fact observations or statistics that are collected through a process of measurement or research data set can be used to answer the question and help make an informed decision they can be used in a variety of ways such as to identify trends on cover patterns and make a prediction.
According to the given information:The interquartile range (IQR) is a statistical measure used to describe the spread or dispersion of a dataset. It is calculated as the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of the dataset. In other words, the IQR represents the range of the middle 50% of the data.
To calculate the IQR, you first need to determine the median of the dataset. The median is the middle value of the dataset when it is arranged in order from smallest to largest. Then, you divide the dataset into two halves based on this median value: the lower half (values smaller than the median) and the upper half (values larger than the median).
Next, you determine the median of each of these halves separately. The median of the lower half is the first quartile (Q1), and the median of the upper half is the third quartile (Q3).
Finally, the IQR is calculated as the difference between Q3 and Q1 (IQR = Q3 - Q1).
So, to sum up, the IQR is not found by subtracting the mean from the maximum value of a dataset, but instead by calculating the difference between the 75th and 25th percentiles of the dataset.
Therefore, The IQR is calculated as the difference between the 75th and 25th percentiles of a dataset. It is not found by subtracting the mean from the maximum value of the dataset.
To know more about data click-
brainly.com/question/14592520
#SPJ1
Jesse now has $200 and his goal is to buy a bicycle that costs $375. He earns $10 for every car that he washes. Write an inequality that represents the number of cars Jesse must wash in order to afford the bicycle. Then, solve the inequality to determine the number of cars Jesse must wash in order to afford the bicycle. Show all of your work and remember to include units.
Answers
x = 17.5, but round up to 18 because you can’t wash half of a car
Answer:
$200 + $10x = $375
Well we're going to round up to $380, cause their making money in increments of 10 rather than 5.
And based off that I'd subtract $375 from $200 (375 -200 = 180)
Then take that answer and divide it by 10. (180 / 10)
Jesse will need to wash at least 18 more cars in order to afford the bicycle
Select the expression that results in a rational number.

Answers
The correct answer is A.\(\((5 \frac{1}{\overline{9}}) \times (-0.\overline{3})\)\), as it involves the multiplication of two rational numbers, resulting in a rational number.
The expression that results in a rational number is A. \(\((5 \frac{1}{\overline{9}}) \times (-0.\overline{3})\)\). To determine if an expression yields a rational number, we need to check if it involves the multiplication of two rational numbers. In option A, \(\(5 \frac{1}{\overline{9}}\)\) represents a mixed fraction, which can be expressed as the sum of a whole number and a fraction, both of which are rational. Similarly, \(\(-0.\overline{3}\)\) is a repeating decimal, which can be expressed as a fraction, also a rational number.Therefore, the product of these two rational numbers in option A will yield a rational number.
For more questions on rational numbers:
https://brainly.com/question/19079438
#SPJ8
Rate of Commission" refers to the amount sold. True or false
Answers
Answer:
False
mind giving me brainliest im on my way to ace, thanks!
Step-by-step explanation: