For a normal distribution mean is _______ to median.
Answers
Related Questions
Find the local maxima, local minima, and saddle points, if any, for the function z = 3x3 – 36xy – 3y3. (Use symbolic notation and fractions where needed. Give your answer as point coordinates in t
Answers
Answer:
(0,0) is a saddle point
(-4,4) is a local maximum
Step-by-step explanation:
\(\displaystyle z=3x^3-36xy-3y^3\\\\\frac{\partial z}{\partial x}=9x^2-36y\\\\\frac{\partial z}{\partial y}=-36x-9y^2\)
Determine critical points
\(9x^2-36y=0\\9x^2=36y\\\frac{x^2}{4}=y\)
\(-36x-9y^2=0\\-36x-9(\frac{x^2}{4})^2=0\\-36x-\frac{9}{16}x^4=0\\x(-36-\frac{9}{16}x^3)=0\\\\x=0\\\\-36-\frac{9}{16}x^3=0\\-36=\frac{9}{16}x^3\\-64=x^3\\-4=x\)
When x=0
\(9x^2-36y=0\\9(0)^2-36y=0\\-36y=0\\y=0\)
When x=-4
\(9x^2-36y=0\\9(-4)^2-36y=0\\9(16)-36y=0\\144-36y=0\\144=36y\\4=y\)
So, we need to check what kinds of points (0,0) and (-4,4) are.
For (0,0)
\(\displaystyle H=\biggr(\frac{\partial^2 z}{\partial x^2}\biggr)\biggr(\frac{\partial^2 z}{\partial y^2}\biggr)-\biggr(\frac{\partial^2 z}{\partial x\partial y}\biggr)^2\\\\H=(18x)(-18y)-(-36)^2\\\\H=(18(0))(-18(0))-(-36)^2\\\\H=-1296 < 0\)
Therefore, (0,0) is a saddle point since \(H < 0\).
For (-4,4)
\(\displaystyle H=\biggr(\frac{\partial^2 z}{\partial x^2}\biggr)\biggr(\frac{\partial^2 z}{\partial y^2}\biggr)-\biggr(\frac{\partial^2 z}{\partial x\partial y}\biggr)^2\\\\H=(18x)(-18y)-(-36)^2\\\\H=(18(-4))(-18(4))-(-36)^2\\\\H=(-72)(-72)-1296\\\\H=5184-1296\\\\H=3888 > 0\)
Because \(H > 0\) and since \(\frac{\partial^2z}{\partial x^2}=-72 < 0\), then (-4,4) is a local maximum
Given the sequence 10, 20, 40, 80,.... find 25th term
Answers
The formula for a geometric sequence is: ar to the power of n-1
A= first term and r= the factor between the terms (called the common ratio)
Now we juss input it in the formula
10 x 2 to the power of n-1
Now we want to work out the 25th term so n=25 we do 25-1=24
So it’s 10*2 to the power of 24
Answer: 167772160
Hope this helped
Answer:
167,772,160
Step-by-step explanation:
-Each term is multiplied by 2-
10, 20, 40, 80, 160, 320, 640, 1,280, 2,560, 5,120, 10,240, 20,480, 40,960, 81,920, 163,840, 327,680, 655,360, 1,310,720, 2,621,440, 5,242,880, 10,485,760, 20,971,520, 41,943,040, 83,886,080, 167,772,160
167,772,160 is the 25th term
Write the inverse of the given conditional statement

Answers
Answer:
If I live in South Carolina then I live in Charleston
Step-by-step explanation:
Just switch them
Which equation best represents the relationship between x and y in the paragraph
Y=3x-2
Y=-1/2x+3
Y=-2x+3
Y=2x+3/2

Answers
The link between x and y in the paragraph is best illustrated by the equation y=-2x+3.
A formula that demonstrates the relationship between the expressions on either side of a sign. That typically has an equal sign and one variable. When it is necessary to combine two or more components in order to comprehend or adequately explain a situation, an equation is used. It can occasionally be challenging to distinguish between an equation and a formula since both contain equals signs. Calculations for specific purposes, such as converting from Fahrenheit and Celsius or vice versa, are known as formulas. No matter what values are used, a formula is also always accurate.
The graph shows that the line passes through points (0, 3) and (3/2, 0).
Assumption: y= kx + b
k=3-0/0-3/2=-2
b= 3
Therefore, y= -2x + 3
Learn more about equation here
https://brainly.com/question/25678139
#SPJ1
Quadrilateral ABCD is inscribed in a circle. If angle B measures 24°, what is the measure of angle D?
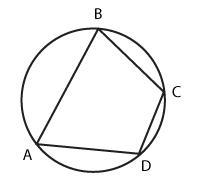
Answers
Answer: 156!
Step-by-step explanation: i’m not going to lie, i guessed but, i ended up getting it right .
Find m
Geometry help pls

Answers
Answer:
∠WXY=72°
Step-by-step explanation:
2X-2=70+X
2X-X=70+2
X=72° ⇒ ∠WXY=72°
FIND ANDGLE RPQ
THE NUMBER ON TOP IS 98 and the bottom is 110

Answers
Answer:
152
Step-by-step explanation:
this is because there is 360 degrees in a circle and if you subtract 98 and 110 from 360 you get 152.
Determine the numbers of solutions for 18x - 12 = 3(6x – 12).
Answers
I think
I am sure
Answer:
the statement is false
Step-by-step explanation:
\(18x - 12 = 3(6x - 12) \\ 18x - 12 = 18x - 36 \\ \)
\( - 12 = - 36\)
Can a triangle be formed with side lengths 4, 8, 11? Explain. No, because 11 − 8 < 4 Yes, because 11 − 4 < 8 No, because 4 + 8 > 11 Yes, because 4 + 8 > 11
Answers
A triangle can be formed with side lengths 4, 8, 11. Yes, because 4 + 8 > 11
How to illustrate the triangle?According to the Triangle Inequality Theorem, the largest side cannot be greater than the sum of the other two sides. The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the remaining side.
If the sum of any two sides is greater than the sum of the third, then the difference of any two sides is less than the sum of the third. The sum of any two sides must be greater than the sum of the third. The longest side in a triangle is the side opposite a larger angle.
Learn more about triangles on:
https://brainly.com/question/17335144
#SPJ1
what condition or conditions must hold true for the sampling distribution of the sample mean to be normal when the sample size is less than 30?
Answers
When the sample size is smaller than 30, the following requirements must be met for the sampling distribution of the sample mean to be considered normal:
The data values should be symmetrical in the sample.No outliers should be in sample data .If these conditions are satisfied then the sampling distribution of the sample mean to be normal when sample size is less than 30.
A statistic's sampling distribution is a form of probability distribution produced by selecting several random samples of a predetermined size from the same population. You may better comprehend the variations in a sample statistic by using these distributions.
Learn more about Sampling distribution at,
https://brainly.com/question/13668062
#SPJ4
find the net change in the value of the function between the given inputs. f(x) = 6x − 5; from 1 to 6
Answers
The net change in the value of the function between x = 1 and x = 6 is 30.
To find the net change in the value of the function between the inputs of 1 and 6, we need to find the difference between the output values of the function at x = 1 and x = 6, and then take the absolute value of that difference.
First, we can find the output value of the function at x = 1:
f(1) = 6(1) - 5 = 1
Next, we can find the output value of the function at x = 6:
f(6) = 6(6) - 5 = 31
The net change in the value of the function between x = 1 and x = 6 is the absolute value of the difference between these two output values:
|f(6) - f(1)| = |31 - 1| = 30
Therefore, the net change in the value of the function between x = 1 and x = 6 is 30.
To learn more about net change visit: https://brainly.com/question/29989249
#SPJ11
express the following shaded area using a definite integral. use geometry to calculate the area. please show work too

Answers
Answer:
Integrate( sqrt(9-x^2) from x=-3 to x=3)
Step-by-step explanation:
The equation for a full circle is (x-h)^2+(y-k)^2=r^2 where (h,k) is center and radius is r.
Your center, your (h,k) is (0,0). Your radius, your r, is 3.
So your equation is (x-0)^2+(y-0)^2=3^2 or more simply x^2+y^2=9.
We also must consider we don't have full circle.
Solving for y will give us the circle in terms of top half if we take positive values and bottom half if we take negative values. Since y is positive in the picture, you only see top half, we will only take the positive cases for y.
Subtracting x^2 on both sides gives: y^2=9-x^2
Square root both sides: y= sqrt(9-x^2)
(I did not choose -sqrt(9-x^2) because again y is positive).
So the x's in the picture range from -3 to 3.
The integral is therefore,
Integrate( sqrt(9-x^2) from x=-3 to x=3)
scores on the sat verbal test in recent years follow approximately the n(515, 109) distribution. how high must a student score in order to place in the top 5% of all students taking the sat?
Answers
We need to determine the score a student must achieve to place in the top 5% of all students taking the SAT Verbal test with an N(\(515, 109\)) distribution, which came out to be \(695\) marks.
Identify the mean (μ) and standard deviation (σ) of the distribution: In this case, µ \(= 515\) and σ\(= 109\).
Determine the percentile rank: To place in the top \(5%\)% of students, we need to find the score corresponding to the \(95th\) percentile, as this represents the point where \(95\)% of students have a lower score.
Use a standard normal (Z) table or calculator to find the Z-score corresponding to the \(95th\) percentile: A Z-score represents the number of standard deviations a data point is from the mean.
For the \(95th\) percentile, the Z-score is approximate \(1.645\).
Apply the Z-score formula to find the required SAT score: \(X =\) µ \(+ Z*\) σ. In this case, \(X = 515 + (1.645 *109)\).Calculate the result: \(X = 515 + (1.645 *109)\)
\(=515 + 179.305 = 694.305\).
Round up to the nearest whole number: Since a student's SAT score must be a whole number, round up to \(695\). A student must score \(695\) or higher on the SAT Verbal test to place in the top \(5\)% of all students taking the test, given the N(\(515, 109\)) distribution.
Learn more about standard deviation:
https://brainly.com/question/29808998
#SPJ11
How could the distance formula and slope be used to classify triangles and quadrilaterals in the coordinate plane?
Answers
~ Use the distance formula to measure the lengths of the sides.
~ Use the slope to check whether sides are perpendicular and form right angles.
~ Use the slope to check whether the diagonals are perpendicular to each.
I hope this helps ^-^
Look at the shapes and decide wheater to use (1) sine law(2) cosine law, or (3) SOHCAHTOA

Answers
The triangle ABC, the angle x is 36°.
Given that,
In the picture, we have triangles ABC.
We have to find the angle x.
The sides of the triangle are AB=3cm and AC=5cm.
We have the angle B is 90°.
We use the sine law.
In trigonometry, there are six fundamental ratios that are used to establish a connection between a right triangle's side-to-angle ratio and its angle. If the angle created by the base and hypotenuse of a right-angled triangle is, then
Perpendicular/hypotenuse = sin θ
base/hypotenuse = cos θ
tan θ = Base/Perpendicular
The three additional functions' values, cot, sec, and cosec, are dependent on the values of tan, cos, and sin, as shown below.
cot θ= perpendicular/base
sec θ=hypotenuse/base
cosec θ=hypotenuse/perpendicular
So,
Sin x=opposite side/hypothesis
Sin x=3/5
Sin x= 0.6
x= sin⁻¹(0.6)
x=36.86°
Approximately, x=36°
Therefore, The angle x is 36°.
To learn more about angle visit: https://brainly.com/question/28451077
#SPJ9
The function below shows the cost for Mrs. Franklin to go to a buffet with c of her
grandchildren.
f(c) = 6.85 +2.95c
a. What is the y-intercept, and what does it mean?
b. What is the slope, and what does it mean?
c. If Mrs. Franklin paid 18.65 for the buffet, how many of her grandchildren did she take
to the buffet?
Answers
Answer:
a. y-intercept: 6.85
b. m = 2.95
c. 4 grandchildren
Step-by-step explanation:
The equation is y = mx + b
m = the slope
b = y-intercept
Our equation is f(c) = 6.85 +2.95c
a. The y-intercept is 6.85
b. m = 2.95
c. We put 18.65 in to solve
18.65 = 6.85 + 2.95c
11.8 = 2.95c
c = 4 grandchildren
So, Mrs. Franklin took 4 grandchildren to the buffet.
Find the equation of the plane tangent to the surfacer=3u2i+(5u−v2)j+3v2kr=3u2i+(5u−v2)j+3v2kat the point P that is (approximately) P(12,9,3).z(x,y)=z(x,y)=
Answers
The equation of the plane tangent to the surfacer=3u2i+(5u−v2)j+3v2kr=3u2i+(5u−v2)j+3v2kat the point P that is P(12,9,3).z(x,y)=z(x,y)= 90x + 1296y + 810z = 14218.
To find the equation of the plane tangent to the surface at point P(12, 9, 3), we first need to find the partial derivatives of the surface with respect to u and v:
∂r/∂u = 6ui + 5j
∂r/∂v = -2vj + 6vk
Next, we can evaluate these partial derivatives at the point P(12, 9, 3) to get:
∂r/∂u = 6(12)i + 5j = 72i + 5j
∂r/∂v = -2(9)j + 6(3)k = -18j + 18k
Using these partial derivatives, we can find the normal vector to the tangent plane at point P by taking their cross product:
n = (∂r/∂u) x (∂r/∂v) = (72i + 5j) x (-18j + 18k)
= -90i - 1296j - 90k
Since the tangent plane passes through point P, its equation can be written in the form:
-90(x - 12) - 1296(y - 9) - 90(z - 3) = 0
Simplifying this equation gives:
-90x + 12960 - 1296y - 810z + 1458 = 0
or
90x + 1296y + 810z = 14218
Therefore, the equation of the plane tangent to the surface at point P is 90x + 1296y + 810z = 14218.
Know more about tangent here:
https://brainly.com/question/4470346
#SPJ11
A company does research on their product and finds that 3/5 of people who try the product, use it again. If 400 people try the product, how many would we expect to use it again? 120 240 80 30
Answers
Answer:
240
Step-by-step explanation:
maybe
Answer:
240
Step-by-step explanation:
3/5 of the people try it use it again.
so, it you divid you would get 3/2000 which is wrong.
but, if you multiply you would get 240.
3/5 x 400 = 240
Can someone please help me???

Answers
Answer:
B.) 2 / 15
Step-by-step explanation:
: )
Determine whether series is : absolutely convergent , conditionally convergent , divergent
show work for understanding
n2-2 1. En=1n2+1 η=1 nn 100 2.2 =2 (Inn)
Answers
The given series Σ((n² - 2)/(n² + 1)) is divergent. To determine whether the series is absolutely convergent, conditionally convergent, or divergent, we need to analyze the given series: Σ((n² - 2)/(n² + 1))
Let's break it down and analyze each part separately.
Analyzing the numerator: (n² - 2).As n approaches infinity, the dominant term in the numerator is n². Thus, we can say that (n² - 2) behaves similarly to n² for large values of n.
Analyzing the denominator: (n² + 1)
As n approaches infinity, the dominant term in the denominator is also n². Therefore, (n² + 1) behaves similarly to n² for large values of n.
Now, let's consider the ratio of the terms:
En = ((n² - 2)/(n² + 1))
To determine the convergence or divergence of the series, we can analyze the limit of the ratio as n approaches infinity.
η = lim(n→∞) ((n² - 2)/(n² + 1))
We can simplify the ratio by dividing both the numerator and denominator by n²:
η = lim(n→∞) ((1 - 2/n²)/(1 + 1/n²))
As n approaches infinity, the terms involving 1/n² tend to zero. Therefore, we have:
η = lim(n→∞) ((1 - 0)/(1 + 0)) = 1
The ratio η is equal to 1, which means the ratio test is inconclusive. It does not provide enough information to determine the convergence or divergence of the series.
To determine whether the series is absolutely convergent, conditionally convergent, or divergent, we need to explore other convergence tests.
Since the ratio test is inconclusive, let's try using the integral test to determine the convergence or divergence.
Absolute Convergence:If the integral of the absolute value of the series converges, then the series is absolutely convergent.
Let's consider the integral of the absolute value of the series:
∫[1, ∞] |(n² - 2)/(n² + 1)| dn
Simplifying the absolute value, we have:
∫[1, ∞] ((n² - 2)/(n² + 1)) dn
We can calculate this integral to determine if it converges.
∫[1, ∞] ((n² - 2)/(n² + 1)) dn = ∞
The integral diverges since it results in infinity. Therefore, the series is not absolutely convergent.
2. Conditional Convergence:
To determine if the series is conditionally convergent, we need to investigate the convergence of the series without considering the absolute value.
Let's consider the series without taking the absolute value:
Σ((n² - 2)/(n² + 1))
To analyze the convergence of this series, we can try applying the limit comparison test.
Let's compare it to a known series, the harmonic series: Σ(1/n).
Taking the limit as n approaches infinity:
lim(n→∞) ((n² - 2)/(n² + 1)) / (1/n)
We simplify this limit:
lim(n→∞) ((n² - 2)/(n² + 1)) * (n/1)
This simplifies further:
lim(n→∞) ((n³ - 2n)/(n² + 1))
As n approaches infinity, the dominant term in the numerator is n³, and the dominant term in the denominator is n².
Therefore, the limit becomes:
lim(n→∞) (n³/n²) = lim(n→∞) n = ∞
The limit is divergent, as it approaches infinity. This implies that the given series also diverges.
In conclusion, the given series Σ((n² - 2)/(n² + 1)) is divergent.
To learn more about convergent or divergent visit:
brainly.com/question/31990142
#SPJ11
Solve the compound inequality and graph its solution:8r-3 ≥7r - 7 or 2r + 4≤ r-3
Answers
Answer:
Step-by-step explanation:
o solve the compound inequality, we'll start by solving each inequality separately, and then find the intersection of their solutions.
For the first inequality: 8r - 3 ≥ 7r - 7
Adding 7r to both sides: 8r - 3 + 7r ≥ 7r - 7 + 7r
Combining like terms: 15r - 3 ≥ 14r
Subtracting 14r from both sides: 15r - 14r - 3 ≥ 0
Combining like terms: r - 3 ≥ 0
Adding 3 to both sides: r ≥ 3
For the second inequality: 2r + 4 ≤ r - 3
Subtracting 2r from both sides: 2r + 4 - 2r ≤ r - 3 - 2r
Combining like terms: 4 ≤ -r - 3
Adding r and 3 to both sides: 4 + r + 3 ≤ -r
Combining like terms: 7 ≤ -r
Multiplying both sides by -1: r ≤ -7
The solution to the compound inequality is the intersection of the solutions to each inequality, which is the range of r that satisfies both conditions. So, the solution is 3 ≤ r ≤ -7.
To graph the solution, we can plot the two inequalities on the number line, and shade the region between 3 and -7:
I need help. This is a geometry project, and I need a reason why this picture is relevant to corresponding angles? It would also help if I could get a definition for corresponding angles. Please help me. I need this done today!

Answers
Corresponding angles: the angles which occupy the same relative position at each intersection where a straight line crosses two others. If the two lines are parallel, the corresponding angles are equal (from Dictionary)
It's basically a line crossed two parallel lines and the angles formed in the same place are called corresponding angles. Also they share the same angle only if the two lines are paralleled.
What steps are needed to plot another point on this graph of equivalent ratios?
.
On a coordinate plane, points (2, 1), (4, 2), (6, 3), and (12, 6) are plotted.
Start at any point on the graph. Move up 2 spaces and right 1 space, and then plot a point.
Start at any point on the graph. Move up 1 space and right 2 spaces, and then plot a point.
Start at any point on the graph. Move down 2 spaces and left 1 space, and then plot a point.
Start at any point on the graph. Move down 2 spaces and left 2 spaces, and then plot a point.
Answers
Answer:
Start at any point on the graph. Move up 1 space and right 2 spaces, and then plot a point.
Explanation:
Look at the coordinates (4, 2) and (6, 3) that I graphed on the chart. If you move 1 space up, and 2 spaces to the right, it leads to the coordinates (6, 3)

If the two spinners below are spun, what is the probability that the numbers will add to more than 4?
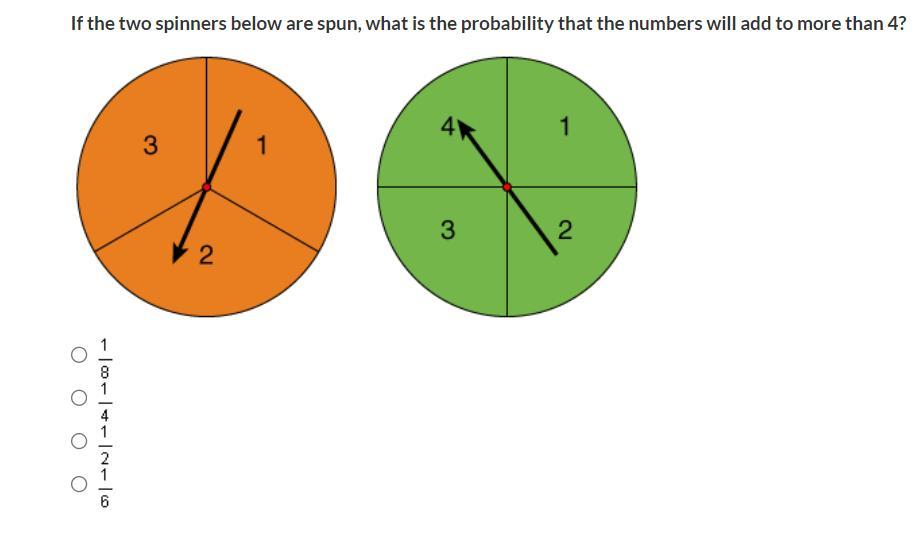
Answers
Answer: The answer is 1/4.
Step-by-step explanation:
The product of which expression contains four decimal places?
O 5.3478x6.4214
O 6.4x9.1
O 521x3.82
O 14.2x0.784
???
Answers
Answer:
45.2x0.784
Step-by-step explanation:
This problem equals 35.4368, which has four decimal points
Probability mathematic

Answers
Answer:
1/9
Step-by-step explanation:
Probability = Expected outcome/Total outcome
From the given pi chart,
Total outcome = 360degrees (since the total angle in a circle is 360 degrees)
Since we to find the probability of scoring a 5, we can see that the angle when he scores a 5 is 40degrees, hence;
Expected outcome = 40degrees
Pr(scoring a 5) = 40/360
Pr(scoring a 5) = 1/9
Hence the probability of scoring a 5 is 1/9
Answer:
1/9
Step-by-step explanation:
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty.
Divide the number of events by the number of possible outcomes.
What is the equation of the line whose y-Intercept is 3 and slope is 1?
Answers
y = x + 3
as x increases by 1, y increases by 1 (Slope)
when x equals 0, y equals 3 (y-intercept)
Triangle DEF contains right angle E. If angle D measures 55° and its opposite side measures 7.6 units, what is the measure of side
DF? Round your answer to the nearest hundredth.
A. 5.34 units
B. 6.38 units
C. 9.06 units
D. 9.28 units
Answers
Answer:
D. 9.28 units
Step-by-step explanation:
DF is the hypotenuse of the triangle.
\(\frac{sin(A)}{a} =\frac{sin(B)}{b}\)
\(\implies \frac{sin(55)}{7.6} =\frac{sin(90)}{DF}\)
\(\implies DFsin(55) =7.6sin(90)\)
\(\implies DF =\frac{7.6sin(90)}{sin(55)}\)
\(\implies DF =9.277886875...\)
\(\implies DF =9.28\ \textsf{units (nearest hundredth)}\)
La banqueta que rodea un jardín rectangular es de 4 metros de ancho. El jardín tiene
12 metros más de largo que de ancho. Si el área del jardín con la banqueta es de 1,728
m2, ¿cuáles son las dimensiones del jardín?
Tomar en cuenta que:
Ancho del jardín (sin banqueta): x
Answers
Answer:
jbhbchbhvbbhcbrhfbcbhshshbhsvhbhv;b;rvbhbhcrbihcbhc
Step-by-step explanation:
A study that uses both manipulated and measured variables in a factorial design is called a(n) _____ design.
a. mixed repeated measures and independent groups
b. IV X PV
c. 2x2
d. multiple correlation
Answers
A study that uses both manipulated and measured variables in a factorial design is called a(n) option b. IV X PV design.
In this design, there are two or more independent variables (IVs) that are manipulated by the researcher.
And one or more measured variables, also known as participant variables (PVs), that are measured but not manipulated.
Factorial designs are used to investigate the effects of multiple independent variables on a dependent variable.
As well as the interactions between the independent variables.
The IV X PV design is a specific type of factorial design.
That includes at least one measured variable in addition to the manipulated independent variables.
Option A is incorrect because mixed repeated measures and independent groups are types of designs .
That describe how participants are assigned to different groups in a study, whereas the IV X PV design describes the types of variables that are used in a study.
Option C describes a specific type of 2x2 factorial design, which includes two independent variables, each with two levels.
Option D describes a design that is used to investigate the relationship between multiple measured variables and a single dependent variable.
Learn more about variables here
brainly.com/question/13930388
#SPJ4