For a field trip 5 students rode in cars and
the rest filled ten buses. How many students
were in each bus if 215 students were on the
trip?
Answers
Answer:
21
Plz mark me brainliest
Step-by-step explanation:
Answer:21 students were on each bus.
Step-by-step explanation:
215-5=210
210/10=21 the number of students divided by the number of buses
Related Questions
Please help!!!!!!
Explain the answer

Answers
Answer:
I think they are.
Step-by-step explanation:
Because they are both 39 and 34 degrees so if x and y are the same number they are similar.
andy can run 20 miles in 6 hours. how much miles can he run in 1 hour.
Answers
I see that this is a rate of change time of problem
If andy can run 20 miles in 6 hours, than our goal is to find out how much he runs in a hour
So, we just have to divide 20 by 6.
It's sorta hard to explain
Questions?
Anyhow, the answer is around 3.3 miles per hour
Answer:
3.33 miles
Step-by-step explanation:
We Know
Andy can run 20 miles in 6 hours.
How many miles can he run in 1 hour?
We Take
20 / 6 ≈ 3.33 miles
So, Andy can run about 3.33 miles in 1 hour.
can someone please help

Answers
Answer:
x = 13
Step-by-step explanation:
→ Remember the amount of degrees a triangle sums to
180°
→ Make an equation
8x - 44 + 8x - 44 + 8x - 44 = 180
→ Simplify
24x - 132 = 180
→ Add 132 to both sides
24x = 312
→ Divide both sides by 24
x = 13
What’s the area in mmsquared?

Answers
Answer:
1384.74 mm²
Step-by-step explanation:
We Know
Area of circle = r² · π
diameter = 42 mm
radius = 42 / 2 = 21 mm
π = 3.14
We take
21² · 3.14 = 1384.74 mm²
So, the area of the circle is 1384.74 mm²
Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.
Steve is trying to determine the height of a flagpole using the flagpole's shadow. Early in the morning, the shadow of the flagpole is 30 feet long. Steve is 6 feet tall, and his shadow is 9 feet long at the same time.
The height of the flagpole is ___ feet.
Plz Answer ASAP! Thank you!
Answers
Answer:
20
Step-by-step explanation:
Since Steve is 6 feet tall and his shadow is 9 feet long we can do 9÷6=1.5 then 30÷1.5=20 so 20 is the answer (also I got it right on the test)
The height of the flagpole is 20 feet.
What is the ratio of two quantities?Suppose that we've got two quantities with measurements as 'a' and 'b'
Then, their ratio(ratio of a to b) a:b
Given;
The Length of flagpole shadow = 30 ft
The Steve height = 6 ft
The Length of Steve height shadow = 9 ft
The height and shadow length of the two follows the same ratio, just like similar triangles;
The height of flagpole/flagpole shadow length = height of Steve / Steve shadow height
Substituting the values;
h/30 = 6/9
h = 6/9 × 30 = 20 ft
Thus, the Flagpole height is 20 ft.
Learn more about ratio here:
brainly.com/question/186659
#SPJ2
The volume of a cube is 8mm3.
What is the length of its side?
Answers
Answer:
the length of cube
is 2 mm
Answer:
2m
Step-by-step explanation:
A cube is a 3-dimensional object with all sides of equal length. So, length = breadth = height
Let the side of cube be x.
Then Volume of cube = x * x * x
So, length (side) of cube is 2m
What is the solution to the equation
x = –6
x = –1
x = 1
x = 2

Answers
When we're solving equations, our prime goal is to isolate the variable. We can do this by using inverse operations to combine like terms.
Examples:
The inverse operation of addition is subtraction, and vice versa.The inverse operation of an exponent is taking the root of the exponent, and vice versa.Solving the Question\(\sqrt[3]{5x-4}=\sqrt[3]{7x+8}\)
⇒ Here, both sides are being taken to the square root of 3. To remove this, we can raise both sides to the power of 3:
\((\sqrt[3]{5x-4})^3=(\sqrt[3]{7x+8})^3\\5x-4=7x+8\)
⇒ Let's move our x variable to the right side of the equal sign and the numbers to the left side. Start by subtracting 5x from both sides:
\((\sqrt[3]{5x-4})^3-5x=(\sqrt[3]{7x+8})^3\\5x-4=7x+8-5x\\-4=2x+8\)
⇒ Now, subtract 8 from both sides:
\(-4-8=2x+8-8\\-12=2x\)
⇒ Finally, divide both sides by 2 to isolate x:
\(\dfrac{-12}{2}=\dfrac{2x}{2}\\\\-6=x\)
Answerx = -6
Answer:
A
Step-by-step explanation:
EDGE 2019
Which of the following answers is correct?

Answers
The function d/dx (f/g) = 2 gives the value of c as -4.
What is Quotient Rule?The denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator, is how the Quotient Rule defines the derivative of a quotient.
Given:
f(x) = 1/2x and g(x) = 1/ (3x + c)
Using Quotient rule
d/ dx (f/g)
= g f' - f g- / g²
So, d/dx ( 3x+c / 2x )
= [3x -1(3x+c)] / 2x²
= -c/ 2x²
Now out x= 1
Also, d/dx (f/g)= 2
-c/ 2 = 2
c= -4.
Learn more about Quotient Rule here:
https://brainly.com/question/29255160
#SPJ1
The length of a rectangular sign is 5 times its width. if the signs perimeter is 36 inches,what is the signs area?
Answers
Answer:
length is 15
width is 3
Step-by-step explanation:
3 * 5 is 15
3+3+15+15= 36
The perimeter of a square is 80 minus 64 y units. Which expression can be used to show the side length of one side of the square?
Answers
The perimeter of a square is 80 minus 64 y units. Which expression can be used to show the side length of one side of the square?
Answer · 1 vote
Perimeter of the square80-64yA square has 4 sides, so divide the perimeter by 4:(80-64y) / 480 divided by 4 is 2064y divided by 4 is 16yOne side of the ..
Answer:
Its C
Step-by-step explanation:
took the test
A ball is dropped freely from a height of 150 m. Calculate a) How much has it descended after 4 seconds?, b) What speed does it lack to reach the ground?
Answers
This problem implies more cases to solve as well as the use of other formulas that we can use in the subject of free fall, if we read our exercise again, we will realize that we only have a height of 150 meters from where it is dropped freely a ball. To proceed to resolve, we collect the data.
Distance descended at 4 secondsWhat speed does it have at 4 seconds?How far does it take to reach the ground?Data:
h = 150 m
g = 9.8 m/s²
a) Obtain the distance at 4 seconds when the ball descendsIn order to obtain the distance traveled in 4 seconds, we can use the following formula:
\(\bf{\displaystyle h={{v}_{0}}t+\frac{g{{t}^{2}}}{2} }\)
Remember, that as it is a free fall, the initial speed is null, that is, zero. So the formula reduces:
\(\bf{\displaystyle h=\frac{g{{t}^{2}}}{2} }\)
We are going to place the 4 seconds in the “t” of time. Thus:
\(\bf{\displaystyle h=\frac{g{{t}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right){{\left( 4s \right)}^{2}}}{2} }\)
Carrying out the indicated operations:
\(\bf{\displaystyle h=\frac{g{{t}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right)16{{s}^{2}}}{2}=\frac{156.8m}{2}=78.4m }\)
That is to say that the height at 4 seconds is 78.4 meters.
b) What speed will it have after 4 seconds?
For the velocity at 4 seconds, we use the following formula:
\(\bf{\displaystyle {{v}_{f}}={{v}_{0}}+gt}\)
Remember, that since there is no initial speed because it is free fall, then the formula is reduced:
\(\bf{\displaystyle {{V}_{f}}=gt }\)
Substituting our data and calculating:
\(\bf{\displaystyle {{v}_{f}}=gt=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 4s \right)=39.2\frac{m}{s} }\)
So the speed at 4 seconds is 39.2 m/s.
c) Distance it takes to reach the ground.
Although it seems difficult to solve this section, it is not. It's very easy, let's remember that after 4 seconds it has traveled 78.4 meters and that the height from where the ball was dropped is 150 meters, so the difference is the amount that remains to reach the ground, that is:
\(\bf{\displaystyle {{h}_{T}}={{h}_{1}}+{{h}_{2}}}\)
It is as if we had:
\(\bf{\displaystyle 150=78.4+{{h}_{2}} }\)
Clearing "h2" what would be the distance to reach the ground.
\(\bf{\displaystyle {{h}_{2}}=150-78.4=71.6m }\)
In other words, we need to travel 71.6 meters to reach the ground.
(Build your own model for this problem.) Kate’s Cakes is a boutique cake shop in AJ’s Fine Foods supermarket. Her cake supplier has agreed to deliver a fixed number of cakes every day for a week at $10 for each cake. At the end of the week, Kate may change her order for the following week. Kate has kept close track of daily cake demand. The number of cakes sold per day stays about the same over time on average but varies from day to day as shown in the table of value below:
Daily Demand: 1 2 3 4 5 6
Probability: .1 .2 .25 .25 .15 .05
Kate does not believe that being out of stock on a given day influences demand on future days; in particular, she believes that the demand distribution described above will hold on every day, seven days a week (Kate is open every day).
Kate’s initial inventory of cakes is zero. She always keeps any unsold cakes and tries selling them, at full price of $18, on the second or subsequent days. Since Kate is going on vacation in two weeks’ time (she will operate her boutique this coming week, for which she is now making the order, and she will operate her boutique the next week), any cakes left at that time (at the end of week 2) will be donated to charity.
Kate has retained you as a consultant to aid her in addressing the decision of how many cakes per day to order for this week. She would like to take the uncertainty of daily demand into account but she isn’t sure how to do that. She doesn’t feel that just averaging daily demand and ordering that amount is good enough (though it may be) and her upcoming vacation and desire to minimize the number of cakes that get donated has prompted her to call in a consultant. How many cakes per day should Kate order for this week?
Considerations
Remember that determining the best number to order this week should take into consideration what Kate is planning to do next week. Or vice versa.
a. How many cakes per day should Kate order for this week?
b. Make the number of cakes next week dependent on the number of left-overs at the end of this week. Does that change your estimate of how many should be ordered this week?
c. Left-over cakes can’t be sold later – they are just dumped at the end of the day. Does this change the number you want to order for this week?
d. Day-old cakes sell for $12 and two-day-old cakes are donated.
Answers
To determine how many cakes per day Kate should order for this week, we can calculate the expected profit for each possible daily order quantity and choose the one that maximizes profit.
(a) Here are the steps:
1. Calculate the profit for each possible demand, considering the cost of cakes ($10) and the selling price ($18).
2. Multiply the profit by the probability of each demand level.
3. Sum up the expected profits for all demand levels. Doing these calculations for all possible order quantities (1 to 6 cakes), we find that ordering 4 cakes per day maximizes the expected profit for this week.
(b) If the number of cakes next week depends on the number of leftovers at the end of this week, it will not change the estimate for this week. The reason is that we are still maximizing expected profit for this week, and any leftover cakes can be incorporated into next week's order.
(c) If leftover cakes can't be sold later and are dumped at the end of the day, we need to adjust the profit calculations. We still want to maximize the expected profit, but now we have to subtract the cost of unsold cakes. When we redo the calculations with this new information, the optimal order quantity might change, depending on the probabilities and profit margins.
(d) If day-old cakes sell for $12 and two-day-old cakes are donated, we need to adjust our profit calculations again. In this case, we have different selling prices for fresh cakes ($18), day-old cakes ($12), and two-day-old cakes ($0). Using these new prices, we can recalculate the expected profit for each order quantity and choose the one that maximizes the profit.
Learn more about profit here, https://brainly.com/question/19104371
#SPJ11
a. Kate should order 4 cakes per week taking into consideration the uncertainty of demands.
b. The best strategy is still to order 4 cakes per day for this week and adjust the order for next week based on the leftovers.
c. Kate should order 3 cakes per day for this week to minimize waste.
d. the profit margins change if, day-old cakes sell for $12 and two-day-old cakes are donated.
a. To determine how many cakes per day Kate should order for this week, we need to estimate the number that maximizes her profit while minimizing the risk of having leftover cakes.
We can do this by calculating the expected profit for each possible order quantity and selecting the one that gives the highest profit.
We can calculate the number of cakes by following the steps
1. Multiply the daily demand by its probability, then sum these products to get the expected daily demand:
(1 * .1) + (2 * .2) + (3 * .25) + (4 * .25) + (5 * .15) + (6 * .05) = 3.4 cakes
2. Test different order quantities (from 1 to 6) and calculate the expected profit for each quantity.
3. Select the order quantity with the highest expected profit.
For this problem, Kate should order 4 cakes per day for this week.
b. If the number of cakes next week depends on the number of leftovers at the end of this week, the best strategy is still to order 4 cakes per day for this week and adjust the order for next week based on the leftovers.
c. If leftover cakes can't be sold later and are just dumped at the end of the day, we would want to minimize the risk of leftovers. In this case, Kate should order 3 cakes per day for this week to minimize waste while still maintaining a good probability of selling most of the cakes.
d. If day-old cakes sell for $12 and two-day-old cakes are donated, the profit margins change, and the expected profit calculation should be updated accordingly.
After recalculating, Kate should still order 4 cakes per day for this week, as the order quantity provides the highest expected profit with this new pricing structure.
Learn more about expected profit calculation : https://brainly.com/question/28851824
#SPJ11
you have 3 bottles of lotion each bottle contains 3.78 mL 4.52 mL and 2.72 mL of lotion how much lotion do you have in total.
Answers
Answer:
11.02
Step-by-step explanation:
use a calculator? add the 3 numbers up
Find the slope between the points (1,3) and (9,27)
Answers
Answer:
slope = 3
Step-by-step explanation:
calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (1, 3 ) and (x₂, y₂ ) = (9, 27 )
m = \(\frac{27-3}{9-1}\) = \(\frac{24}{8}\) = 3
\(\mathbb{FINAL\:ANSWER:}\)
\(\huge\boxed{\sf\:Slope=3}}\)
\(\mathbb{SOLUTION\:WITH\:STEPS:}\)
Hi! Hope you are having a nice day!
We are given 2 points that the line passes through, so we can use the slope formula and find the slope.
Slope Formula:
\(\displaystyle\frac{y2-y1}{x2-x1}\)
\(\displaystyle\frac{27-3}{9-1}\)
\(\displaystyle\frac{24}{8}\)
The fraction can be reduced:
\(\displaystyle\frac{3}{1}\)
which is the same as
\(3\)
Hope you could understand everything.
#CarryOnLearning
HURRY!! A church group set off from their church at 9:00AM for the beach. The group had to change a tire at 9:31AM. The group noted that the trip took them 63 minutes to finish. What time did the church group arrive at the beach?
Answers
answer:
10:03 am
explanation:
9:00 am + 1 hour (60 min) + 3 min = 10:03 am.
Consider this system of equations.
p=2n
p-5 = 1. 5n
What value of n makes the system of equations true?
Enter your answer in the box.
Answers
Therefore, the value of n that makes the system of equations true is n = 10.
Given:
p = 2n
p - 5 = 1.5n
Substituting the value of p from the first equation into the second equation, we have:
2n - 5 = 1.5n
Next, we can solve for n by subtracting 1.5n from both sides of the equation:
2n - 1.5n - 5 = 0.5n - 5
Simplifying further:
0.5n - 5 = 0
Adding 5 to both sides of the equation:
0.5n = 5
Dividing both sides by 0.5:
n = 10
Therefore, the value of n that makes the system of equations true is n = 10.
Learn more about equations here
https://brainly.com/question/29657992
#SPJ11
Please help and explain.

Answers
Answer:
R = 13 cm, x = 5 cm
Step-by-step explanation:
We can see, that AO = BO = EO
First, we have to find AO from ∆OAD by using the Pythagorean theorem:
\( {ao}^{2} = {ad}^{2} + {x}^{2} \)
\( {ao}^{2} = 144 + {x}^{2} \)
\(ao > 0\)
\(ao = \sqrt{144 + {x}^{2} } \)
Now, let's write that EO = (8 + x)
Since AO = EO, we can write an equation:
\( \sqrt{144 + {x}^{2} } = 8 + x\)
Let's square the whole equation:
\(144 + {x}^{2} = ( {8 + x})^{2} \)
\(144 + {x}^{2} = 64 + 16x + {x}^{2} \)
\( {x}^{2} - {x}^{2} - 16x = 64 - 144\)
\( - 16x = - 80\)
Let's divide both sides of the equation from -16:
\(x = 5\)
OB = 8 + x = 8 + 5 = 13 (radius)
ms. wood has a collection of 25 questions. how many different tests of 5 questions each can be made from the set of questions?
Answers
There are 25,053,600 different tests of 5 questions each that can be made from Ms. Wood's collection of 25 questions.
To find the number of different tests of 5 questions each that can be made from a set of 25 questions, you can use the combination formula. The combination formula is:
n! / (r! * (n-r)!)
Where n is the total number of items and r is the number of items being chosen at a time.
In this case, n is 25 (the total number of questions) and r is 5 (the number of questions per test). Plugging these values into the formula gives:
25! / (5! * (25-5)!) = 25! / (5! * 20!) = 25 * 24 * 23 * 22 * 21 / (5 * 4 * 3 * 2 * 1) = 25,!053,!600
To know more about combination formula visit :
brainly.com/question/14685054
#SPJ4
Help please what is the slope of this

Answers
Answer:
1/2
Step-by-step explanation:
Rise over run. The rise is 4 the run is 8. Simplify.
which measure of variability is the most direct way to measure how dispersed a set of scores is?
Answers
The most direct way to measure how dispersed a set of scores is, is by using the range. The range is calculated by subtracting the lowest score from the highest score in the dataset, which gives a quick and easy measure of the spread of the scores.
However, the range can be influenced by extreme scores and may not provide a complete picture of the variability. Other measures of variability, such as the standard deviation and variance, take into account the variability of all scores in the dataset and provide a more robust measure of variability.
To know more about range and standard deviation, visit:
https://brainly.com/question/30713935
#SPJ11
Given that P(x) = ax^2 + bx + 1. P(1) 6
and P(-1) = 2, determine the values of a
and b
Please I Ned help ASAP
Answers
Answer:
a=3
b=2
Step-by-step explanation:
P(x) = ax^2 + bx + 1
P(1)= 6
6= a(1)^2 + b(1) +1
6 = a +b+1
6-1 = a+b
5 = a+b
P(-1) = 2
2 = a( -1)^2 + b(-1) +1
2 = a(1) -b +1
2-1 = a-b
1 = a+b
We have 2 equations and 2 unknowns
Add the two equations together
5 = a+b
1 = a-b
----------------
6 = 2a
Divide by 2
6/2 = 2a/2
3 =a
Now find b
5 =a+b
5 =3+b
Subtract 3 from each side
5-3 =3+b-3
2=b
.Independent random samples of business managers and college economics faculty were asked to respond on a scale from 1 (strongly disagree) to 7 (strongly agree) to this statement: Grades in advanced economics are good indicators of students’ analytical skills. For a sample of 70 business managers, the mean response was 4.4 and the sample standard deviation was 1.3. For a sample of 106 economics faculty, the mean response was 5.3 and the sample standard deviation was 1.4.
a) Test, at the 5% level, the null hypothesis that the population mean response for business managers would be at most 4.0. (10marks)
b) Test, at the 5% level, the null hypothesis that the population means are equal against the alternative that the population mean response is higher for economics faculty than for business managers. Assume unequal variance.
Answers
Step-by-step explanation:
a) The test statistic is (4.4-4)/(1.3/sqrt(70)) = 2.83. The p-value is 0.0023. Since the p-value is less than 0.05, we reject the null hypothesis.
b) The test statistic is (5.3-4.4)/sqrt((1.4^2/106)+(1.3^2/70)) = 4.09. The p-value is less than 0.0001. Since the p-value is less than 0.05, we reject the null hypothesis.
1. Which of the following measures would NOT produce a triangle? Choose all that apply.
three sides: 3 cm, 5 cm, and 7 cm
three sides: 5 cm, 7 cm, and 9 cm
three sides: 5 cm, 9 cm, and 15 cm
three sides: 3 cm, 5 cm, and 10 cm
Answers
Answer:
I believe the answers are :
5 cm, 9cm, and 15 cm
3 cm, 5 cm, and 10 cm
Step-by-step explanation:
When 2 sides that are not the hypotenuse are added and are less than the hypotentuse, a triangle cannot be formed.
The value of -4^2 is _____.
8
-16
16
-8
And please tell me why
Answers
Answer:
16
Step-by-step explanation:
A negative times a negative is a positive. -4^2 is equal to -4 times -4. This would give us 16.
What is equivalent to 36^-1/2

Answers
74/360 in simplest form
Answers
Answer:
37/180
Step-by-step explanation:
Reduce this fraction by dividing both sides by 2. We get 37/180, which cannot be reduced further; 37 and 180 have no common factor.
Determine whether the integral is convergent or divergent. ∫59/root(1-x^2) dx convergent or divergent If it is convergent, evaluate it. (If the quantity diverges, enter DIVERGES.)
Answers
The integral \(∫59/sqrt(1-x^2)\) dx is convergent, and its value is \(59π/a^2\). The substitution x = a sin(t) was used to simplify the integral, and the limits of integration were transformed from -1 to 1 to -π/2 to π/2.
The integral\(∫59/sqrt(1-x^2)\) dx is a definite integral that represents the area under the curve of the function\(59/sqrt(1-x^2)\) between its limits of integration. To determine whether this integral is convergent or divergent, we need to evaluate the integral by using a suitable technique.
We can begin by noting that the integrand is of the form \(f(x) = k/√(a^2-x^2)\), where k and a are constants. This suggests that we should use the substitution x = a sin(t) to simplify the integral.
Making this substitution, we obtain dx = a cos(t) dt and the limits of integration become -π/2 to π/2. The integral now becomes:
\(∫59/sqrt(1-x^2) dx = ∫59/(a cos(t)) a cos(t) dt\)\(= 59∫(1/a^2) dt = 59t/a^2\)
Evaluating the integral from -π/2 to π/2, we obtain:
\(∫59/sqrt(1-x^2) dx\)\(= 59(π/2 - (-π/2))/a^2\)\(= 59π/a^2\)
Since the limits of integration are finite, and the integral has a finite value, we can conclude that the integral is convergent. Evaluating the integral using the substitution x = a sin(t), we obtain the value\(59π/a^2\).
Learn more about convergent here:
https://brainly.com/question/31064900
#SPJ4
Select the equation that could represent the relationship between f(x) and g(x).
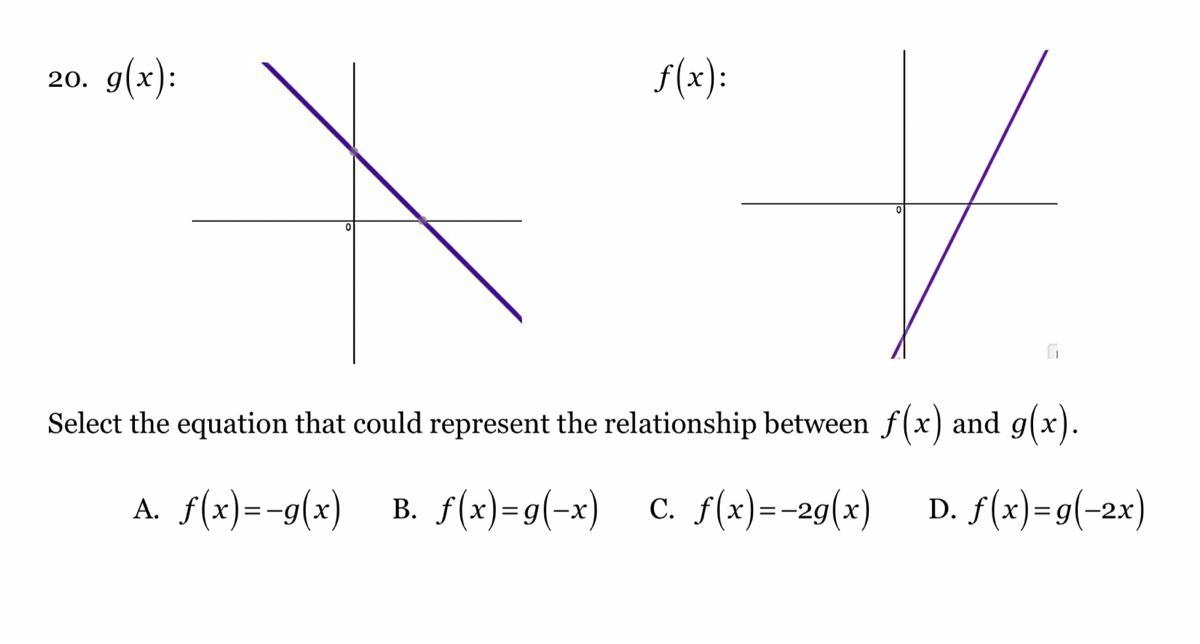
Answers
Answer:
C
Step-by-step explanation:
First, f(x) and g(x) are mirror image over the x-axis. so add a -ve in front.
Second, f(x) is about 2x steeper than g(x), that is its slope is doubled. so add a 2 in front.
Thus, f(x) = -2 g(x)
Kristin and her family left their campsite to take a bike ride. They biked 5 miles west and then 12 miles north. How far are they from their campsite? Round to the nearest 10th if necessary.
Answers
Answer:
they are 17 miles away from their campsite.
Step-by-step explanation:
we get the answer by adding the miles traveled north to the miles traveled west, and we get the total number of miles they traveled away from their campsite.
5 + 12 = 17
The length of one of the parallel sides of a trapezium is 5 more than the other parallel side. The perpendicular height is 7 cm. Write an expression for the area
Answers
Answer:
7x+35/2
Step-by-step explanation:
The area of a trapezoid is \(\frac{(b_1+b_2)}{2}\cdot h\), where b1 and b2 are the two bases and h is the height. Because b2 is 5 more than b1, which we will represent as x, we have the two bases as x and x + 5 respectively. Plugging into the equation, we have \(\frac{2x+5}{2}\cdot 7\) .We have this as (x+5/2)(7), which is 7x+35/2