Five divided by the sum of a and b?
Answers
Answer:
The sum of a and b is a+b.
Step-by-step explanation:
5 divided by the sum of a and b is 5/ (a+b).
The final answer is 5/ (a+b)~
Answer:
The sum of a and b is a+b.
Step-by-step explanation:
5 divided by the sum of a and b is 5/ (a+b).
The final answer is 5/ (a+b)
hope that helps:)
Related Questions
can somebody help with this.?

Answers
How would you describe the shape of the normal distribution?
Answers
The shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).
What is a normal distribution?
A normal distribution is a function on some random variables, which represent the set of all those random variables in a symmetrical bell shape about the mean value.
It shows that the probability of occurrence of some data which is distributed over a function is more at or around the mean.
It is also known as probability distribution curve.
The normal distribution has two parameters:
MeanStandard deviationWhat is the shape of the normal distribution?
The normal distribution curve is at it's peak at the mean value. This shows that the probability of occurrence of the data or value is more concentrated or distributed about the mean. It is also symmetric about the mean. As we more further from the mean, we see that the normal distribution curve gradually decreases showing that the probability of occurrence of the data or the values decreases. The shape that this curve forms is like a bell-shaped. So the shape of normal distribution is bell shape.
Hence, the shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).
Know more about "normal distribution" here: https://brainly.com/question/15103234
#SPJ4

B. What fraction of the letters of the English language are vowels? (points)
Answers
Answer:
5/26.
If you count y as a vowel it is 3/13
Step-by-step explanation:
I WILL GIVE BRANLISET

Answers
Answer:
y axis: (0, 12)
x axis: (18, 0)
Quadrant I: (4.5, 10.6)
Quadrant II: (-15, 21)
Quadrant III: (-3/4, -4 1/9)
Quadrant IV: (3, -7)
Step-by-step explanation:
Integers used for each Quadrant.
Quadrant one: x axis = positive, y axis = positive
Quadrant two: x axis = negative, y axis = positive
Quadrant three: x axis = negative, y axis = negative
Quadrant four: x axis = positive, y axis = negative
(0,12) = goes to the y axis
(3,-7) = goes to quadrant 4
(-15,21) = goes to quadrant 2
(18,0) = goes to the x axis
(4.5,10.6) = goes to quadrant 1
(-3/4, -4 1/9) = goes to quadrant 3
Write the equation for a line in slope intercept form that is parallel to the line 2x + 3y = 6 and passes through the point (0, 4).
Answers
Answer:
Let us find the slope of the line : x+ 4y = 6
we can write it as 4y = -x +6
y = -(1/4) x + ( 6/4)
slope of the line y= mx + b is m
so here slope = m = -1/4
because we have to find a paraller line so the slope for required line would be same : -1/4
equation of the line having slope m and passing through x1 y1 is :
Y= m( X-x1) + y1
let's plug m= -1/4 x1= -8 and y1 = 5
Y= (-1/4) ( X- -8) + 5
Y= ( -1/4) ( x+8) + 5
Y= (-1/4)( X ) + (-1/4)( 8) + 5
Y= (-1/4) x + 3
Let us now work on second part :
given line is : 2x- 3y = 12
let's write it -3y = -2x +12
y= (-2/-3) x + ( 12/ -3)
Y= ( 2/3) x - 4
slope of this line is 2/3
the required line is perpendicular to it
so the slope of required line = negative resiprocal of this slope =
(-1/ slope of this line ) = -1/( 2/3) = -3/2
Equation of line with slope m= -3/2 and passing through x1= 2 and y1 = 6 is :
Y= m( X-x1) + y1
Y= ( -3/2) ( X- 2) + 6
Y= (-3/2) X - 2(-3/2) + 6
Y= ( -3/2 ) X + 9
Answer : for part 1 : Y= ( 2/3) x - 4
Answer for part 2 : Y= ( -3/2 ) X + 9
Step-by-step explanation:
Write the ratio of 24 cats to 16 dogs in simplest form in 3 ways explain or show your work
Answers
Answer:
3:2
3 to 2
3/2
Step-by-step explanation:
24/16 reduces to 3/2.
Answer:
3/2 5/3 12/8
Step-by-step explanation:
how to solve this story problem. Newton buys 4 gallons of gasoline. He pays $8.64. How much does 1 gallon of gasoline cost
Answers
Answer:
$2.16 / gallon
Step-by-step explanation:
4 gallons were bought for $8.64
4 gallons = $8.64
1 gallon = ?
cross multiply and divide
$8.64 / 4 gallons = $2.16 per gallon
check:
$2.16 * 4 = $8.64
You divide $8.64 by 4
what is a axe on a graph?
Answers
Answer:
Plural of Axis. Pronounced "ak-seez". Axes often means the "x" and "y" lines that cross at right angles to make a graph. See: Axis (graph) Cartesian Coordinates.
Step-by-step explanation:
9t + 5(t + 3) = -(t + 13) + t
Answers
If we solve the given equation for t we get that t=-2
The equation given,
9t+5(t+3) = -(t+13) +t
⇒9t + 5t + 15 = -t -13 +t
⇒14t + 15 = -13 (∵-t+t=0)
⇒14t = -13-15 (bringing 15 from left hand side to right hand side the sign is flipped and 15 becomes -15)
⇒14t = -28
⇒\(t=\frac{-28}{14}\) (dividing both sides by 14)
⇒t = -2
Thus on solving the equation we get t = -2
Your question was incomplete but most probably your full question was
Solve for t when this equation is given, 9t+5(t+3) = -(t+13) +t
another problem on solving equation:
brainly.com/question/4092451
#SPJ4
In the Diagram, DEC is a ____ of ABC across line k.
rotation
glide reflection
reflection
translation
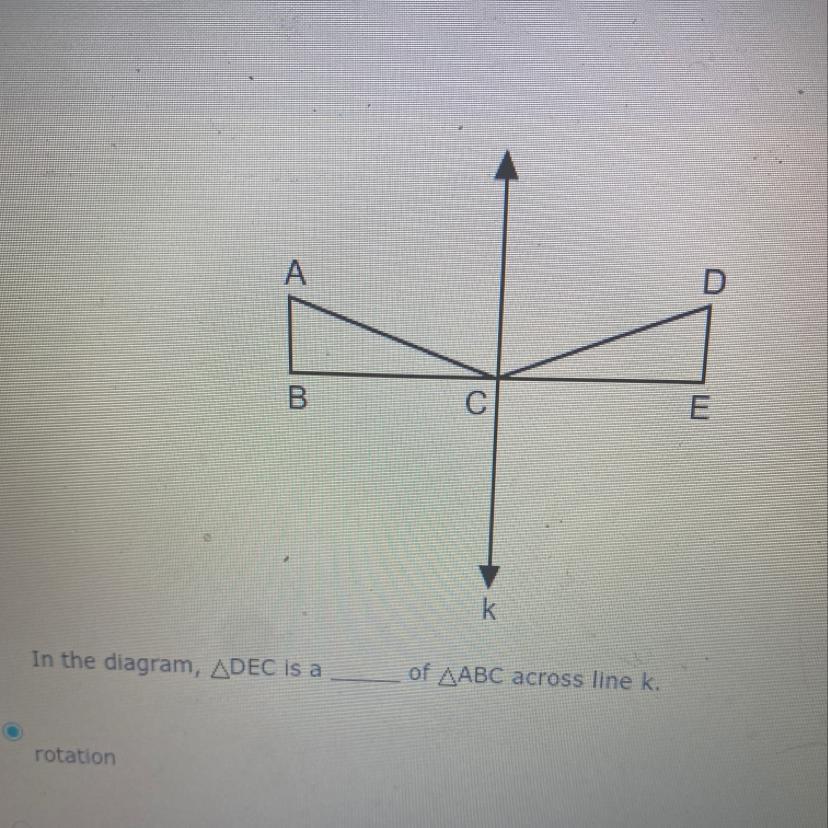
Answers
Answer:
Reflection
Step-by-step explanation:
A reflection is a mirrored image of a shape. Notice how DEC seems to be a "flipped" version of ABC, hence a mirrored image.
Cheers.
PLEASE HELP Which of the following types of data are likely to be normally distributed? Select all that apply

Answers
Answer: the correct answer is D and E
Step-by-step explanation:
The formula , where P = F/A pressure, F = force, and A = area, is used to calculate pressure. Solve this formula for F.
Answers
Answer:
Step-by-step explanation:
Just took the test
F=PA
Answer: F=P/A
Step-by-step explanation:
Two types of electromechanical carburetors are being assembled and tested. Each of the first type requires 11 minutes of assembly time and 2 minutes of testing time. Each of the second type requires 15 minutes of assembly time and 9 minutes of testing time. If 372 minutes of assembly time and 169 minutes of testing time are available, how many of the second type can be assembled and tested if all the time is used?
Answers
If all the available assembly and testing time is used, we can assemble and test 10 of the second-type carburetors.
Let's let x be the number of the first type carburetors and y be the number of the second type carburetors.
To minimize calculation, let's focus on just one of the constraints, say the assembly time constraint. We can write: \(11x + 15y ≤ 372\)
Dividing everything by 3: (note: dividing by 3 preserves the inequality
\()4x + 5y ≤ 124\)
Rewriting this as:
\(y ≤ (-4/5)x + 24.8\)
Notice that this is the equation of a line with slope -4/5 and y-intercept 24.8.
The graph looks like this: Graph of\(y ≤ (-4/5)x + 24\).
We can see from the graph that y ≤ (-4/5)x + 24.8 is satisfied for any point under the line.
For example, \((x,y) = (20, 4)\)satisfies the inequality, but \((x,y) = (20,5)\) does not.
Now we turn our attention to the testing time constraint:2x + 9y ≤ 169
Dividing everything by 1: (note: dividing by 1 preserves the inequality)2x + 9y ≤ 169Rewriting this as
\(y ≤ (-2/9)x + 18.8\)
Notice that this is the equation of a line with slope -2/9 and y-intercept 18.8.
The graph looks like this:
Graph of \(y ≤ (-2/9)x + 18\).8
We can see from the graph that \(y ≤ (-2/9)x + 18.8\) is satisfied for any point under the line.
For example,\((x,y) = (20, 2)\) satisfies the inequality, but\((x,y) = (20,3)\)does not.
Now we need to find the point on both lines that maximizes the number of second-type carburetors y.
This point will lie on the intersection of the two lines:\(y = (-4/5)x + 24.8y = (-2/9)x + 18\).
Solving this system of equations, we get:x = 112/11 and y = 4/11Rounded down to the nearest integer, we get:x = 10 and y = 0
Therefore, if all the available assembly and testing time is used, we can assemble and test 10 of the second-type carburetors.
Know more about equations here:
https://brainly.com/question/17145398
#SPJ11
An account earns simple interest. (a) Find the interest earned. (b) Find the balance of the account: $500 at 12% for 6 months
Answers
keeping in mind that a year has 12 months, so 6 months is really 6/12 of a year, and we can squeeze that to 0.5 year.
\(~~~~~~ \textit{Simple Interest Earned} \\\\ I = Prt\qquad \begin{cases} I=\textit{interest earned}\\ P=\textit{original amount deposited}\dotfill & \$500\\ r=rate\to 12\%\to \frac{12}{100}\dotfill &0.12\\ t=years\to \frac{6}{12}\dotfill &0.5 \end{cases} \\\\\\ I = (500)(0.12)(0.5) \implies I = 30\hspace{5em}\underset{\textit{accumulated amount}}{\stackrel{500~~ + ~~30}{\text{\LARGE 530}}}\)
1 3/4 cups of flour for one batch but he wants to make 1 1/2 batches. How many more cups of flour will he need
Answers
Answer:
\(2\frac{5}{8} cups = 1\frac{1}{2}\ batches\)
Step-by-step explanation:
Given
\(1\frac{3}{4} cups = 1\ batch\)
Required
Number of cups for \(1\frac{1}{2}\) batches
\(1\frac{3}{4} cups = 1\ batch\)
Multiply both sides by \(1\frac{1}{2}\)
\(1\frac{1}{2} * 1\frac{3}{4} cups = 1\ batch * 1\frac{1}{2}\)
\(1\frac{1}{2} * 1\frac{3}{4} cups = 1\frac{1}{2}\ batches\)
Express fractions as improper fractions
\(\frac{3}{2} * \frac{7}{4} cups = 1\frac{1}{2}\ batches\)
\(\frac{21}{8} cups = 1\frac{1}{2}\ batches\)
Express fraction as improper fraction
\(2\frac{5}{8} cups = 1\frac{1}{2}\ batches\)
Nadia charges $5.50 an hour for babysitting. She babysits 19.50 hours the first week of the month and 19 hours the second week of the month. Suppose Nadia raises her rate by $0.55 an hour. How many hours would she need to work to earn the same amount of money she made in the first two weeks of the month? Complete the explanation and give your answer. Nadia's new hourly rate is $ . She would need to work hours in the next two weeks to make the same amount she made in the first two weeks.
Answers
Answer:
Step-by-step explanation:
ind her earnings for the first two weeks of the month at the $5.50 an hour rate.
5.50 × (18 + 20.50) = 5.50 × 38.5
= 211.75
She earned $211.75 the first two weeks of the month.
Find her new hourly rate, if she raises her rate by $0.55.
5.50 + 0.55 = 6.05
Her new hourly rate is $6.05.
Find how many hours she would need to work at $6.05 an hour in order to earn $211.75.
211.75 ÷ 6.05 = 35
She would need to work 35 hours.
Answer fast please
8.
What is the 9th term in the quadratic sequence
shown below?
2, 5, 10, 17, 26, ...
A. 97
B. 82
C. 71
D. 65

Answers
Can someone help me?

Answers
Answer:
What are you trying to do you have not Explained to us
Step-by-step explanation:
Need help ASAP. How much water can this container hold? Use 3.14 to approximate pi, round your answer to the nearest hundredth

Answers
Answer:
2,134.57 or the bottom one
Step-by-step explanation:
I found the volume
Answer:
its D i did the Iready
Step-by-step explanation:
Solve the equation 5(x+6)+11=25−3x
Answers
Answer:
x=-2
Step-by-step explanation:
Let's solve your equation step-by-step.
5(x+6)+11=25−3x
Step 1: Simplify both sides of the equation.
5(x+6)+11=25−3x
(5)(x)+(5)(6)+11=25+−3x(Distribute)
5x+30+11=25+−3x
(5x)+(30+11)=−3x+25(Combine Like Terms)
5x+41=−3x+25
5x+41=−3x+25
Step 2: Add 3x to both sides.
5x+41+3x=−3x+25+3x
8x+41=25
Step 3: Subtract 41 from both sides.
8x+41−41=25−41
8x=−16
Step 4: Divide both sides by 8.
8x
8
=
−16
8
which of the following functions will return the value of x, rounded to the nearest whole number?question 5 options:a) abs(x)b) fmod(x)c) round(x)d) whole(x)e) sqrt(x
Answers
The function that will return the value of x, rounded to the nearest whole number is option (c) round(x)
This function rounds the value of x to the nearest integer. For example, if x = 3.4, round(x) will return 3, and if x = 3.6, round(x) will return 4.
Option (a) abs(x) returns the absolute value of x, which means it returns the positive value of x regardless of its sign. For example, if x = -3, abs(x) will return 3.
Option (b) fmod(x) returns the remainder of x divided by another number, so it does not round x to the nearest whole number.
Option (d) whole(x) is not a standard math function, so it is unclear what it would do.
Option (e) sqrt(x) returns the square root of x, so it does not round x to the nearest whole number.
Therefore, the correct answer to this question is option (c) round(x).
To know more about function click on below link :
https://brainly.com/question/29533633#
#SPJ11
what number do these base ten blocks show

Answers
on monday, joey finished his math homework in 32 minutes. on wednesday, he finished his math homework in 28 minutes. what percent represents the difference in time joey spent on his homework from monday to wednesday?
Answers
The percentage that refers the difference in time joey spent on his homework from Monday to Wednesday is 12.5%
The term percentage refers a relative value indicating hundredth parts of any quantity.
Here we have given that on Monday, joey finished his math homework in 32 minutes. on Wednesday, he finished his math homework in 28 minutes.
And we need to find the percent represents the difference in time joey spent on his homework from Monday to Wednesday.
Here first we need to find the improvement in time from Monday to Wednesday.
And its simply calculated as,
=> 32–28 = 4 minutes
And then we simply need to calculate the value of 4/32 in terms of percentage.
Then the calculation of the term is written as,
=> (4/32)*100% = 12.5 %
To know more about Percentage here.
https://brainly.com/question/13729841
#SPJ4
a die is rolled and a coin is tossed at the same time. what is the probability of rolling a 2 and the coin landing on tails?
Answers
Answer:
1/12
Step-by-step explanation:
The probability of rolling a two is
P(2) = number of twos/ total
=1/6
The probability of landing on tails
P(tails) = tails/total
=1/2
P(2, tails) = P(2) * P(tails) since they are independent events
= 1/6 * 1/2
=1/12
if the slope of a line is k, and the line passes through the points (0, k 3) and (-3 , 0), what is the value of k
Answers
Answer:
1
Step-by-step explanation:
assuming your points are (0,3) and (-3,0) you would "rise" 3 and "run" 3 to get from one point to the next on a graph, making your rise over run (aka slope) 3/3 which is equal to 1.
The average life of a bread-making machine is 7 years, with a standard deviation of 1 year. Assuming that the lives of these machines follow approximately a normal distribution, find (a) the probability that the mean life of a random sample of 9 such machines falls between 6.4 and 7.2 years;
Answers
the probability that the mean life of a random sample of 9 bread-making machines falls between 6.4 and 7.2 years is: 0.6106.
We can use the central limit theorem to approximate the sampling distribution of the sample mean of bread-making machines, which is also normally distributed with a mean of 7 years and a standard deviation of 1/√9 = 1/3 years.
Then, we need to standardize the values of 6.4 and 7.2 using the formula:
z = (x - μ) / σ
where x is the value of interest, μ is the mean, and σ is the standard deviation.
For 6.4 years:
z1 = (6.4 - 7) / (1/3) = -1.2
For 7.2 years:
z2 = (7.2 - 7) / (1/3) = 0.6
We want to find the probability that the sample mean falls between 6.4 and 7.2 years, which is equivalent to finding the probability that the standardized sample mean falls between z1 and z2.
Using a standard normal distribution table or calculator, we can find the probabilities associated with each z-value:
P(z < -1.2) = 0.1151
P(z < 0.6) = 0.7257
Therefore, the probability that the mean life of a random sample of 9 bread-making machines falls between 6.4 and 7.2 years is:
P(-1.2 < z < 0.6) = P(z < 0.6) - P(z < -1.2) = 0.7257 - 0.1151 = 0.6106
The probability is approximately 0.6106 or 61.06%.
For similar question on probability.
https://brainly.com/question/30846562
SPJ11
HELP ME ASAP 100 POINTS The height of a right square pyramid is multiplied by 6, but the dimensions of the base remain fixed. By what factor is the volume multiplied? A. 3 B. 6 C. 12 D. 36
Answers
Answer:
the answer is 3 b. multiplied by 6
I need help with this assignment and finding the measures and equations

Answers
Answer:
(4x-9)° +(6x+2)° +x° = 180°∠P = 59°∠Q = 104°∠R = 17°Step-by-step explanation:
Given ∆PQR with ∠P = (4x-9)°, ∠Q = (6x+2)°, and ∠R = x°, you want an equation to find x, and the measures of the angles.
EquationThe equation expresses the fact that the sum of angles in a triangle is 180°.
∠P +∠Q +∠R = 180°
(4x -9)° +(6x +2)° +x° = 180°
Solution11x -7 = 180 . . . . . . . . . . . . divide by °, collect terms
11x = 187 . . . . . . . . . add 7
x = 17 . . . . . . . . divide by 11
AnglesThe angle measures are found by substituting for x in the angle expressions:
∠P = (4·17 -9)° = 59°
∠Q = (6·17 +2)° = 104°
∠R = 17°
please helpFind the particular solution: dy a) + 2xy = x dx dy b) (x + 1) dx - 3y =(x + 1)4 x = 0, y=-1/2 x x= 1, y = 16
Answers
A) The particular solution for the first equation is:
y = 1/2
B) The particular solution to the second equation is:
y = 1/7 (x + 1)⁴ + 12/7 (x + 1)⁻³
a) dy/dx + 2xy = x
First, we need to find the integrating factor:
μ(x) = e∫2x dx = eˣ²
Multiplying both sides by the integrating factor, we get:
eˣ² dy/dx + 2xeˣ²y = xeˣ²
Using the product rule, we can simplify the left-hand side as follows:
d/dx (eˣ² y) = xeˣ²
Integrating both sides with respect to x, we obtain:
eˣ²) y = ∫xeˣ² dx = 1/2 eˣ² + C
Thus, the general solution is:
y = 1/2 + Ce⁻ˣ²
To find the particular solution, we can use the initial condition y(0) = 1/2:
1/2 = 1/2 + Ce⁻₀²
C = 0
Therefore, the particular solution is:
y = 1/2
b) (x + 1) dx - 3y = (x + 1)⁴, x = 0, y = -1/2; x = 1, y = 16
First, we need to rearrange the equation in the standard form:
dy/dx + 3y/(x + 1) = (x + 1)³
Next, we need to find the integrating factor:
μ(x) = e∫3/(x + 1) dx = (x + 1)³
Multiplying both sides by the integrating factor, we get:
(x + 1)³ dy/dx + 3(x + 1)² y = (x + 1)⁶
Using the product rule, we can simplify the left-hand side as follows:
d/dx [(x + 1)³ y] = (x + 1)⁶
Integrating both sides with respect to x, we obtain:
(x + 1)³ y = 1/7 (x + 1)⁷ + C
Thus, the general solution is:
y = 1/7 (x + 1)⁴ + C/(x + 1)³
To find the particular solution, we can use the initial conditions:
y(0) = -1/2
y(1) = 16
Substituting these values, we get a system of equations:
C = -1/7
1/7 (2⁴) - 1/7 = 16
C = 12/7
Therefore, the particular solution is:
y = 1/7 (x + 1)⁴ + 12/7 (x + 1)⁻³
Learn more about particular solution:
https://brainly.com/question/29725792
#SPJ4
please answer this math question

Answers
1/2 = 1/2
No need to add anything