Answers
Answer: volume of the cone is 324pi cm^3
Step-by-step explanation:
the volume of the cone is derived by the formula
V= 1/3 pi r^2 h
v= volume of the cone
h= height of the cone
r= radius of the cone
V= 1/3 x pi x 9 x 9 x 12
V= 324pi cm^3
for more information regarding the volume of cone:
https://brainly.com/question/2628385
Step-by-step explanation:
to find the volume use the formula (1/3)πr2h,
\(( \frac{1}{3})h\pi \: r {}^{2} \\ \frac{1}{ 3} \times \pi \times 9 \times 9 \times 12 \\ \frac{1}{3} \times 972\pi \: cm \\ = 324\pi \: cm {}^{3} \)
Related Questions
A square garden has a length of (x+3) ft and a width of (x+2) ft. what is the perimeter and area of the garden?
Answers
Answer:
Perimeter:\(4x+10\) feet
Area:\(x^{2}+5x+6\) feet
Step-by-step explanation:
The perimeter is equal to 2*width +2*length. The width is x+2 and the length is x+3, therefore the perimeter is equal to 2x+4+2x+6 which equals 4x+10.
The area is equal to width*length
(x+3)(x+2)=\(x^{2}+2x+3x+6=x^{2}+5x+6\)
Use the graph to find f(3).
f(3)=

Answers
Answer:
f(3) = -2
General Formulas and Concepts:
Algebra I
Reading a Cartesian Graph Function NotationStep-by-step explanation:
f(3) is simply asking for the y-value when x = 3. According to the graph, when x = 3, y = -2.
Therefore, f(3) = -2
4) What is the total cost (tax and price) on a purchase of $108.50 if the sales tax is 8%?
D) $195.30
A) $86.50
B) $8.68
C) $117.18
Answers
$108.50 X 1.08 = $108.50
A high school softball team needs to raise $915 to cover the cost of new equipment. They decide to have a car wash where they will charge $3 for cars, c, and $5 for trucks or SUVs, t. The combined number of $3 carwashes for cars, c, and $5 carwashes for trucks or SUVs, t, needed can be represented by the equation If only 5 cars are washed, how many trucks or SUVs need to be washed to raise the full $915?
Answers
a) The combined number of $3 carwashes for cars, c, and $5 carwashes for trucks or SUVs, t, needed can be represented by the equation y = c + t.
b) If only 5 cars are washed, the number of trucks or SUVs needed to be washed to raise the full $915 is 180.
What is an equation?An equation is a mathematical statement that shows that two mathematical expressions are equal or equivalent.
Equations use the equation symbol (=) to show the equality of expressions.
The total amount needed for the new equipment = $915
The charge for a car wash per car = $3
The charge for cash wash per truck or SUV = $5
Let the number of cars = c
Let the number of trucks or SUVs = t
Equations:c + t = y... Equation 1
3c + 5t = 915... Equation 2
If the number of cars, c = 5
From equation 2:
3c + 5t = 915
3(5) + 5t = 915
15 + 5t = 915
5t = 900
t = 180
Thus, from equation 2, we can determine that if cars are 5, the trucks or SUVs must be 180 to meet the target.
Learn more about equations at https://brainly.com/question/2972832
#SPJ1
1
At a book fair, a tote bag costs $10 and books cost $7.50 each. You spend a total of $62.50
before taxes. How many books did you buy in addition to one tote bag? Must show work on
separate sheet of paper. *
Answers
Answer:
7 books
Step-by-step explanation:
$62.50 - $10 = $52.50
$52.50 ÷ $7.50 = 7
You bought 7 books.
what is the soloution to the equation 3x+4=7x-4
Answers
Explanation:3x+4=7x-4
-3x -3x
4=4x-4
+4 +4
8=4x
(divide each side by 4)
2=x
Step-by-step explanation:
3x+4=7x-4
add 7x to each side of equation 4x+3x+-7x=-4x+7x+-7x
combine like terms 7x+-7x=0
4+ -4x =-4 +0
4+-4x= -4
add -4 to each side of equation 4+ -4 +-4x=-4+-4
combine like terms -4 +4=0
0+ -4x = -4+ -4
combine like terms -4+-4=-8
-4x =-8
divide each side by-4
x=2
simplifying
x = 2
For the following, find the arc length:
(Use \large \pi=3.14 and round your final answer to the hundredths.)
x=_________
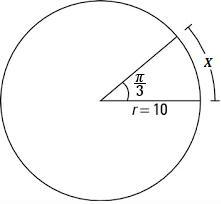
Answers
Answer:
x = 10.47
Step-by-step explanation:
circumference = 2 * 10 * π = 20π
centre angle of a circle (in radiant) = 2π
x : 20π = π/3 : 2π
x = (20π * π/3)/ 2π
x = 10 * π/3
x = 10π/3
x = 10.466667
x = 10.47
Find the value of x
55’. x

Answers
Answer:
x = 35
Step-by-step explanation:
The sum of the angles of a triangle is 180°.
\(x+55+90=180\\x+145=180\\x=35\)
Answer:
\({ \boxed{ \mathfrak{ \: answer : \: { \rm{35\degree}}}}}\)
Step-by-step explanation:
\({ \rm{55 \degree + 90\degree + x = 180\degree}} \\ { \tt{ \{angle \: sum \: of \: a \: triangle \}}} \\ { \rm{145\degree + x = 180\degree}} \\ { \rm{x = 35\degree}}\)
Select all lengths that are equal to 3 yards 16 inches.
Answers
The lengths equal to 3 yards 16 inches are 3 yards, 108 inches, 3.44 yards (approximately), and 108.44 inches (approximately).
To determine the lengths that are equal to 3 yards 16 inches, we need to convert the measurements into a consistent unit. Since both yards and inches are units of length, we can convert the inches into yards or the yards into inches to find the equivalent lengths.
1 yard is equal to 36 inches (since 1 yard = 3 feet and 1 foot = 12 inches).
Therefore, 3 yards is equal to 3 * 36 = 108 inches.
Now, we can compare 108 inches to 3 yards 16 inches.
108 inches is equal to 3 yards, so it matches the given length.
To convert 16 inches into yards, we divide it by 36 since 1 yard = 36 inches. 16 inches / 36 = 0.44 yards.
Therefore, 3 yards 16 inches is equivalent to:
3 yards
108 inches
3 yards 0.44 yards (or approximately 3.44 yards)
108 inches 0.44 yards (or approximately 108.44 inches)
for more such questions on lengths
https://brainly.com/question/28322552
#SPJ8
Jeanine has driven 45 miles of a 240- mile trip.
If she is traveling at or below the 65 mile -per hour speed limit, how much longer can Jeanine expect to spend completing the trip?
Answers
Answer: We can use the formula:
time = distance / speed
to calculate the time it will take Jeanine to complete the trip, assuming she drives at or below the speed limit.
She has already driven 45 miles, so she has 240 - 45 = 195 miles left to travel.
If she drives at 65 miles per hour or less, the maximum speed limit, her travel time will be:
time = distance / speed
time = 195 miles / 65 miles per hour
time = 3 hours
So Jeanine can expect to spend an additional 3 hours completing the trip, assuming she drives at or below the speed limit.
Step-by-step explanation:
A sample of 156 runners is taken from a population of 5300 runners who complete a major marathon.
8. How many runners' times are used to calculate u for the finishing times for this event? Answer choice
5300
34
156
26
Answers
Answer:
4736 because count add them together or do it your way
What is 0.08% written as a decimal?
Answers
A normal population has a mean m=33 and standard deviation s = 9. What is the probability that a randomly chosen value will be greater than 44?
Answers
Answer: 0.1112
Step-by-step explanation:
Let X be a random variable .
Given: A normal population has a mean m=33 and standard deviation s = 9.
The probability that a randomly chosen value will be greater than 44 will be :-
\(P(X>44)=P(\dfrac{X-m}{s}>\dfrac{44-33}{9})\\\\=P(Z>\dfrac{11}{9})\\\\=P(Z>1.22)\\\\ =1-P(Z<1.22)\\\\=1-0.8888\\\\=0.1112\)
Hence, the probability that a randomly chosen value will be greater than 44 = 0.1112
A normal population has a mean m=33 and standard deviation s = 9. the probability that a randomly chosen value will be greater than 44 is - 28.774%
Given:
mean m=33
standard deviation s = 9
probability = ?
Solution:
(34-39)/9 = -0.5556
which mean
34 is -0.5556 standard deviations from the mean.Using the normal distribution table,P(Z<-0.5556) ≈ 0.28774
or 28.774%
Thus, A normal population has a mean m=33 and standard deviation s = 9. the probability that a randomly chosen value will be greater than 44 is - 28.774%
Learn more:
https://brainly.com/question/475676
Find the area of an equilateral triangle with sides of length 24 inches in simplest
form?

Answers
Answer:
B. 144√3 in².
Step-by-step explanation:
Given the following data;
Sides of length = 24 inches
Mathematically, the area of an equilateral triangle is given by the formula;
A = √3 * s²/4
Where, s represents the sides of length.
Substituting into the formula, we have;
A = √3 * 24²/4
A = √3 * 576/4
A = √3 * 144
A = 144√3 in²
6• 2hen+3pens-5anchors
Answers
Answer:
\(180\)
Step-by-step explanation:
\(6 \times 2 \times 3 \times 5\)
\(12 \times 15\)
\(=180\)
Steps to solve:
6 * 2 + 3 - 5
~Multiply
12 + 3 - 5
~Add
15 - 5
~Subtract
10
Best of Luck!
Eric bought a pizza pie, he ate 3/8 of the pie,karla ate 1/4 of the pie ,how much of the pizza did eat
Answers
Answer:
5/8 of the pizza was eaten
Step-by-step explanation:
1/4=2/8
2/8+3/8=5/8
Answer:
5/8
Step-by-step explanation:
3/8 + 1/4
1/4 x 2 = 2/8
3/8 + 2/8 = 5/8
Helppppppppppppp plssssss

Answers
Answer:
Absolute Value = to 0.5 : 0.5
Absolute Value = 5: 5
Absolute Value = 6: 6
Absolute Value = 60: 60
Step-by-step explanation:
Answer:
I'm guessing this is what you need
Step-by-step explanation:

in a certain community, 30% of the families own a dog, 20% of the families that own a dog also own a cat
Answers
Therefore, the probability that a randomly selected family owns a cat is 0.257. Therefore, the conditional probability that a randomly selected family doesn't own a dog given that it owns a cat is 0.778.
What is probability?Probability is a branch of mathematics that deals with the study of random events or situations. It involves the quantification of the likelihood or chance of an event occurring, expressed as a number between 0 and 1, with 0 representing impossibility and 1 representing certainty. The theory of probability provides a framework for making predictions, analyzing data, and making decisions in situations involving uncertainty or randomness.
Here,
Let's use the following events:
D: family owns a dog
C: family owns a cat
From the problem statement, we know:
P(D) = 0.3
P(C|D) = 0.2
P(C) = 0.34
1. To find the probability that a randomly selected family owns a cat, we can use the law of total probability:
P(C) = P(C|D) * P(D) + P(C|not D) * P(not D)
We don't know P(C|not D), but we can find it using the fact that P(not D) = 1 - P(D):
P(C|not D) = (P(C) - P(C|D) * P(D)) / P(not D)
P(C|not D) = (0.34 - 0.2 * 0.3) / (1 - 0.3)
P(C|not D) = 0.2857
Substituting the values:
P(C) = 0.2 * 0.3 + 0.2857 * 0.7
P(C) = 0.257
2. To find the conditional probability that a randomly selected family doesn't own a dog given that it owns a cat, we can use Bayes' theorem:
P(not D|C) = P(C|not D) * P(not D) / P(C)
Substituting the values:
P(not D|C) = 0.2857 * 0.7 / 0.257
P(not D|C) = 0.778
To know more about probability,
https://brainly.com/question/13313866
#SPJ1
Complete question:
In a certain community, 30% of the families own a dog, and 20% of the families that own a dog also own a cat. It is also known that 34% of all the families own a cat. What is the probability that a randomly selected family owns a cat? What is the conditional probability that a randomly selected family doesn't own a dog given that it owns a cat?
An Olympic-size swimming pool holds approximately 6×105 gallons of water. The capacity of this swimming pool is between which interval?
Answers
The capacity of this swimming pool is between B. 500 gallons to 1,000 gallons.
What is the capacity?Capacity refers to the product of the length, width, and height of a three-dimensional object or space.
The capacity of an object means the same as its volume.
Olympic-size swimming pools have the following standard dimensions:
Length = 50 m
Width = 25 m
Height = 2 m
Capacity of an Olympic swimming pool = 2,500 m³ (50 x 25 x 2)
= 660,000 gallons (2,500 x 1,000 ÷ 3.785)
An interval estimate shows the lower and upper limits.
6 x 105 gallons = 630 gallons
Thus, the capacity of the swimming pool is Option B.
Learn more about volume or capacity at https://brainly.com/question/463363
#SPJ1
Question Completion with Answer Options:A. 100 gallons to 500 gallons
B. 500 gallons to 1,000 gallons
C. 1,000 gallons to 1,500 gallons
D. 1,500 gallons to 2,000 gallons
what is the mode for 9,4,4,4,3,2
Answers
Answer:
Mode 4
Step-by-step explanation:
Mean x¯¯¯ 4.3333333333333
Median x˜ 4
Mode 4
Range 7
Minimum 2
Maximum 9
Count n 6
Sum 26
Quartiles Quartiles:
Q1 --> 3
Q2 --> 4
Q3 --> 4
Find x
—3(x – 4) = -9(x - 1)
Answers
Answer:
x=-1/2
Step-by-step explanation:
-3(x-4)= -9(x-1)
-3x+12= -9x+9
-3x+9x= 9-12
6x= -3
x=-3/6
x= -1/2
An engineer has designed a valve that will regulate water pressure on an automobile engine. The valve was tested on 270 engines and the mean pressure was 5.6 pounds/square inch (psi). Assume the population standard deviation is 0.8. The engineer designed the valve such that it would produce a mean pressure of 5.5 psi. It is believed that the valve does not perform to the specifications. A level of significance of 0.02 will be used. Find the value of the test statistic. Round your answer to two decimal places.
Answers
Answer:
The null hypothesis failed to be rejected.
There is not enough evidence to support the claim that the valve pressure is significantly different from 5.5 psi.
P-value = 0.04
Test statistic z=2.05
Step-by-step explanation:
This is a hypothesis test for the population mean.
The claim is that the valve pressure is significantly different from 5.5 psi.
Then, the null and alternative hypothesis are:
\(H_0: \mu=5.5\\\\H_a:\mu\neq 5.5\)
The significance level is 0.02.
The sample has a size n=270.
The sample mean is M=5.6.
The standard deviation of the population is known and has a value of σ=0.8.
We can calculate the standard error as:
\(\sigma_M=\dfrac{\sigma}{\sqrt{n}}=\dfrac{0.8}{\sqrt{270}}=0.049\)
Then, we can calculate the z-statistic as:
\(z=\dfrac{M-\mu}{\sigma_M}=\dfrac{5.6-5.5}{0.049}=\dfrac{0.1}{0.049}=2.054\)
This test is a two-tailed test, so the P-value for this test is calculated as:
\(\text{P-value}=2\cdot P(z>2.054)=0.04\)
As the P-value (0.04) is bigger than the significance level (0.02), the effect is not significant.
The null hypothesis failed to be rejected.
There is not enough evidence to support the claim that the valve pressure is significantly different from 5.5 psi.
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
A volcano on a recently discovered planet rises to a height of 69,657.652 ft.
Use the table of facts to find the height of the volcano in miles.
Round your answer to the nearest tenth.
Answers
Answer:
13.2 miles
Step-by-step explanation:
We can use the following conversion factors:
1 mile = 5,280 feet
Using this conversion, we can divide the height of the volcano in feet by 5,280 to get the height in miles:
69,657.652 ft ÷ 5,280 ft/mi ≈ 13.2 mi
Therefore, the height of the volcano on the recently discovered planet is approximately 13.2 miles.
Hopes this helps
Help! Factoring Bottoms up method:
1. 2x²-9x-18=0
2. 8x²+2x-3=0
3. 5x²-11x+2=0
Answers
In response to the query, we have that Hence, the following are the answers to this equation: 5x - 2 = 0 or x - 1 = 0 Thus, x = 2/5 or x = 1.
What is quadratic equation?A quadratic equation in a single variable is x ax2+bx+c=0, a form of quadratic equation. a 0. The fact that this polynomial is of second sample guarantees that it comprises at least one solution according to the Basic Theorem of Algebra. Solutions might be straightforward or difficult. A quadratic equation is one that has four variables. This suggests that at least single word in it has to be rounded. The formula "ax2 + bx + c = 0" constitutes one of the widely used solutions for complex numbers. where the undefined variable "X" is represented by the numerical values or constants a, b, and c.
2x² - 9x - 18 = 0
Secondly, we must identify two integers whose total is -9 and whose product is 2(-18)=-36. These are the numbers -12 and +3. Hence, we may say:
2x² - 9x - 18 = (2x + 3)(x - 6) = 0
Hence, the following are the answers to this equation:
2x + 3 = 0 or x - 6 = 0
Thus, x = -3/2 or 6.
8x² + 2x - 3 = 0
8x² + 2x - 3 = (4x - 3) (4x - 3)
(2x + 1) = 0
Hence, the following are the answers to this equation:
4x - 3 = 0 or 2x + 1 = 0
Thus, either x = 3/4 or x = -1/2.
5x² - 11x + 2 = 0
5x² - 11x + 2 = (5x - 2)(x - 1) = 0
Hence, the following are the answers to this equation:
5x - 2 = 0 or x - 1 = 0
Thus, x = 2/5 or x = 1.
To know more about quadratic equation visit:
https://brainly.com/question/30098550
#SPJ1
HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
the second one would be the correct anwser i think.
Step-by-step explanation:
Right triangle with a hypotenuse of 159 ft and Angle A = 34 degree
Calculate the length of the sides they should be rounded to the nearest whole foot. The rounded for the legs (side) should be used to calculate the area of the triangle
Answers
the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
Given: The hypotenuse of the right triangle,
c = 159 ft; angle A = 34°
We know that, in a right-angled triangle:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$\)
We know the value of the hypotenuse and angle A. Using trigonometric ratios, we can find the length of sides in the right triangle.We will use the following formulas:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$$$\tan\theta=\frac{\text{opposite}}\)
\({\text{adjacent}}$$\) Length of side a is:
\($$\begin{aligned} \sin A &=\frac{a}{c}\\ a &=c \sin A\\ &= 159\sin 34°\\ &= 91.4 \text{ ft} \end{aligned}$$Length of side b is:$$\begin{aligned} \cos A &=\frac{b}{c}\\ b &=c \cos A\\ &= 159\cos 34°\\ &= 131.5 \text{ ft} \end{aligned}$$\)
Now, we have the values of all sides of the right triangle. We can calculate the area of the triangle by using the formula for the area of a right triangle:
\($$\text{Area} = \frac{1}{2}ab$$\)
Putting the values of a and b:
\($$\begin{aligned} \text{Area} &=\frac{1}{2}ab\\ &=\frac{1}{2}(91.4)(131.5)\\ &= 6006.55 \approx 6007 \text{ sq ft}\end{aligned}$$\)
Therefore, the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
For more question triangle
https://brainly.com/question/29135702
#SPJ8
The tomato plants in Ms. Lang's
garden grow 2 inches every 3 days. How much will they grow in 15 days?
Answers
Answer:
10 inches
Step-by-step explanation:
15 days/3 days =5
5 x 2 =10
Answer the questions below to find the total surface area of the can.

Answers
Answer:
\(\begin{aligned}SA &= 7.125\pi \text{ in}^2\\& \approx 22.4 \text{ in}^2 \end{aligned}\)
Step-by-step explanation:
We can find the Surface Area of the can by adding the areas of each of its parts:
\(SA = 2( A_{\text{base}}) + A_\text{side}\)
First, we can calculate the area of the circular base:
\(A_{\text{circle}} = \pi r^2\)
\(A_{\text{base}} = \pi (0.75 \text{ in})^2\)
\(A_{\text{base}} = 0.5625\pi \text{ in}^2\)
Next, we can calculate the area of the rectangular side:
\(A_\text{rect} = l \cdot w\)
\(A_\text{side} = (4\text{ in}) \cdot C_\text{base}\)
Since the width of the side is the circumference of the base, we need to calculate that first.
\(C_\text{circle} = 2 \pi r\)
\(C_\text{base} = 2 \pi (0.75 \text{ in})\)
\(C_\text{base} = 1.5 \pi \text{ in}\)
Now, we can plug that back into the equation for the area of the side:
\(A_\text{side} = (4\text{ in}) (1.5\pi \text{ in})\)
\(A_\text{side} = 6\pi \text{ in}^2\)
Finally, we can solve for the surface area of the can by adding the area of each of its parts.
\(SA = 2( A_{\text{base}}) + A_\text{side}\)
\(SA = 2(0.5625\pi \text{ in}^2) + 6\pi \text{ in}^2\)
\(\boxed{SA = 7.125\pi \text{ in}^2}\)
\(\boxed{SA \approx 22.4 \text{ in}^2}\)
Which of these values of x is NOT a solution of the equation tanx= 1?

Answers
The tangent ratio is an illustration of the trigonometry identity
The value of x that is not a solution of tan(x) = 1 is 3\(\pi\)/4
How to determine the value that is not a solutionThe trigonometry identity is given as:
tan(x) = 1
Next, we test the x values using a calculator.
When \(x = -7\pi/4\), we have:
tan(-7\(\pi\)/4) = 1
When x = 3\(\pi\)/4, we have:
tan(3\(\pi\)/4) = -1
When x = 5\(\pi\)/4, we have:
tan(5\(\pi\)/4) = 1
When x = \(\pi\)/4, we have:
tan(\(\pi\)/4) = 1
Hence, the value of x that is not a solution of tan(x) = 1 is 3\(\pi\)/4
Read more about trigonometry identity at:
https://brainly.com/question/7331447
