Answers
In this case the length is 12cm, the width is 8cm, and the height is 8cm.
12x8x8 = 768cm
Related Questions
3. Mrs Ofori-Atta's class will be planting a food garden. Here is the plan they have agreed on. a) What is the total area of the food garden in square metres? E. 600 cm 200 cm 200 cm 200 cm 1,000 cm с
Answers
Answer:
2200cm
Step-by-step explanation:
HELP ASAP YES I WILL GIVE BRAINLIEST

Answers
Answer:
magnesium >potassium
Step-by-step explanation:
Magnesium deficiency is frequently associated with hypokalemia. Concomitant magnesium deficiency aggravates hypokalemia and renders it refractory to treatment by potassium. Herein is reviewed literature suggesting that magnesium deficiency exacerbates potassium wasting by increasing distal potassium secretion.
how do I represent a function in tables
Answers
Based on the information in the two-way table, what is the probability that a person
selected at random both bikes and runs?
Round your answer to the nearest tenth of a percent.

Answers
Answer:
Step-by-step explanation:

How many 3/4
cups of juice can be poured from 6 cups of juice?
Answers
Answer:8
Step-by-step explanation: 4x6=28
28 divided by 4 = 8
A standard number cube, labeled numbers 1-6 on each side, is rolled three times. Mary says the chance of rolling a 2 all three times is 1/8. But John disagrees and says the probability for rolling a 2 all three times is 1/216. Who calculated the correct probability or rolling a 2 the three times the n number cube is rolled? Show work to justify your reasoning.
Answers
Answer: john answer it correctly
Step-by-step explanation:
6.6.6_=216
Put the following equation of a line into slope-intercept form, simplifying all fractions. 3y-9x=-6
Answers
Answer: y=3x-2
Step-by-step explanation:
3y-9x=-6
First you will need to add 9x to the other side so your equation will look like 3y=9x-6. Then you need to divide all the numbers by 3. So 3y divided by 3 and 9 divided by 3 and -6 divided by 3. Your final answer should be y=3x-2.
Answer:
This equation in slope intercept form would be y = 3x - 2
Step-by-step explanation:
The following is how to solve this equation:
3y - 9x = -6
+9x +9x
----------------------
3y = 9x - 6
divide each of the numbers by 3
So the answer is y = 3x - 2
A lab technician needs 35 ml of 15% base solution for a certain experiment,
but she has only 10% solution and 20% solution. How many milliliters of
the 10% and the 20% solutions should she mix to get what she needs?
Answers
Answer:
17.5ml- of 10 percent solution, 17.5ml- of 20 percent solution
Step-by-step explanation:
35:100*15=5.25- ml of alkali in the base solution
Suppose we need x ml of 10 percents solution and 35-x - of 20 percents.
Then The quantity of alkali in the first one (10 percents) is x/100*10=0.1x
when in the second one we have (35-x)/100*20= 7-0.2x of alkali
0.1x+7-0.2x=5.25
7-0.1x= 5.25
0.1x=1.75
x=17.5- 0f 10 percents
35-17.5=17.5 - of 20 percents
Tristan is a salesperson who sells computers at an electronics store. He makes a base pay amount each day and then is paid a commission as a percentage of the total dollar amount the company makes from his sales that day. Let
P
P represent Tristan's total pay on a day on which he sells
x
x dollars worth of computers. The table below has select values showing the linear relationship between
x
x and
P
.
P. Determine the percentage commission Tristan makes on his daily sales.

Answers
Answer:
\(m = 1.5\%\)
Step-by-step explanation:
Given
The attached table
Required
Determine his percentage commission
To do this, we need to calculate the slope (m) of the table as follows:
\(m = \frac{P_2 - P_1}{x_2 - x_1}\)
Where
\((x_1,P_1) = (7000,165)\)
\((x_2,P_2) = (7500,172.5)\)
\(m = \frac{P_2 - P_1}{x_2 - x_1}\) becomes
\(m = \frac{172.5 - 165}{7500- 7000}\)
\(m = \frac{7.5}{500}\)
\(m = 0.015\)
Convert to percentage
\(m = 0.015 * 100\%\)
\(m = 1.5\%\)
Hence, his percentage commission is 1.5%
2tablets 3times a day 14 day supply 15 tablets per bottle what is the quantity needed
Answers
6 bottles are required for a 14 day supply.
One bottle contains 15 tablets and the dosage is two tablets thrice daily for 14 days, we need to find the quantity of tablets required. Let's calculate it. Quantity needed We know,
Total tablets required=Tablets required
per day x Days
To find the total tablets required, we first need to find the tablets required per day. Tablets required per day Given that,2 tablets are taken thrice daily,
Therefore the tablets required
per day= 2 x 3 = 6 tablets Per day, 6 tablets are required.
Total tablets required Now we can find the total tablets required by multiplying the tablets required per day by the number of days. Hence,
Total tablets required = Tablets required per day x Days= 6 tablets/day x 14 days= 84 tablets14 day supply has to be made with the given 15 tablets per bottle.
Hence, Quantity needed = Total tablets required/ Tablets per bottle= 84/15 = 5.6 or 6 bottles
For more question Quantity
https://brainly.com/question/29091879
#SPJ8
Please help I'll mark brainliest

Answers
Answer:
I think it should be 80-89.
Because the mode can't be between 70 and 70 that wouldn't make sense. Basically 70 and 70 will equal 0 in between so it wouldn't be the best choice.
Enter the number that belongs in the green box
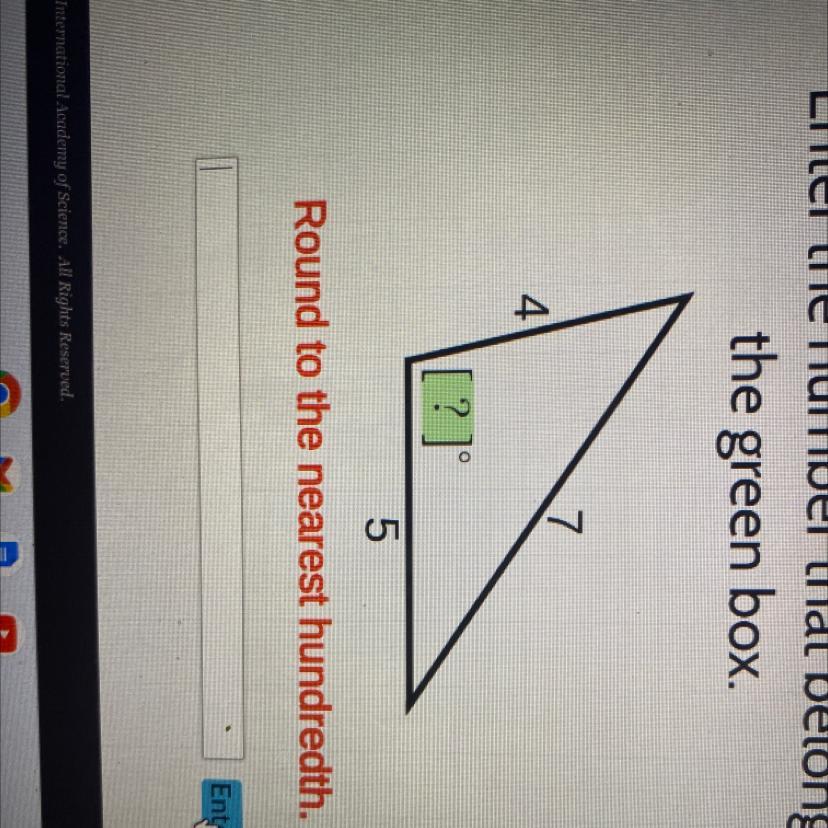
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
Find the slope of the line. Describe how one variable changes in relation to the other. A. 2; distance increases by 2 miles per hour B. 2; distance decreases by 2 miles per hour C. 1/2; distance increases by 1 mile every 2 hours D. 1/2; distance decreases by 1 mile every 2 hours
Answers
The line's slope is \(\frac{1}{2}\) and the distance increases by 1 mile every 2 hours.
What is a good example of a line's slope?
The proportion of the increase in the y-value to the increase in the x-value may also be used to determine slope. For instance: We can get the slope of a line given two locations, P = (0, -1) & Q = (4,1) on the line.
A. Since the line's slope is 2, it follows that the y-variable, which is most likely distance, grows by 2 units for every increment in the x-variable, which is most likely time. The accurate statement is thus: speed is increased by Two miles per hour.
B. Since the line's slope is 2, it follows that the y-variable will drop by 2 units for every unit rise in the x-variable, which is most likely time. The accurate description is thus: speed drops by Two miles per hour.
C. If the line's slope is 1/2, the y-variable will rise by 1/2 unit for every increment in the x-variable, which is probably time. The precise description is that the distance grows by a mile every two hours.
D. If indeed the line's slope is 1/2, the y-variable will drop by 1/2 unit for every unit rise in the x-variable, which is probably time. The precise description is: distance shrinks by a mile every two hours.
To know more about slope of a line visit:
brainly.com/question/16180119
#SPJ9
Evaluate 10c4 and 11p5
Answers
To evaluate permutations and combinations, we use the following formulas:
\(\begin{gathered} nPr=\frac{n!}{(n-r)!} \\ \\ nCr=\frac{n!}{r!(n-r)!} \end{gathered}\)where n is the total number of objects and r is the number of objects selected from the set.
Following the formulas above, we can solve 10C4 and 11P5.
\(\begin{gathered} 10C4=\frac{10!}{4!(10-4)!} \\ \\ 10C4=\frac{10!}{4!\text{ }6!} \\ \\ 10C4=\frac{10\cdot9\cdot8\cdot7\cdot6!}{4\cdot3\cdot2\cdot1\cdot6!} \\ \\ 10C4=10\cdot3\cdot7 \\ \\ 10C4=210 \end{gathered}\)\(\begin{gathered} 11P5=\frac{11!}{(11-5)!} \\ \\ 11P5=\frac{11!}{6!} \\ \\ 11P5=\frac{11\cdot10\cdot9\cdot8\cdot7\cdot6!}{6!} \\ \\ 11P5=11\cdot10\cdot9\cdot8\cdot7 \\ \\ 11P5=55,440 \end{gathered}\)The answers are 210 and 55,440.
Perform the operation. Enter your answer in scientific notation. 7 × 102 − 5.6 × 102 =
Answers
Sadam earns 1.5% commission on homes that he sells. Last month, he sold $3,000,000 worth of homes. How much money did he earn last month?
Answers
Ben starts walking along a path at 2 mi/h. One and a half hours after Ben leaves, his sister Amanda begins jogging along the same path at 7 mi/h. How long (in hours) will it be before Amanda catches up to Ben?
Answers
Answer:
Amanda will catch up Ben after 0.6 hours.
Step-by-step explanation:
Amanda begins jogging along the same path at 7 mi/h.
This means that Amanda's position, after t hours, is given by:
\(A(t) = 7t\)
Ben starts walking along a path at 2 mi/h.
Amanda leaves after one and a half hour, which means that Ben will be at position 2*1.5 = 3. So Ben's position after t hours is given by:
\(B(t) = 3 + 2t\)
How long (in hours) will it be before Amanda catches up to Ben?
This will happen when:
\(A(t) = B(t)\)
So
\(7t = 3 + 2t\)
\(5t = 3\)
\(t = \frac{3}{5}\)
\(t = 0.6\)
Amanda will catch up Ben after 0.6 hours.
It would take Amanda 0.6 hours or 6/10 hours to catch up with Ben.
This question comes from a topic in mathematics called rates and it's used to compare two values with each other and how one value affects the other value.
Let s represent the distance Amanda travels until she meet Ben.
We can set a timer on our phone when she leaves in order to track the time taken.
Let t represent the time taken.
Set of EquationWe can come up with two equations from these scenario
d - 3 = 2t------ equation (i)d = 7t ----- equation (ii)Substitute equation (ii) into equation (i)
\(7t -3 =2t\)
collect like terms
\(7t-2t=3\\5t=3\\t=3/5\\t=0.6\)
From the above, we can see it took her 0.6 hours to catch up with Ben.
Learn more about rates here;
https://brainly.com/question/14323743
In △JKL , if m∠ J < 90° , then ∠K and ∠L are _____
Answers
Both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
In triangle JKL, if angle J is less than 90 degrees, then angle K and angle L are both acute angles.
An acute angle is defined as an angle that measures less than 90 degrees. Since angle J is given to be less than 90 degrees, it is an acute angle.
In a triangle, the sum of the interior angles is always 180 degrees. Therefore, if angle J is less than 90 degrees, the sum of angles K and L must be greater than 90 degrees in order to satisfy the condition that the angles of a triangle add up to 180 degrees.
Hence, both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
For more questions on triangle
https://brainly.com/question/1058720
#SPJ8
The equation of a circle is x² + y²-6y+1=0. What are the coordinates of
the center and the length of the radius of this circle?
(1) center (0,3) and radius 2√2
(2) center (0,-3) and radius 2√2
(3) center (0.6) and radius √35
(4) center (0,-6) and radius √35
Answers
Answer:
center (0, 3) and radius 2√2
Step-by-step explanation:
Equation of a circle
\((x-a)^2+(y-b)^2=r^2\)
where:
(a, b) is the centerr is the radiusGiven equation:
\(x^2+y^2-6y+1=0\)
Subtract 1 from both sides:
\(\implies x^2+y^2-6y=-1\)
To create a trinomial with variable y, add the square of half the coefficient of the y term to both sides:
\(\implies x^2+y^2-6y+\left(\dfrac{-6}{2}\right)^2=-1+\left(\dfrac{-6}{2}\right)^2\)
\(\implies x^2+y^2-6y+9=8\)
Factor the trinomial with variable y:
\(\implies x^2+(y^2-6y+9)=8\)
\(\implies x^2+(y-3)^2=8\)
Factor \(x^2\) to match the general form for the equation of a circle:
\(\implies (x-0)^2+(y-3)^2=8\)
Compare with the general form of the equation for a circle:
\(\implies a=0\)
\(\implies b=3\)
\(\implies r^2=8 \implies r=2\sqrt{2}{\)
Therefore, the center is (0, 3) and the radius is 2√2
What is the volume of the shape below

Answers
The volume of the given figure is 1176 cubic cm.
The value of the figure is calculated by multiplying all three side areas. Volume is a measure of the amount of space that an object or a substance occupies. It is typically expressed in cubic units such as cubic meters (m³), cubic centimetres (cm³), or cubic feet (ft³).
The volume of the figure is calculated as,
Volume = 2 ( 15 x 6 + 20 x 6 + 20 x 18 )
Volume = 1176 Cubic cm
Hence, the volume of the figure will be equal to 1176 Cubic cm.
To know more about volume follow
https://brainly.com/question/29568631
#SPJ1
¿De qué número 64 es el 80%?
Answers
How do you write 9.79 x 101 in standard form
I
Answers
Answer:
Scientific notation: 9.79 × 10^1
Standard form: 97.9
Which percent is equivalent to 2 5/6?
Answers
Answer: 283.3333333% (283.3%)
Step-by-step explanation:
First, lets turn 2 5/6 into and improper fraction. It becomes 17/6.
Now, we divide 17/6
17/6 = 2.833333333
Now, to turn it into a percent, we multiply it by 100, or move the decimal point 2 places to the right. That gives us 283.3333333% (283.3%)
Hope this helps!
Two marbles are drawn in succession from the box containing 10 red, 30 white, 20 blue, and 15 orange marbles. replacement being made after each drawing. Find the probability that is: (a) both are white (b) the first is red and the second is white (c) neither is orange (d) they are either red or white or both ( red and white ) (e) the second is not blue (f) the first is orange (g) at least one is blue (h) at most one is red (i) the first is white but the second is not (j) only one is red
Answers
(a) The probability that both marbles are white is \((30/85) * (30/85) = (\frac{1}{17})^2.\)
(b) The probability that the first is red and the second is white is (10/85) * (30/85) = \((\frac{2}{17})^2\)=0.013
(c) The probability that neither is orange is (1 - 15/85) * (1 - 15/85) = (70/85) * (70/85)=0.67
(d) The probability that they are either red or white or both is (10/85) + (30/85) + (10/85 * 30/85) = (12/17) + (36/289)=0.83
(e) The probability that the second is not blue is 1 - (20/85) = 65/85=0.76
(f) The probability that the first is orange is 15/85=0.17
(g) The probability that at least one is blue is 1 - (65/85 * 64/84) = 51/85=0.6
(h) The probability that at most one is red is (10/85) + (74/85 * 73/84) = (10/85) + (54/289)=0.30
(i) The probability that the first is white but the second is not is (30/85) * (55/84)=0.23
(j) The probability that only one is red is (10/85 * 74/84) + (75/85 * 10/84) = (7/17) + (5/17)=0.70
To learn more about probability, visit:
brainly.com/question/11234923
#SPJ4
HELP please help help

Answers
Answer:
4778.4
Step-by-step explanation:
The volume of a cone is given by:
(π•r²•h)/3
(π•13²•27)/3
(π•169•27)/3
(4,563•π)/3
14,334.66/3=4778.4
=π×13²×27×1/3
=1521π
≈4778.36243
≈4778.4
Hope my answer helped u :)
Find the value of x such that the line containing (1,2) and (5,3) is perpendicular to the line containing (x,4) and (3,0)
Answers
The value of x that makes the line containing (1,2) and (5,3) perpendicular to the line containing (x,4) and (3,0) is x = 2.
To determine the value of x such that the line containing (1,2) and (5,3) is perpendicular to the line containing (x,4) and (3,0), we need to find the slope of both lines and apply the concept of perpendicular lines.
The slope of a line can be found using the formula:
slope = (change in y) / (change in x)
For the line containing (1,2) and (5,3), the slope is:
slope1 = (3 - 2) / (5 - 1) = 1 / 4
To find the slope of the line containing (x,4) and (3,0), we use the same formula:
slope2 = (0 - 4) / (3 - x) = -4 / (3 - x)
Perpendicular lines have slopes that are negative reciprocals of each other. In other words, if the slope of one line is m, then the slope of a line perpendicular to it is -1/m.
So, we can set up the equation:
-1 / (1/4) = -4 / (3 - x)
Simplifying this equation:
-4 = -4 / (3 - x)
To remove the fraction, we can multiply both sides by (3 - x):
-4(3 - x) = -4
Expanding and simplifying:
-12 + 4x = -4
Adding 12 to both sides:
4x = 8
Dividing both sides by 4:
x = 2
For more such questions on line.
https://brainly.com/question/280216
#SPJ8
PLS HELP WILL GIVE BRAINLIEST IVE BEEN ASKING FOREVER :(((((

Answers
Answer:
__C) 0.36
Step-by-step explanation:
4÷11= 0.36363636363636
so it's 0.36 with a line over it indicating a repeating decimal
Please help I am so lost thank you so much

Answers
The speed of the plane is equal to 120 mph.
What is speed?In Mathematics and Geometry, speed is the distance covered by a physical object per unit of time. This ultimately implies that, speed can be measured by using miles per hour (mph).
Mathematically, the speed of any a physical object can be calculated by using this formula;
Speed = distance/time
Time = distance/speed
Let the variable s represent the speed of the plane in miles per hour. Therefore, an equation that models the situation can be written as follows;
240/s = 80/s - 80
80s = 240s - 19200
19200 = 160s
s = 19200/160
s = 120 mph.
Read more on speed here: https://brainly.com/question/29445231
#SPJ1
(2 1/3 x+7)−( 2/3 x+5)
Answers
Answer:
=19/3x+2
Step-by-step explanation:
plz help me, plz help deku!?!

Answers
Answer:
14 cm squared
Step-by-step explanation:
The shaded triangle is clearly half of the rectangle, and half of 28 is 14.
The other way you can look at it is that the dimensions of the rectangle are 4 cm and 7 cm. The area of a triangle equation is \(\frac{bh}{2}\). So \(\frac{4(7)}{2}\) is 14.
Answer:I don’t know sorry deku
Step-by-step explanation:
