Answers
Answer:
x = 50°
Step-by-step explanation:
2x = 140 - 40
2x = 100
x = 100/2
x = 50°
Answer:
D
Step-by-step explanation:
I think its D because you could set up the equation like
40 = 2x
then divide by 2 because of the 2x
Related Questions
neeeeeeeeeeeeeedddddddddddddddddddd will give brain

Answers
Answer:
7
Step-by-step explanation:
11 times 7 =77
Find domain and range of the relation: (-2,7), (-2,6), (-2,5), (-2,4).
Then determine whether the relation of a function (yes or no).
Answers
The domain and range of the relation are { -2 } and { 4, 5, 6, 7 } respectively. The relation is not a function.
Is the relation a function? What are the domain and range?A function is simply a relationship that maps one input to one output, that is, each x-value can only have one y-value.
Given the relation in the question;
(-2,7), (-2,6), (-2,5), (-2,4)
For a relation to be a function, every x-value must have only one y-value mapped to it.
-2 appeared twice and its corresponding y-values are different.
Hence, the relation is Not a Function.
The Domains are the x-values and the Range are the y-values,
Domain: { -2 }
Range: { 4, 5, 6, 7 }
Learn more about functions here: brainly.com/question/2541698
#SPJ1
Part A: Maci made $170 grooming dogs one day with her mobile dog grooming business. She charges $60 per appointment and earned $50 in tips. Write an equation to represent this situation and solve the equation to determine how many appointments Maci had.
Part B: Logan made a profit of $235 as a mobile groomer. He charged $75 per appointment and received $40 in tips, but also had to pay a rental fee for the truck of $10 per appointment. Write an equation to represent this situation and solve the equation to determine how many appointments Logan had.
Answers
Maci and 2 appointments and Logan had 3 appointments.
How many appointments did Maci and Logan have?The linear equation that represents the total amount earned by Maci is:
Total amount earned = (amount per appointment x number of appointments) + tips
$170 = ($60 x a) + $50
$170 = $60a + $50
$170 - $50 = $60a
$120 = $60a
a = $120 / $60
a = 2
The linear equation that represents the total amount earned by Logan is:
Profit = total revenue - total cost
Profit = (fee per appointment x number of appointments) + amount received in tips - (rental fee x number of appointments)
$235 = ($75 x a) + $40 - ($10 x a)
$235 = $75a + $40 - $10a
$235 = $65a + $40
$235 - $40 = $65a
$195 = $65a
a = $195 / 65
a = 3
To learn more about profit, please check: https://brainly.com/question/26181966
#SPJ1
17% of what number is 51
Answers
Answer:
300
Step-by-step explanation:
First five terms of the Recursive sequence

Answers
Answer:
please make me brain
Step-by-step explanation:
option (3) is answer bro
Which other expression has the same value as (-14)-(-8)
Answers
Anytime you are subtracting a negative number, you change it to adding a positive number; a - (-b) = a + b
-14 - (-8) is the same as -14 + 8
-14 + 8 = -6
Best of Luck!
Answer:
(-14) +8
Step-by-step explanation:
I cant solve please help me

Answers
Answer:
Let us set up a ratio to find the relationship between side lengths of the two triangles.
25:10
5:2
We can divide both sides by two, but there's no need as the smaller triangle has multiples of two.
So, if XZ is 6, let's place it into the ratio and find what "x" is.
5(3) : 2(3)
15 : 6
x = 15
Are the equations sometimes, always, or never true? a. 15 + 2x − 4 = 9x + 11 − 7x b. 2x + 3(4x − 1) = 2(5x + 3) + 4x
Answers
Answer:
Step-by-step explanation:
\(15+2x-4=9x+11-7x \rightarrow 2x+11=2x+11\) True for all x.
\(2x+3(4x-1)=2(5x+3)+4x \rightarrow 2x+12x-3=10x+6+4x\)
\(\rightarrow 14x-3=14x+6\)
\(\rightarrow 14x=14x+9\) Cannot be true.
help plssI CANTFAIL OR ELSE I GET EXPELLED

Answers
Based on the dimensions of the parallelogram, it can be concluded its area would be 84 square meters.
How to calculate the area of a parallelogram?The area of a parallelogram can be calculated using the following formula:
Area = base x height
This formula is the same that you would use for calculating the area of a rectangle due to the similarities between these two shapes. Now, let's use the formula to know the area:
Area = 12 meters x 7 meters
Area = 84 square meters
This means the total area is 84 square meters.
Learn more about the area in https://brainly.com/question/27683633
#SPJ1
Which equation represents a line that passes through (5, 1) and has a slope of StartFraction one-half EndFraction?
y – 5 = y minus 5 equals StartFraction one-half EndFraction left-parenthesis x minus 1 right-parenthesis.(x –1)
y – y minus StartFraction one-half EndFraction equals 5 left-parenthesis x minus 1 right-parenthesis. = 5(x –1)
y – 1 = y minus 1 equals StartFraction one-half EndFraction left-parenthesis x minus 5 right-parenthesis.(x –5)
y – 1 = 5y minus 1 equals 5 left-parenthesis x minus StartFraction one-half EndFraction right-parenthesis.
Answers
Step-by-step explanation:
Slope 1/2 point 5,1
in point slope form would be
(y-1) = 1/2 (x-5)
HELLPP PLEASE ASAP!!!!
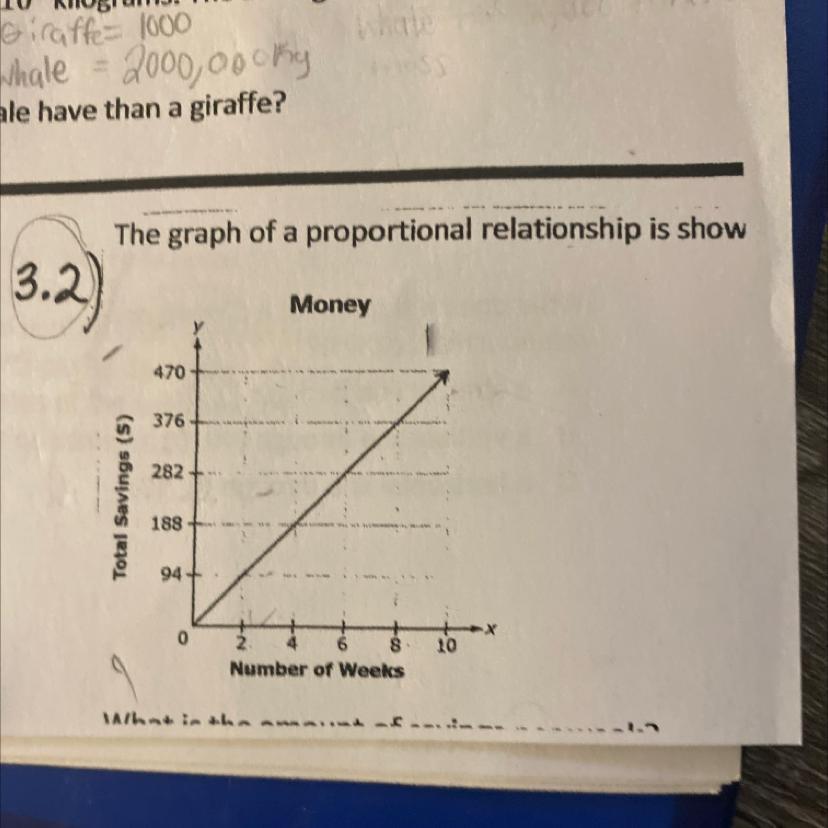
Answers
A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides. Given that there are 30 meters of fencing available, determine the dimensions that would create the garden of maximum area. What is the maximum possible area?
Answers
The dimensions of the garden that create the maximum area are 5 meters by 15 meters, and the maximum possible area is 75 square meters
What is measurement?
Measurement is the process of assigning numerical values to physical quantities, such as length, mass, time, temperature, and volume, in order to describe and quantify the properties of objects and phenomena.
Let's assume that the rock wall is the width of the garden and the wire fencing is used for the length and the other two sides. Let's denote the length of the garden as L and the width as W.
Since we have 30 meters of fencing available, the total length of wire fencing used is:
L + 2W = 30 - W
Simplifying this equation, we get:
L = 30 - 3W
The area of the garden is:
A = LW
Substituting the expression for L from the previous equation, we get:
A = W(30 - 3W)
Expanding the expression, we get:
A = 30W - 3W²
To find the maximum area, we need to take the derivative of A with respect to W and set it equal to zero:
dA/dW = 30 - 6W = 0
Solving for W, we get:
W = 5
Substituting this value back into the expression for L, we get:
L = 15
Therefore, the dimensions of the garden that create the maximum area are 5 meters by 15 meters, and the maximum possible area is:
A = 5(15) = 75 square meters
To know more about measurement visit:
brainly.com/question/4804936
#SPJ1
Oliver did the high jump three times. His scores were 7.016 feet, 5.42 feet, and 8.308 feet. How many feet did he jump in total? pleas help im in test
Answers
The total height of the three jumps is A = 20.744 feet
Given data ,
1st high jump score: 7.016 feet
2nd high jump score: 5.42 feet
3rd high jump score: 8.308 feet
On adding the scores , we get
7.016 + 5.42 + 8.308 = 20.744 feet
On simplifying the equation , we get
A = 20.744 feet
Hence , Oliver jumped a total of 20.744 feet in the three high jumps
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
What is the solution set?

Answers
Answer: x = 1 so 1/2 - 4/1 + 8 = 0n
Step-by-step explanation:
Answer:
- 1.45
Step-by-step explanation:
nth term for 300,250,200
Answers
The nth term of the arithmetic sequence 300,250,200 is 350-50n if the common ratio is -50
What is a sequence?It is defined as the systematic way of representing the data that follows a certain rule of arithmetic.
We have an arithmetic sequence:
300,250,200
The first term a = 300
Common difference d = 250-300 = -50
nth term:
A(n) = a + (n-1)d
A(n) = 300 + (n-1)(-50)
A(n) = 300 -50n + 50
A(n) = 350—50n
Thus, the nth term of the arithmetic sequence 300,250,200 is 350-50n if the common ratio is -50
Learn more about the sequence here:
brainly.com/question/21961097
#SPJ1
A survey found that women's heights are normally distributed with mean 63.6 in and standard deviation 2.5 in. A branch of the military requires women's heights to be between 58 in and 80 in.
a. Find the percentage of women meeting the height requirement. Are many women being denied the opportunity to join this branch of the military because they are too short or too tall?
b. If this branch of the military changes the height requirements so that all women are eligible except the shortest 1% and the tallest 2%, what are the new height requirements?
Answers
Answer:
(A)
Step-by-step explanation:
The survey follows of women's height a normal distribution.
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
The new height requirements would be 57.7 to 68.6 inches
The given parameters are:
\mathbf{\mu = 63.5}μ=63.5 --- mean
\mathbf{\sigma = 2.5}σ=2.5 --- standard deviation
(a) Percentage of women between 58 and 80 inches
This means that: x = 58 and x = 80
When x = 58, the z-score is:
\mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
This gives
\mathbf{z_1= \frac{58 - 63.5}{2.5}}z
1
=
2.5
58−63.5
\mathbf{z_1= \frac{-5.5}{2.5}}z
1
=
2.5
−5.5
\mathbf{z_1= -2.2}z
1
=−2.2
When x = 80, the z-score is:
\mathbf{z_2= \frac{80 - 63.5}{2.5}}z
2
=
2.5
80−63.5
\mathbf{z_2= \frac{16.5}{2.5}}z
2
=
2.5
16.5
\mathbf{z_2= 6.6}z
2
=6.6
So, the percentage of women is:
\mathbf{p = P(z < z_2) - P(z < z_1)}p=P(z<z
2
)−P(z<z
1
)
Substitute known values
\mathbf{p = P(z < 6.6) - P(z < -2.2)}p=P(z<6.6)−P(z<−2.2)
Using the p-value table, we have:
\mathbf{p = 0.9999982 - 0.0139034}p=0.9999982−0.0139034
\mathbf{p = 0.9860948}p=0.9860948
Express as percentage
\mathbf{p = 0.9860948 \times 100\%}p=0.9860948×100%
\mathbf{p = 98.60948\%}p=98.60948%
Approximate
\mathbf{p = 98.61\%}p=98.61%
This means that:
The height of 98.51% of women that meet the height requirement are between 58 inches and 80 inches.
So, many women (outside this range) would be denied the opportunity, because they are either too short or too tall.
(b) Change of requirement
Shortest = 1%
Tallest = 2%
If the tallest is 2%, then the upper end of the shortest range is 98% (i.e. 100% - 2%).
So, we have:
Shortest = 1% to 98%
This means that:
The p values are: 1% to 98%
Using the z-score table
When p = 1%, z = -2.32635
When p = 98%, z = 2.05375
Next, we calculate the x values from \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
Substitute \mathbf{z = -2.32635}z=−2.32635
\mathbf{-2.32635 = \frac{x - 63.5}{2.5}}−2.32635=
2.5
x−63.5
Multiply through by 2.5
\mathbf{-2.32635 \times 2.5= x - 63.5}−2.32635×2.5=x−63.5
Make x the subject
\mathbf{x = -2.32635 \times 2.5 + 63.5}x=−2.32635×2.5+63.5
\mathbf{x = 57.684125}x=57.684125
Approximate
\mathbf{x = 57.7}x=57.7
Similarly, substitute \mathbf{z = 2.05375}z=2.05375 in \mathbf{z= \frac{x - \mu}{\sigma}}z=
σ
x−μ
\mathbf{2.05375= \frac{x - 63.5}{2.5}}2.05375=
2.5
x−63.5
Multiply through by 2.5
\mathbf{2.05375\times 2.5= x - 63.5}2.05375×2.5=x−63.5
Make x the subject
\mathbf{x= 2.05375\times 2.5 + 63.5}x=2.05375×2.5+63.5
\mathbf{x= 68.634375}x=68.634375
Approximate
\mathbf{x= 68.6}x=68.6
Hence, the new height requirements would be 57.7 to 68.6 inches
Three (3) is a common factor of 21 and 22.
O A. True
B. False
SUBMIT
Answers
Answer:
false.
Step-by-step explanation:
Factors for 21: 1, 3, 7, and 21. Factors for 22: 1, 2, 11, and 22.
Answer:
B false
hello hope this helps
which of the following are problematic tendencies we have in reasoning that, according to the text and lecture, can be diminished by thinking in terms of degrees of confidence rather than binary belief?
Answers
The problematic tendencies that can be diminished by thinking in terms of degrees of confidence rather than binary belief are overconfidence and bias.
Habits, behaviors, or mental patterns that are problematic or undesired and have the potential to produce bad results or issues are known as problematic inclinations. Thinking about degrees of confidence allows one to adopt a more complicated and probabilistic approach to decision-making by considering the information's uncertainty and complexity.
According to the text and lecture, focusing on confidence levels rather than having a strong or weak conviction might assist reduce negative reasoning tendencies like overconfidence in one's beliefs and actions, overgeneralization and oversimplification of complicated situations. Confirmation bias is the practice of selectively seeking out and interpreting data in a way that confirms one's preexisting ideas, and belief persistence is the practice of refusing to change one's beliefs in the face of new evidence.
Read more about tendencies on:
https://brainly.com/question/14618657
#SPJ4
9.2384E6 in standard form
Answers
Answer:3.294. Hope this helps!
Step-by-step explanation:
a) You have a piece of string that is 36m long. find the areas of all the shapes you can make which have a perimeter of 36m. b) A piece of land has an area of 100m². How many meters of wire fencing is needed to enclose it?
Answers
a. The areas of the square is 81m² and for rectangle is 72m²
b. The perimeter of the square is 40m
What are the areas of all the shapes you can make which have a perimeter of 36m?a. To determine the area of the shapes in which we have that have a perimeter of 36m, we can consider rectangle and square.
For a square;
Perimeter of square = 4L
36 = 4L
L = 9m
The area of the square will be L² = 9² = 81m²
For a rectangle;
The perimeter of rectangle is;
P = 2(L + W)
We can assume that two numbers which will represent the length and width are;
L = 12m, W = 6m or L = 6m, W = 12m
A = 12 * 6 = 72m²
b.
The area of the wire is 100m², the perimeter for this can be calculated when we consider square and rectangle;
Perimeter of square = 4L
Area of square = L² = 100m²
L = 10m
The perimeter of the wire is 4(10) = 40m
Learn more on perimeter and area of rectangle and square here;
https://brainly.com/question/25292087
#SPJ1
when solving |5k+6|=39 what two equations would we set up to allow us to get rid of the absolute value bars?

Answers
Answer:
A
Step-by-step explanation:
In order to get rid of the absolute value bars we would need to put the number outside of the absolute value bars into two signs. One is going to be positive and one is going to be negative. So in this case, the two equations would be 5k+6=39 and 5k+6=-39
Answer all questions please

Answers
Answer:
a) f(1) = 3
b) f(-1) = -0.25
c) x = 0, 3
d) x = -0.75
e) domain [-2, 4]
range [-1, 3]
Step-by-step explanation:
In this graph, f(x) is represented by the y-axis.
a) We can see that f(1) (the y-value when x = 1) is 3.
b) Looking at the graph, we can estimate f(-1) as about -0.25.
c) We need to find the x-values when the y-axis is at 1. We can see that there are two points at x = 0, 3.
d) Looking at the graph, we can estimate that f(x) = 0 around when x = -0.75.
e) The domain of a function is its set of x-values. We can see that f(x) spans from x = -2 to x = 4. That range in interval notation is: [-2, 4]
The range of a function is its set of y-values. We can see that f(x) spans from y = -1 to y = 3. That range in interval notation is: [-1, 3].
The equation of a circle centered at the origin with a radius of unit length is x2 + y2 = 1. This equation changes if the center of the circle is not located at the origin or the radius is not of unit length. You will use the GeoGebra geometry tool to examine how the equation of a circle changes as you move the center and change the radius. Go to equation of a circle , and complete each step below. If you need help, follow these instructions for using GeoGebra.How does the equation change when the radius changes? Unlike h and k, why is r always positive?
Answers
Given the unitary circle equation centered at the origin:
\(x^2+y^2=1\)If the circle is not centered at the origin, but at the point (h, k), the equation becomes:
\((x-h)^2+(y-k)^2=1\)When h = k = 0, we have the particular case of a circle centered at the origin. Now, if the circle is not unitary, the equation becomes:
\(x^2+y^2=r^2\)So when the radius is 1 (unitary circle), we have our initial case. Combining these results, the general equation of a circle of radius r and centered at (h, k) is:
\((x-h)^2+(y-k)^2=r^2\)r is always positive because it represents the measure of the radius length, and the length is always positive. On the other hand, the equation always represents a positive value, because the square of any number is always positive (or zero).
Pls help i don’t know how to do this

Answers
Using the altitude or leg rule, we have:
x ≈ 42.7
y = 40
z ≈ 53.4
How to Apply the Altitude or Leg Rule?The leg rule is given as:
hypotenuse/leg = leg/part.
The altitude rule is:
left/altitude = altitude/right
To find the value of x, apply the altitude rule:
left = x
right = 24
altitude = 32
Substitute:
x/32 = 32/24
Cross multiply:
24x = 32²
24x = 1,024
x ≈ 42.7
To find y, apply the leg rule:
leg = y
part = 24
hypotenuse = x + 24 = 42.7 + 24 = 66.7
Substitute:
66.7/y = y/24
y² = 1,600.8
y = √1x00.8
y = 40
To find z, apply the leg rule:
leg = z
part = x = 42.7
Hypotenuse = 66.7
Substitute:
66.7/z = z/42.7
z² = 2,848.09
z = √2,848.09
z ≈ 53.4
Learn more about the leg or altitude rule on:
https://brainly.com/question/26257841
#SPJ1
Car = V-8 sedan
Years driven = first and second
Miles driven = 15.500 miles first year and 14,500 miles second year
The cost of depreciation will be $
Answers
Answer:
$500
Step-by-step explanatioThe numberber of years driven is the first and second year
= 2
Miles driven
First year= 15,500
Second year= 14,500
Therefore the cost of depreciation can be calculated as follows
15,500-14,500/2
= 1000/2
= 500
Hence the cost of depreciation is $500
The answer is: 2,318
First year on the graph: 8.5
Second year on the graph: 6.9
First year:
15,500 x 8.5 = 131,750
131,750/100 = 1,317.50
Second year:
14,500 x 6.9 = 100,050
100,050/100 = 1,000.50
1,317.50 + 1,000.50 = 2,318

How many planes appear in this figure? Name three points that are collinear. Are points a, b, c, and d coplanar? Explain. At what does and ca interest db

Answers
Determine the value of each. Round all answers to the nearest hundredth
AC =
a=
0=

Answers
The values for the length AC and the angles of the right-angled triangle ABC are AC = 12.37, α = 75.96 , and θ = 14.04 using the trigonometric ratios of tangent.
What is trigonometric ratios?The trigonometric ratios is concerned with the relationship of an angle of a right-angled triangle to ratios of two side lengths. The basic trigonometric ratios includes;
sine, cosine and tangent.
Considering the right-angled triangle ABC, we shall calculate for the angle B and side lengths a and b as follows:
AC² = 3² + 12² {Pythagoras rule}
AC = √(9 +144)
AC = √153
AC = 12.3693
tanα = 12/3 {opposite/adjacent}
α = tan⁻¹(4) {cross multiplication}
α = 75.9638
tanθ = 3/12 {opposite/adjacent}
θ = tan⁻¹(1/4){cross multiplication}
θ = 75.9638
Therefore, the values for the length AC and the angles of the right-angled triangle ABC are AC = 12.37, α = 75.96 , and θ = 14.04 using the trigonometric ratios of tangent.
Know more about trigonometric ratios here: https://brainly.in/question/1165363
#SPJ1
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
(A) Triangle ABC, and triangle QPR are similar based on side-side-side (SSS) similarity.
(B) Triangle ABC and triangle DEF are similar based on side-side-side (SSS) similarity.
(C) ) Triangle STU and triangle JPM are similar based on side-angle-side (SAS) similarity.
(D) ) Triangle SMK and triangle QTR are similar based on angle-angle (AA) similarity.
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths.
The triangle similarity criteria are:
AA (Angle-Angle)SSS (Side-Side-Side)SAS (Side-Angle-Side)(A) Triangle ABC, and triangle QPR are similar based on side-side-side similarity.
12/8 = 9/6
1.5 = 1.5
(B) Triangle ABC and triangle DEF are similar base on side-side-side similarity as shown in the side lengths.
(C) ) Triangle STU and triangle JPM are similar base on side-angle-side similarity.
14/10 = 21/15
1.4 =
(D) ) Triangle SMK and triangle QTR are similar base on angle-angle similarity.
SMK = 90⁰, 60⁰, 30⁰
QTR = 90⁰, 30⁰, 60⁰
Learn more about similar triangles here: brainly.com/question/27996834
#SPJ1
(7-b)+(3b+2)+(7-b)+(3b+2)
Plz help me out I’m a lil stressed out with school
Answers
Answer:
4b+18
Step-by-step explanation:

Answer:
4b+18
Step-by-step explanation:
Urgent help!
A sum of 7500 is invested at a rate of 6.2%per year compounded semi-annually.
After what period of time will the investment amount to $22,000
This is using the equations A=p(1+r/n)^nt and A=Pe^rt
Answers
Using the formula of compound interest, the time taken is 17.63 years
What is compound interestCompound interest refers to the interest that's calculated on both the initial principal and the accumulated interest of a deposit or investment. In other words, it's interest earned not only on the principal amount, but also on the interest earned in previous periods.
Using the formula given and attached to the question;
A = P(1 + r/n)^nt
Substituting the values into the formula;
22000 = 7500(1 + 0.062/2)^(2*t)
solving for t;
t = 17.625 years
Learn more on compound interest here;
https://brainly.com/question/24274034
#SPJ1
