Find the value of x. PLEASE HELP - test tomorrow
The answer is 39.
I need to show my work.
THANK YOU!!!!!

Answers
Answer:
39
Step-by-step explanation:
b+25+296=360
b+321=360
b=360-321
b=39
Related Questions
if it takes 6 men 25 hours to dig 5 holes, how many hours does it take to dig 5 holes with 10 men
Answers
Answer: Answer is 15 hours
Step-by-step explanation:Given 6 men dig 5 holes in 25 hours
Therefore 10 men will take to dig 5 holes is
workers(1) × time(1) = workers(2)×time(2)
(This formula is used when Total work is same)
where workers(1)= 6 men
Time (1) = 25 hours
workers (2) = 10 men
We have find out Time(2)=T(2)
by applying above formula
6×25=10×T2
after simplify
T2= 15 hours
How could Marc mathematically try to prove that he hit the ball near the top of the tower?While on the golf course last weekend Marc hit into the rough, landing the ball behind a tall tree. To get out of the scenario, his best option was to hit the ball high enough so it goes over the tree and hopefully comes down in the fairway for his next shot. So with a mighty swing, he hit the ball into the air and was surprised to see it hit near the top of a 300 foot tall tower that he had not noticed. The formula for this shot is h(x) = -16xsquared + 120x , where h is the height of the ball and x is the number of seconds the ball is in the air. How could Marc mathematically try to prove that he hit the ball near the top of the tower?While on the golf course last weekend Marc hit into the rough, landing the ball behind a tall tree. To get out of the scenario, his best option was to hit the ball high enough so it goes over the tree and hopefully comes down in the fairway for his next shot. So with a mighty swing, he hit the ball into the air and was surprised to see it hit near the top of a 300 foot tall tower that he had not noticed. The formula for this shot is h(x) = -16xsquared + 120x , where h is the height of the ball and x is the number of seconds the ball is in the air. How could Marc mathematically try to prove that he hit the ball near the top of the tower?
Answers
Answer:
To mathematically prove that Marc hit the ball near the top of the tower, he could use the equation h(x) = -16x^2 + 120x, where h is the height of the ball and x is the number of seconds the ball is in the air.
First, Marc would need to determine the maximum height the ball reached during its flight. This can be found by using the vertex formula, which is x = -b/2a. In this case, a = -16 and b = 120, so x = -120/(2*-16) = 3.75 seconds.
Next, Marc can substitute this value back into the original equation to find the maximum height the ball reached. h(3.75) = -16(3.75)^2 + 120(3.75) = 135 feet.
Since the tower is 300 feet tall, Marc could conclude that if the ball hit near the top of the tower, it would have reached a height close to 300 feet. Since the ball reached a maximum height of 135 feet, it is unlikely that it hit the top of the tower.
However, this calculation assumes that the tower is directly in line with Marc's shot and that the ball did not have any horizontal movement. In reality, the tower could have been to the left or right of the shot, and the ball could have had some horizontal movement, which would affect its height at impact. Therefore, this calculation can only provide a rough estimate and cannot definitively prove whether or not the ball hit near the top of the tower.
help on this? please n thank you

Answers
Answer:
Step-by-step explanation:
The lines are parallel. The angles marked are exterior angles on the same side of the transversal. That means they are supplementary.
8x + 12x = 180 Combine
20 x = 180 Divide by 20
20x/20 = 180/20
x = 9
8x = 8 * 9 = 72
12x = 12*9 = 108 Add (just to check)
Total 180 Which is exactly what it should be.
Here is Takeshi's work determining a third point on the graph of an exponential function, `h(x)`.
Explain why the work is incorrect.

Answers
Answer:
Step-by-step explanation:
Let h(x) = y
The exponentail function is of the form :
\(y = ab^x\)
We have :
\(y_{_1} = ab^{x_{_1}}\\y_{_2} = ab^{x_{_2}}\\\\\implies \frac{y_{_1}}{y_{_2}} = \frac{ab^{x_{1}}}{ab^{x_{2}}} \\\\\implies \frac{y_{_1}}{y_{_2}} = \frac{b^{x_{1}}}{b^{x_{2}}} \\\\\implies \frac{y_{_1}}{y_{_2}} = b^{(x_1-x_2)}\)
Given points : (4, 9) and (5, 34.2)
We have:
\(\frac{34.2}{9} = b^{(5-4)}\\\\\implies 3.8 = b\)
Writing the equation with x, y and b:
\(y = ab^x\\\\\implies 9 = a(3.8^4)\\\\a = \frac{9}{3.8^4} \\\\a = 0.043\)
a = 0.043
b = 3.8
When x = 6, y will be:
\(y = (0.043)(3.8^6)\\\\y = 128.47\)
This is not the y value in the question y = 59.4
Therefore (6, 59.4) does not lie on the graph h(x)
In a pre algebra class containing 43 students, there are 4 freshman, 35 sophomores, and 4 juniors. what fraction of the class are sophomores
Answers
The fraction of the class that is sophomores is \(35/43\).
The fraction of the class that is sophomores, divide the number of sophomores by the total number of students in the class.
Number of sophomores = 35
Total number of students = 43
Fraction of sophomores = (Number of sophomores)/(Total number of students Fraction of sophomores)
Fraction of sophomores \(= 35 / 43\)
Therefore, the fraction of the class that are sophomores is = \(35/43\).
To learn more about Fraction here,
https://brainly.com/question/10354322
Determine if the equation given in slope-intercept form represents the graph. If the equation is correct support your reasoning with why it is correct. If the equation is incorrect, give the correct slope-intercept form equation explaining how you determined it.

Answers
The equation given in slope-intercept form does not represent the graph because the y-intercept of the graph is equal to 4 while the y-intercept of the equation is equal to 5.
What is the slope-intercept form?In Mathematics, the slope-intercept form of a line can be calculated by using this linear equation:
y = mx + c
Where:
m represents the slope.c represents the y-intercept.x and y are the data points.What is y-intercept?In Mathematics, the y-intercept of any graph such as a linear function, generally occur at the point where the value of "x" is equal to zero (x = 0).
Based on the information provided regarding the equations and graphs, the y-intercept are as follows:
The y-intercept of y = 4x + 5 is equal to 5.The y-intercept of this graph with point (0, 4) is 4.Read more on y-intercept here: brainly.com/question/19576596
#SPJ1

18% commission on a $500 couch
bro can someone pleaseee help me
Answers
please help me on this im confused please ty

Answers
The domain of the graph of the exponential function is (d) all real numbers
Calculating the domain of the graphFrom the question, we have the following parameters that can be used in our computation:
The graph of the exponential function
The rule of an exponential function is that
The domain is the set of all real numbers
This means that the input value can take all real values
However, the range is always greater than the constant term
From the graph, the constant term is 0
So, the range is y > 0
Read more about domain at
brainly.com/question/27910766
#SPJ1
Please ANSWER!!!!!!!

Answers
Answer:
See explanation
Step-by-step explanation:
It appears that the second graph is better since it seems to be rather consistent. The graph of the first one seems out of place. Therefore it seems to be confusing and could be misleading.
someone please help with my geometry
Answers
Geometry encompasses various topics such as angles, lines, triangles, circles, polygons, and more.
Whether you need help with a specific theorem, a geometric proof, or solving a particular problem, feel free to describe the problem or provide any relevant information.
You can also ask general questions about geometry concepts or seek clarification on any topic you find challenging. Remember to provide all the necessary details, such as given information, diagrams, or specific requirements of the problem, to help me understand and assist you better.
Geometry often involves visual representation, so if you can provide any diagrams or illustrations related to your question, it would be helpful. However, if you can only describe the problem or concept in words, that's perfectly fine too.
Rest assured that I'll do my best to provide clear explanations, step-by-step solutions, and any additional information or insights to help you understand and solve your geometry problem.
For more such questions on Geometry visit:
https://brainly.com/question/24375372
#SPJ8
Find the degree of this polynomial.
-7d
Answers
Hey there!
The degree is the exponent.
Let me explain with examples.
Suppose we have a polynomial 4d.
Its degree is 1 (it's a first degree polynomial)
What is the degree of the polynomial 4d²?
That's right, this is a second-degree polynomial.
And so on...
Let's look at our polynomial.
We have
-7d.
What is the degree of the polynomial?
That's right, 1.
Hence, -7d is a
\(\boxed{\boxed{\bold{first-degree~polynomial}}}\)
Hope everything is clear.
Let me know if you have any questions!
#KeepLearning
\(\bold{Don't~give~up...}\)
If mLNK=(5x-27) and mKNM=(10x-3), find JNM

Answers
The value of \(m\angle JNM=43^{\circ}.\)
According to the question, \(m\angle LNK = (5x-27)^{\circ}, m\angle KNM = (10x-3)^{\circ}.\)
Also we can say that LM is a straight line.
We know, angles on a straight line add up to 180°.
So, \(m\angle LNK+ m\angle KNM = 180^{\circ}\)
⇒\((5x-27)^{\circ}+(10x-3)^{\circ}=180^{\circ}\)
⇒15x-30=180
⇒15x=180+30
⇒15x=210
⇒x=14.
We know, vertically opposite angles are equal.
Here, \(\angle LNK, \angle JNM\) are vertically opposite angles.\(m\angle JNM = m\angle LNK = (5x-27)^{\circ} = (5\times 14 -27)^{\circ}= 43^{\circ}.\)
Hence the measure of \(\angle JNM\) is \(43^{\circ}.\)
To learn more about angles,
https://brainly.com/question/24607467
https://brainly.com/question/28769265
I need help with the problem i sent via screen shot. Please see attatchment. Thaks

Answers
The first step is to find the equations of the lines in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept.
In the solid line, two points on the line are located at: (0,4) and (3,1).
The slope of a line is given by the following formula:
\(\begin{gathered} m=\frac{y2-y1}{x2-x1} \\ By\text{ replacing the known values} \\ m=\frac{1-4}{3-0}=\frac{-3}{3}=-1 \end{gathered}\)And the y-intercept is at y=4. Then b=4.
The equation of the solid line is then:
\(y=-1x+4=-x+4\)As the shaded region is below the line, then we can say that it is represented by the values that are less or equal to the line, then the first inequality is:
\(y\le-x+4\)Now, let's find the equation of the dotted line.
Two points on this line are (0,0) and (3,1).
The slope of this line is:
\(m=\frac{1-0}{3-0}=\frac{1}{3}\)And the y-intercept is at y=0, then b=0.
The equation of the dotted line is then:
\(y=\frac{1}{3}x+0=\frac{x}{3}\)As the shaded region is over the dotted line (the dotted line means the line is not included in the solution), then the shaded region is related to the values which are greater than the line, thus the inequality is:
\(y>\frac{x}{3}\)Therefore, the system of inequalities that represent the shaded portion of the graph is:
\(\begin{gathered} y\le-x+4 \\ y>\frac{x}{3} \end{gathered}\)What is the value of x in the equation 1/5x - 2/3y = 30, when y = 15?
o 4
8
80
200
Answers
Answer:
x = 200
Step-by-step explanation:
1/5x - 2/3y = 30 y = 15
1/5x - 2/3(15) = 30
1/5x - 10 = 30 | + 10
1/5x = 40 | * 5
200 = x
Help me pleaseeeeeee
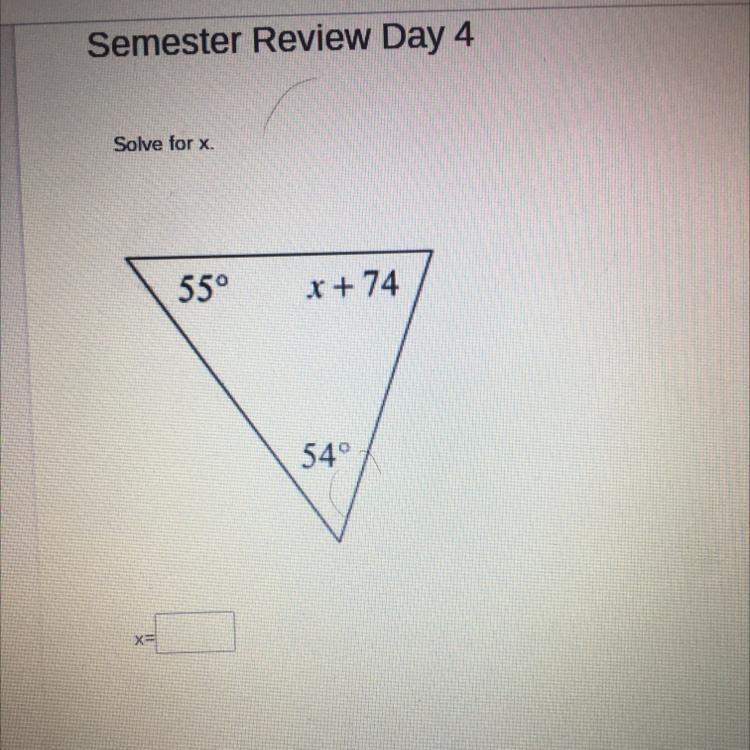
Answers
Answer:x = 54
Step-by-step explanation:
Help please I need asap

Answers
Answer: -120
Step-by-step explanation:
\(2\sum^{4}_{p=1} (p^{2}-9p)=2[(1^{2}-9(1))+(2^{2}-9(2))+(3^{2}-9(3))+(4^{2}-9(4))]=\boxed{-120}\)
Two researchers make a test concerning standardized exam performance among senior high school students in one of two local communities. Researcher A tests performance from the population in the northern community, where the standard deviation of test scores is 110 ( ); Researcher B tests performance from the population in the southern community, where the standard deviation of test scores is 60 ( ). All other things being equal, which researcher has more power to detect an effect? Explain.
Answers
Answer:
Researcher B
Step-by-step explanation:
Normally, when all other things being equal, we usually say that power is higher when the standard deviation is small than when it is large.
Now, from researcher A, standard deviation is 110 while from researcher B, standard deviation is 60.
We can see that the standard deviation for researcher B is smaller than that of researcher A.
Therefore, we can conclude that since the standard deviation for researcher B is lesser than that of researcher A, it means that Researcher B will have more power to detect an effect.
The plot below shows the amount of time Mira spent on
5
55 math problems.
All measurements are rounded to the nearest
1
4
4
1
start fraction, 1, divided by, 4, end fraction minute.
A line plot labeled Time per problem (minutes) shows, moving left to right, labeled tick marks at seven, seven and a half, eight, eight and a half, nine, nine and a half, and ten. An unlabeled tick mark appears between each labeled tick mark. Dots are plotted as follows: 2 dots above the unlabeled tick mark between eight and eight and a half and 3 dots above nine and a half.
A line plot labeled Time per problem (minutes) shows, moving left to right, labeled tick marks at seven, seven and a half, eight, eight and a half, nine, nine and a half, and ten.
If Mira had spent the same total amount of time, but spent an equal amount of time on each problem, how many minutes would each problem have taken?
Answers
If Mira had spent the same total amount of time but an equal amount of time on each problem, each problem would have taken around 2.36 minutes.
In the given plot, Mira spent varying amounts of time on each of the 55 math problems. To find out how many minutes each problem would have taken if Mira had spent an equal amount of time on each problem, we need to calculate the total time she spent and divide it by the number of problems.
Looking at the plot, we can estimate the total time Mira spent by counting the dots above each tick mark and multiplying them by the corresponding time interval. Let's break it down step by step:
The tick marks on the plot are at 7, 7.5, 8, 8.5, 9, 9.5, and 10 minutes per problem.
There are 2 dots above the unlabeled tick mark between 8 and 8.5 minutes per problem. We can assume it represents 8.25 minutes.
There are 3 dots above the 9.5 minutes per problem tick mark.
Now, let's calculate the total time Mira spent:
(7 * 2) + (7.5 * 2) + (8 * 2) + (8.25 * 2) + (9 * 2) + (9.5 * 3) + (10 * 2) = 129.5 minutes.
Since Mira spent a total of 129.5 minutes on 55 problems, each problem would have taken approximately 2.36 minutes (rounded to two decimal places) if she had spent an equal amount of time on each problem.
for more such questions on amount
https://brainly.com/question/843074
#SPJ8
let's see who can solve this. pleseeee

Answers
The correlation coefficient between X and Y is Corr(X, Y) = 0.
To calculate the marginal distribution of X and Y, we need to integrate the joint probability density function (PDF) over the appropriate ranges.
a. Marginal distribution of X:
To find the marginal distribution of X, we integrate the joint PDF over the range of Y:
∫[0, 1] J(x, y) dy
Since the joint PDF is defined as J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1 and J(x, y) = 0 otherwise, the integral becomes:
∫[0, x] 1 dy = x, for 0 ≤ x ≤ 1
So, the marginal distribution of X is simply X(x) = x for 0 ≤ x ≤ 1.
b. Expectation of X:
The expectation (mean) of X can be calculated as the integral of x times the marginal PDF of X:
\(E(X) = ∫[0, 1] x * X(x) dx = ∫[0, 1] x^2 dx = [x^3/3] from 0 to 1 = 1/3\)
Therefore, the expectation of X is E(X) = 1/3.
c. Variance of X:
The variance of X can be calculated using the formula:
\(Var(X) = E(X^2) - (E(X))^2E(X^2) = ∫[0, 1] x^2 * X(x) dx = ∫[0, 1] x^3 dx = [x^4/4] from 0 to 1 = 1/4Var(X) = 1/4 - (1/3)^2 = 1/4 - 1/9 = 5/36\)
Therefore, the variance of X is Var(X) = 5/36.
d. Covariance of X and Y:
The covariance of X and Y can be calculated as:
Cov(X, Y) = E(XY) - E(X)E(Y)
Since the joint PDF J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1, the integral becomes:
\(E(XY) = ∫[0, 1] ∫[0, x] xy dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
\(E(X) = 1/3 (from part b)E(Y) = ∫[0, 1] ∫[0, x] y J(x, y) dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
Cov(X, Y) = 1/6 - (1/3)(1/6) = 0
Therefore, the covariance of X and Y is Cov(X, Y) = 0.
e. Correlation coefficient between X and Y:
The correlation coefficient can be calculated using the formula:
Corr(X, Y) = Cov(X, Y) / √(Var(X) * Var(Y))
Since the covariance of X and Y is 0, the correlation coefficient will also be 0.
Therefore, the correlation coefficient between X and Y is Corr(X, Y) = 0.
f. Conclusion based on the correlation coefficient:
The correlation coefficient of 0 indicates that there is no linear relationship between X and Y. In this case, the fraction of male runners (X) and the
for more such question on correlation visit
https://brainly.com/question/13879362
#SPJ8
David and Ken took part in a cycling race. Both of them did not change their speed throughout the race. David completed the race in 5 hours while Ken took 7 hours. Ken's average speed was 9.8 km/h less than David's average speed.
A) What was David average speed
B)What was the distance of the cycling race?
Answers
Let's assume David's average speed is S km/h.
A) To find David's average speed, we can use the formula: Speed = Distance / Time.
David completed the race in 5 hours, so his speed is S km/h. Therefore, we have:
S = Distance / 5
B) Ken's average speed is 9.8 km/h less than David's average speed, which means Ken's average speed is (S - 9.8) km/h.
Ken took 7 hours to complete the race, so we have:
S - 9.8 = Distance / 7
Now, we can solve the system of equations to find the values of S and Distance.
From equation (1): S = Distance / 5
Substitute this into equation (2):
Distance / 5 - 9.8 = Distance / 7
Multiply both sides of the equation by 35 to eliminate the denominators:
7 * Distance - 35 * 9.8 = 5 * Distance
7 * Distance - 343 = 5 * Distance
Subtract 5 * Distance from both sides:
2 * Distance - 343 = 0
Add 343 to both sides:
2 * Distance = 343
Divide both sides by 2:
Distance = 343 / 2 = 171.5 km
Therefore, the distance of the cycling race is 171.5 kilometers.
To find David's average speed, substitute the distance into equation (1):
S = Distance / 5 = 171.5 / 5 = 34.3 km/h
So, David's average speed was 34.3 km/h.\(\)
Answer:
A) 34.3 km/h
B) 171.5 km
Step-by-step explanation:
Since Ken's average speed is said to be 9.8km/h less than David's average speed, and we know that Ken's average speed is dependent on him traveling for 7 hours, then we have our equation to get the distance of the cycling race:
\(\text{Ken's Avg. Speed}=\text{David's Avg. Speed}\,-\,9.8\\\\\frac{\text{Distance}}{7}=\frac{\text{Distance}}{5}-9.8\\\\\frac{5(\text{Distance})}{7}=\text{Distance}-49\\\\5(\text{Distance})=7(\text{Distance})-343\\\\-2(\text{Distance})=-343\\\\\text{Distance}=171.5\text{ km}\)
This distance for the cycling race can now be used to determine David's average speed:
\(\text{David's Avg. Speed}=\frac{\text{Distance}}{5}=\frac{171.5}{5}=34.3\text{ km/h}\)
Therefore, David's average speed was 34.3 km/h and the distance of the cycling race was 171.5 km.
The sum of three numbers is 99. The third number is 3 times the first . The second number is 9 more than the first. What are the numbers?
Answers
Answer: This can be written as x + (x-9) + 3(x-9) = 99
5x - 36 = 99
5x = 135
x = 135/5 = 27
You can now just plug in the value of x for each of the initial terms to get:
n1 = 27
n2 = 18
n3 = 54
Step-by-step explanation:
Need help ASAP anybody got this??

Answers
Answer: uhm 6
Step-by-step explanation:
im not sure, but
1. y=9x
2. y=2x
Que son las operaciones combinadas
Answers
In mathematics, combined operations refer to the process of performing multiple mathematical operations together in a specific order.
What are the combinated operations?We understand this as the combination of mathematical operations.
The order of operations, also known as PEMDAS (Parentheses, Exponents, Multiplication and Division from left to right, Addition and Subtraction from left to right), determines the sequence in which these operations should be performed. This order ensures that calculations are carried out consistently and accurately.
For example, consider the expression "2 + 3 × 4." To solve this using combined operations, we follow the order of operations. First, we perform the multiplication: 3 × 4 = 12. Then, we perform the addition: 2 + 12 = 14. Thus, the result of this expression is 14.
LEarn more about mathematical operations:
https://brainly.com/question/4721701
#SPJ1
How do you use observed data to predict unobserved

Answers
7x2x2x2 is the prime factorization for which of the following
А
72
B
56
С
44
D
28
Answers
Will someone be able to help me with this math problem, the picture is down below. Please help

Answers
The dilation transformation of the triangle ABC by a scale factor of 3, with the point P as the center of dilation indicates;
Side A'B' will be parallel to side AB
Side A'C' will be parallel to side AC
Side BC will lie on the same line as side BC
What is a dilation transformation?A dilation transformation is one in which the dimensions of a geometric figure are changed but the shape of the figure is preserved.
The possible options, from a similar question on the internet are;
Be parallel to
Be perpendicular to
Lie on the same line as
The location of the point P, which is the center of dilation, and the lines PC and PA of dilation and the scale factor of dilation indicates that we get;
PB' = 3 × PB
PA' = 3 × PA
PC' = 3 × PC
Therefore; The side B'C' will be on the same line as the side BC
The Thales theorem, also known as the triangle proportionality theorem indicates that;
The side A'C' will be parallel to the side AC
The side A'B', will be parallel to the side AB
Learn more on the Thales theorem here: https://brainly.com/question/14417137
#SPJ1
The first sequence rule is multiply by 3 starting from 5. The second sequence rule is add 9 starting from 18. What is the first number that appears in both sequences?
27
45
72
135
what is the answer
Answers
Considering the sequences given, the first number that appears in both sequences is given by: 45.
What numbers appear in the first sequence?The rule is multiply by 3 starting from 5, hence the numbers are:
(5, 15, 45, 135, ...).
What numbers appear in the second sequence?The rule is add 9 starting from 18, hence the numbers are:
(18, 27, 36, 45, ...).
45 is the first number that appeared in both sequences.
More can be learned about sequences at https://brainly.com/question/6561461
#SPJ1
When rounding to the nearest 100, what are the greatest and least numbers that can be rounded to 500?
Answers
The most used rule to rounding a number to the nearest hundred is the following:
• If the last two digits in the number are ,50 or above,, we round ,up,;
,• if the last two digits are ,49 or below,, we round ,down,.
Then, all the numbers from 450 to 549 can be rounded to 500.
Therefore, the greatest is 549 and the least is 450.
Mary is planning to survey a sample of women to find out how much money the average woman spent on lipstick last year. What sample size will she need, if she wants to be 95% confident that her sample mean is no more than $4 away from the population mean, and assuming a standard deviation of $20? A. 100
Answers
Answer: The required sample size = 97
Step-by-step explanation:
If prior population standard deviation is known, then the minimum sample size can be computed as:
\(n=(\frac{z^*\times\sigma}{E})^2\)
,where z* = critical z-value
\(\sigma\) = population standard deviation
E = Margin of error
As per given,
\(\sigma=20,\ E= 4\)
Critical value for 95% confidence = 1.96
\(n=(\frac{1.96\times20}{4})^2\\= (1.96\times 5)^2\\= (9.8)^2\\=96.04\approx97\)
Hence, the required sample size = 97
The coordinates of the vertices of a polygon are shown on the graph below.
What is the name of the polygon?
octagon
pentagon
quadrilateral
triangle

Answers
Answer:
Triangle
Step-by-step explanation:
It has three side unlike the others can't have three sides