Find the value of the y when 5y + 45 = 100
Answers
Related Questions
During WW! mortars were fired from trenches 3 feet down The mortars had a velocity of 150 ft/s. Determine how long it will take for the mortar shell to strike its target?
Answers
The mortar shell will strike the target in 0.02 seconds
How to find the durationThe duration to strike the target is solved using the formula for velocity which is
= distance / time
The problem gives the distance to be 3 feet and velocity is 150ft/s
therefore
150 = 3 / time
time = 3 / 150
time = 0.02 seconds
Learn more on velocity at:
https://brainly.com/question/25749514
#SPJ1
Engineers must consider the diameters of heads when designing helmets. The company researchers have determined that the population of potential clientele have head diameters that are normally distributed with a mean of 5.8-in and a standard deviation of 0.8-in. Due to financial constraints, the helmets will be designed to fit all men except those with head diameters that are in the smallest 4.1% or largest 4.1%.
1. What is the minimum head breadth that will fit the clientele?
2. What is the maximum head breadth that will fit the clientele?
Answers
Answer:
1. The minimum head breadth that will fit the clientele is of 4.41-in.
2. The maximum head breadth that will fit the clientele is of 7.19-in.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Normally distributed with a mean of 5.8-in and a standard deviation of 0.8-in.
This means that \(\mu = 5.8, \sigma = 0.8\)
1. What is the minimum head breadth that will fit the clientele?
The 4.1st percentile, that is, X when Z has a pvalue of 0.041, so X when Z = -1.74.
\(Z = \frac{X - \mu}{\sigma}\)
\(-1.74 = \frac{X - 5.8}{0.8}\)
\(X - 5.8 = -1.74*0.8\)
\(X = 4.41\)
The minimum head breadth that will fit the clientele is of 4.41-in.
2. What is the maximum head breadth that will fit the clientele?
100 - 4.1 = 95.9th percentile, that is, X when Z has a pvalue of 0.959, so X when Z = 1.74.
\(Z = \frac{X - \mu}{\sigma}\)
\(1.74 = \frac{X - 5.8}{0.8}\)
\(X - 5.8 = 1.74*0.8\)
\(X = 7.19\)
The maximum head breadth that will fit the clientele is of 7.19-in.
What is the quotient? URGENT!!

Answers
Answer:
The answer is A.
Step-by-step explanation:
You have to multiply by converting the second fraction into upside down :
\( \frac{4x + 1}{6x} \div \frac{x}{3x - 1} \)
\( = \frac{4x + 1}{6x} \times \frac{3x - 1}{x} \)
\( = \frac{(4x + 1)(3x - 1)}{x(6x)} \)
\( = \frac{12 {x}^{2} - 4x + 3x - 1}{6 {x}^{2} } \)
\( = \frac{12 {x}^{2} - x - 1 }{6 {x}^{2} } \)
which inequality describes the possible values of x? there are three triangles , triangle abc, triangle cde, and triangle efg. the points a, c , e, and g are collinear, points b, c, and d are collinear, and points d, e, and f are collinear. side ac, side ce, and side eg are congruent to each other. side ab, side de, and side ef are congruent to each other. the length of side bc is 12 and the length of side cd is 10. the measure of angle bac is 50 degrees and the measure of angle dec is (5x-10) degrees. a. 2 < x < 5 b. 2 < x < 10 c. 2 < x < 12 d. 2 < x < 22
Answers
The inequality that describes the possible value of x is
c. 2 < x < 12How to find the value of xThe triangles described gave the information to form the inequality equation
from the description it can be deduced that
m< bca = m< dce vertical angles
since side 12 is greater than 10 then m< bac > m< dec
therefore 50 > 5x - 10
solving for x
50 > 5x - 10
50 + 10 > 5x
60 > 5x
x < 12
therefore 2 < x < 12 is the inequality that represents x
Learn more about inequality at:
https://brainly.com/question/29244324
#SPJ1
given the function f(x)=logbase2(X), find the y-intercept of g(x) = f(x+4)+8
Answers
The y-intercept of f(x + 4) + 8 is given as follows:
10.
What is a translation?A translation happens when either a figure or a function is moved horizontally or vertically on the coordinate plane.
The four translation rules for functions are defined as follows:
Translation left a units: f(x + a).Translation right a units: f(x - a).Translation up a units: f(x) + a.Translation down a units: f(x) - a.The parent function for this problem is given as follows:
\(f(x) = \log_2{x}\)
The translated function is then given as follows:
\(g(x) = \log_2{x + 4} + 8\)
The y-intercept of the function is the numeric value at x = 0, hence:
\(g(0) = \log_2{0 + 4} + 8\)
g(0) = 2 + 8 = 10.
More can be learned about translations at brainly.com/question/28174785
#SPJ1
Please help I need this will give 100 points please help

Answers
The solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Solving Inequality in a given domainGiven the inequality,
f(x²-2) < f(7x-8) over D₁ = (-∞, 2)
We need to find the values of x that satisfy this inequality.
Since we know that f is increasing over its domain, we can compare the values inside the function to determine the values of x that satisfy the inequality.
First, we can find the values of x that make the expressions inside the function equal:
x² - 2 = 7x - 8
Simplifying, we get:
x² - 7x + 6 = 0
Factoring, we get:
(x - 6)(x - 1) = 0
So the values of x that make the expressions inside the function equal are x = 6 and x = 1.
We can use these values to divide the domain (-∞, 2) into three intervals:
-∞ < x < 1, 1 < x < 6, and 6 < x < 2.
We can choose a test point in each interval and evaluate
f(x² - 2) and f(7x - 8) at that point. If f(x² - 2) < f(7x - 8) for that test point, then the inequality holds for that interval. Otherwise, it does not.
Let's choose -1, 3, and 7 as our test points.
When x = -1, we have:
f((-1)² - 2) = f(-1) < f(7(-1) - 8) = f(-15)
Since f is increasing, we know that f(-1) < f(-15), so the inequality holds for -∞ < x < 1.
When x = 3, we have:
f((3)² - 2) = f(7) < f(7(3) - 8) = f(13)
Since f is increasing, we know that f(7) < f(13), so the inequality holds for 1 < x < 6.
When x = 7, we have:
f((7)² - 2) = f(47) < f(7(7) - 8) = f(41)
Since f is increasing, we know that f(47) < f(41), so the inequality holds for 6 < x < 2.
Therefore, the solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Learn more about inequality here:
https://brainly.com/question/25944814
#SPJ1
Q2) The number of people signed up for a bus trip increased from 32 to
45. What is the percent increase?
Answers
Answer:
45-32 = 13 / 32 *100= 40.625 round to the nearest percent is 41%
Step-by-step explanation: Brainlest plzzz
Please help ASAP! Thank you

Answers
Answer:
a. lines intersecting at a single point
b. one solution
Step-by-step explanation:
a. The equations can be rewritten as:
y = -5x+23 and y = -1/6x+1
Comparing the equations with standard equation: y=mx+c, where m is the gradient of the line formed by the linear equation.
Since the gradient of the lines are different then the lines cannot be parallel and will intersent at one point.
b. The equation will have one solution as below.
The equations can be rewritten as:
5x+y=23
5x+30y=30
Subtracting both equation will result in,
29y=7
=> y=7/29
Hence x= 660/29
Suppose f(x) is a function which satisfies f'(3) = 0,f'(5) = 0, f"(3) = -4, and f"(5) = 5.
Which of the following statements is true?
A. f(x) has a relative minimum at x = 3 and at x = 5.
B. f(x) has a relative minimum at x = 3 and a relative maximum at x = 5.
C. f(x) has a relative maximum at x = 3 and at x = 5.
D. f(x) has a relative maximum at x = 3 and a relative minimum at x = 5.
E. None of the above is true,
Any help
Answers
Using the concept of critical point and the second derivative test, it is found that the correct option is:
D. f(x) has a relative maximum at x = 3 and a relative minimum at x = 5.
The critical points of a function \(f(x)\) are the values of x for which \(f^{\prime}(x) = 0\).Applying the second derivative test at the critical points, we have that:
If positive, that is, \(f^{\prime\prime}(x) > 0\), it is a relative minimum.If negative, that is, \(f^{\prime\prime}(x) < 0\), it is a relative maximum.If zero, that is, \(f^{\prime\prime}(x) = 0\), we do not have sufficient information.In this problem:
\(f^{\prime}(3) = 0, f^{\prime\prime}(3) < 0\), thus, there is a maximum at x = 3.\(f^{\prime}(5) = 0, f^{\prime\prime}(5) > 0\), thus, there is a minimum at x = 5.The correct option is:
D. f(x) has a relative maximum at x = 3 and a relative minimum at x = 5.
A similar problem is given at https://brainly.com/question/16944025
Please answer quick! I have a headache and I don't want to do the work.. Giving brainliest to the RIGHT ANSWER.
How many 1/8's are in 25?
Answers
Answer:
There are 200 1/8's in 25.
Step-by-step explanation:
If I am thinking of this correctly then there are 200. Basically, what how I interpreted this is that you mean 8 1/8's make up 1. and you need 25 whole 1's. If that is the case the correct answer is 200.
200 1/8. Hope this helps and feel better!
a certain ceiling is made up of tiles.every square mater of ceiling requries 10.75 tiles.fill in table with the missing values
Answers
Table is attached below-
1) 1 m² = 10.75 tiles
2) 10 m² = 107.5 tiles
3) 9.3 m² of tiles = 100 tiles
4) a m² = 10.5a tiles
We have been given that
Every square meter of ceiling requires 10.75 tiles.
we have find missing values in the table.
We know,
1 square meter of ceiling = 10.75 tiles. ...(i)
1. Therefore, the number of tiles corresponding to 1 square meter of ceiling is 10.75.
Multiply both sides by 10.
10×1 square meter of ceiling = 10×10.75 tiles.
10 square meter of ceiling = 107.5 tiles.
2. Therefore, the number of tiles corresponding to 10 square meter of ceiling is 107.5.
Divide both sides by 10.75 in (i).
(1/10.75) square meter of ceiling = 1 tile.
Multiply both sides by 100.
(100/10.75) square meter of ceiling = 100 tiles.
On approximating the value, we get
9.3 square meter of ceiling = 100 tiles.
3. Therefore, the square meters of ceiling corresponding to 100 tiles is about 9.3.
Multiply both sides by a in (i).
a×1 square meter of ceiling = a×10.75 tiles.
a square meter of ceiling = 10.75a tiles.
4. Therefore, the number of tiles corresponding to a square meter of ceiling is 10.75a.
To learn more about Missing Values
visit : brainly.com/question/23157965
#SPJ9


What is the solution of the equation 3/4x + 5 = -9
PLEASE HELPPPP

Answers
Answer:
-18 2/3 or -56/3
Step-by-step explanation:
The right rectangular prisms are similar. which statements are correct? check all that apply. the angles in the smaller prism measure 90 degrees. the perimeter of the rectangular bases changes by a factor of 2. the surface area changes by a factor of 8. the larger prism has twice the volume of the smaller prism. the area of the rectangular bases changes by a factor of 4.
Answers
The true statement about the right rectangular prisms include:
The angles in the smaller prism measure 90 degrees. The perimeter of the rectangular bases changes by a factor of 2.The rectangular bases changes by a factor of 4.How to illustrate the prism?It should be noted that a prism simply means a shape that has two identical shapes that face each other.
Here, the angles in the smaller prism measure 90 degrees and the perimeter of the rectangular bases changes by a factor of 2.
Learn more about prism on:
https://brainly.com/question/23963432
#SPJ4
Answer:
1,2, and 5
Step-by-step explanation:
\(\frac{7}{12} + \frac{2}{3} =\)
Answers
. Find all possible solutions for x. Be careful of domain restrictions.
log_2(x^2-4) - log_2(x+2) = 2log_2(x-4)
Answers
Answer:
x=6
Step-by-step explanation:
all the details are in the attached picture. The suggested solution is not the shortest way.
Note, step 1 is: to find the domain; step 2 is: to solve the equation wihout domain; step 3: to determine 'x' with domain. The answer is marked with green colour.

1 2 3 4 5 6 7 8 9 10
TIME REMAINING
57:04
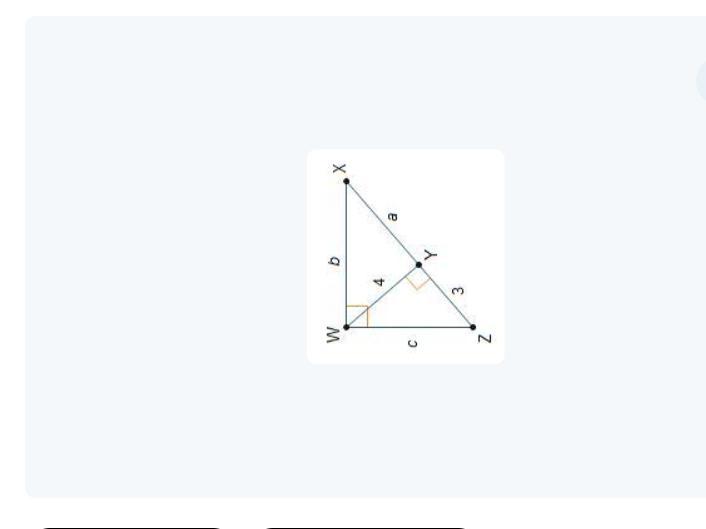
Triangle X Y Z is shown. Angle Z W X is a right angle. An altitude is drawn from point W to point Y on side Z X to form a right angle. The length of W Y is 4, the length of Y X is a, the length of Z Y is 3, the length of Z W is c, and the length of W X is b.
What is the value of a?
5 units
5 and one-third units
6 and two-thirds units
7 units
Answers
Option B. 5 and one-third units. The value of a in triangle XYZ is 5 and two-thirds units. This is found using the Pythagorean theorem twice and solving for a.
To find the value of a, we can use the Pythagorean theorem in triangles WZY and WYX as follows:
In triangle WZY:
\(c^2 = 3^2 + (a + 4)^2\)
In triangle WYX:
\(b^2 = 4^2 + a^2\)
Since angle ZWX is a right angle, we can use the Pythagorean theorem in triangle ZWX as follows:
\(ZWX^2 = ZW^2 + WX^2\)
We know that ZW = c and WX = b, so we have:
\(a^2 + b^2 = c^2\)
Substituting\(c^2\) in terms of a and simplifying, we get:
\(a^2 + b^2 = 25 + (a + 4)^2\)
Expanding and simplifying, we get:
\(a^2 + b^2 = a^2 + 8a + 41\)
Subtracting \(a^2\) from both sides, we get:
\(b^2 = 8a + 41\)
Substituting \(b^2\) in terms of a in the equation \(a^2 + b^2 = c^2\), we get:
\(a^2 + 8a + 41 = c^2\)
Substituting\(c^2\) in terms of a from the equation for triangle WZY, we get:
\(a^2 + 8a + 41 = 9 + (a + 4)^2/16\)
Expanding and simplifying, we get:
\(16a^2 + 128a + 656 = 9a^2 + 50a + 97\)
Simplifying further, we get:
\(7a^2 + 78a - 559 = 0\)
Using the quadratic formula, we get:
\(a = (-78 ± sqrt(78^2 + 4(7)(559))) / 14\)
a = (-78 ± sqrt(49379)) / 14
Since a represents a length in a triangle, it must be positive. Therefore, we have:
a = (sqrt(49379) - 78) / 14 ≈ 6.67
To learn more about Pythagorean theorem please click on below link.
https://brainly.com/question/14930619
#SPJ1
Triangle X Y Z is shown. Angle Z W X is a right angle. An altitude is drawn from point W to point Y on side Z X to form a right angle. The length of W Y is 4, the length of Y X is a, the length of Z Y is 3, the length of Z W is c, and the length of W X is b.
What is the value of a?
A. 5 units
B. 5 and one-third units
C. 6 and two-thirds units
D. 7 units
Work out the size of AED. Work out x

Answers
Answer:
a). m∠AED = 70°
b). x = 10°
Step-by-step explanation:
a). Quadrilateral ABDE is a cyclic quadrilateral.
Therefore, by the theorem of cyclic quadrilateral,
Sum of either pair of opposite angle is 180°
m(∠AED) + m(∠ABD) = 180°
m(∠AED) = 180° - 110°
m(∠AED) = 70°
Since, ∠AED ≅ ∠EAD
Therefore, m∠AED = m∠EAD = 70°
b). By triangle sum theorem in ΔABD,
m∠ABD + m∠BDA + m∠DAB = 180°
110° + 40° + m∠DAB = 180°
m∠DAB = 180° - 150°
m∠DAB = 30°
m∠BAE = m∠EAD + m∠BAD
= 70° + 30° = 100°
By angle sum theorem in ΔACE,
m∠EAC + m∠AEC + m∠ACE = 180°
100° + 70° + x° = 180°
x = 180° - 170°
x = 10°
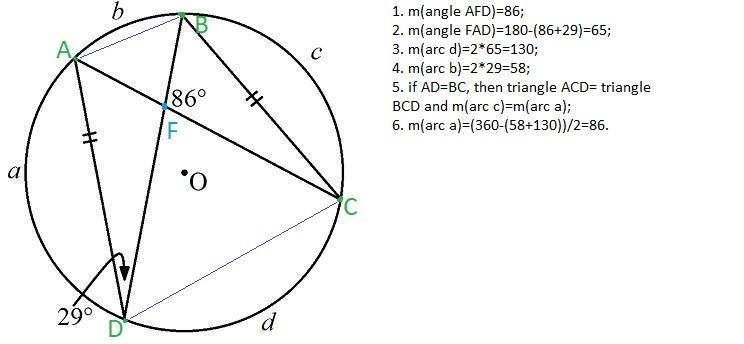
Find the value of a.

Answers
Answer:
86°
Step-by-step explanation:
try suggested solution (see the attached picture), note, the suggested way is not the shourtest one.
I need help please i will give brainliest

Answers
Answer:
5 packages
Step-by-step explanation:
each would have five if they made 5 sandwhiches
Answer:
5
Step-by-step explanation:
Divide each number until the remainder is one
Multiply the numbers used to divide which is 2 6 and 5 to get the LCM which is 60
Edit:
60 eggs /12 =5
60 muffins/10 =5

Linear sequence of 35/100,5/10,65/100
Answers
The linear rule for the sequence is f(n) = 7/20 + 3/20(n - 1)
Finding the linear rule for the sequenceFrom the question, we have the following parameters that can be used in our computation:
35/100,5/10,65/100
In the above sequence, we can see that 15/100 is added to the previous term to get the new term
This means that
First term, a = 35/100
Common difference, d = 15/100
The nth term is then represented as
f(n) = a + (n - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(n) = 35/100 + 15/100(n - 1)
So, we have
f(n) = 7/20 + 3/20(n - 1)
Hence, the explicit rule is f(n) = 7/20 + 3/20(n - 1)
Read more about sequence at
brainly.com/question/30499691
#SPJ1
The diameter
of the Earth is 1.3 × 10 km.
The diameter of the Moon is 3.5 × 10 km.
The diameter of the Sun is 400 times greater
than the diameter of the Moon.
How many times smaller is the diameter of
the Earth than the diameter of the Sun
Answers
Earth's diameter is 0.0092 times less than the sun's diameter.
Ratio, in math, is a time period this is used to examine or greater numbers. It is used to indicate how large or small a sum is in comparison to another.In a ratio, portions are as compared the use of division. Here the dividend is referred to as the `antecedent' and the divisor is referred to as the 'consequent'. For example, in a collection of 30 people, 17 of them opt for to stroll within side the morning and thirteen of them favor to cycle. We use the ratio formulation whilst evaluating the connection among numbers or portions. The popular shape of representing a ratio of among portions say 'a' and 'b' is a: b, that's examine as 'a is to b'.The Diameter of Earth = 1.3 * 10⁴ km
The Diameter of Moon = 3.5 * 10³ km
Let the diameter of sun be x km
According to the question
The diameter of the sun is 400 times that of the moon.
x = 400 * 3.5 * 10³ km
= 14 * 10⁵ km
The Diameter of earth / diameter of sun
= 1.3 * 10⁴ / 14 * 10⁵
= 0.0092
Hence, The diameter of the Earth is 0.0092 times that of the Sun.
Learn more about diameter here
https://brainly.com/question/13614093
#SPJ9
When a grizzly bear hibernates, its heart rate drops 10 beats per minute, which is 20% of its normal value. What is the grizzly bear's normal heart rate when it is not hibernating?
Answers
Answer:
50
Step-by-step explanation:
Let's call the grizzly bear's normal heart rate x.
According to the problem, when the grizzly bear hibernates, its heart rate drops 10 beats per minute, which is 20% of its normal value. In other words, the amount that the heart rate drops is 20% of the normal heart rate.
We can set up an equation to represent this:
20% of x = 10
To solve for x, we can start by simplifying the left side of the equation. We can convert the percentage to a decimal by dividing by 100:
0.2x = 10
Then, we can isolate x by dividing both sides by 0.2:
x = 50
Therefore, the grizzly bear's normal heart rate when it is not hibernating is 50 beats per minute.
Answer:
50 bpm
Step-by-step explanation:
20% of a value is also 1/5 of a value.
Since the 10 bpm is 1/5 the normal value of the bear's heart rate, we just need to multiply 10 by 5 to get the normal heart rate:
10*5 = 50
Meaning that the bear's normal heart rate is 50 bpm.
Jude is making a door for a door frame with an opening that measures 9 feet by 3 feet. Which diagonal length should
he use to make a door that fits in the door frame?
10 feet
90feet (squared)
72 feet (squared)
12 feet
Answers
The diagonal length should he use to make a door that fits in the door frame is √90 feet, Option 'B' is the correct answer.
Pythagorean theorem based problem:What information do we have?
Length of door = 9 feet
Width of door = 3 feet
Using Pythagorean theorem,
H = √B² + P²
H = √3² + 9²
H = √9 + 81
H = √90 feet
Find out more information about 'Pythagorean'.
https://brainly.com/question/15190643?referrer=searchResults
Find the midpoint of each line segment.

Answers
Answer:
(1.5, 0.5)
Step-by-step explanation:
(5, 3) and (-2, -2)
5 - 2 / 2 = 1.5
-2 + 3 / 2 = 0.5
What is a reasonable estimate for the limit of hhh at x=3x=3x, equals, 3?
Answers
Answer:
Limit does not exist.
Step-by-step explanation:
From the graph, notice that the limit does not exist, when you move to the right the limit tend to -3 and when you approach from the left your limit approaches 4, therefore since the right and left limit are not equal the limit does not exist.

HELP I WILL GIVE BRAINLIEST IF RIGHT

Answers
Answer:
a
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
I might be wrong but i'm pretty sure it's right
Select the correct answer.
A home-based sign company uses this function to model its monthly profit, where x is the price of each sign it sells.
p(x) = -10x^2 + 498x - 1,500
what is the company's profit if it sells each sign for $20?
A. $18,020
B. $4,460
C. $14,420
D. $1,402
Answers
The profit made id each sign is sold for $20 is $4460
The profit model, P(x) = -10x² + 498x - 1,500
Where, x = price per sign sold
If the price per sign sold is $20. Hence, x = $20
The profit made can be calculated thus :
Put x = 20 in the profit function :
P(20) = -10(20)² + 498(20) - 1,500
P(20) = - 10(400) + 9960 - 1500
P(20) = - 4000 + 9960 - 1500
P(20) = $4,460
The profit made is $4,460
Learn more : https://brainly.com/question/18109354
Answer:
$4,460
Step-by-step explanation:
I got a 100% on my test
which of the following is equivalent to x^2 -5x +6
Answers
Hello!
x² - 5x + 6
= (x² - 2x) + (-3x + 6)
= x(x - 2) - 3(x - 2)
= (x - 2)(x - 3)
If f(x) = 10 - 3x, what is the value of f(2)?
Answers
Answer:
4
Step-by-step explanation:
Put 2 where x is and do the arithmetic.
f(2) = 10 -3∙2 = 10 -6
f(2) = 4
15. Which one of the following is a geometric sequence?
O A. 0, 1, 2, 3,...
O B. 2, -3, 92, -18/4
O C. -7, 10, 23, 36, ...
O D. 8, 4, 2, 1, 1/2, ¹/4....