Find the value of the permutation.
P(5,0)
P(5,0)= (Simplify your answer.)
www
Answers
The value of the permutation P(5,0) is 1.
To find the value of the permutation P(5,0), we can use the formula:
P(n, r) = n! / (n - r)!
In this case, we have n = 5 and r = 0.
Substituting these values into the formula, we get:
P(5,0) = 5! / (5 - 0)!
Since any number factorial is equal to 1, we have:
P(5,0) = 5! / 5!
Simplifying further:
P(5,0) = 1
Therefore, the value of the permutation P(5,0) is 1.
Learn more about Permutation here:
https://brainly.com/question/29990226
#SPJ1
Related Questions
The shapes below are drawn on a centimetre grid. Show that the triangle and the square have the same area.

Answers
Both figures have an area of 4 units squared, so yea, the area is the same.
How to find the areas?The area of a square of side length S is equal to S squared, for the square, we can see that:
S = 2 units.
Then the area is:
A = (2 units)² = 4 square units.
For the triangle, we know that the area is equal to:
A = B*H/2
Where B = base, H = height.
We can see that:
B = 2 units.
H = 4 units.
Then:
A = (2 units)*(4 units)/2= 4 square units.
So yea, both have the same area.
Learn more about area at:
https://brainly.com/question/24487155
#SPJ1
Find the Quadratice function \(y=a(x-h)x^{2}\) with given vertex (5,8) and given point (1,3)
Answers
Given:
Consider the quadratic function is
\(y=a(x-h)^2+k\)
With given vertex (5,8) and given point (1,3).
To find:
The equation of quadratic function.
Solution:
The quadratic function is
\(y=a(x-h)^2+k\) ...(i)
Where, (h,k) is the vertex and a is a constant.
Vertex is (5,8). So,
\((5,8)=(h,k)\)
\(h=5,k=8\)
Putting \(h=5,k=8\) in (i), we get
\(y=a(x-5)^2+8\) ...(ii)
The given point is (1,3). Putting x=1 and y=3 in (ii), we get
\(3=a(1-5)^2+8\)
\(3-8=a(-4)^2\)
\(-5=16a\)
\(-\dfrac{5}{16}=a\)
Putting \(a=-\dfrac{5}{16}\) in (ii), we get
\(y=-\dfrac{5}{16}(x-5)^2+8\)
Therefore, the required quadratic function is \(y=-\dfrac{5}{16}(x-5)^2+8\).
Question Multiply. (−1115)⋅(−35) What is the product? Enter your answer as a simplified fraction in the box.
Answers
The product of -1115 and - 35 is 39025
How to solve multiplication problem?We have to find the product of -1115 and - 35.
This simply means we have to multiply -1115 by -35.
Recall the product of negative and negative is positive.
Hence,
- 1115 × - 35 = (- × -) (1115 × 35)
- 1115 × - 35 = 39025
Therefore, the product of -1115 and - 35 is 39025
learn more on multiplication here: https://brainly.com/question/3023273
#SPJ1
Answer: its 11/25. I did the test trust me-
Use the spinner to find the theoretical probability of the event. Write your answer as a fraction or a percent rounded to the nearest tenth.
Answers
The theoretical probability of spinning red is given as follows:
1/3.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
For the spinner in this problem, 2 out of 6 regions are red, hence the theoretical probability is given as follows:
2/6 = 1/3.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

Out of a total of 10 college textbooks estimate the standard deviation of their ages if the oldest textbook is known to be 7.9 years old and the newest textbook is 1.3 years old.
A. 0.5 years
B. 1.1 years
C. 2.3 years
D. 2.9 years
E. 3.3 years
Answers
Answer: The answer is D 2.9 years
Step-by-step explanation:
find the exact value using formulas from geometry. ∫ (1+3x) with upper bound as 3 and lower bound as 1.
Answers
The value of the integral ∫(1+3x) dx is equal to 14.
What is integration?Integration is a process of adding up small elemental volumes to find the larger volume.
Given is to find the integral -
∫(1+3x)
We can find the equivalent values as -
∫(1+3x) dx = ∫1 dx + ∫3x dx
∫(1+3x) dx = x + 3x²/2
For the limit x = 1 to x = 3, we can write -
∫(1+3x) dx = (3 + 27/2) - (1 + 3/2)
∫(1+3x) dx = 33/2 - 5/2 = 14
Therefore, the value of the integral ∫(1+3x) dx is equal to 14.
To solve more questions on integrals, visit the link -
brainly.com/question/30098550
#SPJ1
Does the graph represent a function? Why or why not ?

Answers
Answer:
A.
Step-by-step explanation:
The vertical line test is a way of finding out if a relation is a function.
Graph the relation.
Then imagine a vertical line moving from left to right over the graph of the relation.
If the vertical line intersects at most one point of the graph in any position you place the vertical line, then the relation is a function.
This function passes the vertical test since it never intersects more than one point on the vertical line at a time.
Answer: A.
cuanto es 1 mas 1? dende ecuaciones y detalles es para mi examen virtual please
Answers
Answer:
2
Step-by-step explanation:
1+1=2
A contractor better job at $750 for materials plus $43 per hour for labor. The total cost for the job can be modeled by C= 43H+ 750$.
Find the number of hours that he has for the job if the owner would like the total cost to be under $2000, rounded to the nearest hour.
Answers
The contractor has a maximum of 29 hours (rounded down) to complete the job while keeping the total cost under $2000.
To find the number of hours the contractor has for the job while keeping the total cost under $2000, we can use the given cost model equation: C = 43H + 750.
Since the owner wants the total cost to be under $2000, we can set up the inequality:
43H + 750 < 2000
Now, let's solve this inequality for H, the number of hours:
43H < 2000 - 750
43H < 1250
Dividing both sides of the inequality by 43:
H < 1250/43
To determine the maximum number of hours the contractor has for the job, we need to round down the result to the nearest whole number since the contractor cannot work a fraction of an hour.
Using a calculator, we find that 1250 divided by 43 is approximately 29.07. Rounding down to the nearest whole number, we get:
H < 29
Using the cost model equation C = 43H + 750, where C represents the total cost and H represents the number of hours, we set up the inequality 43H + 750 < 2000 to satisfy the owner's requirement of a total cost under $2000.
By solving the inequality and rounding down to the nearest whole number, we find that the contractor has a maximum of 29 hours to complete the job within the specified cost limit.
For more such question on cost. visit :
https://brainly.com/question/2292799
#SPJ8
Please help. Plotting mixed numbers on a number line is really confusing for me.

Answers
Answer:
Go to the whole number of the mixed number then find that whole number on the line plot. Then skip 4 out of 5 jumps. For example, skip 4 jumps then you will get the fraction 4/5. So now we move onto 2 7/10. (2.7 as a decimal) Go to the whole number 2 on the line plot. Then jump 7 times in. Each jump should represent 1/10 or 0.1. So now you found the line plots of 1 4/5 and 2 1/10.
Step-by-step explanation:
I explained everything above. :)
Please mark brainliest.
In a class of students, the following data
table summarizes how many students have a
cat or a dog. What is the probability that a
student chosen randomly from the class has
a cat?
Has a dog
Does not have a
dog
Has a cat
2
3
Does not have a
cat
12
10
Answers
The table can be summarized as follows:
| | Has a dog | Does not have a dog |
|----------|-----------|---------------------|
| Has a cat | 2 | 3 |
| Does not have a cat | 12 | 10 |
To find the probability that a student chosen randomly from the class has a cat, we need to find the total number of students who have a cat (regardless of whether or not they have a dog), and divide it by the total number of students in the class.
The number of students who have a cat is 2 (those who have a dog and a cat) + 3 (those who have a cat but do not have a dog) = 5.
The total number of students in the class is the sum of all four categories: 2 (has a cat and a dog) + 3 (has a cat, does not have a dog) + 12 (does not have a cat, has a dog) + 10 (does not have a cat, does not have a dog) = 27.
So, the probability that a student chosen randomly from the class has a cat is 5/27.
The ages of the signers of the Declaration of Independence are shown. (Age is approximate since only the birth year appeared in the source, and one has been omitted since his birth year is unknown.) Construct a grouped frequency distribution and a cumulative frequency distribution for the data, using 7 classes.
Answers
Answer:
Step-by-step explanation:
The ages of the signers of the Declaration of Independence are shown. (Age is approximate since only the birth year appeared in the source, and one has been omitted since his birth year is unknown.) Construct a grouped frequency distribution and a cumulative frequency distribution for the data using 7 classes. Limits Boundaries 27-33 26.5-33.5 7 41 54 47 40 39 35 50 37 49 42 70 32 44 52 39 50 40 30 34 69 39 45 33 42 44 63 60 27 42 34 50 42 52 38 36 45 35 43 48 46 31 27 55 63 46 33 60 62 35 46 45 34 53 50 50 34-40 33.5-40.5 14 41-47 40.5-47.5 15 48-54 11 47.5-54.5 54.5-61.5 55-61 3 62-68 61.5-68.5 3 69-75 68.5-75.5 55
An office manager orders one calculator or one calendar for each of the office's 60 employees. Each calculator costs $15, and each calendar costs $10. The entire order totaled $800.
Part A: Write the system of equations that models this scenario. (5 points)
Part B: Use substitution method or elimination method to determine the number of calculators and calendars ordered. Show all necessary steps. (5 points)
Answers
The system of equations is.
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
And the solutions are y = 50 and x = 10.
How to write and solve the system of equations?Let's define the two variables:
x = number of calculators.y = number of calendars.With the given information we can write two equations, then the system will be:
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
Now let's solve it.
We can isolate x on the first to get:
\(\text{x} = 60 - \text{y}\)
Replace that in the other equation to get:
\(15\times(60 - \text{y}) + 10\text{y} = 800\)
\(-2\bold{y} = 900 - 800\)
\(-2\bold{y} = 100\)
\(\text{y} = \dfrac{100}{-2} = \bold{50}\)
Then \(\bold{x=10}\).
Therefore, the solutions are y = 50 and x = 10.
Learn more about systems of equations at:
https://brainly.com/question/31812807
let be a diagonalizable matrix. if is the solution to the system , then check all the possible values of and below. (a); (b) ; (c) ; (d) ; (e) ; (f) .
Answers
Let A be a diagonalizable matrix. If c₁ and c₂ are solution to system
x⃗' (t) = A x⃗ ( t )
the possible values of c₁ is 1 and c₂ is 2 .
So, the correct option is option(a) and (e).
We have given that A is 2 × 2 diagonalizable matrix and x⃗ (t) = ( 3eᵗ + eᶜ₁t , 3e²ᵗ + eᶜ₂ᵗ) is a solution of system, x⃗ '(t) = A x⃗(ᵗ) .
A Solution of system always satisfied the equation of system.
Now, Differenating x⃗ (t) wih respect to t we get, x⃗' (t)=( 3eᵗ + c₁ eᶜ₁t , 6e²ᵗ + c₂ eᶜ₂ᵗ)
So, ( 3eᵗ + c₁ eᶜ₁t , 6e²ᵗ + c₂ eᶜ₂ᵗ)= A ( 3eᵗ + eᶜ₁t , 3e²ᵗ + eᶜ₂ᵗ) where A is diagonalizable and A = [a 0 0 b].
Then, ( 3eᵗ + c₁ eᶜ₁t , 6e²ᵗ + c₂ eᶜ₂ᵗ) = ( 3aeᵗ + aeᶜ₁t , 3be²ᵗ + b eᶜ₂ᵗ)
equating the coefficients on both sides we get, 3eᵗ + c₁ eᶜ₁t = 3aeᵗ + aeᶜ₁t 6e²ᵗ + c₂ eᶜ₂ᵗ = 3be²ᵗ + b eᶜ₂ᵗ
after equating the corresponding equations , 3 = 3a and c₁ = a and 6 = 3b and c₂ = b after solving all we get a = 1 and b = 2 which implies c₁ = 1 and c₂ = 2. Hence, the possible values are c₁ = 1 and c₂ = 2.
To learn more Diagonalizable matrix, refer :
https://brainly.com/question/29583376
#SPJ4
Complete question:
Let A be a diagonalizable matrix. If c₁ and c₂ are solution to system x⃗ (t) = A x⃗
then check all the possible values of c₁ and c₂ and below.
(a) c₁ = 1
(b) c₁ = 3
(c) c₁ = 2
d) c₂ = 1
(e)c₂ =2
(f) c₂ = 3
(I WILL GIVE BRAINLIEST) PLEASE HELP!!

Answers
Answer:
C. I,II,III
Step-by-step explanation:
Absolute value is the distance of a number from 0 on a number line. 6 is 6 units from 0, therefore this option is correct. -6 is 5 units to the left of 0, but it is still 6 units away, therefore this option is correct. 6 is 6 units away from 0, therefore, III is correct. But 0 is 0 units away from 0, therefore this option is incorrect.
Algebra transformation
f(x) =
f(x) =
f(x) =
f(x) =

Answers
Algebra transformation
for Graph1 f(x)=f(x)+4
for Graph2 f(x)=-f(x-4)
for Graph3 f(x)=f(x-7)
for Graph4 f(x)=f(x-2)-5
Define reflection of graphIn mathematics, the reflection of a graph is a transformation that produces a mirror image of the original graph across a specific line or point. The line or point across which the reflection occurs is called the axis of reflection.
Graph1
Transform the graph by +4 units in y direction.
f(x)=f(x)+4
Graph2
Transform the graph by +4 units in x direction.
f(x)=f(x-4)
Now take the reflection of graph about x axis
f(x)=-f(x-4)
Graph3
Transform the graph by +7 units in x direction.
f(x)=f(x-7)
Graph5
Transform the graph by -5 units in y direction.
f(x)=f(x)-5
Now Transform the graph by -2 units in x direction.
f(x)=f(x-2)-5
To know more about line, visit:
https://brainly.com/question/30003330
#SPJ1
There are 6 acts in a talent show.
An acrobat, a dancer, a guitarist, a singer, a violinist, and a whistler.
A talent show host randomly schedules the 6 acts.
Compute the probability of each of the following events.
Event A: The acrobat is first, the singer is second, the violinist is third, and the whistler is fourth.
Event B: The first four acts are the whistler, the acrobat, the guitarist, and the dancer, In any order.
Write your answers as fractions in simplest form.
P(A) =
P (B) =
Answers
The probability of Event A is 1/360 and the probability of Event B is 1/15.
For Event A, we can calculate the probability by considering the order in which the acts are scheduled.
There are 6 acts, so there are 6 possible choices for the first act. After the first act is scheduled, there are 5 remaining acts, so there are 5 possible choices for the second act.
Similarly, there are 4 possible choices for the third act, and 3 possible choices for the fourth act.
Finally, there are 2 possible choices for the fifth act, and only 1 choice remains for the last act.
Therefore, the total number of possible ways to schedule all 6 acts is:
6 x 5 x 4 x 3 x 2 x 1 = 720
Since we are only interested in one specific order of the first four acts, we need to count the number of ways to schedule the remaining two acts after the first four have been scheduled in the desired order.
There are 2 remaining acts, so there are 2 possible choices for the fifth act.
Only one act remains for the last slot.
Therefore, the total number of ways to schedule all 6 acts such that the acrobat is first, the singer is second, the violinist is third, and the whistler is fourth is:
1 x 1 x 1 x 1 x 2 x 1 = 2
Thus, the probability of Event A is:
P(A) = 2/720 = 1/360
For Event B, we want to count the number of ways to schedule the first four acts as the whistler, the acrobat, the guitarist, and the dancer, in any order.
There are 4 acts, so there are 4 possible choices for the first act. After the first act is scheduled, there are 3 remaining acts, so there are 3 possible choices for the second act.
Similarly, there are 2 possible choices for the third act, and only one choice remains for the fourth act.
Therefore, the total number of possible ways to schedule the first four acts is:
4 x 3 x 2 x 1 = 24
Since we do not care about the order in which the last two acts are scheduled, we can simply choose any two acts from the remaining 2. There are 2 ways to do this.
Therefore, the total number of ways to schedule all 6 acts such that the first four acts are the whistler, the acrobat, the guitarist, and the dancer, in any order is:
24 x 2 = 48
Thus, the probability of Event B is:
P(B) = 48/720 = 1/15
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
Using Tiles to Multiply Two Binomials
Multiply: (x + 3)(x – 4)

Answers
The middle term in the simplified product for (x + 3)(x – 4) will be B. -x.
How to calculate the binomial?A polynomial with only terms is a binomial. For instance, the binomial x + 2 is composed of the terms x and 2.
Binomial is the name for an algebraic expression with only two terms. It is a polynomial with two terms. It is also referred to as the sum or difference of two or more monomials. It is a polynomial's most basic form.
The product of (x + 3)(x – 4) will be:
= x² - 4x + 3x - 12
= x² - x - 12
In this case, the middle term in the simplified product is -x.
Learn more about binomial on;
https://brainly.com/question/29149158
#SPJ1
How many different ways can the letters " TAGAYTAY WORDS BE ARRANGED?
Answers
Answer:
look it up hahahahah
Step-by-step explanation:
A game card handed out at a grocery store states the probabilities of winning a prize: 0.2 for $10, 0.1 for $5, and 0.7 for $0. What is the probability of winning any amount of money?
Answers
Answer:
Step-by-step explanation:
To calculate the probability of winning any amount of money, we need to sum up the probabilities of winning each individual prize.
Given the probabilities stated on the game card:
Probability of winning $10 prize = 0.2
Probability of winning $5 prize = 0.1
Probability of winning $0 prize = 0.7
To find the probability of winning any amount of money, we add these probabilities together:
0.2 + 0.1 + 0.7 = 1
The sum of the probabilities is 1, which indicates that the total probability of winning any amount of money is 1 or 100%.
Therefore, the probability of winning any amount of money in this game is 100%.
Hope this answer your question
Please rate the answer and
mark me ask Brainliest it helps a lot
Question 1: Use your knowledge of angle relationships to solve for b.
*
30°
b

Answers
Answer:
c. b = 60 degrees
Step-by-step explanation:
Complementary angles, when you add them together, they give 90°. Therefore,
b + 30° = 90°
Solve for b. Subtract 30 from each side
b + 30° - 30° = 90° - 30°
b = 60°
if a straight angle is bisected the resulting angles are what kind of angles?
Answers
If a straight angle is bisected, the resulting angles are 90° and 90°.
What are angle bisectors?Angle bisectors are lines that cut across the angle under consideration. The term "bisect" means to divide into two equal portions. The considered angle is therefore divided in half by the bisected halves.
We have the expression,
a straight angle is bisected.
A straight angle in geometry is one that is 180 degrees in length. It looks like a straight line, which is why it is known as a straight angle.
A straight line may be thought of as a straight angle with two endpoints.
And straight angle has a value of 180°.
When it is bisected,
a straight angle has a bisector that divides it into two equal angles.
It forms 2 angles,
180°/ 2
= 90°
Therefore, resulting angles are 90° and 90°.
Learn more about angle bisector here;
https://brainly.com/question/12896755
#SPJ1
How would you solve
"if f(x) / (x - 2) = x ^ 3 + 2x - 4 + 13/(x - 2) what is f(2)"
and
"if f(x) / (x + 3) = 3x ^ 2 - 4x + 2 what is f(-3)"
Answers
The denominator is zero (0/0 is undefined), we cannot determine the exact value of f(-3) using this equation.
To solve the given equations, we need to find the value of the function f(x) for specific values of x.
"If f(x) / (x - 2) = x³ + 2x - 4 + 13/(x - 2), what is f(2)?"
To find f(2), we can substitute x = 2 into the equation and solve for f(2).
Plugging in x = 2, we get:
f(2) / (2 - 2) = 2³ + 2(2) - 4 + 13/(2 - 2)
Since the denominator is zero (2 - 2 = 0), the equation is undefined. Therefore, there is no solution for f(2) in this case.
"If f(x) / (x + 3) = 3x² - 4x + 2, what is f(-3)?"
To find f(-3), we can substitute x = -3 into the equation and solve for f(-3).
Plugging in x = -3, we get:
f(-3) / (-3 + 3) = 3(-3)² - 4(-3) + 2
Simplifying, we have:
f(-3) / 0 = 3(9) + 12 + 2
f(-3) / 0 = 27 + 12 + 2
f(-3) / 0 = 41
Additional information or context is needed to solve for f(-3).
For similar questions on denominator
https://brainly.com/question/20712359
#SPJ8
In each diagram, line f is parallel to line g, and line t intersects lines f and g
Answers
In each diagram, line f is parallel to line g, and line t intersects both lines f and g. The given information suggests the application of certain geometric properties and relationships.
Firstly, when a transversal line (line t) intersects two parallel lines (lines f and g), it creates several pairs of corresponding angles.
Corresponding angles are congruent, meaning they have equal measures. This property can be used to determine the measures of specific angles in the diagram.
Secondly, when a transversal intersects parallel lines, it also creates alternate interior angles and alternate exterior angles.
Alternate interior angles are congruent, as well as alternate exterior angles.
By utilizing these properties and relationships, one can analyze the diagram and determine the measures of various angles.
It is important to measure angles systematically and compare them to find congruent or equal measures.
For more such questions on geometric properties
https://brainly.com/question/23949211
#SPJ8
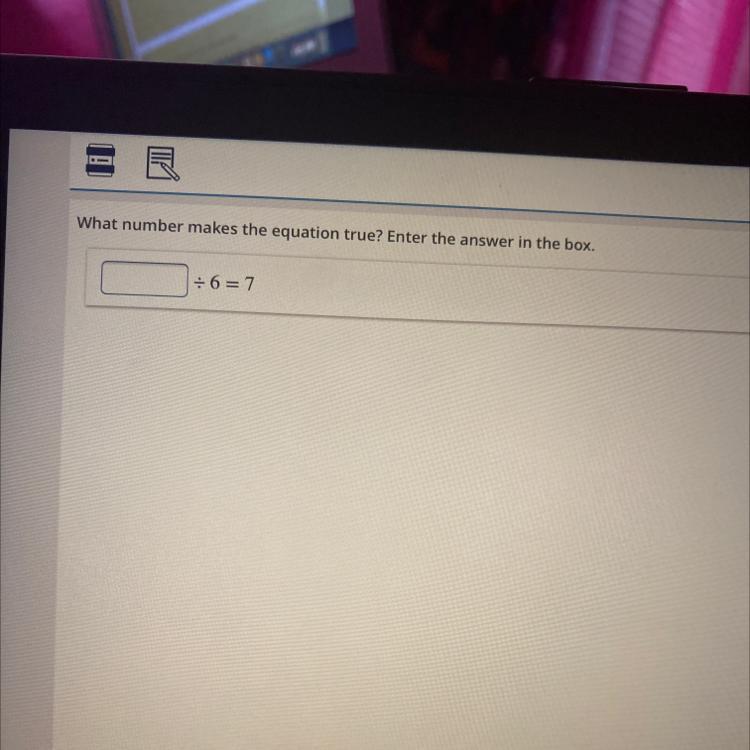
division 6=7??????????
Answers
Can somebody help me, I'm being timed!

Answers
Answer:
I think its -- linear postulate
Step-by-step explanation:
(5k+35) -8=12 need help solving this
Answers
Answer:
k= -6.48 approx
Step-by-step explanation:
(5k+35) -8=12
opening bracket
-45k-280=12
-45k=12+280
-45k=292
k=-6.48 approx
Answer:
Step-by-step explanation:
I don't say you have to mark my ans as brainliest but if you think it has really helped you plz don't forget to thank me...

Interpret the 95% confidence interval for average BMI. What do the lower and upper bounds of the confidence interval tell us?
Answers
Answer:
(26.2252 ; 27.3748)
Step-by-step explanation:
The confidence interval is given by :
x ± Margin of error
The margin of error = Zcritical * (σ/√(n))
σ = 7.5 ; n = 654
Zcritical = Zα/2 = 1.96
The margin of error = 1.96 * (7.5/√654) = 0.5748
The confidence interval :
Upper boundary = 26.8 + 0.5748 = 27.3748
Lower boundary = 26.8 - 0.5748 = 26.2252
(26.2252 ; 27.3748)
We are 95% confident that the mean BMI of the entire population will fall in between (26.2252 ; 27.3748)
Let give the number of liters of fuel oil burned in hours, and the number of gallons burned. Find a formula for by scaling the output of . Use the fact that 1 gallon equals 3.785 liters. You may enter the function verbatim, as you would for any other named function.
Answers
Answer: To convert liters of fuel oil burned in hours to gallons, we can use the conversion factor that 1 gallon is equal to 3.785 liters. The formula for the conversion can be represented as a function:
def liters_to_gallons(liters):
return liters / 3.785
Here, the input liters represents the number of liters of fuel oil burned in hours, and the output of the function is the equivalent number of gallons. The function performs the conversion by dividing the input value (in liters) by the conversion factor (3.785).
Adam, Barry, and Charles visited a small farmers market last Saturday. Adam purchased 3 dozen eggs, 1 wheel of cheese, and 5 pounds of potatoes. Barry bought 1 dozen eggs and 10 pounds of potatoes, while Charles purchased 2 dozen eggs and 2 pounds of potatoes. If Adam’s bill was $38.25, Barry’s $36.50 and Charles’ $17.20, how much did a dozen eggs, a wheel of cheese and a pound of potatoes cost?
Answers
Answer:
Dozen eggs = $5.5
Wheel of cheese = $6.25
Pound of potatoes = $3.1
Step-by-step explanation:
Let the cost
Dozen of egg = x
Wheel of cheese = y
Pound of potato = z
We will form linear equations using the information given in the question
Adam purchased 3 dozen eggs, 1 wheel of cheese, and 5 pounds of potatoes
3x + y + 5z = 38.25 ................(1)
Barry bought 1 dozen eggs and 10 pounds of potatoes
x + 10z = 36.50 ............(2)
Charles purchased 2 dozen eggs and 2 pounds of potatoes
2x + 2z = 17.20 .................(3)
solving 2 and 3
x = $5.5 and z = $3.1
substitute these values in equation 1
we get
y = $6.25
The cost
Dozen eggs = $5.5
Wheel of cheese = $6.25
Pound of potatoes = $3.1