Find the value of k so that (x^4-2x^2+kx+6) is divided by (x-2) , the remainder is 0.
Answers
To solve this questio, we have to divide the given polynomial by the binomial as normal:
At this point, we have to continue with the division:
For the last term of the quotient we use the following reasoning: We need a number that when multiplied by -2 the result is 6, that way the remainder will be 0. That number is -3. When multiplying -3 by x we obtain -3x. It means that (2+k)x has to be equal to -3x. Use this information to find the value of k:
\(\begin{gathered} (2+k)x=-3x \\ 2+k=-3 \\ k=-3-2 \\ k=-5 \end{gathered}\)It means that k has a value of -5.
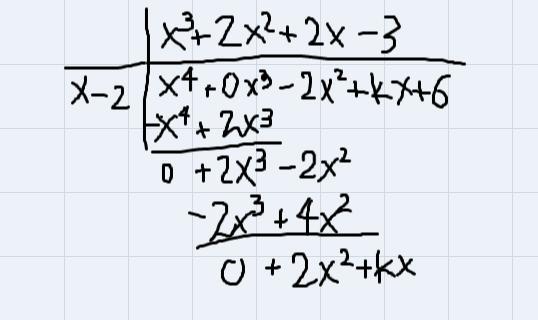
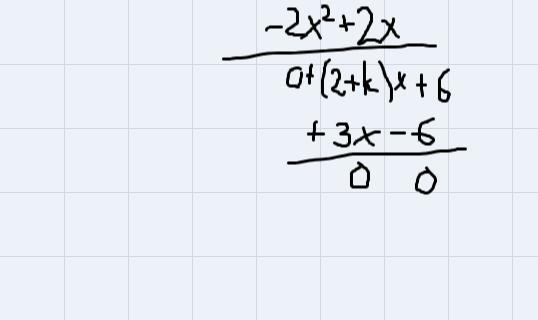
Related Questions
What is the volume of a right circular cylinder with a diameter of 6 meters and a height of 14 meters. Leave the answer in terms of π.
504π m3
396π m3
126π m3
84π m3
Answers
The volume of a right circular cylinder with a diameter of 6 meters and a height of 14 meters as required is; 54π.
What is the volume of the cylinder?It follows from the task content that the volume of a cylinder whose diameter is 6 meters and height is 14 meters.
Since the volume of a right circular cylinder is given by; V = πr²h.
since Diameter is; 6 ft. Radius, r = 6/2 = 3 meters.
Volume, V = π (3)² 6; V = π × 9 × 6
Volume, V = 54π.
Ultimately, the volume of the right circular cylinder is; 54π m³.
Read more on volume of a cylinder;
https://brainly.com/question/27535498
#SPJ1
PLS ANSWER THESE QUESTIONS
I WILL MARK BRAINLIEST

Answers
The linear function y = 3 · w - 1 represents the number of sea shells found in each week.
The speed of the driven gear is 180 rounds per minute.
How to use direct and inverse relationships to analyze situations
In the first problem we have an example of linear progression, in which the number of sea shells is increased linearly every week. After a quick analysis, we conclude that the linear function y = 3 · w - 1, a kind of direct relationship.
In the second problem, we must an inverse relationship to determine the speed of the driven gear. Please notice that the speed of the gear is inversely proportional to the number of teeths. Then, we proceed to calculate the speed:
\(\frac{v_{1}}{v_{2}} = \frac{N_{2}}{N_{1}}\)
If we know that \(v_{2} = 60\,rpm\), \(N_{2} = 60\) and \(N_{1} = 20\), then the speed of the driven gear is:
\(v_{1} = v_{2}\times \frac{N_{2}}{N_{1}}\)
\(v_{1} = 60\,rpm \times \frac{60}{20}\)
\(v_{1} = 180\,rpm\)
The speed of the driven gear is 180 rounds per minute.
To learn more on inverse relationships: https://brainly.com/question/4147411
#SPJ1
Insurance claims An insurance company claims annual loss from fire is μ = $250 with a standard that in the population of homeowners, the mean deviation of o = $5000. The distribution of loss is strongly right-skewed: Many policies have $0 loss, but a few have large losses.
Answers
For a large sample size (greater than 30), distribution is normal.
How to solveAn insurance company claims that in the population of homeowners, the mean loss and standard deviation from fire is
μ = $250
o = $5000
The distribution of loss is strongly right skewed.
a). Since for a simple random sample of size n= 15 drawn from the population of homeowners.
Since the given sample size is small. Therefore for small sample size less the 30 the distribution of
follow t- distribution.
Since t distribution has more variance than normal distribution.
Also t- distribution is symmetric as normal distribution at t=0.
For small sample size sampling distribution is t -distribution.
b). Now if the simple random sample of size n = 10000 drawn from the population of homeowners.
Thus for the large sample size and given mean and standard deviation sampling distribution of x follow normal distribution. Also we know that normal distribution have a bell-shaped curve which is symmetric to z=0.
For a large sample size (greater than 30), distribution is normal.
Read more about standard deviation here:
https://brainly.com/question/475676
#SPJ1

Final question - whats the answer?

Answers
Answer: 7^5 or 7 to the fifth power.
Step-by-step explanation: This is an exponent meaning you count the 7’s and in the first picture there’s 5 7’s. This means that the number your putting to a power is the yellow box so that’s 7 and the exponent is 5 not 4 because if you did 7 to the first power it’s still 7 so it would be 7 to the 5th power or 7^5
6(2) - 7(8 + 6 - 3(2)
Answers
Answer:
-44
Step-by-step explanation:
12-7(8+6-6)
12-7(8)
12-56
-44
Step-by-step explanation:
6(2)-7(8+6-3(2))
12-7(8+6-6)
12-7(8)
12-56
-44
hope it's helpful ❤❤❤❤❤❤
THANK YOU.
#
I don’t understand what I really have to do

Answers
H
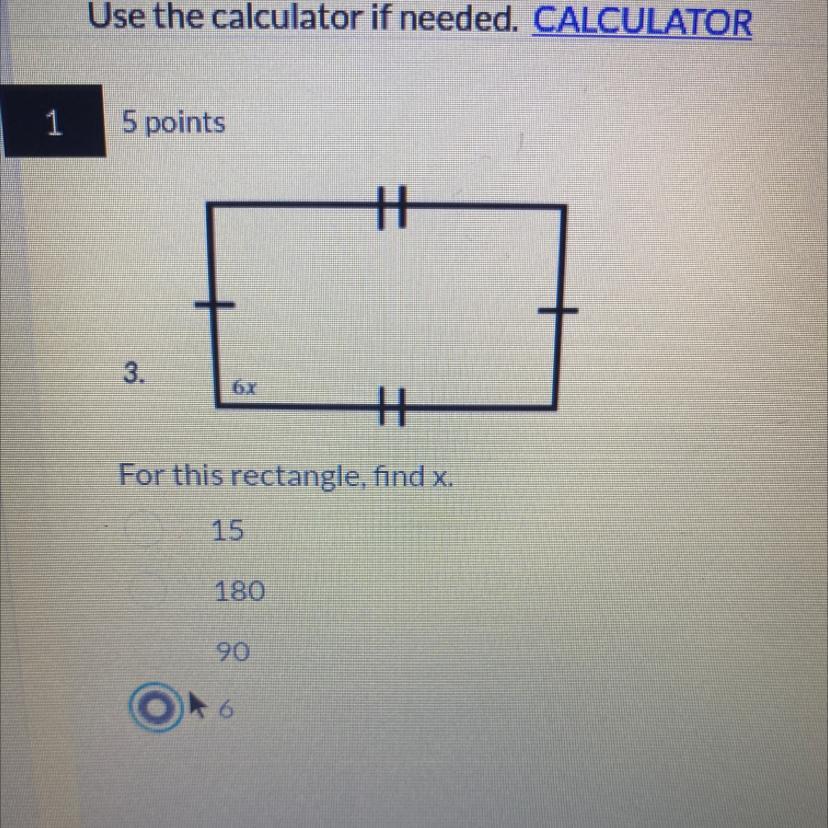
3.
6x
++
For this rectangle, find x.
15
180
90
6
k
Answers
Answer:
x =15
Step-by-step explanation:
its a rectangle all interior angles must be equal to 90 so 6x=90
divide by 6 to get x on its own and you get 15
Find the value of f (3)
y =f(x)
Please help

Answers
Answer:
f=7/3
Step-by-step explanation:
from the figure it can be deduced that x=3 and
y=7
so: y=f(x) → 7=f(3)
put f to the first member: 7=3f → 3f=7 → f=7/3
(I hope that's right)
Answer:
f(3) = 7
Step-by-step explanation:
locate x = 3 on the x- axis, then go vertically up to meet the line at (3, 7) , so
f(3) = 7
find the square root of 7
Answers
The value of the square root of 7 is,
⇒ √7 = 2.645
What is mean by Function?A relation between a set of inputs having one output each is called a function. and an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
WE have to given that;
To find the value of the square root of 7 .
Since, the square root of 7 is,
⇒ √ 7
⇒ 2.645
Thus, The value of the square root of 7 is,
⇒ √7 = 2.645
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ5
Review the graph of function g(x). On a coordinate plane, y = g (x) curves down through (negative 5, 2), has an inflection point at (0, negative 3), and curves down through (5, negative 6). Which point is on the graph of the inverse function g–1(x)?

Answers
Answer:
A. (–3, 0)
Step-by-step explanation:
......
The point through which the graph of g-1(x) passes is (-3,0) which is option (A).
What is the inverse of a function?An inverse function or an anti function is defined as a function, which can reverse into another function.
What is point of inflection?The graph of a function changes concavity at inflection points (or points of inflection.
The point (0,-3) is lying on the graph y = g(x), now when we have to find a point lying on y = g-1(x) , the coordinates of this point will reverse as it is the point of inflection. So the coordinates of the point lying of y = g-1(x) will be (-3,0).
Learn more about Inverse of Function on:
https://brainly.com/question/11735394
#SPJ2
(question 15) Find the derivative of the function
using logarithmic differentiation.

Answers
Answer:
\(\textsf{A.} \quad (2+x)^x\left[\dfrac{x}{2+x}+\ln(2+x)\right]\)
Step-by-step explanation:
Replace f(x) with y in the given function:
\(y=(x+2)^x\)
Take natural logs of both sides of the equation:
\(\ln y=\ln (x+2)^x\)
\(\textsf{Apply the log power law to the right side of the equation:} \quad \ln a^n=n \ln a\)
\(\ln y=x\ln (x+2)\)
Differentiate using implicit differentiation.
Place d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}\ln y=\dfrac{\text{d}}{\text{d}x}x\ln (x+2)\)
First, use the chain rule to differentiate terms in y only.
In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}=\dfrac{\text{d}}{\text{d}x}x\ln (x+2)\)
Now use the product rule to differentiate the terms in x (the right side of the equation).
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let}\; u=x \implies \dfrac{\text{d}u}{\text{d}x}=1\)
\(\textsf{Let}\; v=\ln(x+2) \implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{1}{x+2}\)
Therefore:
\(\begin{aligned}\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}&=x\cdot \dfrac{1}{x+2}+\ln(x+2) \cdot 1\\\\\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}&= \dfrac{x}{x+2}+\ln(x+2)\end{aligned}\)
Multiply both sides of the equation by y:
\(\dfrac{\text{d}y}{\text{d}x}&=y\left( \dfrac{x}{x+2}+\ln(x+2)\right)\)
Substitute back in the expression for y:
\(\dfrac{\text{d}y}{\text{d}x}&=(x+2)^x\left( \dfrac{x}{x+2}+\ln(x+2)\right)\)
Therefore, the differentiated function is:
\(f'(x)=(x+2)^x\left[\dfrac{x}{x+2}+\ln(x+2)\right]\)
\(f'(x)=(2+x)^x\left[\dfrac{x}{2+x}+\ln(2+x)\right]\)
Find the midpoint of the segment with the given endpoints. (-7,-4) and (3,7)?
Answers
9514 1404 393
Answer:
(-2, 1.5)
Step-by-step explanation:
The coordinates of the midpoint are the average of the end point coordinates:
((-7, -4) +(3, 7))/2 = (-7+3, -4+7)/2 = (-4, 3)/2 = (-2, 1.5)
The coordinates of the midpoint are (-2, 1.5).

The points J (9,7), K (2,1), L(0,−8) and M (7,−2) form quadrilateral JKLM.
Plot the points
slope of JK =
length of JK =
slope of KL =
length of KL =
slope of LM =
length of LM =
slope of MJ =
length of MJ =
Quadrilateral JKLM can BEST be described as
Answers
Quadrilateral JKLM has sides with equal lengths (√85), and the slopes of opposite sides are equal. However, it is not a special type of quadrilateral like a rectangle or a square.
To describe quadrilateral JKLM, let's first plot the given points J(9, 7), K(2, 1), L(0, -8), and M(7, -2) on a coordinate plane:
J(9, 7) K(2, 1)
L(0, -8) M(7, -2)
To find the slopes and lengths of each side of the quadrilateral, we can use the distance formula and the slope formula.
Slope of JK:
Slope (m) = (change in y) / (change in x)
m(JK) = (7 - 1) / (9 - 2) = 6/7
Length of JK:
Length (d) = √[(x2 - x1)^2 + (y2 - y1)^2]
d(JK) = √[(9 - 2)^2 + (7 - 1)^2] = √(49 + 36) = √85
Slope of KL:
m(KL) = (-8 - 1) / (0 - 2) = -9/2
Length of KL:
d(KL) = √[(0 - 2)^2 + (-8 - 1)^2] = √(4 + 81) = √85
Slope of LM:
m(LM) = (-2 - (-8)) / (7 - 0) = 6/7 (same as slope of JK)
Length of LM:
d(LM) = √[(7 - 0)^2 + (-2 - (-8))^2] = √(49 + 36) = √85
Slope of MJ:
m(MJ) = (7 - (-2)) / (9 - 7) = 9
Length of MJ:
d(MJ) = √[(7 - 9)^2 + (-2 - (-8))^2] = √(4 + 36) = √40
Based on the calculations, we can describe quadrilateral JKLM as follows:
The slope of JK and LM is 6/7.
The slope of KL is -9/2.
The slope of MJ is 9.
The length of each side (JK, KL, LM, MJ) is √85.
The quadrilateral is not a rectangle or a square since the slopes of opposite sides (JK and LM) are not perpendicular.
For more such question on Quadrilateral. visit :
https://brainly.com/question/23935806
#SPJ8
The distance from the tip of a slice of pizza to the crust is 7 inches.
Does this represent diameter, circumference, or radius?
ANSWER ASAP THANK YOU
Answers
Answer:
radius
Step-by-step explanation:
Hey can anyone help pls and thank you
Answers
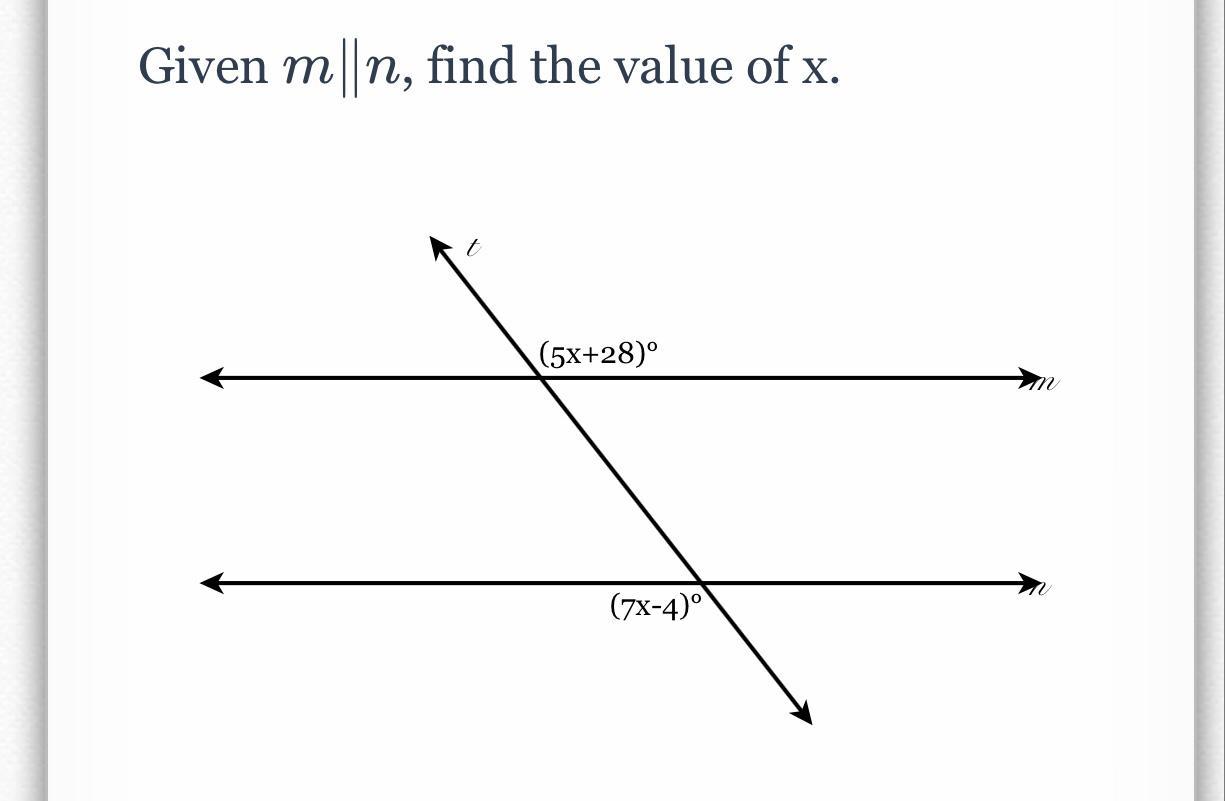
Answer:
5x+28=7x-4
5x+32=7x
32=2x
x=16
Hope This Helps!!!
Answer:
x = 16
Step-by-step explanation:
(7x - 4) and (5x + 28) are alternate exterior angles and are congruent, so
7x - 4 = 5x + 28 ( subtract 5x from both sides )
2x - 4 = 28 ( add 4 to both sides )
2x = 32 ( divide both sides by 2 )
x = 16
Which ordered pair lies on the function f(x) = x2 + 3?
A) (–1,4)
B) (–1,–4)
C) (1,–4)
D) (–4,–1)
Answers
Answer:
(-1,4)
Step-by-step explanation:
to find out we just fill in the values to see if it’s true
(x,f(x))
4=-1^2+3
4=1+3
4=4
True
-4=-1^2+3
-4=1+3
-4=4
Not true
-4=1^2+3
-4=1+3
-4=4
Not true
-1=-4^2+3
-1=16+3
-1=19
Not true
Hopes this helps please mark brainliest
For which function defined by a
polynomial are the zeros of the
polynomial -3,0, and 4?
1) f(x)=(x+3)(x +4)
2) f(x)=(x² - 3)(x-4)
3) f(x)= x(x+3)(x-4)
4) f(x)= x(x − 3)(x +4)
Answers
Answer:
Option 3
Step-by-step explanation:
If we are given roots of a polynomial, r and q. We can represent the roots as
\((x - r)(x - q)\)
The roots here are 0, -3and 4 so the roots are
\(x(x - ( - 3)(x - 4)\)
Which equal to
\(x(x + 3)(x - 4)\)
Option 3 is the answer
Perform the given translation on the point (2,-5) translation 5 units left, then 3 units up
Answers
Answer:
(2, -5) becomes (7, -2)
Step-by-step explanation:
We start with (2, -5). Translating this point 5 units to the left results in the new x-coordinate 2 + 5, or 7; translating (7, -5) 3 units up results in the new y-coordinate -5 + 3, or -2:
start: (2, -5)
finish: (7, -2)
whats the slope of this??

Answers
Answer:
slope= 2
Step-by-step explanation:
y^2-y^1/z^2-x^1
9-3/6-3
6/3=2
Determine whether the following individual events are independent or dependent. Then find the probability of the combined event.
In a town where 1/4 of the days are sunny and 3/4 are cloudy, the next six days are all sunny.
Answers
The probability of the combined event that the next six days are all sunny is 1/4096
How to determine the probability all days being sunny?From the question, we have the following parameters that can be used in our computation:
Probability that it is sunny = 1/4
Probability that it is cloudy = 3/4
Number of days = 6
The probability for all six days, it is sunny is represented as
Probability = Probability that it is sunny^Number of days
Substitute the known values in the above equation, so, we have the following representation
Probability = (1/4)⁶
Express as decimal
Probability = (0.25)⁶
Evaluate the exponent
Probability = 1/4096
Hence, the probability is 1/4096
Read more about probability at
https://brainly.com/question/251701
#SPJ1
let f(x) = (3x^3+17)^3 and g(x) = 3x^3 + 17. given that f(x) = (h*g)(x) find h(x)
Answers
We have that f(x) and g(x) are defined as:
\(\begin{gathered} f(x)=(3x^3+17)^3 \\ g(x)=3x^3+17 \end{gathered}\)If f(x) is also related to h(x) and g(x) as:
\(f(x)=(h\cdot g)(x)\)We can then find h(x) as:
\(\begin{gathered} f(x)=h(x)\cdot g(x) \\ h(x)=\frac{f(x)}{g(x)} \end{gathered}\)If we replace f(x) and g(x) we obtain:
\(h(x)=\frac{f(x)}{g(x)}=\frac{(3x^3+17)^3}{3x^3+17}=(3x^3+17)^2\)Answer: h(x) = (3x^3 + 17)^2
Find the value of a. Round to the nearest tenth, if necessary. 11 24 a

Answers
Answer:
21.3
Step-by-step explanation:
It's easier to see how to do this if you transfer the 11 to the bottom of the rectangle. The look at the left triangle. It has 3 sides.
24, 11, and a.
You should be able to find a using
a^2 + 11^2 = 24^2 Expand the squares
a^2 + 121 = 576 Subtract 121 from both sides
a^2 = 576 - 121
a^2 = 455 Take the square root of both sides.
sqrt(a^2) = sqrt(455)
a = 21.33
or
a = 21.3
A woman deposits $300 in a savings account that pays 6% annually. If she withdraws all the money in the account after 120 days, how much does she withdraw (rounded to the nearest dollar)?
Answers
The woman will withdraw $300 given 6% interest rate annually.
We can use the formula for simple interest to solve this problem:
I = Prt
where I is the interest earned, P is the principal (initial deposit), r is the annual interest rate as a decimal, and t is the time in years. Since the interest rate is given as an annual rate, we need to convert it to a daily rate by dividing by 365:
r = 0.06/365 = 0.00016438356
The time in years is 120/365 = 0.3287671233 years. Now we can plug in the values and solve for I:
I = 300 * 0.00016438356 * 0.3287671233 = 0.01699999999
The interest earned is $0.017, which is negligible. Therefore, the woman will withdraw the entire principal plus any interest earned, which is:
300 + 0.017 = $300.02
Rounding to the nearest dollar, the woman will withdraw $300.
To learn more about interest rate here:
https://brainly.com/question/29067327
#SPJ1
If f(x) = 2x2 - 5 and g(x) = 3x + 3, find (f - g)(x).
A. 3x – 2x2 - 2
B. 2x2 – 3x - 2
C. 2x2 – 3x-8
D. - x² – 8
Answers
Answer:
2x^2 -3x -8
Step-by-step explanation:
f(x) = 2x^2 - 5
g(x) = 3x + 3,
(f - g)(x)= 2x^2 - 5 -(3x + 3)
Distribute the minus sign
(f - g)(x)= 2x^2 - 5 -3x - 3
Combine like terms
= 2x^2 -3x -8
Which relationship describes angles 1 and 2?
1. Vertical Angles 2. Complementary Angles 3. Supplementary Angles 4. Adjacent Angles

Answers
Pls I don't understand

Answers
The unit rate of the relationship will be 10/3. The correct option is C.
The given equation is,
y = 10/3x + 8
The general form of an equation of the line is,
y = mx + c
here, the slope will be 10/3
Slope refers to the steepness or incline of a line on a graph. It is a measure of how much the dependent variable changes for a given change in the independent variable.
The slope of a line is represented by the ratio of the change in the y-axis (vertical) to the change in the x-axis (horizontal) between any two points on the line. It can also be interpreted as the rate of change of the dependent variable with respect to the independent variable.
A positive slope indicates an upward trend, while a negative slope indicates a downward trend. The slope of a line is often denoted by the letter m.
The unit relationship will be 10/3.
To know more about slope follow
https://brainly.com/question/19131126
#SPJ1
2/3 : 3/2 : 5/8 how to do this?
Answers
Answer:
The simplified ratio will be 16:36:15
Step-by-step explanation:
\(2/3:3/2:5/8\\\)
multiply all terms by 8,
\(8(2/3):8(3/2):8(5/8)\\= 16/3:12:5\)
Now, multiply each term by 3
\(3(16/3):3(12):3(5)\\\\16:36:15\)
Lara and Hayden volunteer at an animal shelter. Lara already volunteered 50 hours and will volunteer 5 hours more each week. Hayden already volunteered to hours and will volunteer 10 hours each week . At these rates, how many will it take Lara and Hayden to volunteer the same number of ?
Answers
There are 8 to take Lara and Hayden to volunteer the same number.
What is Mathematical expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
Lara already volunteered 50 hours and will volunteer 5 hours more each week.
And, Hayden already volunteered to 10 hours and will volunteer 10 hours each week .
Now, For Lara;
⇒ 50 + 5x
And, For Hayden;
⇒ 10 + 10x
So, For same number of volunteer is,
⇒ 50 + 5x = 10 + 10x
⇒ 50 - 10 = 10x - 5x
⇒ 40 = 5x
⇒ x = 40/5
⇒ x = 8
Thus, There are 8 to take Lara and Hayden to volunteer the same number.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
Triangle ABC with vertices at A(4, 3), B(3, −2), C(−3, 1) is dilated using a scale factor of 1.5 to create triangle A′B′C′. Determine the vertex of point A′.
Answers
The vertex of point A' in the dilated triangle A'B'C' is (6, 4.5).
1. Start by calculating the distance between the vertices of the original triangle ABC:
- Distance between A(4, 3) and B(3, -2):
Δx = 3 - 4 = -1
Δy = -2 - 3 = -5
Distance = √((-\(1)^2\) + (-\(5)^2\)) = √26
- Distance between B(3, -2) and C(-3, 1):
Δx = -3 - 3 = -6
Δy = 1 - (-2) = 3
Distance = √((-6)² + 3²) = √45 = 3√5
- Distance between C(-3, 1) and A(4, 3):
Δx = 4 - (-3) = 7
Δy = 3 - 1 = 2
Distance = √(7² + 2²) = √53
2. Apply the scale factor of 1.5 to the distances calculated above:
- Distance between A' and B' = 1.5 * √26
- Distance between B' and C' = 1.5 * 3√5
- Distance between C' and A' = 1.5 * √53
3. Determine the coordinates of A' by using the distance formula and the given coordinates of A(4, 3):
- A' is located Δx units horizontally and Δy units vertically from A.
- Δx = 1.5 * (-1) = -1.5
- Δy = 1.5 * (-5) = -7.5
- Coordinates of A':
x-coordinate: 4 + (-1.5) = 2.5
y-coordinate: 3 + (-7.5) = -4.5
4. Thus, the vertex of point A' in the dilated triangle A'B'C' is (2.5, -4.5).
For more such questions on triangle, click on:
https://brainly.com/question/1058720
#SPJ8
What is the greatest common factor of 24s3, 12s4, and 18s?
Answers
Answer:
24
Step-by-step explanation: