Answers
Answer:
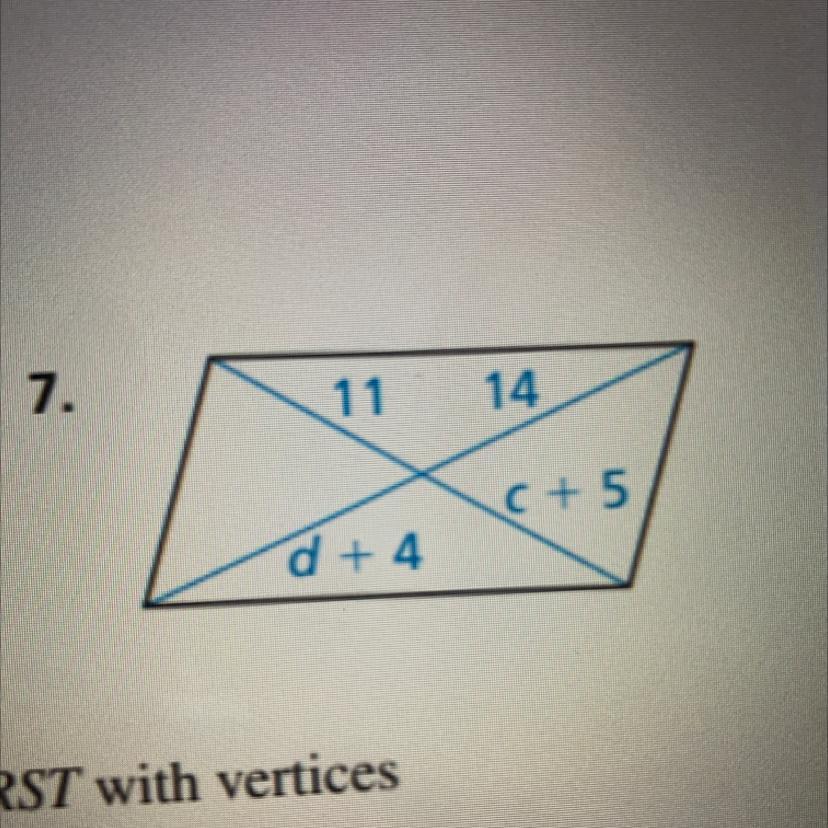
C = 6
D = 10
Step-by-step explanation:
C + 5 = 11
C + 5 -5 = 11 -5
C = 6
D + 4 = 14
D + 4 -4 = 14 -4
D = 10
Related Questions
Jabal and Michael are walking to school and agree to leave their homes at the same time.
Jabal leaves his house walking 2.5 meters per second. Michael leaves his house walking 5 meters per second.
Jabal's house is 15 meters closer to school than Michael's house, therefore he is starting 15 meters closer than Michael.
After how long are the boys walking together? Use any strategy you'd like to solve.
Answers
Answer: 6 seconds
Step-by-step explanation:
Time Jabal (2.5mps) Michael (5mps)
Start 15 0
1 sec 17.50 5
2 20 10
3 22.5 15
4 25 20
5 27.5 25
6 30 30
7
8
9
10
Answer:
6 sec
Step-by-step explanation:
Let d = distance for Jabal
d + 15 = distance for Michael
t = d/r
d/2.5 = time for Jabal
(d + 15)/5 = time for Michael
The times are equal since they both started walking at the same time.
(d + 15/5 = d/2.5
2.5(d + 15) = 5d
2.5d + 37.5 = 5d
37.5 = 2.5d
d = 15 m. = Jabal's distance
15/2.5 = 6 sec.
Ryan has a collection of 220 baseball cards he letshis brother have 1/4 of his collection until 20% of his collection to the baseball card shop she takes 15 cards to school to give his friend how many baseball cards remaining Ryan's collection
Answers
Stu had quite a collection of baseball cards. One day he decided to give half of them to his brother Seth. Then he gave one-third of what he had left to a friend. Then he gave half of what was left to another friend. Stu now has 50 baseball cards. How many did he start with? It seems that I should work
let Stu have x cards
he gave half to seth
so he had x/2 cards
He had x/2 he gave 1/3 of x/2 to a friend
=x/6.
Now he had x/2 - x/6 = x/3 with him balance
1/2 of x/3 he gave to another friend =x/6
Balance he had was x/3 - x/6 = x/6
x/6 = 50
multiply by 6
x= 300
Answer:
Now he had x/2 - x/6 = x/3 with him balance
1/2 of x/3 he gave to another friend =x/6
Balance he had was x/3 - x/6 = x/6
x/6 = 50
multiply by 6
x= 300
Step-by-step explanation:
The position of a particle moving along the x axis varies in time according to the expression x=3t2, where x is in meters and t is in seconds. Evaluate its position at the following times. (a) t=3.30 s m (b) t=3.30 s+Δt xf=m (c) Evaluate the limit of Δx/Δt as Δt approaches zero to find the velocity at t=3.30 s. m/s
Answers
Given information:Position of a particle moving along the x-axis varies in time according to the expression x = 3t², where x is in meters and t is in seconds.
To determine the position at the following times. a. t = 3.30 s, b. t = 3.30 s + Δt xf and c. Evaluate the limit of Δx/Δt as Δt approaches zero to find the velocity at t = 3.30 s. a. To find the position when t = 3.30 s, substitute t = 3.30 s in x = 3t².x = 3t² = 3(3.30)² = 32.67 metersTherefore, the position at t = 3.30 s is 32.67 meters.
b. To find the position when t = 3.30 s + Δt, substitute t = 3.30 s + Δt in x = 3t².x = 3t² = 3(3.30 s + Δt)² = 3(10.89 + 6.6Δt + Δt²) = 32.67 + 19.8Δt + 3Δt²Therefore, the position when t = 3.30 s + Δt is 32.67 + 19.8Δt + 3Δt².c. Velocity is given by Δx/Δt.Δx/Δt = [x(t + Δt) - x(t)]/ΔtBy substituting the given values, we have;Δx/Δt = [x(3.30 + Δt) - x(3.30)]/Δt= [3(3.30 + Δt)² - 3(3.30)²]/Δt= 19.8 + 6ΔtTaking the limit of Δx/Δt as Δt → 0, we have;Δx/Δt = 19.8 + 6(0)Δt = 19.8Therefore, the velocity at t = 3.30 s is 19.8 m/s.
To know more about Position visit:
https://brainly.com/question/23709550
#SPJ11
Ace makes an 8% commission on any artwork that he sells. If he sells $125 wroth of artwork, how much commission does he get.
I will give brainly
Answers
Answer:
10
Step-by-step explanation:
125 x .08 = 10
A home security system may detect movement using its two different sensors. If motion is detected by any of the sensors, the system will alert the police. If there is movement outside, sensor V (video camera) will detect it with probability 0.95, and sensor L (laser) will detect it with probability 0.8. If there is no movement outside, sensor L will detect motion anyway with probability 0.05, and sensor V will detect motion anyway with probability 0.1. Based on past history, the probability that there is movement at a given time is 0.7. Assume these sensors have proprietary algorithms, so that conditioned on there being movement (or not), the events of detecting motion (or not) for each sensor is independent.
(a) Given that there is movement outside and that sensor V does not detect motion, what is the probability that sensor L detects motion?
(b) Given that there is a moving object, what is the probability that the home security system alerts the police?
(c) What is the probability of a false alarm? That is, that there is no movement but the police are alerted anyway?
(d) What is the probability that there is a moving object given that both sensors detect motion?
Answers
d) Tthe probability that there is a moving object given that both sensors detect motion is approximately 0.98.
(a) To find the probability that sensor L detects motion given that there is movement outside and sensor V does not detect motion, we can use Bayes' theorem.
Let's denote the events as follows:
A = Movement outside
B = Sensor V does not detect motion
C = Sensor L detects motion
We are given:
P(A) = 0.7 (probability of movement outside)
P(B|A) = 0.05 (probability of sensor V not detecting motion given movement outside)
P(C|A) = 0.8 (probability of sensor L detecting motion given movement outside)
We want to find P(C|A', B), where A' denotes the complement of event A.
Using Bayes' theorem:
P(C|A', B) = [P(A' | C, B) * P(C | B)] / P(A' | B)
We can calculate the values required:
P(A' | C, B) = 1 - P(A | C, B) = 1 - P(A ∩ C | B) / P(C | B) = 1 - [P(A ∩ C ∩ B) / P(C | B)]
= 1 - [P(B | A ∩ C) * P(A ∩ C) / P(C | B)]
= 1 - [P(B | C) * P(A) * P(C | A) / P(C | B)]
= 1 - [P(B | C) * P(A) * P(C | A) / [P(B | C) * P(A) * P(C | A) + P(B | C') * P(A') * P(C | A')]]
P(B | C) = 0 (since sensor V does not detect motion when there is motion outside)
P(C | A') = 0 (since sensor L does not detect motion when there is no motion outside)
Substituting these values:
P(C | A', B) = 1 - [0 * P(A) * P(C | A) / (0 * P(A) * P(C | A) + P(B | C') * P(A') * P(C | A'))]
= 1 - [0 / (0 + P(B | C') * P(A') * P(C | A'))]
= 1 - 0
= 1
Therefore, the probability that sensor L detects motion given that there is movement outside and sensor V does not detect motion is 1.
(b) To find the probability that the home security system alerts the police given that there is a moving object, we need to consider the different combinations of sensor detections.
Let's denote the events as follows:
D = The home security system alerts the police
M = There is a moving object
We need to calculate P(D | M). This can occur in two ways:
1. Both sensor V and sensor L detect motion.
2. Sensor L detects motion while sensor V does not.
Using the law of total probability:
P(D | M) = P(D, V detects motion, L detects motion | M) + P(D, V does not detect motion, L detects motion | M)
We know:
P(D, V detects motion, L detects motion | M) = P(V detects motion | M) * P(L detects motion | M) = 0.95 * 0.8 = 0.76
P(D, V does not detect motion, L detects motion | M) = P(V does not detect motion | M) * P(L detects motion | M) = (1 - 0.95) * 0.8 = 0.04
Substituting
these values:
P(D | M) = 0.76 + 0.04
= 0.8
Therefore, the probability that the home security system alerts the police given that there is a moving object is 0.8.
(c) To find the probability of a false alarm, i.e., that there is no movement but the police are alerted anyway, we need to consider the different combinations of sensor detections.
Let's denote the events as follows:
D = The home security system alerts the police
NM = There is no movement
We need to calculate P(D | NM). This can occur in two ways:
1. Both sensor V and sensor L detect motion.
2. Sensor L detects motion while sensor V does not.
Using the law of total probability:
P(D | NM) = P(D, V detects motion, L detects motion | NM) + P(D, V does not detect motion, L detects motion | NM)
We know:
P(D, V detects motion, L detects motion | NM) = P(V detects motion | NM) * P(L detects motion | NM) = 0.1 * 0.05 = 0.005
P(D, V does not detect motion, L detects motion | NM) = P(V does not detect motion | NM) * P(L detects motion | NM) = (1 - 0.1) * 0.05 = 0.045
Substituting these values:
P(D | NM) = 0.005 + 0.045
= 0.05
Therefore, the probability of a false alarm, i.e., that there is no movement but the police are alerted anyway, is 0.05.
(d) To find the probability that there is a moving object given that both sensors detect motion, we can use Bayes' theorem.
Let's denote the events as follows:
M = There is a moving object
V = Sensor V detects motion
L = Sensor L detects motion
We want to find P(M | V, L).
Using Bayes' theorem:
P(M | V, L) = [P(V, L | M) * P(M)] / [P(V, L)]
We can calculate the values required:
P(V, L | M) = P(V | M) * P(L | M) = 0.95 * 0.8 = 0.76
P(M) = 0.7 (given probability of movement)
P(V, L) = P(V, L | M) * P(M) + P(V, L | M') * P(M')
= 0.76 * 0.7 + 0.04 * 0.3
= 0.532 + 0.012
= 0.544
Substituting these values:
P(M | V, L) = (0.76 * 0.7) / 0.544
≈ 0.98
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
Pls urgent help needed Bcz exam tmrw

Answers
The simplification of the expression 4a + 3b - a + 3b + 6 is 3(a + 2b + 2)
The expression im terms of x for the perimeter of the triangle is 31 = (3x - 5) + (2x - 1) + (x + 1)The value of x is 6How to find the perimeter of a triangle?Simplify 4a + 3b - a + 3b + 6
collect like terms
= 4a - a + 3b + 3b + 6
= 3a + 6b + 6
factorize
= 3(a + 2b + 2)
side a = 3x - 5
side b = 2x - 1
side c = x + 1
Perimeter = 31 cm
The perimeter of a triangle = side a + side b + side c
31 = (3x - 5) + (2x - 1) + (x + 1)
31 = 3x - 5 + 2x - 1 + x + 1
31 = 6x - 5
Add 5 to both sides
31 + 5 = 6x
36 = 6x
divide both sides by 6
x = 36/6
x = 6
Therefore, the value of x from the perimeter of the triangle is 6
Read more on perimeter of triangle:
https://brainly.com/question/24382052
#SPJ1
When the function f(x) = 4(2)x is changed to f(x) = 4(2)x − 13, what is the effect? (5 points)
a
There is no change to the graph because the exponential portion of the function remains the same.
b
The x-intercept is 13 spaces higher.
c
The y-intercept is 13 spaces lower.
d
All input values are moved 13 spaces to the left.
Answers
Answer: C. The y-intercept is 13 spaces lower.
Step-by-step explanation:
A jet travels for 410 miles in 2 hours. at this rate how far could the jet fly in 14 hours? What is the rate of speed of the Jet
Answers
410/5 = ?
410/5 = 82
82 miles per hour
82*12 = ?
82*12 = 984
Answer: 984 miles in 12 hours
true or false? serving others can give you a break from focusing on your personal problems
Answers
Answer:
true
Step-by-step explanation:
Lincoln Middle School plans to collect more than 2,000 cans of food in a food drive. So far, 668 cans have been collected. Write and solve an inequality to find numbers of cans the school can collect on each of the final 7 days of the drive to meet this goal.Interpret the solution within the context of the problem. Describe your answer to the problem.

Answers
Let x be the number of cans of food, since we need more than or equal to 2000 cans, we can write
\(x+668\ge2000\)where 668 is the number of cans that they have been collected.
Now, we must find x. If we move 668 to the right hand side as -668, we get
\(\begin{gathered} x\ge2000-668 \\ \end{gathered}\)which gives
\(x\ge1332\)this means that they must collect more than or equalt to 1332 cans of food.
(2x+6y) exponent 2 with solution po thanks
Answers
Answer: (2x+6y)^2 = (2x+6y)(2x+6y) = 4x^2 +12xy + 12yx + 36y^2 = 4x^2 + 24xy + 36y^2
So the result of (2x+6y)^2 is 4x^2 + 24xy + 36y^2
From the ground floor to the second floor, there are 3 staircases, to the third floor there are also 3 staircases and each classroom has 2 doors. How many choices of passageways are there in entering the classroom?
a. 8
b. 9
c. 11
d. 18
Answers
The answer is d. 18. There are a total of 18 choices of passageways for entering the classroom.
To determine the number of choices of passageways, we need to consider the options at each step. From the ground floor to the second floor, there are 3 staircases, so we have 3 choices. From the second floor to the third floor, there are also 3 staircases, giving us another 3 choices. Now, for each classroom on the third floor, there are 2 doors, so we have 2 choices for each classroom. Since there are a total of 6 classrooms (assuming one classroom per staircase), we multiply the number of choices per classroom by the number of classrooms, which gives us 2 * 6 = 12 choices. Finally, we add up the choices from each step: 3 + 3 + 12 = 18. Therefore, there are 18 choices of passageways in entering the classroom.
Learn more about total here:
https://brainly.com/question/6506894
#SPJ11
Lance paid 6% sales tax on a $30 game. What is the total amount did Lance pay?
Answers
Answer:
The answer is attached.

27 is 50% of what number? Enter your answer in the space below.
Answers
Answer:
54
Step-by-step explanation:
so 27 is half of 54
I need help with this question?

Answers
Answer:
11⁹
Step-by-step explanation:
simplifying the question
Please help me this is hard and its due today!

Answers
Answer: A, C and E.
Step-by-step explanation: They all equal to 5.
Which expression is equivalent to 3^2x3^6? 9^12. 3^8. 3^12. 9^8
Answers
Answer:
3^8
Step-by-step explanation:
Please help me please

Answers
T/F: an example of a weight used in the calculation of a weighted index is quantity consumed in a base period.
Answers
False. The quantity consumed in a base period is not an example of a weight used in the calculation of a weighted index.
In the calculation of a weighted index, a weight is a factor used to assign relative importance or significance to different components or categories included in the index. These weights reflect the contribution of each component to the overall index value. The purpose of assigning weights is to ensure that the index accurately reflects the relative importance of the components or categories being measured.
An example of a weight used in a weighted index could be market value, where the weight is determined based on the market capitalization of each component. This means that components with higher market values will have a greater weight in the index calculation, reflecting their larger impact on the overall index value.
On the other hand, the quantity consumed in a base period is not typically used as a weight in a weighted index. Instead, it is often used as a reference point or benchmark for comparison. For example, in a price index, the quantity consumed in a base period is used as a constant quantity against which the current prices are compared to measure price changes.
Therefore, the statement that the quantity consumed in a base period is an example of a weight used in the calculation of a weighted index is false.
To learn more about weight, click here:
brainly.com/question/19053239
#SPJ1
for this lesson, you will come up with your own challenging algorithm for other students to trace. it must contain at least 4 if statements, 1 else statement and use at least one and or or boolean condition. note: elif statements will not count - your statements must be if statements. each if statement should use a unique variable name. for this challenge, try reading 3 or 4 of your classmates' code as well. trace their code and predict what it will output, then check the code by running it to see if you got it right, and submit your work for a grade.
Answers
By using Python, you will come up with your own challenging algorithm for other students to trace.
What are If else Statements ?If a certain is true, the if/else expression triggers a sequence of instructions to run. Another piece of code may be run if the condition is false.
The if/else statement is a component of Python's "Conditional" Statements, which are used to carry out various operations based on various circumstances.
These conditional statements are available in Python:
If you want a block of code to run only if a certain condition is true, use the if statement.
If the same expression is false, use instead that to provide a set of instructions that should be run.
If the first expression is false, can use else if sentence to establish a comprehensive criterion to test.
To choose which of the several program code should be performed, use the switch.
How to write the code?
num = 100
if num < 20:
print('Less than 20')
if num < 30:
print('Less than 30')
if num < 40:
print('Less than 40')
if num < 50:
print('Less than 50')
if num > 100 or num == 100:
print('More than or equal to 100')
To learn more abou If else statements, visit:
https://brainly.com/question/17140925
#SPJ4
Evaluate ∫∫∫ Q √y² +z²dV where Q is the solid region that lies inside the cylinder y² + z² =16 between the planes x = 0 and x = 3.
Answers
We are asked to evaluate the triple integral ∫∫∫ Q √(y² + z²) dV, where Q represents the solid region inside the cylinder y² + z² = 16 and between the planes x = 0 and x = 3.
To evaluate the given triple integral, we will use cylindrical coordinates. In cylindrical coordinates, we have x = x, y = r sinθ, and z = r cosθ, where r represents the radial distance, θ represents the angle in the yz-plane, and x represents the height.
First, we determine the limits of integration. Since the region lies inside the cylinder y² + z² = 16, the radial distance r ranges from 0 to 4. The angle θ can range from 0 to 2π to cover the entire yz-plane. For x, it ranges from 0 to 3 as specified by the planes.
Next, we need to convert the volume element dV from Cartesian coordinates to cylindrical coordinates. The volume element dV in Cartesian coordinates is dV = dx dy dz. Using the transformations dx = dx, dy = r dr dθ, and dz = r dr dθ, we can express dV in cylindrical coordinates as dV = r dx dr dθ.
Now, we set up the integral:
∫∫∫ Q √(y² + z²) dV = ∫₀³ ∫₀²π ∫₀⁴ r √(r² sin²θ + r² cos²θ) dx dr dθ
Simplifying the integrand, we have:
∫∫∫ Q r √(r²(sin²θ + cos²θ)) dx dr dθ
= ∫₀³ ∫₀²π ∫₀⁴ r² dx dr dθ
Evaluating the integral, we have:
∫∫∫ Q r² dx dr dθ = ∫₀³ ∫₀²π ∫₀⁴ r² dx dr dθ
Integrating over the given limits, we obtain the value of the integral.
To evaluate the integral ∫∫∫ Q √(y² + z²) dV, we converted it to cylindrical coordinates and obtained the integral ∫₀³ ∫₀²π ∫₀⁴ r² dx dr dθ. Evaluating this integral will yield the final result.
To learn more about integral click here : brainly.com/question/4746216
#SPJ11
participants in a study on the effects of viagra are assigned to groups. one group receives a sugar pill (a zero dose of viagra) while the other group receives viagra. the number of erections over 30 days is recorded by participants in a journal. in this example, what is the independent variable?
Answers
Participants in a study on the effects of viagra are assigned to groups, the independent variable is The viagra.
In an algebraic equation, an independent variable is a variable whose values are not impacted by changes. It is claimed that the value of y is a function of the value of the independent variable (x), also known as the x value, and the value of y is known as the dependent variable, in an algebraic equation with two variables (x and y), if any value of x is related to any other value of y.
The alphabetic letter that conveys a numerical value or a number is known as a variable in mathematics. In algebraic equations, a variable is used to represent an unknowable quantity.
For these variables, any alphabet from a to z may be used. Most frequently, the variables "a," "b," "c," "x," "y," and "z" are utilised in equations.
Learn more about Independent variable:
https://brainly.com/question/25223322
#SPJ4
Exhibit 6-3The weight of football players is normally distributed with a mean of 200 pounds and a standard deviation of 25 pounds.
Refer to Exhibit 6-3. The probability of a player weighing less than 250 pounds is _____.
Select one:
a. .9772
b. .0528
c. .4772
d. .5000
Answers
The probability of a player weighing less than 250 pounds is approximately 0.9772.
Answer: a. 0.9772
We can use the normal distribution to find the probability of a football player weighing less than 250 pounds.
First, we need to calculate the z-score of 250, using the formula:
\(z = (x - μ) / σ\)
where x is the weight of interest, μ is the mean weight, and σ is the standard deviation.
Plugging in the values, we get:
\(z = (250 - 200) / 25 = 2\)
Using a standard normal distribution table or calculator, we can find the probability that a standard normal random variable is less than 2. This probability is approximately 0.9772.
Since the weight of football players is normally distributed with mean 200 pounds and standard deviation 25 pounds, we can use the standard normal distribution to find the probability of a player weighing less than 250 pounds.
for such more questions on random variable
https://brainly.com/question/17217746
#SPJ11
The position of the front bumper of a test car under microprocessor control is given by x(t)=2.31m+(4.85m/s2)t2−(0.100m/s6)t6.(a) Find its position at the instants when the car has zero velocity.First instant x = _____ mSecond instant x = _____ mb) Find its acceleration at the instants when the car has zero velocity.First instant _____ m/s2second instant _____ m/s2
Answers
Step-by-step explanation:
(a) To find the position of the car when it has zero velocity, we need to find the times at which the velocity, x'(t), is equal to zero. The velocity of the car is given by:
x'(t) = (4.85m/s^2)t^2 - (0.100m/s^6)t^6
Setting x'(t) equal to zero and solving for t, we find:
0 = (4.85m/s^2)t^2 - (0.100m/s^6)t^6
t^2 = (0.100m/s^6)t^6 / (4.85m/s^2)
We can't solve for t analytically, but we can use numerical methods to find approximate values for the two times at which the velocity is equal to zero.
The first instant is approximately t = 0.68 s and the second instant is approximately t = 2.28 s.
Using these values for t, we can find the positions of the car at these instants:
x(0.68s) = 2.31m + (4.85m/s^2)(0.68s)^2 - (0.100m/s^6)(0.68s)^6
x(2.28s) = 2.31m + (4.85m/s^2)(2.28s)^2 - (0.100m/s^6)(2.28s)^6
(b) The acceleration of the car is given by the derivative of its velocity, x'(t):
x''(t) = 2(4.85m/s^2)t - 6(0.100m/s^6)t^5
Using the values of t from part (a), we can find the acceleration of the car at the instants when it has zero velocity:
x''(0.68s) = 2(4.85m/s^2)(0.68s) - 6(0.100m/s^6)(0.68s)^5
x''(2.28s) = 2(4.85m/s^2)(2.28s) - 6(0.100m/s^6)(2.28s)^5
a fair coin is flipped four times. findthe probability it will land up heads eachtime(b) the probability it will land the same way eachtime (slightly different from (a)).
Answers
The probability of getting heads each time is 1/16, and the probability of getting the same outcome (either heads or tails) each time is 1/8.
We know that the probability of getting a head or a tail when flipping a fair coin is 1/2. Let us use this fact to answer the given questions. The probability it will land the same way each time:
The probability of getting heads each time is (1/2) × (1/2) × (1/2) × (1/2) = 1/16.
The probability of getting tails each time is also 1/16.
Therefore, the probability of getting the same outcome (either heads or tails) each time is (1/16) + (1/16) = 1/8.
The probability of getting heads each time is lower than the probability of getting tails each time. This is because there are more ways to get tails each time than to get heads each time. For example, if we flip the coin four times, we can get heads-tails-heads-tails or tails-heads-tails-heads, but we cannot get heads-heads-heads-heads and tails-tails-tails-tails at the same time.
Therefore, the probability of getting heads each time is 1/16, and the probability of getting the same outcome (either heads or tails) each time is 1/8.
Learn more about probability visit:
brainly.com/question/31828911
#SPJ11
the _______ of 2 is 2A. signB. absolute value C. opposite
Answers
The sign | | is used to refer to the absolute value of an expression or integer.
Given an integer x
\(\begin{gathered} |x|=x \\ |-x|=x \end{gathered}\)The absolute sign will always return a positive value.
Therefore, the absolute value of 2 is 2.
The correct option is B.
show that the following functions are of exponential order • f(t) = t3 sin(t) • g(t) = t2et
Answers
Both f(t) and g(t) are of exponential order.
To show that a function f(t) is of exponential order, we need to find positive constants M and k such that:
|f(t)| <= M * e^(k*t) for all t >= t0, where t0 is some arbitrary constant.
Let's start by considering f(t) = t³ * sin(t). We can use the fact that |sin(t)| <= 1 to obtain an upper bound for f(t):
|f(t)| = |t³ * sin(t)| <= t³ for all t
Now we need to find k such that t³ <= M * e^(k*t) for all t >= t0. Taking logarithms of both sides yields:
ln(t³) <= ln(M * e^(kt)) = ln(M) + kt
Simplifying the left-hand side:
3 ln(t) <= ln(M) + k*t
Now we can choose M = 1 and k = 1 to obtain:
3 ln(t) <= ln(1) + t
3 ln(t) <= t
This inequality holds for all t >= 1, so we have shown that f(t) is of exponential order with M = 1 and k = 1.
Next, consider g(t) = t² * e^t. We can once again obtain an upper bound using the fact that e^t >= 1:
|g(t)| = |t² * e^t| <= t² * e^t for all t
To find M and k such that t² * e^t <= M * e^(k*t) for all t >= t0, we can again take logarithms of both sides:
ln(t² * e^t) <= ln(M * e^(kt)) = ln(M) + kt
Simplifying the left-hand side:
2 ln(t) + t <= ln(M) + k*t
Now we can choose M = 1 and k = 2 to obtain:
2 ln(t) + t <= ln(1) + 2t
2 ln(t) + t <= 2t
This inequality holds for all t >= 1, so we have shown that g(t) is of exponential order with M = 1 and k = 2.
Therefore, both f(t) and g(t) are of exponential order.
To know more about exponential order, refer to the link below:
https://brainly.com/question/30123751#
#SPJ11
graph the logarithmic function g(x)=log4(x-1)+2
Answers
See attachment for the graph of the function g(x)=log4(x-1)+2
How to graph the logarithmic function?The equation of the logarithmic function is given as
g(x)=log4(x-1)+2
The parent function of the above logarithmic function is
f(x) = log4(x)
This means that the parent function is translated right by 1 unit and translated up by 2 units
Next, we plot the graph of the function g(x)=log4(x-1)+2
See attachment for the graph of the function g(x)=log4(x-1)+2
Read more about logarithmic functions at:
https://brainly.com/question/13473114
#SPJ1

Find the domain and range of the function represented by the graph. Select all that apply.
What is the range

Answers
Answer:
Domain: [-2, 0, 2, 4]
Range: [3]
Step-by-step explanation:
The domain of the function are all values of x that are plotted on the horizontal axis (x-axis), while the range are the corresponding y-values plotted on the vertical axis (y-axis).
Therefore,
Domain of the function = [-2, 0, 2, 4]
Range of the function = [3] (only 1 possible value of y can be seen as plotted on the gray]
Which term for set A makes this diagram true? Choose true or false for each term.
Real Number
Rational numbers
A
A. Whole Numbers. True or False
B. Irrational Numbers. True or False
C. Integers. True or False
D. Repeating Decimals. True or False
Answers
B irrational numbers true or false