Find the value of 4x2 – 2y when x = 3 and y = 2.
Answers
Answer:20
Step-by-step explanation:
4(3)2-2(2)
12(2)-4
24-4=20
Related Questions
How do you find the area of a contour?
Answers
how many 0's are located to the right of the decimal point and before the first non-zero digit in the terminating decimal representation of $\frac{1}{2^5\cdot5^8}$?
Answers
There are 11 zeros in the given fraction's terminating decimal representation.
To determine the number of zeros to the right of the decimal point and before the first non-zero digit in the terminating decimal representation of \($\frac{1}{2^5\cdot5^8}$\) , we need to simplify the fraction.
\($\frac{1}{2^5\cdot5^8}$\) can be rewritten as \($\frac{1}{32\cdot390625}$\) .
To find the decimal representation of this fraction, we divide 1 by the product of the denominators: \($32\cdot390625$\) .
Performing the division, we get:
\($0.000000000000512$\)
In this decimal representation, there are 11 zeros located to the right of the decimal point and before the first non-zero digit, which is 5. Therefore, there are 11 zeros in the given fraction's terminating decimal representation.
To know more about decimal refer here:
https://brainly.com/question/30958821
#SPJ11
during the 2000 season, the home team won 138 of the 240 regular season national football league games. is this strong evidence of a home field advantage in professional football? test an appropriate hypothesis and state your conclusion. be sure the appropriate assumptions and conditions are satisfied before you proceed.
Answers
A) The 95% confidence interval is:
0.58 ± 0.062
B) At the 0.01 probability value, there is neither substantial evidence of a home-field advantage in professional football (they won and over half of the games).
Now, According to the question:
A) Confidence interval is written as
Sample proportion ± margin of error
Margin of error = z × \(\frac{\sqrt{pq} }{n}\)
Where:
z = The z score corresponds to the amount of confidence.
p = sample proportion.
q = probability of failure
q = 1 - p
p = x/n
Where
n = the number of samples
x = the number of success
From the information given,
n = 240
x = 138
p = 138/240 = 0.58
q = 1 - 0.58 = 0.42
To determine the z score, The confidence level from 100% to get α
α = 1 - 0.95 = 0.05
α/2 = 0.05/2 = 0.025
Thus,
1 - 0.025 = 0.975
The z -score associated with the area just on z table approximately 1.96. Therefore, the z score with a 95% confidence level is 1.96.
As a result, the 95% confidence interval becomes
0.58 ± 1.96√(0.58)(0.42)/240
Confidence interval is
0.58 ± 0.062
B) Earning more than half of the games equates to winning 120 games or more.
p = 120/240 = 0.5
The hypothesis test will be
For the null hypothesis,
P ≥ 0.5
For the alternative hypothesis,
P < 0.5
Probability of success, p = 0.5
q = probability of failure = 1 - p
q = 1 - 0.5 = 0.5
Considering the sample,
Sample proportion, P = x/n
Where
x = number of success = 138
n = number of samples = 240
P = 138/240 = 0.58
We need to find the values of the test statistic which will be the z score
z = (P - p)/√pq/n
z = (0.58 - 0.5)/√(0.5 × 0.5)/240 = 2.48
Remember that this is a two-tailed test. We would use the normal distribution table to calculate the probability potential of the property to the right of both the z score.
P value will be = 1 - 0.9934 = 0.0066
Since alpha, 0.01 > the p value, 0.0066, then we would reject the null hypothesis.
The given question is incomplete, The complete question is this:
__"During the 2000 season, the home team won 138 out of 240 regular season National Football League games. (15 points) a) Construct a 95% confidence interval for the winning proportion of the home team during this season. b) At the 0.01 significance level, is there strong evidence of a home field advantage (they win more than half of the games) in professional football? State hypotheses, calculate the test statistic and p-value, and make a conclusion in context"__
Learn more about Confidence Interval at:
https://brainly.com/question/29680703
#SPJ4
What is the answer to this?

Answers
What's the temperature? The temperature in a certain location was recorded each day for two months. The mean temperature was 76.4 ∘
F with a standard deviation 7.3 ∘
F. What can you determine about these data by using Chebyshev's Inequality with K=3 ? At least % of the days had temperatures between "F and
Answers
By using Chebyshev's Inequality with K=3, we can determine that at least 88.89% of the days had temperatures between "F and "F, where "F represents the mean temperature of 76.4°F.
Chebyshev's Inequality provides a lower bound on the proportion of data that falls within a certain number of standard deviations from the mean. In this case, K=3 means that we are considering a range of three standard deviations from the mean.
The inequality states that for any dataset, the proportion of data falling within K standard deviations of the mean is at least 1 - (1/K^2). So, for K=3, we have 1 - (1/3^2) = 1 - (1/9) = 8/9 ≈ 0.8889. Therefore, at least 88.89% of the data falls within three standard deviations of the mean.
In the context of the temperature data, we can conclude that at least 88.89% of the days had temperatures between the mean temperature of 76.4°F minus three standard deviations (76.4 - 3 * 7.3) and the mean temperature plus three standard deviations (76.4 + 3 * 7.3). This range represents a relatively high proportion of the dataset, indicating that the temperature observations are fairly concentrated around the mean with limited extreme values.
Learn more about standard deviations here:
brainly.com/question/13336998
#SPJ11
help plz !! Which is the graph of an even monomial function?
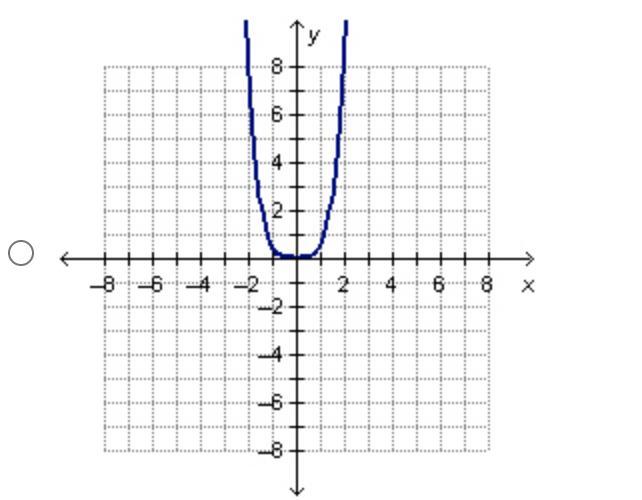



Answers
Answer:
Imagie 1 and 2
monomial function graph look like this
<3 ily
Red

Answer:
The first image
Explanation:
Hope you have a great day!
Suppose you received a score of 87 out of 100 on exam 1. The mean score for the exam was 79 and the standard deviation for the exam scores was 4. What score do you need on exam 2 to do equally well, if the mean score for exam 2 is 60 and the standard deviation for exam 2 is 6
Answers
You need a score of 72 out of 100 on exam 2 to perform as well as you did on exam 1.
To determine the score you need on exam 2 to perform as well as you did on exam 1, given the mean and standard deviation for exam 2 and the scores for exam 1, you can use the formula for z-scores.
The formula is :z = (X - μ) / σ,
where X is the score you received on exam 1, μ is the mean score for exam 1, and σ is the standard deviation for exam 1.
To find the score you need on exam 2, you can rearrange the formula as follows: X = z * σ + μ, where z is the z-score you calculated for your score on exam 1.
To calculate the z-score for your score on exam 1, you can use the formula: z = (X - μ) / σ = (87 - 79) / 4 = 2.T
o find the score you need on exam 2 to perform as well as you did on exam 1, you can substitute the values you have into the formula:
X = z * σ + μ = 2 * 6 + 60 = 72.
So, you need a score of 72 out of 100 on exam 2 to perform as well as you did on exam 1.
Know more about standard deviation here:
https://brainly.com/question/13498201
#SPJ11
Mrs. Larson, the science teacher, collected 18 sedimentary rocks and 12 metamorphic ones. Now she wants to create some identical kits for studying rocks, without having any rocks left over. What is the greatest number of kits she can create?
Answers
Answer:
The greatest number of kits she can create is 6 kits
Step-by-step explanation:
We can solve the above question using the greatest common factor method.
We have to find the factors of 18 and 12
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 18 are: 1, 2, 3, 6, 9, 18
Then the greatest common factor is 6.
Therefore, greatest number of kits that she can create is 6 kits
The number of sedimentary rocks in each kit
18 sedimentary rocks /6 kits = 3 sedimentary rocks
The number of Metamorphic rocks in each kit =
12 metamorphic ones/ 6 kits = 2 metamorphic rocks
12.6.3 Test (CST): Factoring Polynomials
According to the graph, what is the factorization of x² - 4x + 3?
O A. (x-3)(x + 1)
OB. (x+3)(x+1)
O C. (x-3)(x-1)
D. (x+3)(x - 1)

Answers
The factorization of the polynomial x² - 4x + 3 are (x - 1)(x - 3)
How to determine the factorization of x² - 4x + 3?From the question, we have the following parameters that can be used in our computation:
x² - 4x + 3
Also, we have the graph
From the graph, we can see that the graph intersects the x-axis ar
x = 1 and 3
This means that the factors are
(x - 1) * (x - 3)
So, we have
(x - 1)(x - 3)
Hence, the factorization of x² - 4x + 3 are (x - 1)(x - 3)
Read more about polynomial at
https://brainly.com/question/30833611
#SPJ1
An object is moving at a speed of 6 feet per day. Express this speed in miles per year. Round your answer to the nearest hundredth.
Answers
The speed of the object, which is moving at 6 feet per day, can be expressed as approximately 0.00114 miles per year. To calculate this, we convert the feet to miles and the days to years.
To convert feet to miles, we divide the distance in feet by the number of feet in a mile. Since there are 5,280 feet in a mile, we divide 6 feet by 5,280 feet/mile, which gives us 0.00113636 miles.
Next, we convert the speed from per day to per year. Since there are approximately 365.25 days in a year (accounting for leap years), we multiply the speed in miles per day by 365.25 days/year. Multiplying 0.00113636 miles/day by 365.25 days/year gives us 0.41475 miles/year.
Rounding this answer to the nearest hundredth, we get approximately 0.41 miles per year.
To learn more about speed click here: brainly.com/question/17661499
#SPJ11
If $10,000 is invested in an account earning 4.5% interest compounded continuously, determine how long it will take to money to grow to $15,000.
Answers
Therefore, it will take approximately 11.67 years for the money to grow from $10,000 to $15,000 at an annual interest rate of 4.5% compounded continuously.
To solve this problem, we can use the continuous compounding formula: A = Pe^(rt), where A is the final amount, P is the initial principal, e is Euler's number (approximately 2.71828), r is the annual interest rate as a decimal, and t is the time in years. We want to find t when A = $15,000 and P = $10,000. Plugging in these values and solving for t, we get:
$15,000 = $10,000e^(0.045t)
1.5 = e^(0.045t)
ln(1.5) = 0.045t
t = ln(1.5)/0.045
t ≈ 11.67 years
Therefore, it will take approximately 11.67 years for the money to grow from $10,000 to $15,000 at an annual interest rate of 4.5% compounded continuously.
To learn more about compound interest visit:
https://brainly.com/question/3989769
#SPJ11
Please I need help on a true or false

Answers
Answer:
True.
Explanation:
When solving equations with unknowns on both sides, it is generally recommended to first deal with the variable terms before dealing with the constant terms. This involves simplifying the equation by combining like terms and isolating the variable on one side of the equation. Once the variable is isolated, you can then solve for its value.\(\)
calculate the area, in square units, bounded above by x=−9−y−−−−√ 3 and x=−12y 6 and bounded below by the x-axis.
Answers
The area bounded above by the curves x = -9 - √(3y) and x = -12y and below by the x-axis is 24 square units.
What is the area enclosed by the curves x = -9 - √(3y) and x = -12y, with the x-axis as the lower boundary?The given problem asks us to calculate the area enclosed by two curves. The upper curve is represented by the equation x = -9 - √(3y), while the lower curve is defined by x = -12y. The region we are interested in lies below the x-axis. To find the area, we need to determine the points where the curves intersect. Setting the two equations equal to each other, we get -9 - √(3y) = -12y. By solving this equation, we find y = -1/3 and y = -3. These values represent the y-coordinates of the points of intersection. Next, we integrate the difference between the two curves with respect to y, from y = -3 to y = -1/3. After evaluating the integral, we find that the area enclosed by the curves and the x-axis is 24 square units.
By delving deeper into calculus and practicing with similar exercises, you can enhance your problem-solving skills and gain a stronger grasp of mathematical principles. Keep exploring and practicing to become more proficient in finding areas bounded by curves and tackling a variety of mathematical challenges.
Learn more about Curves
brainly.com/question/29408056
#SPJ11:
Slope of (1,-4) and (0,-5)
Answers
Answer:
Slope is 1
Step-by-step explanation:
use slope formula: m= \(\frac{y2-y1}{x2-x1}\)
m= \(\frac{-5+4}{0-1}\)
\(\frac{-1}{-1}=1\)
m=1
Hope this helps!
If not, I am sorry.
Hi student, let me help you out! :)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
We are asked to find the slope of
\(\star\mathrm{(1,-4)}\)
\(\star\mathrm{(0,-5)}\).
\(\triangle~\fbox{\bf{KEY:}}\)
Use the slope formula.Here's the slope formula:
\(\star\boxed{\mathrm{\cfrac{y2-y1}{x2-x1}}}\)
Input the values, which are:
y2=-5
y1=-4
x2=0
x1=1
\(\star\mathrm{\cfrac{-5-(-4)}{0-1}}\)
Simplify!
\(\star\mathrm{\cfrac{-5+4}{-1}}\)
\(\star\mathrm{\cfrac{-1}{-1}}\)
\(\star\boxed{\mathrm{1}}\)
Hope it helps you out! :D
Ask in comments if any queries arise.
#StudyWithBrainly
~Just a smiley person helping fellow students :)
\(\bf{\overline{\underline{\overline{\underline{Maribel\:Peri}}}}\)
Quetion 1
Janet drive at an average peed of 50 mile per hour to viit her grandparent, who live 200 mile away from Janet’ houe
Answers
Answer: ?
Step-by-step explanation: Is that the whole question? I don't really understand the question.
1Cm:15Km to the nearest 10000
Answers
The value of 1 cm : 1 km is 6.66666667e-7
How to evaluate the ratio?The ratio expression is given as:
1 cm : 15 km
Convert km to cm
So, we have
1 cm : 1 km = 1 cm : 1500000 cm
Express as quotient
1 cm : 1 km = 1 cm/1500000 cm
Evaluate the quotient
1 cm : 1 km = 6.66666667e-7
Hence, the value of 1 cm : 1 km is 6.66666667e-7
Read more about ratios at:
https://brainly.com/question/2328454
#SPJ1
If 58. 0 of hydrogen is heated to 140 degrees Celcius and expands to 90. 0 L, what was the original temperature?
_____ degree Celcius
(Precision to the nearest whole number)
Answers
To find the original temperature of the hydrogen, we need to use the ideal gas law, which states that the volume of a gas is directly proportional to its temperature (assuming that the pressure and the number of moles of gas remain constant).
The ideal gas law can be written as
V1/T1 = V2/T2,where V1 and T1 are the original volume and temperature of the gas, and V2 and T2 are the final volume and temperature of the gas.
In this case, we know that V1 = 58.0 L, V2 = 90.0 L, and T2 = 140 degrees Celsius. We can plug these values into the equation to find T1:
T1 = T2 * V1 / V2= 140 degrees Celsius * 58.0 L / 90.0 L
= 87.1 degrees Celsius
Rounding to the nearest whole number, we find that the original temperature of the hydrogen was 87 degrees Celsius.
Learn more about Ideal Gas Law here:
https://brainly.com/question/25290815
#SPJ4
simplify:
4 x - -5х + 3x- x+2х - 7х
Answers
Answer:
6x
Step-by-step explanation:
4 x - -5х + 3x- x+2х - 7х
Combine like terms so, so since all are the same you just do the operation they want u to do..
4x + 5x= 9x
9x + 3x = 12x
12x - x = 11x
11x + 2x= 13x
13x - 7x = 6x
Hint: 2 negatives make a postitive
Hint: in there is just an "x" there is always an invisible one in it... 1x
Hope this helped!
Olivia prepared 30 kilograms of dough after working 6 hours. How much dough did Olivia prepare if she worked for 10 hours? Solve using unit rates.
Answers
Answer:
50 kg
Step-by-step explanation:
6/30 = 5 which means she makes 5 kg every hour
so with the given information you multiply 5 and 10 and that's how you get 50
i hope this helps! :)
Find the midline of the graph of the function
g(x) = cos (3x)
A) x = 0
B y = 3
C y = 0
D none
Answers
What is the value of the rational expression 2x2+ 5x +9/x2+2x -1?
A.)-7
B.)-9
C.)9
D.)7
(Help Please.)
Answers
Answer:
hai
Step-by-step explanation:
what is the volume of the sphere shown below with a radius of 9
Answers
Answer:
972π or 3052.08 if π=3.14(remember to label the answer with your units)
Step-by-step explanation:
The formula for the volume of a sphere is \(\frac{4}{3}\\\)π\(r^{3}\). So, just plug the radius into the formula. \(r^{3}\) in this case is \(9^{3}\) which is 729. For, \(\frac{4}{3}\)×729, the 3 and 729 cancel out to create 4×243 which is 972. Just add π to this and you get 972π. If π is 3.14 just multiple 972 and 3.14 to get 3052.08.
ANSWER FAST PLZ .............

Answers
Answer:
a) T
B) WT and TZ
C) ZTU
D) YTX
E) YT and WT
F) Angle 5 - right angle
G) obtuse angle (>90)
H) acute angle (<90)
I) obtuse angle, unless it means the other side which would be a reflex angle instead (>180)
Hope this helped!
Find the solution to the unforced ODE given with initial conditions y(0)=2 and y (0)=8. 2 y (t)+8 y(t)−10y(t)=0
Answers
The solution to the given unforced ODE with initial conditions y(0) = 2 and y'(0) = 8 is y(t) = 4e-2t + 2e-4t.
To obtain this solution, we start by solving the ODE:
2y (t) + 8y' (t) − 10y(t) = 0
The characteristic equation for this ODE is r2 + 8r − 10 = 0, which has solutions r = -2 and r = -4. This gives us the general solution of the ODE as:
y(t) = A e-2t + B e-4t.
Using the initial conditions given, we can determine the values of A and B:
y(0) = 2 = A + B
y'(0) = 8 = -2A + -4B
By solving the system of equations, we obtain A = 2 and B = 2. Therefore, the solution to the given ODE is y(t) = 4e-2t + 2e-4t.
To know more about Equation click here:
https://brainly.com/question/29657983#
#SPJ11
Can anyone help me out on this

Answers
Answer:
hkfgyjfjyfj685
Step-by-step explanation:
rdytesrghd
Is negative 1 a real number?
Answers
Write the equation of a line through (2, -3), perpendicular to y = 1/3x
Answers
to make a perpendicular function from another we must take its slope and make two transformations
the slope of y=1/3x is 1/3
the transformations:
1.
reverse the number
\(\frac{1}{3}\longrightarrow\frac{3}{1}=3\)2.
and change the sign
\(3\longrightarrow-3\)ok we have the slope now need the general equation of the line
\(y=mx+b\)where m is the slope , b a cut point and (x,y) a point
so, we have the slope=-3 , and the point (2,-3) we can replace to find b
\(\begin{gathered} (-3)=(-3)(2)+b \\ -3=-6+b \\ b=-3+6 \\ b=3 \end{gathered}\)now we can replace b and the slope to have the final equation
\(y=-3x+3\)Write the missing partial products in the area model Then, write the partial to complete the equation below. Find the sum

Answers
The missing partial products are:
10 x 2 = 20
6 x 50 = 300
6 x 2 = 12
The sum of the partial products is,
16 x 52 = 500 + 300 + 20 + 12 = 832
Here the partial products method is used to find the product of two two digit numbers 16 and 52.
For this a table of the form given in the figure is constructed in which the partial products are found.
For this first split 16 and 52 into 10 + 6 = 16 and 50 + 2 = 52.
Then take the partial products between 10 and 50, 10 and 2, 6 and 50, 6 and 2. Then take the sum of all these four values to get the final answer. This is the method of partial products.
So finding the partial products,
10 x 50 = 500
10 x 2 = 20
6 x 50 = 300
6 x 2 = 12
To find the final answer, take the sum of these products.
500 + 300 + 20 + 12 = 832
⇒ 16 x 52 = 832
Learn more about partial products at https://brainly.com/question/24716925
#SPJ1
6-8 weeks i hope this help:)
Answers
Answer:
I have no idea but okay
The sum of the ages of Noi's and Noy's is 26 years. The different between four times Noi's age and two times Noy's age is 28 years. Find the age of Noi and Noy.
WRITE AS AN EQUATION
Answers
Answer:
The age of Noi is 13.333 Years and the age of Noy is 12.67 years
Step-by-step explanation:
The given information are;
The sum of the ages of Noi and Noy = 26 years
Four times Noi's age - Two times Noy's age = 28
Let the age of Noi = X and let the age of Noy = Y
We have;
X + Y = 26 years.................(1)
4X - 2Y = 28 years.............(2)
Divide equation (2) by 2 to get;
(4X - 2Y)/2 = (28 years)/2 which gives;
2X - Y = 14 years.................(3)
Add equation (3) to equation (1), to get;
X + Y + 2X - Y = 26 years + 14 years
3X = 40 years
X = 40/3 = 13.333 Years
From equation (1), X + Y = 26 years, therefore;
Y = 26 - X = 26 - 13.33 = 12.67 years
Therefore, the age of Noi = 13.333 Years and the age of Noy = 12.67 years.