Answers
The answer is c
Find the area of the triangle to get 72cm^2. There are two triangles so times 72 by 2 to get 144
Find the area of the first side by doing 12 x 30 = 360cm^2
Find the area of the second side by doing 9 x 30 = 270cm^2
Find the area of the base by doing 18 x 30 = 540cm^2
Add 144+360+270+540 = 1314cm^2
Related Questions
There are three plants that manufacture the boots, two distribution centers, and five warehouses. We need to ship the boots to the warehouses at a minimum cost satisfying the constraints outlined in the spreadsheet. Namely, each plant can only produce so much product, the amount of boots passing through the distribution centers has to remain constant
Answers
The problem can be modeled as a linear programming problem. We need to minimize the total cost of shipping the boots, which can be represented as a linear combination of the shipment quantities.
Thus, the objective function to be minimized can be written as:
Minimize Z = 4x11 + 5x12 + 7x13 + 6
32 + y33 ≤ 40 (capacity limit at warehouse 3)
y41 + y42 + y43 ≤ 30 (capacity limit at warehouse 4)
y51 + y52 + y53 ≤ 45 (capacity limit at warehouse 5)
xij, yjk ≥ 0 (non-negativity constraint)
Thus, the complete linear programming problem can be formulated as:
Minimize Z = 4x11 + 5x12 + 7x13 + 6x21 + 4x22 + 5x23 + 4y11 + 3y12 + 6y13 + 5y21 + 5y22 + 4y23 + 6y31 + 7y32 + 5y33 + 4y41 + 6y42 + 5y43 + 5y51 + 4y52 + 6y53
Subject to:
x11 + x12 + x13 ≤ 60
x21 + x22 + x23 ≤ 90
x11 + x21 = y11 + y21 + y31 + y41 + y51
x12 + x22 = y12 + y22 + y32 + y42 + y52
x13 + x23 = y13 + y23 + y33 + y43 + y53
y11 + y12 + y13 ≤ 35
y21 + y22 + y23 ≤ 50
y31 + y32 + y33 ≤ 40
y41 + y42 + y43 ≤ 30
y51 + y52 + y53 ≤ 45
xij, yjk ≥ 0
Solving this linear programming problem using a suitable solver will provide us with the optimal values of xij and yjk, which will help us in determining the minimum cost required for shipping the boots while satisfying all the constraints.
To know more about linear programming problem:
https://brainly.com/question/30074109
#SPJ4
Is 4.887888 a rational number
Answers
Answer:
Step-by-step explanation:
yes it is
Solve by the substitution method. 7x+8y=10 -3x+y=9
Answers
Answer:
Point form: (-2,3)
Equation form: x= -2, y=3
Step-by-step explanation:
Hope it helps!
The cost of 2kg apples and 3 kg oranges is Rs. 120. [Take x and y as the cost per kg of apples and oranges respectively.]
Answers
Step-by-step explanation:
2+3=120
5=120
=120
5
=24
apple=2 multiply 24 is 48
orange=3 multiply 24 is 72
A square pyramid has a base with sides of length x inches and a height of 6 inches. which expression
represents the volume of the pyramid in cubic inches?
Answers
Answer:
length • width = area
expression:
area • height = (result) • 1/3 = volume
Example:
x (area) • 6 (height) = 6x
6x • 1/3 = 2x(inches)³ or 6x ÷ 3 = 2x(inches)³
PLEASE HELP ME ASAP PLEASE.

Answers
Answer:
See below
Step-by-step explanation:
g (h(6)) :
h (6) = 3 ( 6^2) + 2 = 110
then g (110) = sqrt (110)
h (g(5))
g(5) = sqrt 5
then h( sqrt5) = 3 ( sqrt5)^2 + 2 = 17
what's 182.91% as a decimal
Answers
Answer:
1.8291
Step-by-step explanation:
41. fanciful shapes can be created by using the implicit plotting capabilities of computer algebra systems.
(d) create even more fanciful curves by modifying the equation in part (a).
Answers
Modifications are just a starting point, and you can explore endless possibilities by experimenting with different mathematical functions, operations, and parameters.
To create even more fanciful curves, you can modify the equation from part (a) by introducing additional terms or manipulating the existing terms. Here are a few examples of modifications you can make to create interesting shapes:
Adding or multiplying terms: You can introduce additional terms to the equation, such as adding or multiplying variables or constants. For example, if the original equation was y = x², you can modify it to y = x³ + 2x² + x, which would create a more intricate curve with higher-order terms.
Trigonometric functions: You can incorporate trigonometric functions like sine, cosine, or tangent into the equation. This can produce curves with periodic patterns or wave-like shapes. For instance, modifying the equation y = x² to y = x² + sin(x) would introduce oscillations to the curve.
Exponential functions: Exponential functions can also be used to create interesting curves. By including terms like eˣ or e⁻ˣ, you can achieve curves that grow or decay exponentially. Modifying the equation y = x²to y = x² + e⁻ˣ would create a curve that decreases exponentially as x increases.
Combining functions: You can combine multiple functions using addition, subtraction, multiplication, or composition to generate complex shapes. For example, y = sin(x)× cos(2x) would result in a curve that exhibits both sine and cosine patterns simultaneously.
Parameterization: Introducing parameters into the equation allows you to control various aspects of the curve, such as its shape, size, or position. By adjusting these parameters, you can create a wide range of fanciful curves. For example, in the equation y = a× x², you can vary the value of 'a' to stretch or compress the parabola.
Remember, these modifications are just a starting point, and you can explore endless possibilities by experimenting with different mathematical functions, operations, and parameters. Computer algebra systems can help you visualize the resulting curves and explore their properties in detail.
Learn more about exponential function here:
https://brainly.com/question/28596571
#SPJ11
The area of a rectangular wall of a barn is 252 square feet. Its length is 10 feet longer than twice its width. Find the length and width of the wall of the barn.
Answers
Answer: Length = 28 feet and width = 9 feet
Step-by-step explanation:
Let x = width of the wall.
Then, Length of the wall = 10+2x
Since , Area of rectangle = length x width
Then, as per given,
\(252= (10+2x)x\\\\\Rightarrow\ 252=10x+2x^2\\\\\Rightarrow\ 2x^2+10x-252=0\\\\\Rightarrow\ x^2+5x-126=0\\\\\Rightarrow\ x^2+14x-9x-126=0\\\\\Rightarrow\ (x+14)-9(x+14)=0\\\\\Rightarrow\ (x+14)(x-9)=0\\\\\Rightarrow\ x=-14 \ or \ x= 9\)
Since width cannot be negative , so x = 9
So width = 9 feet and length = 10+2(9)=10+18 = 28 feet
Hence, length is 28 feet and width is 9 feet of the wall of the barn.
Which expression is equivalent to 4/9(2n – 3)?
Answers
Answer:
8/9n - 1 1/3
Step-by-step explanation:
find the value of 'x' in each of the following figures.

Answers
Answer:
You Have to Find Answer Yourself
Step-by-step explanation:
By This - B+D+C = 130°-20°+E
Answer:
110 degrees
Step-by-step explanation:
when continuing line DC down to line AE, it creates a triangle with the intersection point at AE, C and E.
the angles in that triangle are
E (20 degrees)
the internal angle at C = 180 - 130 = 50 degrees
and the angle at the interception point at AE.
since CD is parallel to AB, that angle is equal to x.
the sum of all angles in a triangle is airways 180 degrees.
therefore this angle is
180 - 20 - 50 = 110 degrees = x
f(x) = 17 - 2x
Find f(a + 7)
Answers
Answer:
-2a + 3
Step-by-step explanation:
We can substitute a + 7 for x:
f(a + 7) = 17 - 2(a+7) = 17 - 2a - 14 = -2a + 3
a characteristic, usually a numerical value, which describes a sample is called a _______. a. parameter b. statistic C. constant d. variable
Answers
Answer: B. statistic
Step-by-step explanation: A characteristic, usually a numerical value, which describes a sample, is called a statistic.
Unit 2 logic and proof homework 3 conditional statements
Answers
By engaging in these exercises, students can develop a deeper understanding of conditional statements and logical reasoning, which are essential skills for further studies in mathematics and logic.
In Unit 2 of a logic and proof course, homework 3 focuses on conditional statements.
Conditional statements are fundamental concepts in logic and mathematics, representing logical implications between two statements.
They are typically expressed in "if-then" format, where the "if" part is the hypothesis and the "then" part is the conclusion.
The homework may involve tasks such as:
Identifying conditional statements: Students are given a set of statements and asked to identify which ones are conditional statements.
They need to recognize the "if-then" structure and correctly identify the hypothesis and conclusion.
Analyzing the truth value of conditional statements:
Students may be given conditional statements and asked to determine whether they are true or false.
They need to evaluate the hypothesis and conclusion to determine if the implication holds in each case.
Writing converse, inverse, and contrapositive statements:
Students may be required to manipulate given conditional statements to form their converse, inverse, and contrapositive statements.
This involves switching the positions of the hypothesis and conclusion or negating both parts.
Applying the laws of logic:
Students may need to apply logical laws, such as the Law of Detachment or the Law of Modus Tollens, to deduce conclusions based on conditional statements.
Constructing counterexamples:
Students may be asked to provide counterexamples to disprove statements that are falsely claimed to be universally true based on a given conditional statement.
They also help students develop critical thinking and problem-solving abilities, as they have to analyze and manipulate logical structures.
For similar questions on conditional
https://brainly.com/question/27839142
#SPJ8
Juan is a tennis player who has won 52% of his tennis matches.
What is the probability that he will lose his next tennis match?
48%
2%
52%
50%
Answers
The probability that Juan loses his next tennis match is 48%
How to determine the probability that he will lose his next tennis match?From the question, we have the following parameters
The proportion of tennis matches won
p = 52%
This proportion implies that the probability that the player will win his next tennis match
So, we have the following representations
Probability of winning, p = 52%
Express the percentage as decimal
So, we have the following representations
Probability of winning, p = 0.52
The probability of losing the next match is the complement of the probability of winning
This is represented as
Probability of losing = 1 - Probability of winning,
Substitute the known values in the above equation
So, we have the following equation
Probability of losing = 1 - 0.52
Evaluate
Probability of losing = 0.48
Hence, the probability is 0.48 or 48%
Read more about probability at
https://brainly.com/question/251701
#SPJ1
Can someone help me with this question?

Answers
Answer:
radius, center, chord, diameter
Step-by-step explanation:
a. radius
b. center
c. chord
d. diameter
It takes your equipment 3 minutes to travel 264 feet. what speed is the equipment traveling?
Answers
Answer:
To determine the speed, we can use the formula:
speed = distance / time
where distance is measured in feet and time is measured in minutes.
In this case, the distance is 264 feet and the time is 3 minutes. Plugging these values into the formula, we get:
speed = 264 feet / 3 minutes
simplifying, we get:
speed = 88 feet/minute
Therefore, the equipment is traveling at a speed of 88 feet per minute.
There are 90 seats in the school auditorium. The school had a sold out show of their play last
weekend, and made $315. The cost of a ticket for an adult was $5.00 and the cost of a ticket for a child is $2.50. Which system of equations could be used to determine the number of adults, a, and
the number of children, c, that attended the showing of the movie?
Answers
Answer:
63 seat for adults and 27 seat for children.
please mark me as brainliest
(C) Suppose G Is A Function Continuous At A And G(A)>0. Prove That There Exists A Positive Constant C Such That G(X)>C For All X
Answers
We can prove that there exists a positive constant C such that G(x) > C for all x, where G is a continuous function.
G is a function continuous at a and G(a)>0.
We have to prove that there exists a positive constant C such that G(x)>C for all x.
To prove this statement, we can use the epsilon-delta definition of continuity.
According to the epsilon-delta definition of continuity, if G is continuous at a, then for every ε > 0 there exists a δ > 0 such that for all x with |x - a| < δ, we have |G(x) - G(a)| < ε.
Now since G(a) > 0, let ε = G(a)/2.
So there exists a δ > 0 such that for all x with |x - a| < δ,
we have |G(x) - G(a)| < G(a)/2.
Since G(a) > 0,
we can multiply both sides of this inequality by 2 to get:
2|G(x) - G(a)| < G(a).
Adding G(a) to both sides, we get:
2|G(x) - G(a)| + G(a) < 2G(a).
Let C = G(a)/2.
Then we have:
|G(x) - G(a)| < C for all x with |x - a| < δ.
G(x) - G(a) > -C and G(x) - G(a) < C.
Then G(x) > G(a) - C > 0 for all x with |x - a| < δ, so we can choose δ small enough that |x - a| < δ implies G(x) > G(a) - C > 0.
Thus we have proved that there exists a positive constant C such that G(x) > C for all x.
To know more about epsilon-delta definition of continuity, visit:
https://brainly.com/question/32104905
#SPJ11
Fine the UNIT RATE: 8 apples for $3
You can't do that, it doesn't divide out evenly
A..38
B..375
C.2.6666.......
D.2.67
Answers
Answer:
d
Step-by-step explanation:
8/3
The volume of this cone is 643,072 cubic inches. What is the radius of this cone?
Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
The radius of the cone is 783.84/√h
What is volume of a cone?A cone is the surface traced by a moving straight line (the generatrix) that always passes through a fixed point (the vertex).
Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
The volume of a cone is expressed as;
V = 1/3πr²h
643072 × 3 = 3.14 × r²h
r²h = 614400
r² = 614400/h
r = 783.84/√h
therefore the radius of the cone is 783.84/√h
learn more about volume of cone from
https://brainly.com/question/1082469
#SPJ1
Help me with this worksheet please give me he answer!
I'm in a hurry!


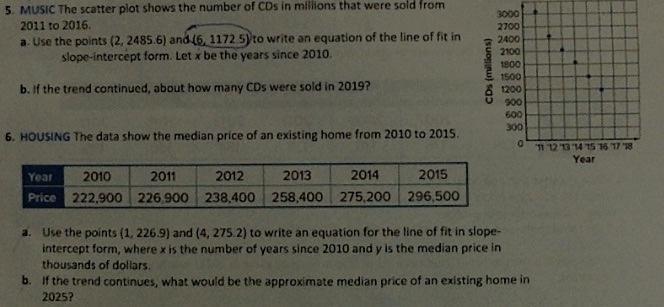
Answers
The approximate annual cost of raising a child born in 2013 at age 17 is 15230.
What is scatter plot?Scatter plots are used to observe and plot relationships between two numeric variables graphically with the help of dots. The dots in a scatter plot shows the values of individual data points.
a) Plot (2, 12,940), (5, 12,970), (8, 12,800), (11, 13,600) 1nd (14, 14420) on graph.
b) (8, 12800) and (14, 14420)
Here, slope m=(14420-12800)/(14-8)
= 1,620/6
= 270
Substitute m=270 and (x, y)=(8, 12800) in y=mx+c, we get
12800=270(8)+c
12800=2160+c
c=10640
Substitute m=270 and c=10640 in y=mx+c, we get
y=270x+10640
c) Now, substitute x=17 in y=270x+10640, we get
y=270×17+10640
y=15230
Therefore, the approximate annual cost of raising a child born in 2013 at age 17 is 15230.
To learn more about the scatter plot visit:
https://brainly.com/question/29231735.
#SPJ1
The largest numbers that can be divided by (without a remainder) both the numbers being compared (can be 1, can't be bigger than either number) is called the ______.
Answers
Answer:
GCF, Greatest Common Factor
Step-by-step explanation:
Hope this helped
The cost of each ticket at the carnival was $0.25. Li bought $7.50 worth of tickets. How many tickets did she buy?
help me please
Answers
A person places 1 penny in a piggy banking the first day of the month,
Answers
Answer: What’s the rest of the question?
Step-by-step explanation:
the truncation error from one step to step another, also called local truncation error, in a runge-kutta method is given to you as of o(h3). the global truncation error in the runge-kutta method then is of o(hn).the value of n is .
Answers
In a Runge-Kutta method, the local truncation error measures the error made in one step of the method, while the global truncation error measures the cumulative error over all the steps.
Given that the local truncation error of the Runge-Kutta method is of O(h^3), we can express the local error as:
LTE = C1 h^3 + C2 h^4 + ...
where C1, C2, ... are constants.
To obtain the global truncation error, we need to sum the local truncation errors over all the steps. Suppose we take n steps, each of size h. Then, the total error is of the form:
GTE = C1 h^3 + C2 h^4 + ... + Cn h^(n+2)
where the powers of h increase as we take more steps.
Since the global truncation error is also of O(h^n), we can equate the highest power of h in the above equation to n:
n + 2 = n
Solving for n, we get:
n = 2
Therefore, the value of n is 2.
To know more about Runge-Kutta method,
https://brainly.com/question/31854918
#SPJ11
In testing for differences between the means of 2 independent populations the null hypothesis is?
Answers
In testing for differences between the means of 2 independent populations the null hypothesis is zero.
What is Null hypothesis?This is defined as a statistical hypothesis which has no statistical significance in a set of given observations.
In testing for differences between the means of 2 independent populations the null hypothesis is the difference between the two population means and is not significantly different from zero which is denoted below:
H₀: µ₁ - µ₂ = 0
Read more about Null hypothesis here https://brainly.com/question/15980493
#SPJ4
Tamara caught a fish that weighs 5.6 pounds. Victoria
caught a fish that weighs 3.4 pounds. What is the
difference between the weights of the fish?
Answers
Answer:
2.2 pounds
Step-by-step explanation:
Your welcome
5.6
-3.4
———
2.2
Identify the like terms in the expression.

Answers
Answer:D
The answer is D.
Step-by-step explanation:
Like terms are only related to the variable at the end, and the variable also has to have the same exponent or it is not a like term.
A pasture is 1500 feet by 2000 ft. If a fence is to be built on this property, how many acres are
being fenced? If a role of woven wire is 330 ft long. How many rolls of fencing needs to be
purchased if you are also adding 2 drive through gates (16 ft each) and 4 walk through gates (4 ft
each).
Answers
The pasture is 68.73 acres. Total fence length: 7000 ft + 32 ft (drive-through gates) + 16 ft (walk-through gates). You need approximately 22 rolls of woven wire fencing.
To find the area of the pasture in acres, we need to convert the given measurements from feet to acres.
1 acre = 43,560 square feet
Area of the pasture = 1500 ft * 2000 ft = 3,000,000 square feet
Area in acres = 3,000,000 square feet / 43,560 square feet per acre ≈ 68.73 acres
So, the area being fenced is approximately 68.73 acres.
Now, let's calculate the total length of fencing required, taking into account the gates.
Length of fence needed = perimeter of the pasture + length of drive-through gates + length of walk-through gates
Perimeter of the pasture = 2 * (length + width)
Perimeter = 2 * (1500 ft + 2000 ft) = 2 * 3500 ft = 7000 ft
Length of drive-through gates = 2 * 16 ft = 32 ft
Length of walk-through gates = 4 * 4 ft = 16 ft
Total length of fencing needed = 7000 ft + 32 ft + 16 ft = 7048 ft
Now, we can calculate the number of rolls of woven wire fencing needed.
Length of one roll of woven wire = 330 ft
Number of rolls needed = Total length of fencing needed / Length of one roll of woven wire
Number of rolls needed = 7048 ft / 330 ft ≈ 21.39 rolls
Since we can't purchase a fraction of a roll, we'll need to round up to the nearest whole number.
Therefore, you would need to purchase approximately 22 rolls of woven wire fencing.
To learn more about perimeter click here
brainly.com/question/30252651
#SPJ11
