find the solution to the following system substitution y=-2 x -3 y= 3 x + 12
Answers
The solution to the system substitution is (x , y) = (-3,3).
What is substitution?The substitution operation in algebra is used to systematically replace instances of a symbol with a given value in various settings involving formal objects containing symbols (commonly called variables or indeterminates).A fundamental operation in computer algebra is substitution.In computer algebra systems, it is frequently abbreviated as "subs" or "subst."Here it is given that,
y=-2 x -3 and y= 3 x + 12
Take y=-2 x -3 as equation 1,
y= 3 x + 12 as equation 2'
by equating both equations,
-2x-3=3x+12
-3-12=3x+2x
5x=-15
x=-15/5
=-3
substituting the value of x in the equation1
y=-2x-3
y=-2(-3)-3
=3
Hence, The solution to the system substitution is (x , y) = (-3,3).
To learn more about substitution refer to:
https://brainly.com/question/22340165
#SPJ1
Related Questions
<
:
Introduction - Surface Area of Composite Figures
Peacing
Acellus
Find the surface area of the composite figure.
ch
5
3 in.
11 in.
3 in.
3 in.
Help Resources
6 in
6 in.
11 in.
8 in.
SA
[?] in.2
If you'd like
you can use a
calculator
Enter
Copyright © 2003-2022 International Academy of Science. All Rights Reserved.

Answers
The surface area of the figure is:
3 × 11 × 2 + 3 × 3 × 2 + 6 × 8 × 2 + 11 × 6 × 2 + 8 × 11 × 2
= 66 + 18 + 96 + 132 + 176
= 488in² (addition)
(Please give me positive feedback!! Thank you <3)
THE TOPIC IS: AREA OF CIRCLES!! PLEASE HELP ME WITH THIS QUESTION!!! WHATS THE ANSWER?? I WILL GIVE YOU BRAINLIEST AND A THANKS!!! AND PLS PUT AN EXPLANATION!! THANK YOU

Answers
Answer:
Step-by-step explanation:
6) diameter = 2 cm
Radius is half of diameter
r = 2 /2 = 1 cm
Area of circle = πr² {Plugin r = 1 in the formula}
= π*1²
= π cm²
7) r = 7.4 cm
Area = πr²
= π * 7.4*7.4
= 54.76π cm²
a
An aircraft has just taken off from an airport, the
Formula for it heights above the ground (hm) after it has
travelled d m horizontally is h= 3/8(d-480), make d the subject of the formala.
Use your result to find d when h= 500m.
Answers
The value of d when h is 500m is approximately 1,813m
How to find the height of the aircraftGive the heights above the ground (hm) after it has dropped expressed as:
h = 3/8(d-480),
If h = 500m, then;
500 = 3/8(d - 480)
Cross multiply
500*8 = 3(d - 480)
4000 = 3(d - 480)
Expand to have:
4000 = 3d - 1440
3d = 5440
d = 1,813.3m
Hence the value of d when h is 500m is approximately 1,813m
Learn more on functions and values here: https://brainly.com/question/2284360
What is the factorization of the trinominal below? x^2-2x-24

Answers
We have correctly factorized the trinomial x^2 - 2x - 24 into the product of two binomials: (x - 6)(x + 4).
Factorization is the process of finding the factors of an expression. This is an important tool in algebra, as it allows us to simplify expressions and solve equations more easily. In this question, we are asked to factorize the trinomial x^2 - 2x - 24.
The first step in factorizing a trinomial is to look for a common factor that can be taken out. In this case, we can see that the coefficients of x^2 and x are both 1, so there is no common factor to take out.
Next, we need to look for a pair of numbers that multiply to give the constant term (-24) and add up to give the coefficient of x (-2). To do this, we can list the factors of -24 and try to find a pair that adds up to -2.
The factors of -24 are: 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 8, -8, 12, and -12. We can quickly see that the only pair of factors that add up to -2 are -4 and 6.
So we can write: x^2 - 2x - 24 = (x - 6)(x + 4)
This is the factorization of the given trinomial. We can check that it is correct by using the distributive property:
(x - 6)(x + 4) = x(x + 4) - 6(x + 4) = x^2 + 4x - 6x - 24 = x^2 - 2x - 24
Therefore, we have correctly factorized the trinomial x^2 - 2x - 24 into the product of two binomials: (x - 6)(x + 4).
For more such questions on trinomial
https://brainly.com/question/29827487
#SPJ8
Find the value of x. Round to the nearest tenth

Answers
Answer:
x ≈ 21.7
Step-by-step explanation:
The relevant trig relation is ...
Cos = Adjacent/Hypotenuse
cos(37°) = 17.3/x
x = 17.3/cos(37°)
x ≈ 21.7
What two numbers multiply to -25 adds up to 2
Answers
Solve the system by substitution.
-5x+3y=2
Y=2x
Answers
Answer:
2 is the required answer.
Step-by-step explanation:
Solution:
Given:
-5x+3y=2..............(i)
Putting the value of y=2x in the equation (i); we get:
i.e -5x+3×2x=2
or, -5x+6x=2
or, x=2
i.e. x=2
y=2x=2×2=4
Gabriel made 6 small meatloaves. He cut each meatloaf into fourths.
How many
1
4
-size pieces of meatloaf does Gabriel have? please respond this message will be due till sunday
Answers
Answer:
24 1/4 sized pieces
Step-by-step explanation:
If there are 4 pieces in each loaf just multiply by 6 and you got your answer.
Need help with this problem it’s edg 2020

Answers
Because the orange lie is on 7.
i need help with the equation (11) - 2.
Answers
Answer:
it's technically 9 because it's the same as 11-2
544 rounded to the nearest ten
Answers
Answer:
544 rounded to the nearest 10 is 540
Step-by-step explanation:
541-544 is under 5 which is half way so then you do = 540
But if 545-549 then you do 550
hope this helps
Need help on this question pls help!!!!!!!
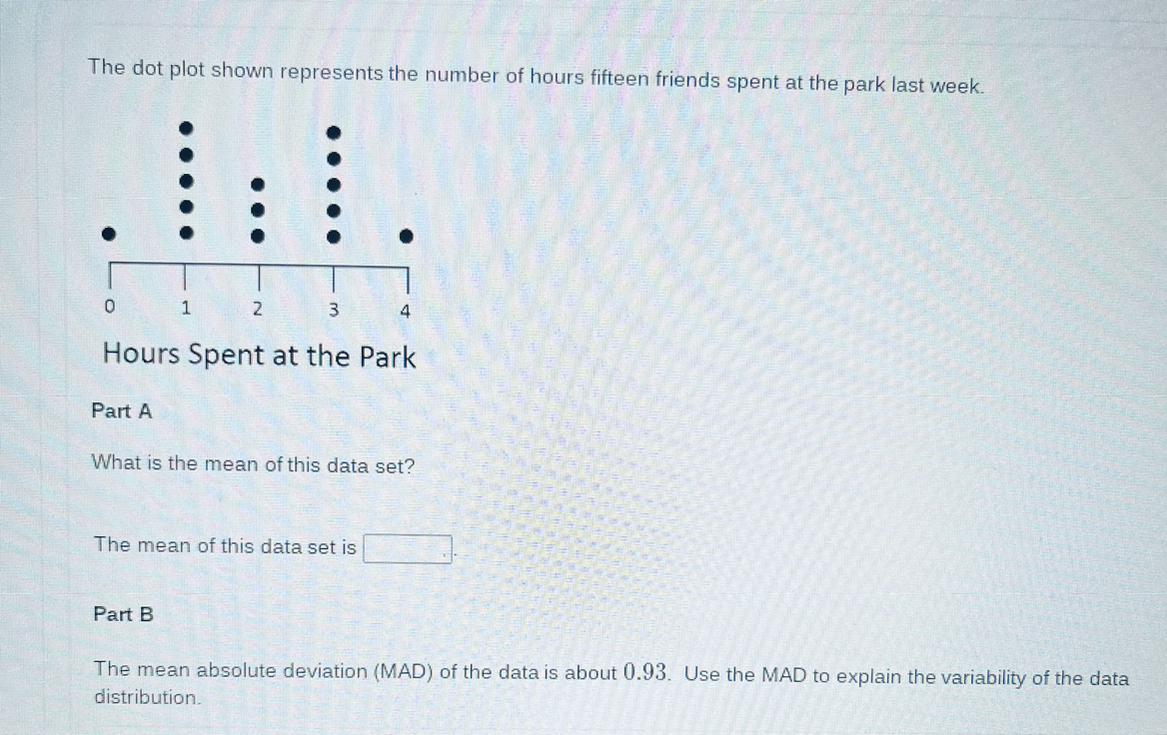
Answers
Explanation for mean:
There are 15 dots total throughout 5 lines. 15/5=3. For the mean you add up the total number of dots and divide it by the amount of categories.
customers arrive randomly at a service point at an average rate of 30 per hours.Assuming a Possition distibution,calculate the probability that
a.no customers arrive in a particular minute.
b.exactly one customer arrives in five minutes.
c.at most one customer arrive in ten minutes.
Answers
Answer:
honestly man I say go with c
35%of students wear glasses.There are 14 students who wear glasses.How many pupils are there in the class?
Answers
Answer: 40 pupils
Step-by-step explanation:
35 14
------- = --------
100 ?
find the denominator.
multiply 14 and 100:
14 x 100 = 1400
divide 1400 by 35
1400/35 = 40
Therefore there are 40 students
x + 2y = 10
y=x-4
Choices are:
(0,4)
(2,6)
(6,2)
(8,0)
Work shown
Answers

Based on this theory, what distance will the handler move from the starting point to the return point if he creates an arc of a circle with radius 70 feet?
Group of answer choices
439.6 feet
3846.5 feet
109.9 feet
1758.4 feet
Answers
The Distance the handler will move from the starting point to the return point will be approximately 439.8204 feet.
The distance the handler will move from the starting point to the return point when creating an arc of a circle with a radius of 70 feet, we need to find the length of the arc.
The formula to calculate the length of an arc is given by:
Length of arc = (θ/360) * 2πr
Where:
θ is the central angle of the arc (in degrees)
r is the radius of the circle
In this case, since the handler is creating a full circle, the central angle is 360 degrees.
Length of arc = (360/360) * 2π * 70
Length of arc = (1) * 2π * 70
Length of arc = 2π * 70
Length of arc = 140π
To find the approximate value in feet, we can use the approximation π ≈ 3.14159.
Length of arc ≈ 140 * 3.14159
Length of arc ≈ 439.8204 feet
Therefore, based on the given theory and using a circle with a radius of 70 feet, the distance the handler will move from the starting point to the return point will be approximately 439.8204 feet.
For more questions on Distance .
https://brainly.com/question/30395212
#SPJ8
How would you solve
"if f(x) / (x - 2) = x ^ 3 + 2x - 4 + 13/(x - 2) what is f(2)"
and
"if f(x) / (x + 3) = 3x ^ 2 - 4x + 2 what is f(-3)"
Answers
The denominator is zero (0/0 is undefined), we cannot determine the exact value of f(-3) using this equation.
To solve the given equations, we need to find the value of the function f(x) for specific values of x.
"If f(x) / (x - 2) = x³ + 2x - 4 + 13/(x - 2), what is f(2)?"
To find f(2), we can substitute x = 2 into the equation and solve for f(2).
Plugging in x = 2, we get:
f(2) / (2 - 2) = 2³ + 2(2) - 4 + 13/(2 - 2)
Since the denominator is zero (2 - 2 = 0), the equation is undefined. Therefore, there is no solution for f(2) in this case.
"If f(x) / (x + 3) = 3x² - 4x + 2, what is f(-3)?"
To find f(-3), we can substitute x = -3 into the equation and solve for f(-3).
Plugging in x = -3, we get:
f(-3) / (-3 + 3) = 3(-3)² - 4(-3) + 2
Simplifying, we have:
f(-3) / 0 = 3(9) + 12 + 2
f(-3) / 0 = 27 + 12 + 2
f(-3) / 0 = 41
Additional information or context is needed to solve for f(-3).
For similar questions on denominator
https://brainly.com/question/20712359
#SPJ8
In a class of 29 students, 20 play an instrument and 18 play a sport. There are 11 students who play an instrument and also play a sport. What is the probability that a student chosen randomly from the class plays a sport and an instrument?
Answers
The probability that a student chosen randomly from the class plays a sport and an instrument is given as follows:
11/29.
How to calculate the probability?A probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
From this problem, we have a total of 29 students, while 11 of these students play both an instrument and a sport, hence the probability that a student chosen randomly from the class plays a sport and an instrument is given as follows:
p = 11/29.
More can be learned about probabilities at https://brainly.com/question/14398287
#SPJ1
A cylinder has a height of 18 cm and a diameter of 12 cm. Calculate the surface area of the cylinder. Give your answer to the nearest integer.
Answers
The surface area of the cylinder is 905 square centimeters
Finding the surface area of the cylinderFrom the question, we have the following parameters that can be used in our computation:
Diameter, d = 12 cm
Height, h = 18 m
This means that
Radius, r = 12/2 = 6 cm
Using the above as a guide, we have the following:
Surface area = 2πr(r + h)
Substitute the known values in the above equation, so, we have the following representation
Surface area = 2π * 6 * (6 + 18)
Evaluate
Surface area = 905
Hence, the surface area is 905 square centimeters
Read more about surface area
brainly.com/question/26403859
#SPJ1
What is the product of 0.1 and 0.3?
Answers
Answer:
Step-by-step explanation:
O.4
Find the area of the shape shown below.
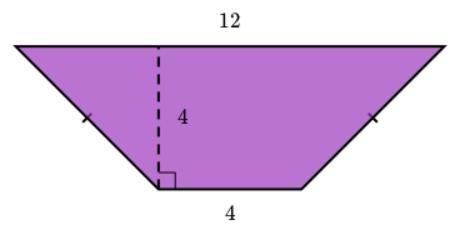
Answers
Answer:
The answer is 32
Step-by-step explanation:
The formula for finding the area of a trapezoid is:
((base 1 + base 2)/ 2 )* h
Now all you have to do is substitute the numbers in.
Note: bases will always be the ones like 12 and 4 in this case. We have just named then 1 and 2.
Answer:
32 square units
Step-by-step explanation:
\(\displaystyle A=\frac{1}{2}(b_1+b_2)h=\frac{1}{2}(12+4)(4)=\frac{1}{2}(16)(4)=\frac{1}{2}(64)=32\)
Note that \(b_1\) and \(b_2\) are the lengths of each base of the trapezoid, so it doesn't matter which is which.
Please help I’m in a hurry
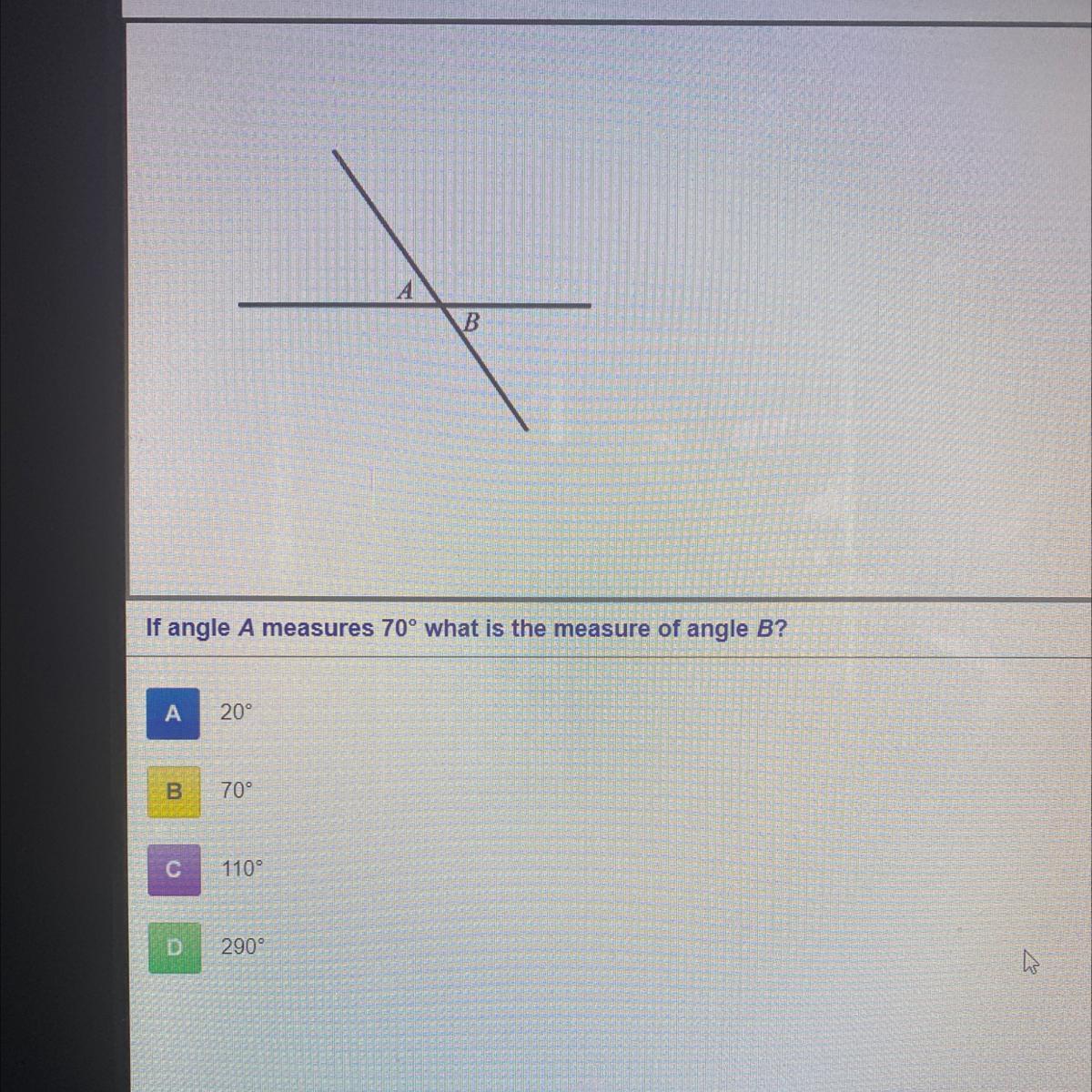
Answers
Answer:
I believe it is A 20,
however id wait for another answer to confirm lol
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
i can compute the derivative of an implicitly-defined function and find the slope of the tangent line to an implicit curve
Answers
Finding the equation of the tangent line by using implicit differentiation is essentially the same as doing it by using ordinary differentiation. Keep in mind that we use normal differentiation to complete the following procedures to determine the equation of the tangent line:
Take the given function's derivative.To get the slope of the tangent line, evaluate the derivative at the specified position.Simplify by entering the provided point and the slope of the tangent line into the \((y-y_{1} ) = m(x-x_{1} )\) formula for the equation of a line.The equation for the tangent line to the given function at the given position is the outcome. The methods we just stated apply when we have a function that isn't explicitly defined for yy and obtaining the derivative needs implicit differentiation; however, in Step 1, we utilize implicit differentiation rather than standard differentiation.
Learn more about Implicit Differentiation here
https://brainly.com/question/11887805
#SPJ4
1 pizza costs £3.20 more than a bottle of coke. The total cost of the items is £19.40 for 3 pizzas and 1 bottle of coke
How much does a pizza cost?
Answers
1 pizza should cost $5.65
Pizza is $5.65 then bottle of coke is $2.45
3 pizzas and coke: ($5.65*3) + $2.45 = $19.4
I solved this by setting up and solving a system of linear equations:
Variables: p = pizza, c = coke
p = c+3.2
3p+c = 19.4
Solve by substitution
3(c+3.2) + c = 19.4
4c+9.6 = 19.4
c = 2.45
Re-plug in:
p = 2.45+3.2
p = 5.65
How many schools have fewer than 50 classrooms

Answers
Answer:
7 schools have fewer than 50 classrooms.
In circle N with � ∠ � � � = 12 4 ∘ m∠MNP=124 ∘ and � � = 13 MN=13, find the area of sector MNP. Round to the nearest hundredth.
Answers
If circle with center N with m∠MNP=124 ∘ and MN=13, the area of sector MNP is approximately equal to 194.86 square units.
To find the area of a sector of a circle, we need to use the formula:
Area of sector = (central angle/360°) x πr²
Where r is the radius of the circle.
In this problem, we know that the central angle m∠MNP is 124° and MN, which is also the radius of the circle, is 13. So we can substitute these values into the formula:
Area of sector = (124/360) x π(13)²
Area of sector ≈ 194.86
Therefore, the area of sector MNP is approximately equal to 194.86 square units.
To learn more about sector click on,
https://brainly.com/question/23857683
#SPJ1
Number patterns 2 3 4 12 13 14 22 23 24 25 26 27 28 29 32 33 34 35 36 37 38 39 42 43 44 45 46 47 48 49 52 53 54 55 56 57 58 59 62 63 64 65 66 67 68 69 72 73 74 75 76 77 78 79 84 82 83 85 86 90 87 88 89 94 92 93 95 96 97 98 99 100 1 11 21 31 41 51 61 71 81 91 5 6 7 8 9 10 15 16 17 18 19 20 30 40 50 60 70 80 2. Start at 2.. Count by 2s. Colour these boxes yellow. 3. Start at 5. Count by 5s. Colour these boxes green. 4. Start at 1. Count by 10s. Colour these boxes red. 5.Count up to 100, by 1s, 2s, 5s, 10s, and 25s. Ask a friend to listen to you. Count forwards and backware Learning Outcome: skip count forward and backward by 2s. 5s. 10s. 25s. and 100s to 1000.

Answers
Answer:
Step-by-step explanation:

Sally can buy 3 pieces of candy for $1.20 or 5 pieces for $2.50, which has a better unit rate? Explain.
Answers
Answer: The 3 pieces of candy- one candy under that costs only 40 cents. The five pieces separated cost 50 cents each
Answer:
3 pieces of candy for $1.20
Step-by-step explanation:
because 1.20/3=0.40
and 2.50/5=0.50
so as you can see it cost less to get 3 pieces then to get 5 pieces
hopefully you understand
if f(x)=x+2/x^2-9 and g(x)=11/x^2+3x
A. find f(x)+g(x)
B. list all of the excluded values
C. classify each type of discontinuty
To receive credit, this must be done by Algebraic methods, not graphing
Answers
The types of discontinuities are: removable discontinuity at x = -3 and vertical asymptotes at x = 0 and x = 3.
A. To find f(x) + g(x), we add the two functions together:
f(x) + g(x) = (x + 2)/(x^2 - 9) + 11/(x^2 + 3x)
To add these fractions, we need a common denominator. The common denominator in this case is (x^2 - 9)(x^2 + 3x). So, we rewrite the fractions with the common denominator:
f(x) + g(x) = [(x + 2)(x^2 + 3x) + 11(x^2 - 9)] / [(x^2 - 9)(x^2 + 3x)]
Simplifying the numerator:
f(x) + g(x) = (x^3 + 3x^2 + 2x^2 + 6x + 11x^2 - 99) / [(x^2 - 9)(x^2 + 3x)]
Combining like terms:
f(x) + g(x) = (x^3 + 16x^2 + 6x - 99) / [(x^2 - 9)(x^2 + 3x)]
B. To find the excluded values, we look for values of x that would make the denominators zero, as division by zero is undefined. In this case, the excluded values occur when:
(x^2 - 9) = 0 --> x = -3, 3
(x^2 + 3x) = 0 --> x = 0, -3
So, the excluded values are x = -3, 0, and 3.
C. To classify each type of discontinuity, we examine the excluded values and the behavior of the function around these points.
At x = -3, we have a removable discontinuity or hole since the denominator approaches zero but the numerator doesn't. The function can be simplified and defined at this point.
At x = 0 and x = 3, we have vertical asymptotes. The function approaches positive or negative infinity as x approaches these points, indicating a vertical asymptote.
Therefore, the types of discontinuities are: removable discontinuity at x = -3 and vertical asymptotes at x = 0 and x = 3.
For more questions on vertical .
https://brainly.com/question/30195815
#SPJ8