Find the solution set of each inequality below, and then determine which inequalities have the same
solution set as -(-8x – 3) < 23. Select all that apply.
A
1
(8x + 3) < -23
B
(10x =
- 20) >-44
1
(8x + 3) >-23
(10
(10x +20) >44
E
(8x + 3) < 23
F-crx
(10x +20) < -44
+
Answers
Answer:
(8x+3)<23 is the same as -(-8x-3)<23
Step-by-step explanation:
-(-8x-3)<23 Original equation
(8x+3)<23 [Remove the parentheses]
It is the same equation as the chosen answer: (8x+3)<23
Answer:
Choice E.
Step-by-step explanation:
-(-8x – 3) < 23
-8x - 3 > -23
-8x > -20
x < 20/8
x < 2.5.
E:-
(8x + 3) < 23
8x < 20
x < 2.5.
Related Questions
10 Find the series solution of the differential equation about to 0 (1 – x)y" + xy' - y = 0, Xo = 0. = =
Answers
We can find the series solution of the differential equation by using the Frobenius method.
When x is near zero, we can find a solution by considering a power series of the form y(x) = a0 + a1x + a2x^2 + ... for which we can express the coefficients of the series recursively. The value x = 0 is called the ordinary point of the differential equation if it can be a point of convergence of the power series. In this case, the given differential equation has an ordinary point at x = 0, hence we can use the power series method to find the solution. Therefore, let's use Frobenius method to solve this differential equation.Explanation:Given differential equation is (1 – x)y" + xy' - y = 0It can be rearranged as, y" + [(x/(1-x))y'] - (1/(1-x))y = 0
This equation can be solved by Frobenius Method using the power series method.
Let y = Σ n=0∞ anxn be a solution to the above differential equation.Substituting y and its first and second derivatives in the given differential equation, we get:Σ n=0∞ [(n + 2)(n + 1)an+2 - an + (n + 1)an+1] xn + Σ n=0∞ [(n + 1)an+1/(1 - x) - an/(1 - x)] xn = 0Equating the coefficients of xn on both sides, we get two equations for an+2 and an+1, which are given by:an+2 = (1/(n + 2)(n + 1) )[(n + 1 - (n + 1)²)an - (n - 1)an-1 ]an+1 = (1/(n + 1)) [an - an+2 /(1 - x)]Therefore, the series solution of the given differential equation is:y(x) = a0 [1 + x + (2x^2)/2! + (5x^3)/3! + (14x^4)/4! + ....] + a1 [0 + 1 + (3x)/2! + (11x^2)/3! + (36x^3)/4! + ...]
Summary:In summary, the power series method (Frobenius method) is used to find the series solution of the given differential equation. The solution is y(x) = a0 [1 + x + (2x^2)/2! + (5x^3)/3! + (14x^4)/4! + ....] + a1 [0 + 1 + (3x)/2! + (11x^2)/3! + (36x^3)/4! + ...].
Learn more about equation click here:
https://brainly.com/question/2972832
#SPJ11
The series solution of the differential equation by using the Frobenius method is y(x) = a₀ [1 + x + (2x²)/2! + (5x³)/3! + (14x⁴)/4! + ....] + a₁ [0 + 1 + (3 x)/2! + (11 x²)/3! + (36 x³)/4! + ...]
Given:
Differential equation is (1 – x)y" + (x)y' - y = 0, It can be rearranged as, y" + [(x/(1-x))y'] - (1/(1-x))y = 0
This equation can be solved by Frobenius Method using the power series method.
Let y = Σ n=0∞ an xn
Σ n=0∞ [(n + 2)(n + 1)an+2 - an + (n + 1)an+1] xn + Σ n=0∞ [(n + 1)an+1/(1 - x) - an/(1 - x)] xn = 0
an+2 and an+1, which are given by:
an+2 = (1/(n + 2)(n + 1) )[(n + 1 - (n + 1)²)an - (n - 1)an-1 ]an+1 = (1/(n + 1)) [an - an+2 /(1 - x)]
Therefore, the series solution of the given differential equation is:
y(x) = a₀ [1 + x + (2 x²)/2! + (5 x³)/3! + (14 x⁴)/4! + ....] + a₁ [0 + 1 + (3x)/2! + (11 x^2)/3! + (36 x³)/4! + ...]
Learn more about Frobenius method here:
brainly.com/question/2972832
#SPJ4
the binomial theorem states that for any real numbers a and b (a b)^n
Answers
The binomial theorem cannot be used to expand expressions of the form (a - b)^n, where n is an even integer and a and b are real numbers.
The binomial theorem states that for any real numbers a and b, and a non-negative integer n, the expression (a+b)^n can be expanded as the sum of the terms in the form:
(a+b)^n = C(n,0) * a^n * b^0 + C(n,1) * a^(n-1) * b^1 + ... + C(n,n) * a^0 * b^n
where C(n,k) denotes the binomial coefficient, which can be calculated using the formula:
C(n,k) = n! / (k! * (n-k)!)
In this expansion, each term represents a product of the powers of a and b, with the exponents summing up to n. The binomial coefficients, C(n,k), indicate the number of ways to choose k items from a set of n items.
So, the binomial theorem allows us to expand expressions involving the sum of two real numbers raised to a power, using the binomial coefficients and the powers of the real numbers.
The binomial theorem is a powerful formula that allows us to expand expressions of the form (a + b)^n, where n is a non-negative integer. Specifically, the theorem states that (a + b)^n = sum from k=0 to n of (n choose k) * a^(n-k) * b^k, where (n choose k) denotes the binomial coefficient, which is equal to n! / (k! * (n-k)!). However, if we let b = -a, then (a + b)^n becomes (a - a)^n = 0^n = 0. Therefore, the binomial theorem cannot be used to expand expressions of the form (a - b)^n, where n is an even integer and a and b are real numbers. In such cases, we need to use alternative methods such as the difference of squares formula or the factor theorem.
Learn more about binomial theorem here: brainly.com/question/30100273
#SPJ11
Question 4 of 10
Which of the following could be the ratio between the lengths of the two legs
of a 30-60-90 triangle?
Check all that apply.
□A. √2:√2
B. 15
□ C. √√√√5
□ D. 12
DE √3:3
OF. √2:√5
←PREVIOUS
SUBMIT

Answers
The ratios that could be the lengths of the two legs in a 30-60-90 triangle are √3:3 (option E) and 12√3 (option D).
In a 30-60-90 triangle, the angles are in the ratio of 1:2:3. The sides of this triangle are in a specific ratio that is consistent for all triangles with these angles. Let's analyze the given options to determine which ones could be the ratio between the lengths of the two legs.
A. √2:√2
The ratio √2:√2 simplifies to 1:1, which is not the correct ratio for a 30-60-90 triangle. Therefore, option A is not applicable.
B. 15
This is a specific value and not a ratio. Therefore, option B is not applicable.
C. √√√√5
The expression √√√√5 is not a well-defined mathematical operation. Therefore, option C is not applicable.
D. 12√3
This is the correct ratio for a 30-60-90 triangle. The ratio of the longer leg to the shorter leg is √3:1, which simplifies to √3:3. Therefore, option D is applicable.
E. √3:3
This is the correct ratio for a 30-60-90 triangle. The ratio of the longer leg to the shorter leg is √3:1, which is equivalent to √3:3. Therefore, option E is applicable.
F. √2:√5
This ratio does not match the ratio of the sides in a 30-60-90 triangle. Therefore, option F is not applicable. So, the correct option is D. 1 √2.
For more such questions on lengths
https://brainly.com/question/28322552
#SPJ8
331 students went on a field trip. Six buses were filled and 7 students traveled in cars. How many students were in each car?
Answers
The number of students in each bus can be found by solving the equation from the given facts and there are 54 students in each bus.
Given that,
Total number of students = 331
Six buses were filled and 7 students traveled in cars.
We have to find the number of students in each bus.
Let x be the number of students in each bus.
Total number of students = (students in 6 buses) + 7
Number of students in 6 buses = 6x
We have the equation,
6x + 7 = 331
6x = 324
x = 54
Hence there are 54 students in each bus.
Learn more about Equations here :
https://brainly.com/question/5025595
#SPJ1
please help me there are 3 more questions please


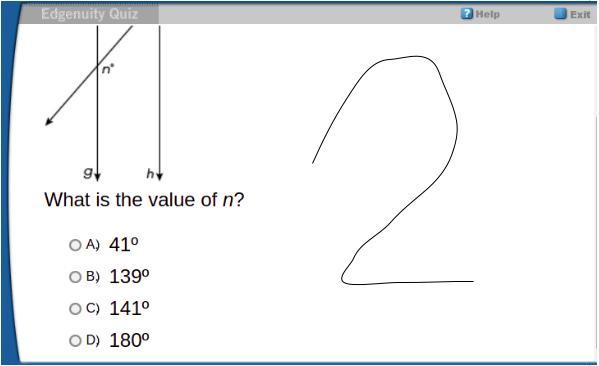
Answers
Answer:
Question 1: C) <5
Question 2: B) 139
Step-by-step explanation:
Question 1: They are looking for an angle with the same degrees as angle 4. There are for angles that have that, 1,4,5,8. When looking for the answer there is only one answer that fits in with those numbers, and that is answer C) <5.
Question 2: They provide us with the first angle of 139 degrees. Angle N corresponds with the first angle. Therefore angle N must be the same as the first angle, equaling 139 degrees.
Explain in words why there is a factor of 2 (or 1/2) in the Virial theorem. Or in other words, what if there is no factor of 2 (i.e. KE=PE) ? Comment, therefore, on a key requirement to apply the Virial Theorem to an astrophysical problem.
Answers
The factor of 2 in the Virial theorem accounts for the balance between average kinetic energy and average potential energy in a system. Without this factor, the theorem would inaccurately represent the energy equilibrium.
The Virial theorem is a fundamental principle in physics that relates the average kinetic energy (KE) of a system to its average potential energy (PE). The theorem states that in a stable system, the average kinetic energy is equal to minus one-half times the average potential energy, or KE = -1/2 PE. The factor of 2 in the theorem is crucial for this relationship to hold.
To understand the significance of this factor, let's consider a hypothetical scenario where there is no factor of 2 in the Virial theorem, meaning KE = PE. In this case, the theorem would suggest an equal balance between kinetic and potential energies. However, this assumption contradicts our understanding of typical astrophysical systems.
Astrophysical systems, such as galaxies, stars, or even gas clouds, often possess a significant amount of gravitational potential energy. If there were no factor of 2, the theorem would imply that the kinetic energy of these systems is equal to the gravitational potential energy. This would imply that the system is on the verge of collapse or expansion, which is not usually the case for stable systems.
The factor of 2 in the Virial theorem accounts for the fact that the average kinetic energy of particles in a system is typically twice as large (in magnitude) as the average potential energy. This factor arises due to the virialization process, where particles oscillate between kinetic and potential energy as they interact with each other. The factor of 2 allows for a more accurate representation of the balance between these energies in a stable system.
In conclusion, the factor of 2 in the Virial theorem is essential to accurately describe the relationship between the average kinetic and potential energies in astrophysical systems. Without this factor, the theorem would fail to capture the typical energy balance observed in stable systems.
The Virial theorem is a powerful tool used in various fields of astrophysics, including the study of galaxies, star clusters, and even the dynamics of gas in the interstellar medium. Understanding its derivation and applications can provide deeper insights into the behavior and evolution of these astronomical systems.
Additionally, exploring the concept of virialization and how it relates to the factor of 2 in the Virial theorem can shed light on the dynamical processes occurring within these astrophysical environments.
Learn more about Virial theorem
brainly.com/question/33291046
#SPJ11
Please help me!!!!! 30 points



Answers
Answer:
The answer to the question in the first picture is the first one, "The thirty students studies for the test; only eight students got As."
I had a difficult time deciding whether the answer to the question in the second picture is the fourth one, "Her philosophy is that respect should not be given; it should be earned." or the first one, "Her philosophy is that respect should not be given, it should be earned." but I'm pretty sure that it is the fourth one. (I'm so sorry if it's wrong!)
The answer to the question in the third picture is the third one, "The new school will have many features: a huge gym, several science labs, and am extensive library."
Step-by-step explanation:
I hope this helps! Have a lovely day!! :)
(also, I'm really sorry if the answer for the second question is wrong)
a motor boat traveling at 18 miles per hour traveled the length of a lake in one-quarter of an hour less time than it took when traveling at 12 miles per hour. what was the length in miles of the lake?
Answers
The length of the lake in miles for the given situation of travelling motor boat is equal to 9 miles.
Let us consider the length of the lake be d in miles.
Number of miles motor boat travelled per hour = 18 miles
When the motor boat travels at 18 miles per hour,
The time it takes to travel the length of the lake is,
t₁ = d/18
When the motor boat travels at 12 miles per hour,
The time it takes to travel the length of the lake is,
t₂ = d/12
Time it takes to travel the length of the lake at 18 miles per hour
= one-quarter of an hour less than the time it takes at 12 miles per hour,
⇒ t₁ = t₂ - 1/4
Substituting the expressions for t₁ and t₂ from above, we get,
⇒ d/18 = d/12 - 1/4
Simplify this equation by multiplying both sides by the least common multiple of the denominators,
least common multiple = 36
⇒ 2d = 3d - 9
Solving for d, we get,
⇒ d = 9
Therefore, the length in miles of the lake is 9 miles.
learn more about miles here
brainly.com/question/29173795
#SPJ4
12 divided by 4/3 =
Answers
Answer:
9
Step-by-step explanation:
Answer:
9
Step-by-step explanation:
Hope this helps!
Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes, and one vertex in the plane.
Answers
The volume of the largest rectangular box in the first octant with three faces in the coordinate planes, and one vertex in the plane is V = xyz, where x, y, and z are the lengths of the sides of the rectangular box.
To find the largest volume, we need to maximize x, y, and z. Since we have three faces in the coordinate planes, one vertex will be at the origin (0, 0, 0). The other two vertices will lie on the coordinate axes.
Let's assume the vertex on the x-axis is (x, 0, 0), and the vertex on the y-axis is (0, y, 0). The third vertex on the z-axis will be (0, 0, z). Since the box is in the first octant, all the coordinates must be positive.
To maximize the volume, we need to find the maximum values for x, y, and z within the constraints. The maximum values occur when the box touches the coordinate planes. Therefore, the maximum values are x = y = z.
Substituting these values into the volume formula, we get V = xyz = x³. Therefore, the volume of the largest rectangular box is V = x³.
Learn more about constraints here
brainly.com/question/32387329
#SPJ11
What is the maximum volume of a rectangular box situated in the first octant, with three of its faces lying on the coordinate planes, and one of its vertices located in the plane?
Multiply (3x2 + y2) by (x2 + 2y2)
Answers
Answer:
3x^4 + 7x^2y^2 + 2y^4
Step-by-step explanation:
(3x^2 + y^2) (x^2 + 2y^2)
3x^4 + 6x^2y^2 + x^2y^2 + 2y^4
3x^4 + 7x^2y^2 + 2y^4
-TheUnknownScientist
An equation for the line whose slope is 4 and which passes thorough the point (-5,3)
Answers
Answer:
y = 4x + 23
Step-by-step explanation:
\(y-y_{1}=m(x-x_{1} )\\y-3=4(x-(-5))\\y-3=4(x+5)\\y-3=4x+20\\y=4x+23\)
The equation of the line is required.
The equation of the line is \(y=4x+23\)
Equation of line\(m\) = Slope of line = 4
Point = \((-5,3)\)
\(x_1=-5\)
\(y_1=3\)
Equation of a line is given by
\(y-y_1=m(x-x_1)\\\Rightarrow y-3=4(x-(-5))\\\Rightarrow y-3=4x+20\\\Rightarrow y=4x+20+3\\\Rightarrow y=4x+23\)
Learn more about equation of line:
https://brainly.com/question/13763238
Potassium-42 has a half-life of 12.4 hours. How much of a 746-gram sample will be left after 62 hours?

Answers
the amount of potassium-42 remaining after 62 hours is approximately 23.31 grams (option B)
Explanation:half life = 12.4 hours
initial amount = 746g
time elapsed = 62 hours
Using the half-life formula:
\(\begin{gathered} N(t)=N_0(\frac{1}{2})^{\frac{t}{t_{_{\frac{1}{2}}}}} \\ N(t)\text{ = amount remaining} \\ N_0\text{ = initial amount = 746g} \\ t\text{ = 62 hours} \\ t_{\frac{1}{2}\text{ }}\text{ = 12.4 hours} \end{gathered}\)Substitute for the values:
\(\begin{gathered} N(t)=N_0(\frac{1}{2})^{\frac{t}{t_{_{\frac{1}{2}}}}} \\ N(t)\text{ = }746(\frac{1}{2})^{\frac{62}{12.5}} \\ N(t)\text{ = }746(\frac{1}{2})^5 \\ N(t)\text{ = }746(\frac{1}{2^5}) \end{gathered}\)\(\begin{gathered} N(t)\text{ = }(\frac{746}{32})^{} \\ N(t)\text{ = }23.3125 \end{gathered}\)Hence, the amount of potassium-42 remaining after 62 hours is approximately 23.31 grams (option B)
NEED ASAP MATH!! 7TH GRADE

Answers
Answer:
b
Step-by-step explanation:
Alain throws a stone off a bridge into a river below.
The stone's height h (in meters above the water). t seconds after Alain threw it, is
modeled by:
h=-4.9+2+10t+18
What is the height of the stone at the time it is thrown?
Answers
Cedarburg's zoo has two elephants. The male elephant weighs 3 3/4 tons and the female
elephant weighs 7/12 of a ton. How much more does the male weigh than the female?
Answers
Answer:
3.16666667 tons
Step-by-step explanation:
hope this helps have a good evening
please answer this question attached

Answers
The equation of the line passing through M and perpendicular to PR would be y = -x + 6.
What is the equation of the line?
An equation of a line is a mathematical expression that describes the relationship between the variables x and y that defines the position of a point on the line. There are several ways to write the equation of a line, including slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), and standard form (ax + by = c).
The midpoint of a line segment is the point that is exactly halfway between the two endpoints of the line. To find the midpoint of a line segment, you need to take the average of the x-coordinates and the y-coordinates of the two endpoints.
Given the line segment Q(-6, 2) and R(10, 6), the midpoint is:
((-6+10)/2 , (2+6)/2) = (2,4)
So the midpoint of the line segment Q(-6, 2) and R(10, 6) is (2,4).
Now find the slope of PR = 6-(-4)/10 = 10/10=1
Hence, the slope of the line passing through M and perpendicular to PR would be = -1.
Now we can form the equation of the line:
y - 4 = -1(x - 2)
y - 4 = -x + 2
y = -x + 6
Hence, the equation of the line passing through M and perpendicular to PR would be y = -x + 6.
To learn more about the equation of a line, visit:
https://brainly.com/question/18831322
#SPJ1
In general, what is the relationship between the standard deviation and variance?
a. Standard deviation equals the squared variance.
b. Variance is the square root of the standard deviation.
c. Standard deviation is the square root of the variance.
d. These two measures are unrelated.
Answers
The relationship between the standard deviation and variance is that the standard deviation is the square root of the variance.
The correct option is -C
Hence, the correct option is (c) Standard deviation is the square root of the variance. Variance is the arithmetic mean of the squared differences from the mean of a set of data. It is a statistical measure that measures the spread of a dataset. The squared difference from the mean value is used to determine the variance of the given data set.
It is represented by the symbol 'σ²'. Standard deviation is the square root of the variance. It is used to calculate how far the data points are from the mean value. It is used to measure the dispersion of a dataset. The symbol 'σ' represents the standard deviation. The formula for standard deviation is:σ = √(Σ(X-M)²/N) Where X is the data point, M is the mean value, and N is the number of data points.
To know more about variance visit:
https://brainly.com/question/14116780
#SPJ11
Find the sum of the first 39 terms of the following series, to the nearest integer
7,15,23,...
Answers
Answer:
6201
Step-by-step explanation:
formula for series in AP
where n is the nth term and a is first term and d is difference between two terms in series \(sum = \frac{n}{2} (2a \: + (n - 1)d)\)
Find the slope to the graph below

Answers
Answer:
-1
Step-by-step explanation:
slope = y/x
-4/4 = -1
A grid model with 100 squares. 73 squares are shaded. What percent of the model is shaded? What is the equivalent ratio? What is the equivalent decimal? What is the equivalent fraction?
Answers
Answer:
73%
Step-by-step explanation:
First, you'll divide the total squares by 100 to get how much is one percent. Then, you divide the shaded squares by the value of 1%. And you'll get how many percents are shaded.
For equivalent decimal, you divide the number by 100.
Then for equivalent decimal, you get the percent and 100.
\(p =100/100=1\\73/1=73\\=0.73\\=\frac{73}{100}\)
Answer:
i have proof
Step-by-step explanation:

fill in the missing number: 0,1,1,2,3,5,8,13,-,34,55
Answers
The missing number of the series is 21.
The given sequence appears to follow the pattern of the Fibonacci sequence, where each number is the sum of the two preceding numbers. The Fibonacci sequence starts with 0 and 1, and each subsequent number is obtained by adding the two previous numbers.
Using this pattern, we can determine the missing number in the sequence.
0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55
Looking at the pattern, we can see that the missing number is obtained by adding 8 and 13, which gives us 21.
Therefore, the completed sequence is:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
To learn more about number here:
https://brainly.com/question/32210789
#SPJ4
The missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55 is 21.
To find the missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55, we can observe that each number is the sum of the two preceding numbers. This pattern is known as the Fibonacci sequence.
The Fibonacci sequence starts with 0 and 1. To generate the next number, we add the two preceding numbers: 0 + 1 = 1. Continuing this pattern, we get:
011235813213455Therefore, the missing number in the sequence is 21.
Learn more:About fill in here:
https://brainly.com/question/182137
#SPJ11
what is the measure of angle x?

Answers
Answer:
Since the value of all angles within a triangle must equal 180 degrees, if you know at least two angles, you can subtract them from 180 to find the missing third angle. If you are working with equilateral triangles, divide 180 by three to find the value of X.
Step-by-step explanation:
Step-by-step explanation:
all Δangle sum = 180°
so, therefore
93° + 52° + x° = 180°
145° + x° = 180°
x° = 180° - 145°
x° = 35°
MARK ME BRAINLISTwrite the sum without sigma notation 3 k=1 (-1)^k 1 sin pi/k
Answers
The sum ∑ k=1^3 (-1)^k * 1 * sin(pi/k) is an example of a finite series. A series is the sum of the terms in a sequence. In this case, the sequence is defined by the terms (-1)^k * 1 * sin(pi/k) for k=1, 2, 3.
The sum of these terms is calculated by adding up each term one by one, which gives us the total value of the series. In this series, the values of k are limited to the integers 1, 2, and 3. For each value of k, we evaluate the product of (-1)^k, 1, and sin(pi/k) and then add up these values to get the sum.
The sine function sin(pi/k) gives the ratio of the side opposite to the angle pi/k in a right triangle with hypotenuse 1. Since pi is a constant, the value of sin(pi/k) changes as k varies, resulting in different terms for the series. The factor (-1)^k alternates between 1 and -1 as k increases, leading to terms that are positive and negative.
The sum of the series can be computed by adding up all the terms. In this case, we obtain the value 3 - (3/2)sqrt(3). This final value is a real number that represents the total value of the sum of the series.
To learn more hypotenuse: brainly.com/question/16893462
#SPJ11
Are the given lines parallel?
y = 1, and y = 5
Answers
Yes, they will be parallel
Your quiz grades are 73, 75, 89, and 91. What is the lowest grade you can obtain and still achieve an average of at least 85?
Answers
ANEXO 2
Identifica los objetos con los que se mide la masa y el volumen, y escribe en donde corresponda.
Manómetro
VOLUMEN
MASA
Pipetas
Fórmula de densidad,
Probetas
Báscula.
Matraz
Balanzas
Fórmula volumen
Vaso de precipitación
Answers
The objects used to measure mass are Balances and Scales. The objects used to measure Volume are Manometer, Pipettes, Graduated cylinders, Flasks, Volumetric flasks and Beakers. Here Density formula can be used to measure both mass and volume.
The problem is asking to match different measuring tools with the measurements they are used for, i.e., mass or volume.
The first tool is a manometer. A manometer is used to measure pressure and not mass or volume, so it does not belong in either category.
The next set of tools are pipettes, graduated cylinders, and volumetric flasks. These tools are all used to measure volume, so they belong in the volume category.
The next set of tools are scales and balances. These tools are used to measure mass, so they belong in the mass category.
The formula for density can be used to calculate the mass of an object given its volume and density, or the volume of an object given its mass and density, so it belongs in both categories.
Finally, a beaker or a graduated cylinder can be used to measure volume, so it belongs in the volume category.
Therefore, the correct categorization of the measuring tools are as follows
Volume
Pipettes
Graduated cylinders
Volumetric flasks
Beaker or graduated cylinder
Mass
Scales
balances
Both
Formula for density
To know more about mass and volume:
https://brainly.com/question/18250402
#SPJ4
In a grou of 6 people 45 like apple 30 like banana 15 like orange .if total number of people who like only two fruit is 22 and they like atleast one of the fruits .find the no. of people who like all the fruit
Answers
To find the number of people who like all three fruits, we can use the principle of inclusion-exclusion.In a group of 6 people, 45 like apples, 30 like bananas, and 15 like oranges.
The total number of people who like only two fruits is 22, and they like at least one of the fruits.
Let's break it down:
- The number of people who like apples only is 45 - 22 = 23.
- The number of people who like bananas only is 30 - 22 = 8.
- The number of people who like oranges only is 15 - 22 = 0 (since there are no people who like only oranges).
To find the number of people who like all three fruits, we need to subtract the number of people who like only one fruit from the total number of people in the group:
6 - (23 + 8 + 0)
= 6 - 31
= -25.
Since we can't have a negative number of people, there must be an error in the given information or the calculations. Please check the data provided and try again.
To know more about inclusion-exclusion visit:
https://brainly.com/question/32375490
#SPJ11
There are no people in the group who like all three fruits. In a group of 6 people, 45 like apples, 30 like bananas, and 15 like oranges. We need to find the number of people who like all three fruits. To solve this, we can use a formula called the inclusion-exclusion principle.
This principle helps us calculate the number of elements that belong to at least one of the given sets.
Let's break it down:
1. Start by adding the number of people who like each individual fruit:
- 45 people like apples
- 30 people like bananas
- 15 people like oranges
2. Next, subtract the number of people who like exactly two fruits. We know that there are 22 people who fall into this category, and they also like at least one of the fruits.
3. Finally, add the number of people who like all three fruits. Let's denote this number as "x".
Using the inclusion-exclusion principle, we can set up the following equation:
45 + 30 + 15 - 22 + x = 6
Simplifying the equation, we get:
68 + x = 6
Subtracting 68 from both sides, we find that:
x = -62
Since the number of people cannot be negative, we can conclude that there are no people who like all three fruits.
In conclusion, there are no people in the group who like all three fruits.
Learn more about inclusion-exclusion principle from the given link:
https://brainly.com/question/32375490
#SPJ11
Plz answer no fake stuff plz

Answers
=======================================================
Explanation:
The first number along the top is 40, and it multiplies with the second number along the side to get 40 x 5 = 200
You can think of it as 4 x 5 = 20, then you tack on an extra 0 to the '4' and to the '2' as well, so it keeps things balanced.
So this explains how choice D is one of the answers.
-------------------------
After 200 fills in that question mark, we'll have these four numbers inside the table: 2400, 420, 200, and 35
Those four values add up to: 2400+420+200+35 = 3055
This shows that choice A is one of the answers.
--------------------------
Finally, choice E is the third answer because along the top we have 40+7 = 47, and along the side we have 60+5 = 65
Put another way, the total top length is the sum of the two smaller pieces of 40 and 7, which explains how the total top length is 47 units long. A similar argument happens for the left side values as well.
We ultimately have a rectangle that is 47 units across in the horizontal direction, and 65 units tall in the vertical direction.
With your calculator, you should note that 47*65 = 3055 to help confirm everything lines up.
--------------------------
Extra info:
Choice B is false because this contradicts choice D.
Choice C is false because it contradicts choice E
Find the value of X , Y, and z in the parallelogram below.

Answers
Answer:
x = 67y = 121z = 65Step-by-step explanation:
We know that:
y - 9 + x + 1 = 180z + 3 + 112 = 180y - 9 + z + 3 = 180x + 1 + 112 = 180y - 9 = 112x + 1 = z + 3y - 9 + x + 1 + z + 3 + 112 = 360Solution of x:
x + 1 + 112 = 180 => x + 113 = 180=> x = 180 - 113=> x = 67Solution of y:
=> y - 9 + x + 1 = 180=> y - 9 + 67 + 1 = 180=> y + 59 = 180=> y = 180 - 59=> y = 121Solution of z:
=> x + 1 = z + 3=> 67 + 1 = z + 3=> 68 = z + 3=> z = 68 - 3=> z = 65Hence, the answers are:
x = 67y = 121z = 65Check:
y - 9 + x + 1 + z + 3 + 112 = 360=> 121 - 9 + 67 + 1 + 65 + 3 + 112 = 360=> 360 = 360Hence, the answers are proved as correct.
Hoped this helped.
\(BrainiacUser1357\)