find the slope of the line that passes through (8,10) and (5,5)
Answers
Answer:
5/3
Step-by-step explanation:
The slope is the rise over run or the change in y over the change in x. One way to find the slope is through the formula, which is \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\). To use this simply plug in the two points. In this case, the expression would be \(\frac{10-5}{8-5}\). This simplifies down to 5/3.
Related Questions
if x=7, which inequality is true?

Answers
Answer:
B
Step-by-step explanation:
Substitute x =7 in each inequality
In A.
\( - 4 + 3 \times 7 < 17 \\ - 4 + 21 < 17 \\ \\ - 17 < 17\)
Which is not true
B.
\( - 7 - 2 \times 7 > 1 \\ - 7 - 14 > 1 \\ - 21 > 1\)
Which is not true.
C.
\(5 - 7 \leqslant 9 \\ - 2 \leqslant 9\)
Which is true
D.
\(1 - 4 \times 7 \geqslant 25 \\ 1 - 28 \geqslant 25 \\ - 27 \geqslant 25 \\ \)
Which is not true
so option C is the right answer
Pleaseee help me I’ve been stuck on this fool like 30 minutes can’t miss this or I restart the whole lesson pleease help

Answers
The properties of equality that shows justification of how the equation is solved is explained below.
How to Apply the Properties of Equality to Solve an Equation?Given the equation, 17/3 - 3/4x = 1/2x + 5, we have the following steps and justification which explains the property of equality that was used:
17/3 - 3/4x = 1/2x + 5 [given]
17/3 - 3/4x - 17/3 = 1/2x + 5 - 17/3 [subtraction property of equality]
3/4x = 1/2x - 2/3 [simplification]
3/4x - 1/2x = 1/2x - 2/3 - 1/2x [subtraction property of equality]
-5/4x = -2/3 [simplification]
-5/4x * -4/5 = -2/3 * -4/5 [multiplication property of equality]
x = 8/15 [simplification]
Learn more about property of equality on:
https://brainly.com/question/1601404
#SPJ1
NO LINKS!! Please help me with this graph

Answers
=========================================================
Explanation:
The three points are at these locations:
A = (10, 6)B = (1,-3)C = (-5, 3)The notation "d(A,C)" means "the distance from A to C". It's equivalent to saying "the length of segment AC".
Then writing \(\left[d(A,C)]^2\) means we'll square that distance.
Use the distance formula to get...
\(A = (x_1,y_1) = (10,6) \text{ and } C = (x_2, y_2) = (-5,3)\\\\d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\d = \sqrt{(10-(-5))^2 + (6-3)^2}\\\\d = \sqrt{(10+5)^2 + (6-3)^2}\\\\d = \sqrt{(15)^2 + (3)^2}\\\\d = \sqrt{225 + 9}\\\\d = \sqrt{234}\\\\\)
This is the exact length of segment AC. That value squares to 234.
\(d = \sqrt{234} \ \to \ d^2 = (\sqrt{234})^2 = 234\\\\\)
The square root and squaring operation cancel each other out. Think of it like fire vs water.
So we really only care about what's under the square root; rather than the entire square root expression itself. Which is nice because we don't have to worry about pesky things like decimal values.
This is why 234 is typed into the first box.
---------------------
Next, use the distance formula to find how far it is from A to B. Square the result to get what you see below.
\(A = (x_1,y_1) = (10,6) \text{ and } B = (x_2, y_2) = (1,-3)\\\\d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\d = \sqrt{(10-1)^2 + (6-(-3))^2}\\\\d = \sqrt{(10-1)^2 + (6+3)^2}\\\\d = \sqrt{(9)^2 + (9)^2}\\\\d = \sqrt{81 + 81}\\\\d = \sqrt{162}\\\\d^2 = (\sqrt{162})^2\\\\d^2 = 162\\\\\)
This is the value of \(\left[d(A,B)\right]^2\)
Now find the distance from B to C, and square the result.
\(B = (x_1,y_1) = (1,-3) \text{ and } C = (x_2, y_2) = (-5,3)\\\\d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\d = \sqrt{(1-(-5))^2 + (-3-3)^2}\\\\d = \sqrt{(1+5)^2 + (-3-3)^2}\\\\d = \sqrt{(6)^2 + (-6)^2}\\\\d = \sqrt{36 + 36}\\\\d = \sqrt{72}\\\\d^2 = \left(\sqrt{72}\right)^2\\\\d^2 = 72\\\\\)
Add this to the previous squared value and we get 162+72 = 234, which matches exactly with the 234 found up toward the top.
We'll write 234 in the 2nd box as well.
This shows that \(\left[d(A,C)\right]^2 = \left[d(A,B)\right]^2+\left[d(B,C)\right]^2\) is a true statement. By the converse of the Pythagorean theorem, we have confirmed this is a right triangle.
In other words, we've shown that \(a^2+b^2 = c^2\) is a true statement (a,b,c are the sides of the right triangle such that c is the hypotenuse).
---------------------
Recall that we found these segment lengths:
\(AB = \sqrt{162} = \text{leg1}\\\\BC = \sqrt{72} = \text{leg2}\\\\AC = \sqrt{234} = \text{hypotenuse}\\\\\)
The legs of a right triangle represent the base and height, in either order. This is because the legs are perpendicular to one another. They form a right (aka 90 degree) angle.
\(\text{area} = \frac{1}{2}*\text{base}*\text{height}\\\\\text{area} = \frac{1}{2}*\text{AB}*\text{BC}\\\\\text{area} = \frac{1}{2}*\sqrt{162}*\sqrt{72}\\\\\text{area} = \frac{1}{2}*\sqrt{162*72}\\\\\text{area} = \frac{1}{2}*\sqrt{11664}\\\\\text{area} = \frac{1}{2}*108\\\\\text{area} = 54\\\\\)
Here are some alternative methods you can follow to find the area of this triangle.
Pick's TheoremShoelace TheoremCreate a bounding box around the triangle. Make the box as small as possible. Find the area of the whole box, and subtract off the smaller pieces outside the triangle.Heron's FormulaAs for verifying the answers, you can use a tool like GeoGebra.
Answer:
\([d(A,C)]^2=\boxed{234}\)
\([d(A,B)]^2+[d(B,C)]^2=\boxed{234}\)
\(\sf Area=\boxed{54}\; units^2\)
Step-by-step explanation:
From inspection of the given diagram:
A = (10, 6)B = (1, -3)C = (-5, 3)If ΔABC is a right triangle, the sum of the squares of the two shorter sides will equal the square of the longest side. This is the definition of Pythagoras Theorem.
Use the distance formula to find the length of each side of the triangle.
\(\boxed{\begin{minipage}{7.4 cm}\underline{Distance between two points}\\\\$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}\)
\(\begin{aligned}d[(A,C)]&=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}\\&=\sqrt{(-5-10)^2+(3-6)^2}\\&=\sqrt{(-15)^2+(-3)^2}\\&=\sqrt{225+9}\\&=\sqrt{234}\end{aligned}\)
\(\begin{aligned}d[(A,B)]&=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\\&=\sqrt{(1-10)^2+(-3-6)^2}\\&=\sqrt{(9)^2+(-9)^2}\\&=\sqrt{81+81}\\&=\sqrt{162}\end{aligned}\)
\(\begin{aligned}d[(B,C)]&=\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}\\&=\sqrt{(-5-1)^2+(3-(-3))^2}\\&=\sqrt{(-6)^2+(6)^2}\\&=\sqrt{36+36}\\&=\sqrt{72}\end{aligned}\)
Therefore:
The longest side of the triangle is line segment AC.The two shorter sides of the triangle are line segments AB and BC.\(\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}\)
Therefore, the triangle is a right triangle if:
\([d(A,B)]^2+[d(B,C)]^2=[d(A,C)]^2\)
Substitute the found side lengths into the formula:
\(\implies [\sqrt{162}]^2+[\sqrt{72}]^2=[\sqrt{234}]^2\)
\(\implies162+72=234\)
\(\implies 234=234\)
Hence proving that ΔABC is a right triangle.
To find the area of a right triangle, half the product of the two shorter sides:
\(\begin{aligned}\implies \sf Area &= \dfrac{1}{2}bh\\&=\dfrac{1}{2} \cdot [d(A,B)] \cdot [d(B,C)]\\&=\dfrac{1}{2} \cdot \sqrt{162} \cdot \sqrt{72}\\&=\dfrac{1}{2} \cdot \sqrt{162 \cdot 72}\\&=\dfrac{1}{2} \cdot \sqrt{11664}\\&=\dfrac{1}{2} \cdot \sqrt{108^2}\\&=\dfrac{1}{2} \cdot 108\\&=54 \sf \; units^2\end{aligned}\)

a) angle of line of From a point O in the school compound, Adeolu is 100 m away on a bearing N 35° E and Ibrahim is 80 m away on a bearing S 55° E. (a) How far apart are both boys? (b) (c) What is the bearing of Adeolu from point O, in three-figure bearings? What is the bearing of Ibrahim from point O, in three figure bearings? A boy walks 5 km due North and then 4 km due East. (a) Find the bearing of his current posi- tion from the starting point. (b) How far is the boy now from the start- ing point? A boy runs 200 m on a bearing of 230°.
Answers
a) Angle of line of sightFrom a point O in the school compound, Adeolu is 100 m away on a bearing N 35° E and Ibrahim is 80 m away on a bearing S 55° E. (a) How far apart are both boys? (b) (c) What is the bearing of Adeolu from point O, in three-figure bearings? What is the bearing of Ibrahim from point O, in three-figure bearings?The angle of the line of sight of Adeolu from the point O is given by:α = 90 - 35α = 55°.The angle of the line of sight of Ibrahim from the point O is given by:β = 90 - 55β = 35°.a) By using the Sine Rule, we can determine the distance between Adeolu and Ibrahim as follows:$
\frac{100}{sin55^{\circ}} = \frac{80}{sin35^{\circ}
100 sin 35° = 80 sin 55°=57.73 mT
herefore, both boys are 57.73 m apart. b) The bearing of Adeolu from the point O can be determined as follows:OAN is a right-angled triangle with α = 55° and OA = 100. Therefore, the sine function is used to determine the side opposite the angle in order to determine AN.
Thus:$$sin55^{\circ} = \frac{AN}{100}$$AN = 80.71 m.
To find the bearing, OAD is used as a reference angle. Since α = 55°, the bearing is 055°.
Therefore, the bearing of Adeolu from the point O is N55°E. c) Similarly, the bearing of Ibrahim from the point O can be determined as follows:OBS is a right-angled triangle with β = 35° and OB = 80. Therefore, the sine function is used to determine the side opposite the angle in order to determine BS.
Thus:$$sin35^{\circ} = \frac{BS}{80}$$BS = 46.40 m.
To find the bearing, OCD is used as a reference angle. Since β = 35°, the bearing is 035°.Therefore, the bearing of Ibrahim from the point O is S35°E. A boy walks 5 km due North and then 4 km due East. (a) Find the bearing of his current posi- tion from the starting point.
(b) How far is the boy now from the start- ing point?The boy's position is 5 km North and 4 km East from his starting position. The Pythagorean Theorem is used to determine the distance between the two points, which are joined to form a right-angled triangle. Thus
:$$c^2 = a^2 + b^2$$
where c is the hypotenuse, and a and b are the other two sides of the triangle. Therefore, the distance between the starting position and the boy's current position is:$$
c^2 = 5^2 + 4^2$$$$c^2 = 25 + 16$$$$c^2 = 41$$$$c = \sqrt{41} = 6.4 km$$
Therefore, the boy is 6.4 km from his starting point. (a) The bearing of the boy's current position from the starting point is given by the tangent function.
Thus:$$\tan{\theta} = \frac{opposite}{adjacent}$$$$\tan{\theta} = \frac{5}{4}$$$$\theta = \tan^{-1}{\left(\frac{5}{4}\right)}$$$$\theta = 51.34^{\circ}$$
Therefore, the bearing of the boy's current position from the starting point is N51°E.
For such more question on triangle
https://brainly.com/question/1058720
#SPJ8
can anyone please help me with this I am struggling

Answers
Answer:
B, D
Step-by-step explanation:
for it to be symmetrical, you have to rotate it so it matches the other triangle.
What is -2.1(3p-5)?
Answers
Answer:
-6.3p+10.5
Step-by-step explanation:
Answer:
-6.3p +10.5
Step-by-step explanation:
Multiply -2.1 by 3p and that equals -6.3p then multiply -2.1 by -5 which equals 10.5 and that is your eqaution -- -6.3p + 10.5
In a random sample of 60 computers the mean repair cost was $150 with a standard deviation of $36. Construct a 99 % interval for the
population mean.
Answers
The required confidence interval of the random sample of the given data is (151.5456, 148.4544).
What is confidence interval?Statisticians use confidence intervals to gauge vulnerability in an example variable. For instance, a scientist chooses various examples haphazardly from a similar populace and figures a certainty stretch so that each example might be able to perceive how it might address the genuine worth of the populace variable. The subsequent datasets are different where a few stretches incorporate the genuine populace boundary and others don't.
According to question:In an random sample of 60 PCs, the mean fix cost was $150, with the populace standard deviation being $36.
Standard deviationσ = $36, μ = $150 , n = 60
Value of z for 99% confidence interval is 2.576
Then,
Confidence interval = μ±z(σ/n)
Confidence interval = $150 ± 2.576(36/60)
Confidence interval = $150 ± 1.5456
Confidence interval = $150 +1.5456 , $150 - 1.5456
Confidence interval = 151.5456, 148.4544
Thus, required interval is (151.5456, 148.4544).
To know more about confidence interval visit:
brainly.com/question/24131141
#SPJ1
One year, the population of a city was 143,000. Several years later it was
138,710. Find the percent decrease.
Answers
Answer:
One year, the population of a city was 143,000. Several years later it was
138,710. Find the percent decrease - 3% decrease.
Use the image to answer the question.
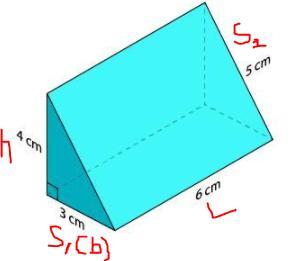
Triangular prism with height 6. The sides of the base are 3, 4, & 5, with a right angle between the sides with lengths 3 & 4. All measurements are in centimeters.
© 2018 StrongMind
What is the surface area of the figure in square centimeters?
Enter your answer as a number, like this: 42

Answers
120 cm² is the surface area of the right triangular prism
How to find the surface area of a right triangular prism?The surface area of a right triangular prism can be determined using the formula below:
A = (S₁ + S₂ + h)L + bh (Check the attached image for the labeling)
Given: S₁ = 3 cm, S₂ = 5 cm, h = 4 cm, L = 6cm and b = 3 cm
Substitute these values into the formula:
A = (S₁ + S₂ + h)L + bh
A = (3 + 5 + 4)6 + 3(4)
A = (18)6 + 12
A = 120 cm²
Therefore, the surface area of the right triangular prism is 120 cm²
Learn more right triangular prism on:
https://brainly.com/question/26979119
#SPJ1
Plz help I need help
Answers
Answer:
The ratios are proportional ratios
Answer:
Step-by-step explanation:
The ratios are proportional
\(\dfrac{5}{12}=\dfrac{5*2}{12*2}=\dfrac{10}{24}\)
Write the fraction as a mixed number 10/20
Answers
Which expression is equivalent to one over five m − 20?
Answers
Answer:
1/5m - 20 = 1/5(m - 100)
Step-by-step explanation:
What statement is true about - 14 and -8?
Answers
Answer:
they are both negative numbers and -14 < -8 (less than)
Step-by-step explanation:
Help help help math math

Answers
(3) 5(x-2)/3 = -x +2 (3)
5(x-2) = -x + 2 (3)
5(x-2)= -3x+6
5x - 10 = -3x+6
Then add 10 on both sides
5x-10=-3x+6
+10 +10
5x=-3x+16
Then add 3x on both sides, then divide by 8 to find x
5x=-3x+16
+3x +3x
8x=16
8x/8= 16/8
x = 2
Answer:
x = 2
Step-by-step explanation:
Help please I’m so lost

Answers
The required distance between the foot of the ladder to the wall is 14.14 feet.
Using trigonometry, we can find that the distance from the wall (x) is given by:
x = 20sin(45°)
= 20(√2/2)
= 10√2 feet.
This is approximately equal to 14.14 feet when rounded to two decimal places.
The correct answer is C. 14.14 feet.
Learn more about trig ratios here:
https://brainly.com/question/14977354
#SPJ1
Please help please please

Answers
sketch the graph of the function3.) \(y = \sqrt{x} \)I got (0,0) as my answer but I want to see if I got it correct!!
Answers
You have to graph the following function
\(y=x\)This is a linear function with slope m=1, this means that each time x increases one unit, y also increases one unit.
To sketch this function you have to choose at least two values of x and determine the corresponding value of y.
Then plot the points and draw the line.
I will make a table with 5 points of the line:
Now what's left is to plot all points and link them with a line:
![sketch the graph of the function3.) [tex]y = \sqrt{x} [/tex]I got (0,0) as my answer but I want to see](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/1uOVM12IECjZ7pFlisGoLLykaFw7B3R8.png)
![sketch the graph of the function3.) [tex]y = \sqrt{x} [/tex]I got (0,0) as my answer but I want to see](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Iqayc0v6CHG53P8t8NYliLQDn2hPH4nL.jpeg)
PLEASE HELP
Which of the following values for X will make relation A shown below, a function?
A=(5,3),(4,9),(7,2),(x,6)
3
4 (I know 4 is wrong)
5
7
Answers
The value of x that makes the relation a function is 3.
Option A is the correct answer.
We have,
A = (5, 3), (4, 9), (7, 2), (x, 6)
Given the points (5, 3), (4, 9), (7, 2), and (x, 6), we need to ensure that x does not repeat in the relation.
If we substitute the given values of x (3, 4, 5, 7) into the relation, we find:
For x = 3: (3, 6)
For x = 4: (4, 6)
For x = 5: (5, 6)
For x = 7: (7, 6)
Now,
A function can not have the same output for the same input.
So,
(4, 6) and (4, 9) are not possible.
(5, 6) and (5, 3) are not possible.
(7, 6) and (7, 2) are not possible.
And,
(3, 6) is possible
Thus,
The value of x that makes a function is 3.
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
Can someone help Pleasaseee

Answers
Answer:
i think it's 1.8.
Step-by-step explanation:
why? bc if u add 6/20 + 1.5 = 1.8
i think it's 1.8, im not sure, hopefully it's correct!!
Answer:
1.8
Step-by-step explanation:
you just simplify -6/20 into a decimal and you get .3 then you add it to 1.5.
Solve F=9/5C+32 for C.
A.F−32/9
B.5/F−32
C.9/5(F−32)
D.5/9(F−32)
Answers
Answer:
C
Step-by-step explanation:
Use the image below to find y

Answers
Answer:
y = 7
Step-by-step explanation:
since the 2 triangles are congruent then corresponding angles are congruent , so
∠ R = ∠ F , that is
13y - 1 = 90 ( add 1 to both sides )
13y = 91 ( divide both sides by 13 )
y = 7
16 families went on a trip which cost them Rs 2,16,352. How much did each
family pay?
Answers
Given that 16 families went on a trip and the cost of the trip was Rs. 2,16,352.The amount paid by each family is to be determined by unitary method Hence each family paid Rs.13522
Now, let's solve this by using the method of unitary method. To find the cost of 1 family trip, we will divide the total cost of the trip by the number of families.2,16,352 / 16 = 13,522 So, the cost of the trip per family is Rs. 13,522.Hence, each family paid Rs. 13,522 for the trip.
to know more about unitary method
https://brainly.com/question/28276953
Answer:
Step-by-step explanation
1. The total cost of the trip for all 16 families is Rs 2,16,352.
2. To find out how much each family paid, we need to divide the total cost by the number of families: Rs 2,16,352 ÷ 16.
3. When we do the division, we get the result: Rs 13,522.
Now let's check if this result is correct:
1. If each family paid Rs 13,522 for the trip, then the total cost for all 16 families would be: 16 × Rs 13,522 = Rs 2,16,352.
2. This is exactly the same as the total cost given in the problem statement.
So we have shown that each family paid **Rs 13,522** for the trip
QUESTION 1
Find the remaining sides of a 30° -60°-90° triangle if the shortest side is 3.
Answers
Answer:
the other sides are 6 and 3√3
Step-by-step explanation:
Answer:
x = 6
Step-by-step explanation:
Right Triangle
We are given a right triangle whose shortest side has a length of 3 units. This side must be opposite to the smallest acute angle of 30°.
The triangle is shown in the figure attached.
The tangent ratio relates the opposite side with the adjacent side. The formula can be applied to the angle of 30° as follows:
\(\displaystyle \tan 30^\circ=\frac{\text{opposite leg}}{\text{adjacent leg}}\)
\(\displaystyle \tan 30^\circ=\frac{3}{y}\)
Solving for y:
\(\displaystyle y=\frac{3}{\tan 30^\circ}\)
Since:
\(\tan 30^\circ=\frac{1}{\sqrt{3}}\)
\(\displaystyle y=3\sqrt{3}\)
Now applying the sine to find the hypotenuse x:
\(\displaystyle \sin 30^\circ=\frac{\text{opposite leg}}{\text{hypotenuse}}\)
\(\displaystyle \sin 30^\circ=\frac{3}{x}\)
Solving for x:
\(\displaystyle x=\frac{3}{\sin 30^\circ}\)
Since:
\(\sin 30^\circ=\frac{1}{2}\)
\(\displaystyle x=\frac{3}{\frac{1}{2}}\)
x = 6

The length l of a rectangle is decreasing at a rate of 3 cm/sec while the width w is increasing at a rate of 3 cm/sec. When l=5 cm and w=12 cm, find the rates of change of the area, the perimeter, and the lengths of the diagonals of the rectangle. Determine which of these quantities are increasing, decreasing, or constant.
a) The rate of changes of the area of the rectangle is _______ cm^2/sec
Is the area increasing, decreasing, or constant?
b) The rate of change of the perimeter of the rectangle is ____ cm/sec.
Is the perimeter increasing, decreasing, or constant?
c) The rate of change of the length of the diagonals of the rectangle is ____ cm/sec.
Is the length of the diagonals increasing, decreasing, or constant.
Answers
Answer:
1) dA/dt = -21 cm²/s and Area is decreasing
2)dP/dt = 0 and perimeter is constant
3) dD/dt = 21/13 cm/s and diagonal is increasing
Step-by-step explanation:
We are given that;
length l of a rectangle is decreasing at a rate of 3 cm/sec.
Thus, dl/dt = -3 cm/sec
Also, the width w is increasing at a rate of 3 cm/sec. Thus;
dw/dt = 3 cm/sec
When l=5 cm and w=12 cm;
A) Area is given by the formula;
A = lw
The rate at which area is increasing is;
dA/dt = l(dw/dt) + w(dl/dt)
Plugging in the relevant values;
dA/dt = 5(3) + 12(-3)
dA/dt = 15 - 36
dA/dt = -21 cm²/s
This is less than 0.thus, A is decreasing.
B) Formula for perimeter is;
P = 2l + 2w
rate of change of perimeter is;
dP/dt = 2(dw/dt) + 2(dl/dt)
Plugging in the relevant values, we have;
dP/dt = 2(-3) + 2(3)
dP/dt = 0
Thus,Perimeter is constant
C) the length of the diagonal of a rectangle is given by;
D = √(w² + l²)
Rate of change of diagonal is;
dD/dt = [2w(dw/dt) + 2l(dl/dt)]/(2√(w² + l²))
2 will cancel out in numerator and denominator to give;
dD/dt = [w(dw/dt) + l(dl/dt)]/(√(w² + l²))
Plugging in the relevant values gives;
dD/dt = [12(3) + 5(-3)]/(√(12² + 5²))
dD/dt = (36 - 15)/13
dD/dt = 21/13 cm/s
This is greater than 0.
Thus, diagonal is increasing.
URGENT!! ILL GIVE
BRAINLIEST!!!! AND 100 POINTS!!!!!

Answers
Answer: A 143 degrees because angle 5 is a congruent to angle one
Step-by-step explanation:
\((3x^{3} y^{2} z)(2xy^{5} z^{5}\)
Answers
- BRAINLIEST answerer ❤️
pleaseeeeeeee help
What is the probability of rolling a sum of 14?
Answers
Answer: 7.0%
Step-by-step explanation:
The probability of rolling a sum of 14 is 7.0% because 15/216 = 7.0%
The probability of rolling a sum of 14 is \(\frac{1}{72}\) or 0.014.
What is probability?Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event. For an experiment having 'n' number of outcomes, the number of favorable outcomes can be denoted by x. The formula to calculate the probability of an event is as follows.
Formula of probability
Probability(Event) = \(\frac{Favorable Outcomes}{Total Outcomes}\)
According to the question
rolling a sum of 14
As the maximum sum of two dice is 6+6 = 12
Therefore ,
we will take 3 dices
Now ,
As each dice have 6 different digits and can be repeated
i.e
Total outcomes = 6 * 6 * 6 = 216
Favorable outcome :
(6,6,2) or (2,6,6) or (6,2,6) = 3 ways
Now,
By using the formula of probability
Probability(Event) = \(\frac{Favorable Outcomes}{Total Outcomes}\)
Substituting the value in the formula
Probability(Event) = \(\frac{3}{216}\)
Probability(Event) = \(\frac{1}{72}\) or 0.014
Hence, the probability of rolling a sum of 14 is \(\frac{1}{72}\) or 0.014
To know more about probability here:
https://brainly.com/question/11234923
#SPJ3
CAN ANYONE HELP ME I WILL MARK AS BRAINLIEST
Solve the word problem and Write the statements.
Grade 3 students used three rolls of ribbons measuring 300 metres, 286 metres and 258 metres for dance in primary Concert. Find the total length of ribbons.
Answers
= 844 meters
A math class has a total of 31 students. The number of females is seven less than the number of meals. How many miles and how many females are in the class?
Answers
Answer:
Male-19&Female-13
Step-by-step explanation:
See the image for solution
Hope it helps
Have a great day

Find the lenghts of the sides of the rectangle ABCD shown on the coordinate plane. Suppose you double the length of each side. What would be the new coordinates of point C if the coordinate of point A stay the same

Answers
Looking at the diagram,
each small box represents one unit
The number of units from A to B is 4 units
The number of units from B to C is 3 units
Thus, the length of rectangle ABCD is 4 units and its width is 3 units.
The original coordinates are
A(0, 0)
B(0, 4)
C(3, 4)
D(3, 0)
If