Find the slope of the line -5,6 and -3,-3

Answer: in the third draw 33.33% people eliminated.

Step-by-step explanation:

Answer:

the percent error in the student's measurement is 4.65%.

Step-by-step explanation:

The percent error can be calculated using the formula:

| (measured value - actual value) / actual value | * 100%

In this case, the measured value is 2.7 grams and the actual value is 2.58 grams. Substituting these values into the formula, we get:

| (2.7 - 2.58) / 2.58 | * 100% = 4.65%

Rounding this to the nearest hundredth of a percent, we get a percent error of 4.65%.

Therefore, the percent error in the student's measurement is 4.65%.

Answer:

x = 31°

Step-by-step explanation:

the sum of the 3 angles in a triangle = 180° , that is

x + 54° + 95° = 180°

x + 149° = 180° ( subtract 149° from both sides )

x = 31°

Answer:

The slope is -1/2

Step-by-step explanation:

The joint relative Frequency of students who do not like to run and enjoy swimming, based on the given two-way frequency table, is approximately 62.16%.

The joint relative frequency of students who do not like to run and enjoy swimming, we need to find the intersection of the row and column corresponding to those categories in the two-way frequency table.

Given the following information from the table:

Likes running: 28

Does not like running: 46

Column totals: 74

Enjoys swimming: 62

Enjoys cycling: 90

Row totals: 110

The joint relative frequency, we divide the number of students who do not like running and enjoy swimming by the total number of students:

Joint relative frequency = (Number of students who do not like running and enjoy swimming) / (Total number of students)

From the table, the number of students who do not like running and enjoy swimming is given as 46.

Total number of students is given as 74.

Joint relative frequency = 46 / 74

Calculating this value, we find that the joint relative frequency is approximately 0.6216, which is equivalent to 62.16%.

Therefore, the joint relative frequency of students who do not like to run and enjoy swimming is approximately 62.16%.

In conclusion, the joint relative frequency of students who do not like to run and enjoy swimming, based on the given two-way frequency table, is approximately 62.16%.

To know more about Frequency .

https://brainly.com/question/28821602

#SPJ8

The answer is either 0.2 as a decimal or 1/5 as a fraction.

Probability is a measure of the likelihood of an event occurring, expressed as a number between 0 and 1, with 0 indicating impossibility and 1 indicating certainty.

To estimate the probability that Maria succeeds at fewer than 7 free-throws in a sample of 10, we need to sum up the number of successful free-throws in each simulated sample that are less than 7, and then divide by the total number of simulated samples.

From the dot plot, we can see that there are 5 simulated samples with fewer than 7 successful free-throws.

Therefore, the estimated probability that Maria succeeds at fewer than 7 free-throws in a sample of 10 is:

P(fewer than 7 successes) ≈ 5/25 ≈ 0.2

To know more fraction visit:

https://brainly.com/question/11782774

#SPJ1

The answer of the given question based on the scatterplot for determining  when she will reach 10,000 songs the answer is Maria will reach 10,000 songs in approximately 13.33 months, or about 14 months.

Slope is  measure of  steepness or incline of  line. In geometry and mathematics, slope is defined as  ratio of the change in  y-coordinates to  change in  x-coordinates between two distinct points on  line. This is often represented by  letter "m".

To determine when Maria will reach 10,000 songs, we need to find the point on the line of best fit where the y-value is 10,000.

From the scatterplot, we can estimate that the line of best fit intersects the y-axis at approximately 2000. This means that the initial number of songs downloaded was 2000.

Next, we need to find the slope of the line of best fit. Let's choose the points (5, 6500) and (10, 9500).

The slope of the line passing through these two points is:

slope = (y2 - y1)/(x2 - x1) = (9500 - 6500)/(10 - 5) = 600 songs per month

This means that Maria is downloading 600 songs per month on average.

Finally, we can use the slope-intercept form of a line to find the x-value when the y-value is 10,000:

y = mx + b

10,000 = 600x + 2000

8000 = 600x

x = 13.33

Therefore, Maria will reach 10,000 songs in approximately 13.33 months, or about 14 months.

To know more about Slope-intercept form visit:

https://brainly.com/question/18314949

#SPJ1

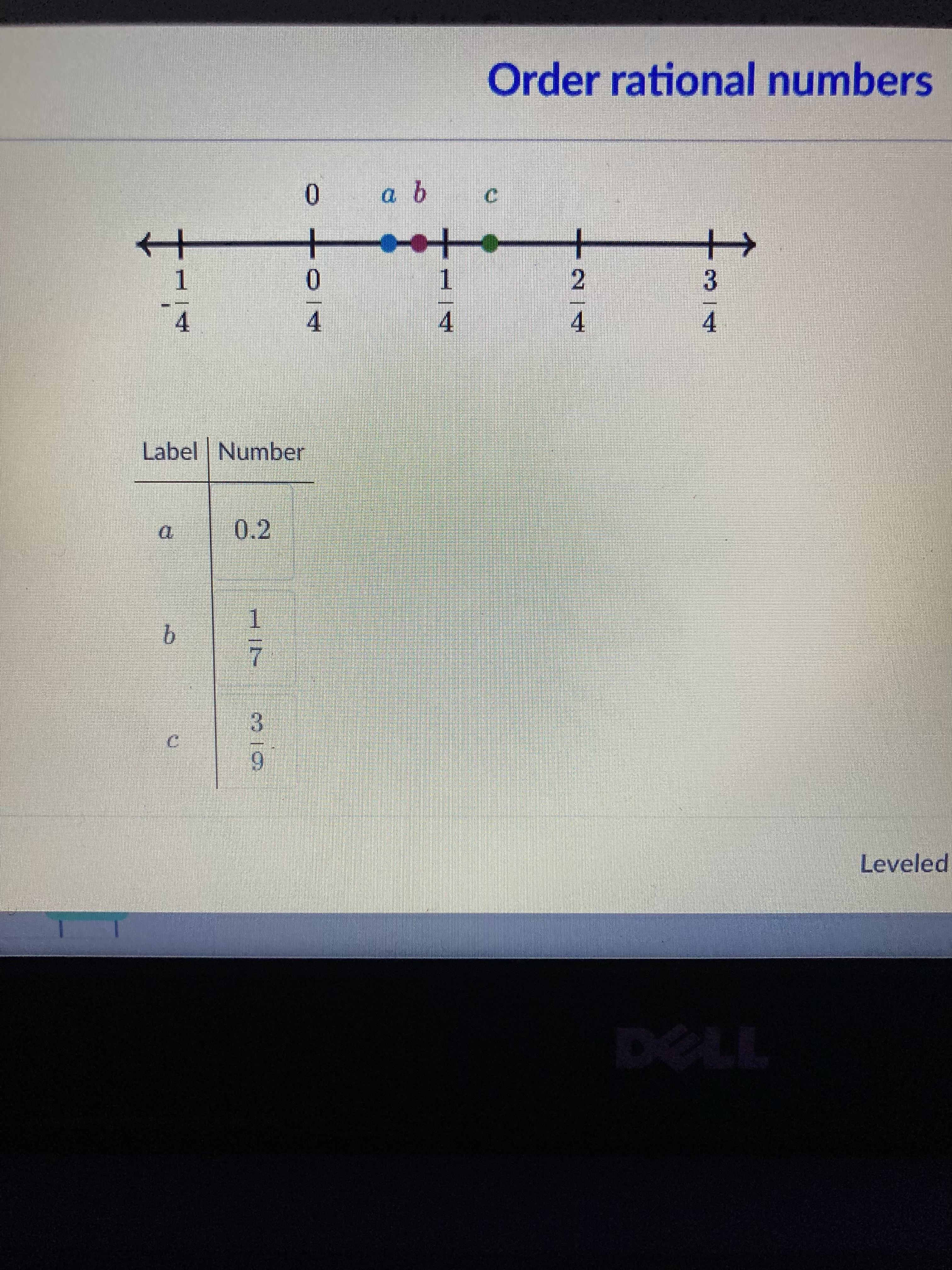
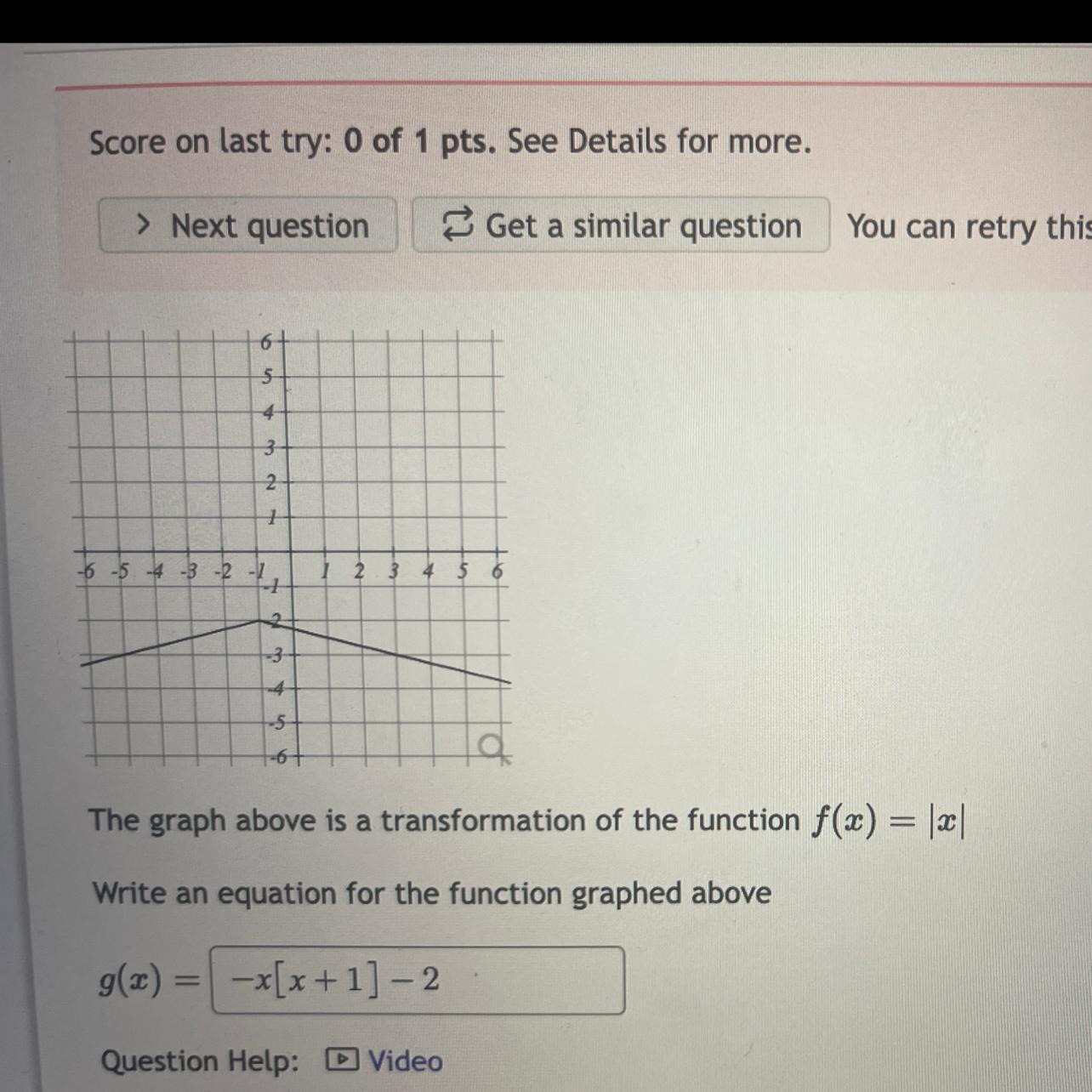
Answer:

Step-by-step explanation:

The length of this line segment is the distance between its endpoints A and B. So, a line segment is a piece or part of a line having two endpoints. Unlike a line, a line segment has a definite length.

Answer: DA = 6

====================================================

Explanation:

The triangles are similar, allowing us to make the proportion below

DB/DA = DA/DC

Plug in the given values. Cross multiply and solve for x

DB/DA = DA/DC

9/DA = DA/4

9*4 = (DA)*(DA)

36 = (DA)^2

(DA)^2 = 36

DA = sqrt(36)

DA = 6

The length of DA is exactly the geometric mean of the lengths BD and DC

geometric mean of x and y = sqrt(x*y)

Answer:

13 1/2

Step-by-step explanation:

think of 9 as 9/1

whenever you divide fractions you must multiply by the reciprocal of the second fraction

9/1 ÷ 2/3 becomes 9/1 × 3/2

= 27/2 or 13 1/2

Answer:

Step-by-step explanation:

im assuming were solving for k so we wanna get it by itself

9k - 18 = -6

start by adding 18 to both sides

9k = 12

then divide both sides by 9

k = 12/9

hope this helps <3

Answer:

the answer is

k= 4/3

Step-by-step explanation:

9k-18=-6

9k=-6+18

9k=12

k= 12/9

simplify it which gives k=4/3 or in decimal form 1.333

Answer:81%

Step-by-step explanation:

Answer:

60% tiger trout

Step-by-step explanation:

First, do 22+18=  40

Then, when doing % its always out of 100. So, 100 - 40= 60%

Which means, there were 60% Tiger trout.                                                                                                                                                            

Answer:

12.5 %

Step-by-step explanation:

There are 8 total sections, and only one of them is yellow. So if we spun it eight times, the possibility of getting yellow is one time. As a result, 1/8 is 12.5%

The speed of the ball after one second is given as follows:

9.175 m/s.

The speed function is the derivative of the position function, which is graphed in this problem.

The position function, in meters, for a projectile's height, is given as follows:

h(t) = -4.9t² + v(0)t + h(0).

In which:

From the graph, the initial height is given as follows:

h(0) = 6.

When t = 4, h = 2.5, hence the initial velocity is obtained as follows:

2.5 = -4.9(4)² + 4v(0) + 6

4v(0) = 2.5 - 5 + 4.9(4)²

4v(0) = 75.9

v(0) = 75.9/4

v(0) = 18.975.

Then the position function is of:

h(t) = -4.9t² + 18.975t + 6.

The velocity function is the derivative of the position, hence:

v(t) = -9.8t + 18.975.

Then the velocity after one second is of:

v(1) = -9.8 + 18.975 = 9.175 m/s.

More can be learned about position and velocity at https://brainly.com/question/24786395

#SPJ1

The projectile reaches its maximum height after 15 seconds.

What is a derivative of a function?

In calculus, the derivative of a function is a measure of the rate at which the function is changing at a given point. It is defined as the slope of the tangent line to the graph of the function at that point.

To find the time at which the projectile reaches its maximum height, we need to find the value of t that maximizes the function h = -13t²+390t.

The first step is to find the derivative of the function h with respect to t. The derivative of a function tells us the rate at which the function is changing at a given point, and it is a useful tool for analyzing the behavior of the function.

The derivative of h with respect to t is:

h' = (-26t) + 390

Next, we set the derivative equal to 0 and solve for t:

0 = (-26t) + 390

26t = 390

t = 15

This tells us that the maximum value of the function h occurs at t = 15 seconds.

Hence, the projectile reaches its maximum height after 15 seconds.

To learn more about the derivative of a function, visit:

#SPJ1

The projectile reaches its maximum height after 15 seconds.

What is a derivative of a function?

In calculus, the derivative of a function is a measure of the rate at which the function is changing at a given point. It is defined as the slope of the tangent line to the graph of the function at that point.

To find the time at which the projectile reaches its maximum height, we need to find the value of t that maximizes the function h = -13t²+390t.

The first step is to find the derivative of the function h with respect to t. The derivative of a function tells us the rate at which the function is changing at a given point, and it is a useful tool for analyzing the behavior of the function.

The derivative of h with respect to t is:

h' = (-26t) + 390

Next, we set the derivative equal to 0 and solve for t:

0 = (-26t) + 390

26t = 390

t = 15

This tells us that the maximum value of the function h occurs at t = 15 seconds.

Hence, the projectile reaches its maximum height after 15 seconds.

To learn more about the derivative of a function, visit:

https://brainly.com/question/21399458

#SPJ1

(a) After 25 years 47.37g of the initial sample left in the sample. (b) 12.83 years takes  the initial sample to decay half of its original amount.

Given:

\(A(t) = 200 e^{-0.054t}\)

Substituting 25 for t in the expression, we get:

A(25) = 200e⁰.⁰⁵⁴ × 25

         = 47.37 g

Thus, after 25 years, there will be 47.37g of the initial sample left in the sample.

(b.) 12.83 years takes the initial sample to decay half of its original amount.

We want to find t such that

\(A(t) = 200e^{0.054} \times t\)

where, t = 100.

Solving for t, we get:

\(200e^{0.054} \times t = 100\)

Dividing both sides by 200 and applying the natural logarithm to both sides, we get:

0.054 × t = ln(0.5)

Therefore,

\(t = \frac{\ln(0.5)}{0.054}\)

  = 12.83 years.

To know more about isotope questions visit here: https://brainly.com/question/18766773

#SPJ1

The expansion will be 64d^6 + 1152d^5 + 9720d^4 + 43740d^3 + 98415d^2 + 145458d + 729

We can expand (2d+3)^6 using the binomial theorem, which states that:

(a + b)^n = nC0 * a^n * b^0 + nC1 * a^(n-1) * b^1 + nC2 * a^(n-2) * b^2 + ... + nCn-1 * a^1 * b^(n-1) + nCn * a^0 * b^n

where nCk is the binomial coefficient, given by:

nCk = n! / (k! * (n-k)!)

Expanding (2d+3)^6 using this formula, we get:

(2d+3)^6 = 6C0 * (2d)^6 * 3^0 + 6C1 * (2d)^5 * 3^1 + 6C2 * (2d)^4 * 3^2 + 6C3 * (2d)^3 * 3^3 + 6C4 * (2d)^2 * 3^4 + 6C5 * (2d)^1 * 3^5 + 6C6 * (2d)^0 * 3^6

Simplifying each term using the binomial coefficient formula, we get:

(2d+3)^6 = 1 * 64d^6 * 1 + 6 * 32d^5 * 3 + 15 * 16d^4 * 9 + 20 * 8d^3 * 27 + 15 * 4d^2 * 81 + 6 * 2d * 243 + 1 * 1 * 729

Simplifying each term further, we get:

(2d+3)^6 = 64d^6 + 1152d^5 + 9720d^4 + 43740d^3 + 98415d^2 + 145458d + 729

Learn more about theorem on;

https://brainly.com/question/343682

#SPJ1

The equation of the line in fully simplified slope-intercept form is y = x + 7.

We have,

From the graph,

The coordinates of the line are:

(0, 7), (-7, 0), and (-2, 5).

We can use any coordinates the line touches on the graph.

We will use,

(0, 7) and (-7, 0)

The equation can be written in the form y = mx + c

m = (0 - 7) / (-7 - 0)

m = -7/-7

m = 1 ______(1)

And,

(0, 7) = (x, y)

So,

y = mx + c ______(2)

7 = 1 x 0 + c

7 = c

c = 7 ______(3)

Now,

From (1), (2), and (3).

y = x + 7

Thus,

The equation of the line in fully simplified slope-intercept form is y = x + 7.

Learn more about equation of a line here:

https://brainly.com/question/23087740

#SPJ1

Answer:

I wish I've known, but try using Symbo-Lab or Math-Way. They help a lot. Step-by-step explanation:

The money loaned at 9% annual interest was 1500 and the money loaned at 11% annual interest was 19000.

Let the amount of money loaned at 9% be x

the amount of money loaned at 11% be y

According to the question,

Total money loaned = 20,500

Thus the equation formed is,

x + y = 20,500 ------ (i)

Simple interest is calculated by

I = P * r * t

where I is the simple interest

r is the rate of interest

t is the time

Thus, the interest on x = 0.09x

the interest on y = 0.11y

Total interest gained = 2,225

Thus the equation formed is,

0.09x + 0.11y = 2225 -------(ii)

Multiply (i) by 0.09

0.09x + 0.09y = 1845

Subtract the above from (ii)

0.02y = 380

y = 19000

x = 1500

Learn more about Equation:

https://brainly.com/question/28871326

#SPJ1

Answer:

Step-by-step explanation:

67

Alijah's taxable income puts him in the first tax bracket, over $8,350 but not surpassing $33,950. Hence, his tax due is a base of $835 plus 15% of the income that exceeds $8,350. This results in a total tax payable of $850. Option B is the correct answer.

Alijah's taxable income falls within the first bracket of the tax table given, being over $8,350 but not over $33,950.

This bracket requires him to pay a tax of $835.00 plus 15% of the amount over $8,350.

He has a surplus of $100 over the $8,350 threshold (i.e., $8,450 - $8,350), and 15% of $100 equals $15.

Therefore, the total tax he owes would be the fixed amount of $835.00 plus the $15.00 calculated, which sums up to $850.00.

Thus, looking at the provided options, option B ($850.00) would be the correct answer.

Learn more about Income Tax here:

https://brainly.com/question/34135935

#SPJ2

The series of the transformation will be reflected across the x-axis, translating 9 units to the Right and 2 units down. Then the correct options are A and C.

A point, line, or mathematical figure can be converted in one of four ways, and each has an effect on the object's structure and/or position. Picture, after translation, refers to the object's ultimate organization and placement.

The translation does not change the shape and size of the geometry. But changes the location.

The reflection does not change the shape and size of the geometry. But flipped the image.

The series of the transformation will be reflected across the x-axis, translating 9 units to the Right and 2 units down. Then the correct options are A and C.

More about the transformation of the shape link is given below.

https://brainly.com/question/27224339

#SPJ1

The complete question is attached below.

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.

Based on the figure on the graph, match the described transformations with the transformed figures.

Reflected across the x-axis

Rotated 180° clockwise

Translated 9 units to the Right and 2 units down

Reflected across the y-axis

Inequality x < 8 represents the real-world problem where Bradley makes less than $8 per hour.

a relationship between two expressions or values that are not equal to each other is called 'inequality.

Let x be the hourly wage that Bradley makes.

We can represent the given information as:

x < 8

x less than eight.

The inequality x < 8 represents the real-world problem where Bradley makes less than $8 per hour.

Hence,  inequality x < 8 represents the real-world problem where Bradley makes less than $8 per hour.

To learn more on Inequality click:

https://brainly.com/question/28823603

#SPJ1

Answer: the amount of money Bradley makes per hour, <, 8, d < 8

Step-by-step explanation:

I got it right on the math assignment.

Answer: If 7+5i is a zero of a polynomial function of degree 5 with coefficients, then so is its conjugate 7-i5.

Step-by-step explanation:

Given: 7+5i is a zero of a polynomial function of degree 5 with coefficients

Here, 7+5i is a complex number.

So, it conjugate (\(\overline{7+5i}=7-5i\)) is also a zero of a polynomial function.

Hence, if 7+5i is a zero of a polynomial function of degree 5 with coefficients, then so is its conjugate 7-i5.

If 7+5i is a zero of a polynomial function of degree 5 with coefficients, then so is its conjugate which is 7 - 5i

The standard form of writing complex numbers with real and imaginary values is expressed as:

z = x + iy

The conjugate of the complex number will be y = x - iy

Given the polynomial 7 + 5i. If 7+5i is a zero of a polynomial function of degree 5 with coefficients, then so is its conjugate which is 7 - 5i

Learn more here: https://brainly.com/question/18018849

An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.

By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;

f(x) = |x|

y = A|x + B| + C

g(x) = -1/4|x + 1| - 2

In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.

Read more on absolute value function here: brainly.com/question/28308900

#SPJ1

The equation for the plane that contains the line and is perpendicular to the plane 2 · x + y - 3 · z = - 4 is - 10 · x + 17 · y - z = 76.

From the equation of the plane 2 · x + y - 3 · z = - 4 we know that its normal vector is (2, 1, - 3). Hence, we have found two direction vectors and already know a point, which are part of this parametric equation:

(x, y, z) = (- 3, 4, 5) + t · (3, 2, 4) + u · (2, 1, - 3)     (1)

The normal vector of the plane is equal to the cross product of the direction vectors of (1):

\(\vec n = (3, 2, 4) \,\times\,(2, 1, -3)\)

\(\vec n = \left|\begin{array}{ccc}\hat{i}&\hat{j}&\hat{k}\\3&2&4\\2&1&-3\end{array}\right|\)

\(\vec n = (-6-4,8+9, 3-4)\)

\(\vec n = (-10, 17, -1)\)

Since the plane contains the point (x, y, z) = (- 3, 4, 5), then we find that the independent constant of the equation of the plane is:

- 10 · x + 17 · y - z = k

- 10 · (- 3) + 17 · 4 - 5 = k

30 + 51 - 5 = k

k = 76

The equation for the plane that contains the line and is perpendicular to the plane 2 · x + y - 3 · z = - 4 is - 10 · x + 17 · y - z = 76.

To learn more on planes: https://brainly.com/question/1962726

#SPJ1

Answer:

It is the top right graph.

The pencils at first were 18. Students borrow some and this number is not given, but we can call this number x (that is, unknown).

6 pencils are left at the end of the day, and this means;

That means 12 pencils were borrowed.

Also answer option 2 is the correct equation to arrive at the correct answer

Answer:

Step-by-step explanation:

Converting all fractions to decimal (for easier comparison) :

Hence,

The amount of the element, Francium, that will remain after 2 hours is 31.25 grams.

To determine how much francium will be left after 2 hours, we need to calculate the number of half-lives that occur within that time period.

Given that the half-life of francium is 22 minutes, we can calculate the number of half-lives in 2 hours (120 minutes):

Number of half-lives = (Total time elapsed) / (Half-life)

Number of half-lives = 120 minutes / 22 minutes ≈ 5.4545

Since we can't have a fraction of a half-life, we take the integer part, which is 5.

Each half-life represents a halving of the amount of francium. So, after 5 half-lives, the remaining amount of francium can be calculated using the formula:

Remaining amount = Initial amount * (1/2)^(Number of half-lives)

Given that the initial amount is 1000 grams, we can calculate the remaining amount after 2 hours:

Remaining amount = 1000 grams * \((1/2)^5\)

Remaining amount ≈ 1000 grams * 0.03125

Remaining amount ≈ 31.25 grams

Therefore, after 2 hours, approximately 31.25 grams of francium will be left.

More on half-life can be found here: https://brainly.com/question/31666695

#SPJ1