Find the slope and the y-intercept of the line.
y = 8x - 1
Answers
Answer:
y = - 1
you basically replace with a 0 and multiply 8 and 0 which leaves you with y = -1
Related Questions
what is the quotient for 5/6 deided by 5/24
Answers
Answer: 4/1
Step-by-step explanation: Find the reciprocal of the divisor
Reciprocal of 5/24: 24/5
Now, multiply it with the dividend
So,
5/6 ÷ 5/24= 5/6 × 24/5= 5 × 24/ 6 x 5 = 120/30
After reducing the fraction, the answer is
4/1
Look over Chuck's work What is incorrect about the way Chuck interpreted his problem? What should have been a clue to Chuck that something was wrong?

Answers
The probability that a random student will be taking both Algebra 2 and Chemistry is 0.0136 or 1.36%.
To find the probability that a random student will be taking both Algebra 2 and Chemistry, we need to use the concept of conditional probability.
Let's denote the event of taking Algebra 2 as A and the event of taking Chemistry as C. We are given that P(A) = 0.08 (8% probability of taking Algebra 2) and P(C|A) = 0.17 (17% probability of taking Chemistry given that the student is taking Algebra 2).
The probability of taking both Algebra 2 and Chemistry can be calculated using the formula for conditional probability:
P(A and C) = P(C|A) * P(A)
Substituting the given values:
P(A and C) = 0.17 * 0.08
P(A and C) = 0.0136
Therefore, the probability that a random student will be taking both Algebra 2 and Chemistry is 0.0136 or 1.36%.
It is important to note that the probability of taking both Algebra 2 and Chemistry is determined by the intersection of the two events, which means students who are taking both courses. In this case, the probability is relatively low, as it depends on the individual probabilities of each course and the conditional probability given that a student is taking Algebra 2.
For more such questions on probability visit:
https://brainly.com/question/25839839
#SPJ8
in the diagram, AB is parallel to DE. Also, DE is drawn such that the length of DE is half the length of AB. If sin A=0.5, then what is sin E?

Answers
Answer:
I got sin E = 0.5
Thus answer choice C being the correct choice
Hope this helps ;)
Step-by-step explanation:
For given diagram, sin(E) = 0.5
What is transversal?"It is a line that passes through two lines in the same plane at two distinct points."
What are parallel lines?"These are the lines in the plane that are at equal distance from each other and never meet."
For given question,
AB is parallel to DE.
We can observe that, the line segment AE is transversal.
So, ∠DEF and ∠FAB are alternate interior angles.
We know, when a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
⇒ ∠FAB = ∠DEF
⇒ ∠A = ∠E
⇒ sin(A) = sin(E)
As, sin(A) = 0.5
⇒ sin(E) = 0.5
Therefore, sin(E) = 0.5
Learn more about the alternate interior angles here:
https://brainly.com/question/22853173
#SPJ2
Lesson 1.10: Daniel works at least 30 hours a week. He works as a math tutor
and as a teacher. The number of hours Daniel works as a tutor (y) is at most
twice the number he works as a teacher (x).
• Write the set of inequalities that represents the constraints of the situation
and state a point (x, y) that is the feasible region.
Answers
The set of inequalities that represents the constraints of the situation is y ≤ 2x, x + y ≥ 30 and a point (x, y) that is the feasible region is (10, 20)
How to write the set of inequalities that represents the constraints of the situation and state a point (x, y) that is the feasible region.The given parameters are:
Number of hours = at least 30 hours a week
This means that
x + y ≥ 30
Also, we have:
The number of hours Daniel works as a tutor (y) is at most twice the number he works as a teacher (x).
This means that
y ≤ 2x
Substitute y ≤ 2x in x + y ≥ 30
x + 2x ≥ 30
This gives
3x ≥ 30
Divide
x ≥ 10
Substitute x ≥ 10 in y ≤ 2x
y ≤ 2 x 10
Evaluate
y ≤ 20
Hence, the set of inequalities that represents the constraints of the situation is y ≤ 2x, x + y ≥ 30 and a point (x, y) that is the feasible region is (10, 20)
Read more about inequalities at
https://brainly.com/question/24372553
#SPJ1
In the figure below S is the center of the circle. Suppose that JK = 2x-2, LK= 12, SN= 5 and SP= 5. Find x and PL.

Answers
Since the radius SR is perpendicular to the chord LK, it divides the chord in two segments with equal length, so we can find PL:
\(\begin{gathered} LK=2\cdot PL \\ 2\cdot PL=12 \\ PL=6 \end{gathered}\)Since SN and SP have the same length, the chords LK and JK also have the same length, so:
\(\begin{gathered} JK=LK \\ 2x-2=12 \\ 2x=14 \\ x=7 \end{gathered}\)So the value of x is 7.
The spinner of the compass is two congruent isosceles triangles connected by their bases as shown in the diagram. The base of each of these triangles is 2 centimeters and the legs are 5 centimeters. 2 congruent isosceles triangles are connected by their bases. A circle is drawn around the triangles. If the metal used to construct the spinner costs $13. 25 per square centimeter, how much will it cost to make this part of the compass? Round to the nearest cent. Cost = $.
Answers
The total cost of the two to make this part of the compass will be equal to $129.85.
Given to us
The base of the isosceles Triangle = 2 cm
The length of the legs of the triangle = 5 cm
The metal used to construct the spinner costs $13. 25 per square centimeter,
What is the area of a single isosceles triangle?We know that the area of a triangle can be written as,
\(\rm Area =\sqrt{s(s-a)(s-b)(s-c)}\)
where the value of s is \(\dfrac{a+b+c}{2}\).
Substitute the value,
\(s=\dfrac{5+5+2}{2} = 6\)
Area of the triangle
\(\rm Area =\sqrt{6(6-5)(6-5)(6-2)} = 4.8989 \approx 4.9\ cm^2\)
What is the area of two isosceles triangles?We already know the area of an isosceles triangle, therefore the area of the two isosceles triangles will be 9.8 cm².
how much will it cost to make this part of the compass?The cost to make this part of the compass will be equal to,
9.8 x $13.25 = $129.85
Hence, the total cost of the two to make this part of the compass will be equal to $129.85.
Learn more about Isosceles triangles:
https://brainly.com/question/7915845

range of f(x)=3x^2-30x-9
Answers
Answer:
y ≥ -84
Step-by-step explanation:
-84 id the vertex so it is the lowest possible value for the range
(c) In a test of a new package design, you drop a carton of a dozen eggs from a height of 1 foot and count the number of broken eggs
Answers
The number of broken eggs will give you an idea of how well the new package design protects the eggs from impacts. If there are no broken eggs, the package design may be effective. However, if there are several broken eggs, the package design may need to be improved to provide better protection.
When testing a new package design, it is important to simulate real-world conditions as much as possible. In this case, dropping a carton of a dozen eggs from a height of 1 foot is a good way to simulate the types of impacts that the package may experience during shipping and handling.
To conduct the test, you will need to follow these steps:
Obtain a carton of a dozen eggs and the new package design.Place the eggs inside the package according to the manufacturer's instructions.Find a suitable location to drop the package from a height of 1 foot. Make sure the area is clear and there is nothing that could interfere with the drop or damage the package.Drop the package from a height of 1 foot.Open the package and examine the eggs. Count the number of broken eggs.
The number of broken eggs will give you an idea of how well the new package design protects the eggs from impacts. If there are no broken eggs, the package design may be effective.
However, if there are several broken eggs, the package design may need to be improved to provide better protection.
To know more about package design, refer here:
https://brainly.com/question/28527314#
#SPJ11
Part B: Melissa designed the kite shown and would like to know the minimum amount of fabric needed to cover the kite. Each unit is 1 inch,
48 in
69 in
286 in
572 in?
Answers
Answer:
69.4 inches
Step-by-step explanation:
A kite is a quadrilateral (has four sides and four angles) with two pairs of congruent adjacent sides. The diagonals of a kite are perpendicular to each other.
To prove that quadrilateral ADBC is a kite, the diagonals of the kite have to be perpendicular to each other.
AD ⊥ BC.
Since adjacent sides are equal to each other, hence:
BC = BD, AC = AD
The coordinate of the vertices are A(11, 0), B(11, 26), C(0, 18) and D(22, 18)
\(BC=\sqrt{(0-11)^2+(18-26)^2} =13.6\ unit\\\\AC=\sqrt{(0-11)^2+(18-0)^2} =21.1\ unit\)
BC = BD, AC = AD
Perimeter of kite = BC + BD + AC + AD = 2BC + 2AC = 2(13.6) + 2(21.1) = 69.4 units = 69.4 inches

Answer: 69
Step-by-step explanation:
an open box is made out of cardboard by cutting out equal-sized squares from each corner. you are given a piece of cardboard that is 24 in by 24 in. what size should the squares be, so that you maximize the volume of the box?
Answers
As the cardboard is square and the sides are 24 inches each, then the maximize volume of the box is 1024 cm³.
Let each side of the square cut off from each corner be x cm
Then the base of the box will be of side (24 − 2x) cm and the height of the box will be x cm
Then volume of box V=(24−2x)(24−2x)x
V=(24 − 2x) ²x
V=4x³ - 96x² + 576x -------------------------------------(i)
Differentiating with respect to x, we get
dV/dx =12x ² − 192x +576
⇒ dV/dx = 12( x² -16x + 48) ---------------------------- (ii)
For maximum volume dV/dx =0
⇒12(x² − 16x + 48)=0
⇒ x² -16x +48 =0
⇒ x² - 12x - 4x + 48 =0
⇒ x(x - 12) - 4 (x - 12)
⇒ (x - 12) (x - 4) =0
⇒ x = 12 or 4
Again differentiating, we get,
d²V/ dx² = 2x - 16 -------------------------------- (iii)
At x = 12,
d²V/dx² = 2× 12 - 16
= 24 - 16
= 8
∴ V is minimum at x = 12 at x = 8
At x = 4
d²V/dx² = 2× 4 - 16
= -8
∴ V is maximum at x=4 at x = -8
∴ Maximum volume
V = (24− 2×4)( 24 − 2×4)×4
= (24 - 8)(24-8) ×4
= 16 × 16 × 4
= 1024 cm³
Therefore, the maximize volume of the box is 1024 cm³.
Learn more about Volume:
https://brainly.com/question/28815550
#SPJ4
Marshall knows that he burns 235 calories by walking for 30 minutes. This week, Marshall walked for 360 minutes. How many calories did Marshall burn by walking this week?
625
1,410
2,820
7,050
Answers
Calories burned for 1 min = 235/30 Cals
So, Calories burned for 360 mins = (360 x Calories per 1 min)
= 360 x 235/30
= 12 x 235
= 2,820 Calories
Hence, the correct answer is 2,820
What is the central of the circle?.
Answers
The central angle is the ratio of arc length and radius.
What is a Central Angle?
The central angle is the angle that a circle's arc occupies in its centre. The arms of the central angle are formed by the radius vectors. In other words, it's an angle whose vertex is the centre of a circle and whose arms, which have the circle's two radii as their arms, cross at two separate positions. These two points make an arc when they are combined. The angle that this arc at the circle's centre subtends is known as the central angle.
According to the central angle, we state that:
An arc's angle at the circle's centre is twice as large as its angle at any other point along the circle's circumference.
OR
The angle subtended by the arc in the opposite segment of the circle is twice as large as the angle at the centre of the circle.
Hence,
The central angle is the ratio of arc length and radius.
To learn more about the central angle, visit:
brainly.com/question/23636799
#SPJ4
5. Prolific uses the bike in his trunk to find a nearby gas station with a mechanic to fix his rental
car. He rides 1.5 mi to the first gas station, where they say the next gas station may have a
mechanic. He then rides 1.6 mi to the next gas station, which also has no mechanic. The
following gas stations at 1.8 mi, 2.1 mi, and 2.5 mi away all have no mechanics available, but
confirm that there is a mechanic at the following gas station.
A. Assuming the rate remains constant, what equation will determine the distance of
the N gas station?
B.
If the pattern continues, how many miles will Prolific bike to get to the mechanic at
the 6th gas station?
Answers
Prolific will bike 2 miles to get to the mechanic at the 6th gas station if the pattern continues.
Assuming the rate remains constant, we can use the equation d = rt, where d is the distance, r is the rate, and t is the time. In this case, we want to find the equation to determine the distance of the Nth gas station.
Let's analyze the given information:
The first gas station is 1.5 miles away.
From the second gas station onwards, each gas station is located at a distance 0.1 miles greater than the previous one.
Based on this pattern, we can write the equation for the distance of the Nth gas station as follows:
d = 1.5 + 0.1(N - 1)
B. To find the distance Prolific will bike to get to the 6th gas station, we can substitute N = 6 into the equation from part A:
d = 1.5 + 0.1(6 - 1)
= 1.5 + 0.1(5)
= 1.5 + 0.5
= 2 miles
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Additive Inverses are numbers that add to make-101/11
Answers
The aditive inverse of a number is given by itself multiplied by -1. Then if we have any number x its additive inverse is -x and their sum is:
\(x-x=0\text{ for all values of x}\)Then theanswer is the second option, 0.
Write an equation and slope intercept form for the line with the slope 2 and the Y intercept 5(Please use 2 points for the graph) (THIS IS ONE QUESTION, I do an online program where this is considered ONE question)equation =
Answers
The slope - intercept form of a line is given by the equation:
In this case, we know that m=2 and y=5. So, the equation of this line will be:
To graph it, we need to plot two points and then join them both. These points could be:
Graphing:



(a) find the volume of the region e that lies between the paraboloid z−242x22y2 and the cone z−2sx21y2
Answers
Volume of "region" which lies between the paraboloid z = 24 - x² - y² and the cone z = 2√x² + y² is 536.2 cubic units.
In order to find the volume, we first convert in the polar-coordinate;
We get,
Cone : z = 2√x² + y² ⇒ 2r; and
Paraboloid : z = 24 - x² - y² ⇒ 24 - r²;
So, the point of intersection can be found by;
2r = 24 - r²,
r² - 24r + 2r = 0,
r = 4, -6.
Since, r≥0, we have r=4;
The intervals are : 0≤r≤4 and 0≤θ≤2π;
So, the Volume is written as : \(\int\limits^{2\pi}_0 \int\limits^4_0\) ((24-r²) - 2r)r.dr.dθ
⇒ \(\int\limits^{2\pi}_0 \int\limits^4_0\) (24 - 2r - r²)r.dr.dθ
⇒ \(\int\limits^{2\pi}_0 \int\limits^4_0\) (24r - 2r² - r³)dr.dθ
⇒ \(\int\limits^{2\pi}_0\) [12r² - 2r³/3 - r⁴/4]⁴₀,
⇒ 2π [192 - 128/3 - 64] = 512π/3 ≈ 536.2 cubic units.
Therefore, the volume of the region is 536.2 cubic units.
Learn more about Volume here
https://brainly.com/question/30785714
#SPJ4
The given question is incomplete, the complete question is
Find the volume of the region that lies between the paraboloid z = 24 - x² - y² and the cone z = 2√x² + y².
What is the value of f(x) when x = -3?
Graph and answer choices below.

Answers
The value of the function at x = -3 is -1
Function -An association between a number of inputs and outputs is called a function. A function is, to put it simply, an association of inputs where each input is connected to exactly one output.
For each function, there is a corresponding range, codomain, and domain.
The relation is referred to as a function if each element in set A has exactly one and only one image in set B. The function must have a single relationship with each possible input value and be true for all possible input values. A connection from a non-empty set B that has A as its domain and never has the same first member in two different ordered pairs is called a function.
Given that a graph of y= f(x), we need to find f(-3)
The graph tells the value of y when x = -3 is -1
Hence, The value of the function at x = -3 is -1
To learn more about the function visit,
brainly.com/question/21145944
#SPJ1
. The graph of 2x – y = 3 is shown on the coordinate grid.
Which ordered pair is NOT in the solution set of 2x – y > 3? (2, 0) (2, 1) (1, –3) (3, –1)

Answers
Answer
2,1
Step-by-step explanation:
all the others or on one side besides that one with is on the line
The ordered pair which is not in the solution set of 2x – y > 3 is that which is a solution of the graph of 2x – y = 3 and is; (2, 1)
According to the question;
We are required to determine which ordered pair is NOT in the solution set of 2x – y > 3Evidently, among the choices of coordinates; only (2, 1) is a solution of the equation 2x – y = 3.
By testing;
2(2) - 1 = 33 = 3.As such, since (2,1) is a solution of the equation 2x – y = 3, it can't also be a solution of 2x – y > 3.
Read more:
https://brainly.com/question/21766426
out of 330 racers who started the marathon, 293 completed the race, 29 gave up, and 8 were disqualified. what percentage did not complete the marathon?
Answers
Approximately 11.21% of the racers did not complete the marathon.
To find the percentage of racers who did not complete the marathon, we need to calculate the ratio of the number of racers who did not complete (gave up or were disqualified) to the total number of racers who started the marathon.
The number of racers who did not complete the marathon is the sum of those who gave up and those who were disqualified, which is 29 + 8 = 37.
So, the percentage of racers who did not complete the marathon is given by:
(37 / 330) * 100
Calculating this expression:
(37 / 330) * 100 ≈ 11.21%
Therefore, approximately 11.21% of the racers did not complete the marathon.
To learn more about percentage visit:
brainly.com/question/32575737
#SPJ11
A cone has a radius of 4 centimeters and a height of 9 centimeters. Describe how the change affects the volume of the cone.
b. The radius is doubled.
Answers
In this particular scenario, if the height of the cone is doubled while the radius remains the same, the volume of the cone will be doubled as well.
The volume of a cone can be calculated using the formula V = (1/3)πr²h, where V represents the volume, r is the radius, and h is the height of the cone.
In the given scenario, the cone has a radius of 4 centimeters and a height of 9 centimeters. If we consider the initial volume of the cone as V₁, we can calculate it using the formula: V₁ = (1/3)π(4²)(9) = (1/3)π(16)(9) = 48π cm³.
Now, let's consider the situation where the height is doubled. In this case, the new height would be 2 times the original height, which is 2(9) = 18 centimeters. Let's denote the new volume of the cone as V₂. Using the formula, we can calculate it as follows: V₂ = (1/3)π(4²)(18) = (1/3)π(16)(18) = 96π cm³.
Comparing the two volumes, we have V₂ = 96π cm³ and V₁ = 48π cm³. The ratio of V₂ to V₁ is 96π/48π = 2. This indicates that the volume of the cone is indeed doubled when the height is doubled.
learn more about volume here:
https://brainly.com/question/29767724
#SPJ11
Hehehehehehehehheheheh
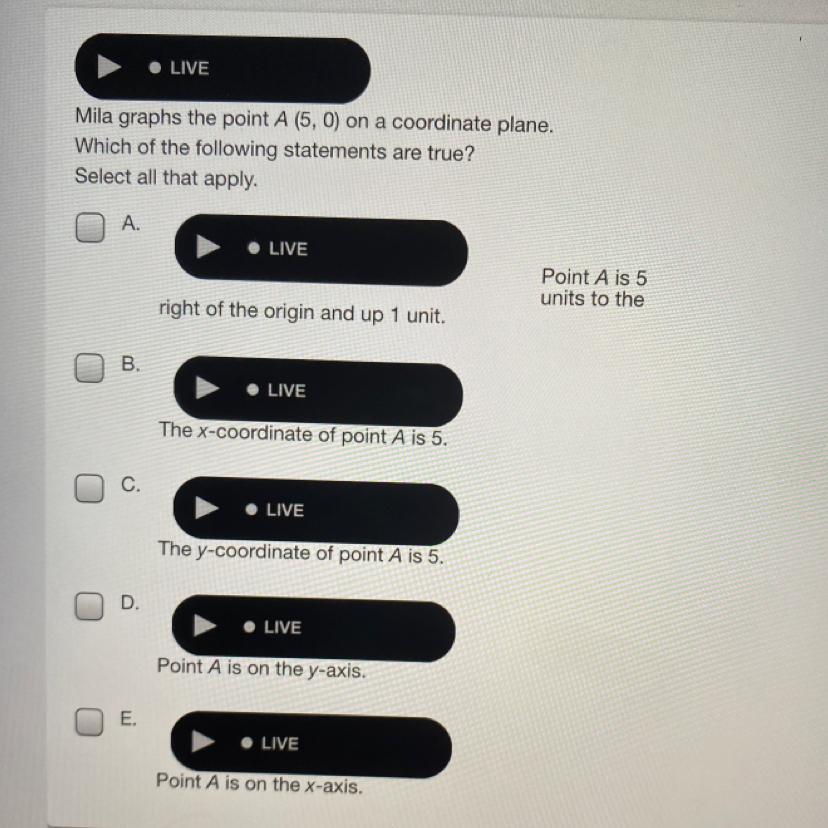
Answers
Answer:
B, E
Step-by-step explanation:
A would be wrong because the second part (up 1) would give you (5,1) The origin is (0,0)
B is correct because (5,0) has a 5 as the x coordinate
C is wrong because the y coordinate is 0
D is wrong because A is on the x since the y coordinate is 0
E is correct because (5,0) has a 5 on the x and a 0 on the y
What’s the radius of center (-2,1) and contains the point (2,-1)
Answers
To find the radius of a circle when we're given the coordinates of its center and a point it contains, we can use the following formula for distance:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2\)
\((x_1,y_1)\) is one point and \((x_2,y_2)\) is anotherSolving the QuestionWe're given:
Center: (-2,1)Point: (2,-1)Plug these given points into the formula for distance:
\(d=\sqrt{(2-(-2))^2+(-1-1)^2}\\d=\sqrt{(2+2)^2+(-1-1)^2}\\d=\sqrt{(4)^2+(-2)^2}\\d=\sqrt{16+4}\\d=\sqrt{20}\\d\approx4.47\)
AnswerTherefore, the radius of the circle is \(\sqrt{20}\) units, or approximately 4.47 units.
A rectangle is 40 yards long and 30 yards wide. What is the length of the diagonal that cuts through the center?
Answers
Answer:
it should be 50
Step-by-step explanation:
Using the pythagorean theorem c = \(\sqrt{a^{2} +b^{2} }\) we get 50
The value of 5^-3x2^-1
Answers
Answer:
Step-by-step explanation:
=5^-3 X 2^-1
= 1/5³ X 1/2
=1/(5³X 2)
=1/250 (Answer)
OR
=0•004 (Answer)
Answer:
1/250 or 0.004.
Step-by-step explanation:
5^-3 x 2^-1
= 1/5^3 * 1/2
= 1/125 * 1/2
= 1/250.
a rectangle is inscribed with its base on the x-axis and its upper corners on the parabola 6-x^2 . what are the dimensions of such a rectangle with the greatest possible area?
Answers
The dimensions of the rectangle with the greatest possible area are 2\(\sqrt{(2)}\) by 4.
Let's denote the dimensions of the rectangle as length (L) and width (W). Since the base of the rectangle is on the x-axis, the width of the rectangle is equal to the x-coordinate of the upper corners of the rectangle.
Let's assume that the x-coordinate of the upper corners of the rectangle is x. Then, the width of the rectangle is W = 2x, and the length of the rectangle is L = 6 -\(x^2\).
The area of the rectangle is A = LW = \(2x(6 - x^2) = 12x - 2x^3.\)
To find the maximum area, we need to take the derivative of A with respect to x and set it equal to zero:
\(dA/dx = 12 - 6x^2 = 0\)
Solving for x, we get:
x = ±sqrt(2)
Since we are interested in the dimensions of the rectangle on the parabola, we take the positive value of x.
Therefore, the width of the rectangle is:
W = 2x = 2sqrt(2)
And the length of the rectangle is:
L = 6 - \(x^2\)= 6 - 2 = 4
So the dimensions of the rectangle with the greatest possible area are 2sqrt(2) by 4.
To learn more about dimensions visit: https://brainly.com/question/28688567
#SPJ11
The population of a city is P(t)=9e "
P(t)=9 e^{0.05 t} (in millions), where t is measured in years. (a) Calculate the doubling time of the population. (b) How long does it take for the population to triple in size? (c) How long does it take for the population to quadruple in size? (a) (b) (c)
Answers
(a) The doubling time of the population is approximately 13.86 years., (b) It takes approximately 23.10 years for the population to triple in size, (c) It takes approximately 27.72 years for the population to quadruple in size.
To calculate the doubling time of the population, we need to find the time it takes for the population to double from its initial value. In this case, the initial population is 9 million.
(a) Doubling Time:
Let's set up an equation to find the doubling time. We know that when the population doubles, it will be 2 times the initial population.
2P(0) = P(t)
Substituting P(t) = 9e^(0.05t), we have:
2 * 9 = 9e^(0.05t)
Dividing both sides by 9:
2 = e^(0.05t)
To solve for t, we take the natural logarithm (ln) of both sides:
ln(2) = 0.05t
Now, we can isolate t by dividing both sides by 0.05:
t = ln(2) / 0.05
Using a calculator, we find:
t ≈ 13.86
Therefore, the doubling time of the population is approximately 13.86 years.
(b) Time to Triple the Population:
Similar to the doubling time, we need to find the time it takes for the population to triple from its initial value.
3P(0) = P(t)
3 * 9 = 9e^(0.05t)
Dividing both sides by 9:
3 = e^(0.05t)
Taking the natural logarithm of both sides:
ln(3) = 0.05t
Isolating t:
t = ln(3) / 0.05
Using a calculator, we find:
t ≈ 23.10
Therefore, it takes approximately 23.10 years for the population to triple in size.
(c) Time to Quadruple the Population:
Similarly, we need to find the time it takes for the population to quadruple from its initial value.
4P(0) = P(t)
4 * 9 = 9e^(0.05t)
Dividing both sides by 9:
4 = e^(0.05t)
Taking the natural logarithm of both sides:
ln(4) = 0.05t
Isolating t:
t = ln(4) / 0.05
Using a calculator, we find:
t ≈ 27.72
Therefore, it takes approximately 27.72 years for the population to quadruple in size.
Learn more about logarithm at: brainly.com/question/30226560
#SPJ11
Maria baked x cookies. She distributed the
cookies equally among her 6 neighbors.
Each neighbor received 18 cookies. Which
equation matches this situation?
Answers
Answer: She baked 108 cookies!
Step-by-step explanation: I did : (6x8) and it gave me (108) and too check my answer i did (108 divided my 6) it gave me 18.
PLZ HELP IN QUIZ NOW
3. Solve this equation with a variable term on both sides: 4y + 10 = 3y – 8 What is the solution?
Answers
Answer:
4y+10=-5
4y=-5-10
4y=-15
y=-15/4
y=3.25
Geometry 6.2
What is m∠N

Answers
Check the picture below.
Solve the 1 st order linear DEQ for x in (0,[infinity]). dy/dx + 2/x y=x
Answers
The solution to the first-order linear differential equation dy/dx + (2/x)y = x, where x is in the interval (0, ∞), is given by y = (C/\(x^{2}\)) + (x/3), where C is an arbitrary constant.
To solve the given differential equation, we'll use the method of integrating factors. First, we rewrite the equation in standard form by dividing both sides by x:
dy/dx + (2/x)y = 1.
The integrating factor is determined by multiplying both sides of the equation by the exponential of the integral of the coefficient of y, which in this case is (2/x):
I.F. =\(e^(\int(2/x)dx)\) = \(e^{(2ln|x|)}\) =\(e^{(ln|x^2|)}\) = \(x^{2}\).
Multiplying both sides of the equation by the integrating factor, we have:
\(x^{2}\)(dy/dx) + 2xy = \(x^3\).
Notice that the left-hand side can be expressed as the derivative of the product\(x^2\)y with respect to x. Applying the product rule, we get:
d/dx(\(x^{2}\)y) = \(x^3\).
Integrating both sides with respect to x, we obtain:
\(x^{2}\)y = (1/4)\(x^4\) + C,
where C is the constant of integration. Dividing through by \(x^{2}\), we get:
y = (1/4)\(x^{2}\) + C/\(x^{2}\).
Since x is in the interval (0, ∞), the term C/\(x^{2}\) approaches zero as x approaches infinity, resulting in the final solution:
y = (1/4)\(x^{2}\)+ (C/\(x^{2}\)).
To satisfy the initial condition, we need to determine the value of the constant C.
Learn more about first-order linear differential equation here:
https://brainly.com/question/32514979
#SPJ11