find the radius of convergence, r, of the following series. [infinity] n!(2x − 1)n n = 1 r = find the interval, i, of convergence of the series.
Answers
The series is given by `[infinity] n!(2x − 1)^n n = 1`In order to find the radius of convergence of the given series, we need to use the ratio test.
The ratio test states that the series `∑an` converges if the limit `limn→∞ |an+1/an| < 1`, and diverges if the limit `limn→∞ |an+1/an| > 1`. If the limit is equal to 1, then the test is inconclusive. Using the ratio test,
we have: `limn→∞ |(n + 1)! (2x - 1)^(n + 1) / n! (2x - 1)^n|`=`limn→∞ |(n + 1) (2x - 1)|`
=`2x - 1`
Therefore, the series converges for `|2x - 1| < 1`, and diverges for `|2x - 1| > 1`.
If `|2x - 1| = 1`, then the test is inconclusive. So, the radius of convergence, `r`, is 1, and the interval of convergence, `I`, is given by: `I = {x : |2x - 1| < 1}
= {(x : -1/2 < x < 3/2}`.
Hence, the radius of convergence is 1 and the interval of convergence is (-1/2, 3/2).
To know more about convergence visit:
https://brainly.com/question/29258536
#SPJ11
Related Questions
From a hot-air balloon, Violet measures a 27^{\circ} ∘ angle of depression to a landmark that’s 790 feet away, measuring horizontally. What’s the balloon’s vertical distance above the ground? Round your answer to the nearest tenth of a foot if necessary.
Answers
The balloon’s vertical distance above the ground is 402.53 ft
How to solve for the vertical distanceTwo legs of a right triangle are formed by the horizontal and the vertical. The tangent relation is applicable because the provided angle is the angle next to the horizontal leg:
TOA = Tangent Opposite Adjacent
Tangent = opposite / adjacent
cross multiply
opposite = tan * adjacent
The tangent is 27 degrees
The adjacent is 790 feet away
= tan 27 degrees * 790
= 402.53
This balloon can be said to be 402.53 ft above the ground.
Read more on distance here: https://brainly.com/question/24834665
#SPJ1
Answer:
402.5
Step-by-step explanation:
I got the question right
Parallel and transversals

Answers
I was in a rush so I couldn't write fown the steps. If you need the explanations for how they were gotten, please say.

What is 2 divided by 3? Explain the steps pleas.
Answers
The value of 2 divided by 3 is 0.67
How to evaluate the quotient expression?From the question, we have the following parameters that can be used in our computation:
2 divided by 3
To start with, we need to represent the expression properly as a quotient
So, we have the following representation
2 divided by 3 = 2/3
Evaluate the quotient expression using a calculator
This gives
2 divided by 3 = 0.67
Hence, the solution to 2 divided by 3 is 0.67
Read more about quotient expressions at
https://brainly.com/question/1807180
#SPJ1
i need help its due tonight! Thank you so much to whoever helps!

Answers
⇒To check if the given point (2,-8) is the solution to the system you should have a general knowledge that 2 is the input that is represented by variable x and -8 is the output variable represented by letter y.
⇒Now to check if the point is a solution we will have to check for both cases ....y<x-1 and .....y>-x+2
x=2 and y=-8 in the system y< x-1
LHS=-8
RHS=(2)-1
RHS=1
-8<1
The result is true for the first inequality
for the second system inequality
x=2 and y=-8
LHS=-8
RHS=-(2)+2
RHS=-2+2
RHS=0
-8<0 but in the inequality it is saying that -8>0 which is not true but False
⇒As a conclusion point (2,-8) is not a solution to the system as it does not apply to both the conditions.
⇒The answer is no.
Find the surface area of the solid formed by the net.

Answers
Answer:
Step-by-step explanation:
m
Answer:
535.44 cm squared
Step-by-step explanation:
Solve the following maximisation problem by applying the Kuhn-Tucker theorem: Max xy subject to –4x^2 – 2xy – 4y^2 x + 2y ≤ 2 2x - y ≤ -1
Answers
By applying the Kuhn-Tucker theorem, the maximum value of xy is: 18/25
The constraints are:-4x² - 2xy - 4y²x + 2y ≤ 22x - y ≤ -1
Let us solve this problem by applying the Kuhn-Tucker theorem.
Let us first write down the Lagrangian function:
L = xy + λ₁(-4x² - 2xy - 4y²x + 2y - 2) + λ₂(2x - y + 1)
Then, we find the first order conditions for a maximum:
Lx = y - 8λ₁x - 2λ₁y + 2λ₂ = 0
Ly = x - 8λ₁y - 2λ₁x = 0
Lλ₁ = -4x² - 2xy - 4y²x + 2y - 2 = 0
Lλ₂ = 2x - y + 1 = 0
The complementary slackness conditions are:
λ₁(-4x² - 2xy - 4y²x + 2y - 2) = 0
λ₂(2x - y + 1) = 0
Now, we solve for the above equations one by one:
From equation (3), we can write 2x - y + 1 = 0, which implies:y = 2x + 1
Substitute this in equation (1), we get:
8λ₁x + 2λ₁(2x + 1) - 2λ₂ - x = 0
Simplifying, we get:
10λ₁x + 2λ₁ - 2λ₂ = 0 ... (4)
From equation (2), we can write x = 8λ₁y + 2λ₁x
Substitute this in equation (1), we get:
8λ₁(8λ₁y + 2λ₁x)y + 2λ₁y - 2λ₂ - 8λ₁y - 2λ₁x = 0
Simplifying, we get:
-64λ₁²y² + (16λ₁² - 10λ₁)y - 2λ₂ = 0 ... (5)
Solving equations (4) and (5) for λ₁ and λ₂, we get:
λ₁ = 1/20 and λ₂ = 9/100
Then, substituting these values in the first order conditions, we get:
x = 2/5 and y = 9/5
Therefore, the maximum value of xy is:
2/5 x 9/5 = 18/25
Hence, the required answer is 18/25.
Learn more about Lagrangian function at:
https://brainly.com/question/13314103
#SPJ11
A sequence of numbers follows the rule: multiply the previous number by -2 and add 3. the forth term in the sequence is -7
Answers
please help me with this

Answers
Answer:
Y=MX+C is the equations of a straight line where C is the constant (y intercept)
Looking at a and b and the two graphs c and d
The function c represents the lowest value of the y intercept which is at -3
a boat travels for three hours with a current of 3 mph and then returns the same distance in 4 hours. what is the boat's speed in calm water and how for did the boat travel 1 way?
Answers
The boat's speed in calm water is approximately 5.57 mph and it traveled approximately 14.57 miles in one direction.
Let's denote the speed of the boat in calm water as $b$ (in mph) and the distance it traveled in one direction as $d$ (in miles).
When traveling with the current, the effective speed of the boat is $b+3$, and when traveling against the current, the effective speed is $b-3$. We can use the formula:
distance
=
speed
×
time
distance=speed×time
to set up two equations based on the distances traveled:
�
=
3
(
�
+
3
)
(with the current)
d=3(b+3)(with the current)
�
=
4
(
�
−
3
)
(against the current)
d=4(b−3)(against the current)
We can simplify these equations to:
3
�
+
9
=
4
3
(
�
+
9
)
(with the current)
3b+9=
3
4
(d+9)(with the current)
4
�
−
12
=
�
(against the current)
4b−12=d(against the current)
Now we can solve this system of equations for $b$ and $d$.
Starting with the second equation, we can isolate $d$:
�
=
4
�
−
12
d=4b−12
Substituting this into the first equation:
3
�
+
9
=
4
3
(
4
�
−
12
+
9
)
3b+9=
3
4
(4b−12+9)
Simplifying and solving for $b$:
3
�
+
9
=
4
3
(
4
�
−
3
)
3b+9=
3
4
(4b−3)
9
�
+
27
=
16
�
−
12
9b+27=16b−12
7
�
=
39
7b=39
�
=
39
7
≈
5.57
mph
b=
7
39
≈5.57 mph
Now we can use either equation to find $d$. Let's use the second equation:
�
=
4
�
−
12
=
4
(
39
7
)
−
12
≈
14.57
miles
d=4b−12=4(
7
39
)−12≈14.57 miles
Learn more about speed at: brainly.com/question/17661499
#SPJ11
PLEASE HELP IM SERIOUSLY STUCK

Answers
Formula for the Slope: (y2 - y1) / (x2 - x1)
You can use any two points to find the slope, as long as those two points are on the line.
Point 1 = (-2, 8)
Point 2 = (0, 0)
Slope = (0 - 8) / (0 - - 2)
Slope = -8 / 2
Slope = -4
Hope this helps!
Answer:
-4
Step-by-step explanation:
The formula to find the slope is (change in y)/(change in x). In other words, rise over run.
If we look at the data, we can see that the x and y value changes.
x value: -3 --> -2 --> -1 --> 0 --> 1
y value: 12 --> 8 --> 4 --> 0 --> -4
When y changed from 12 to 8, the x changed from -3 to -2.
y: 12 --> 8
x: -3 --> -2
There was a difference of -4 in the y and a difference of 1 in the x.
At the top, I wrote that the slope was (change in y)/(change in x)
With -4 and 1 we found, we can say that the slope is -4/1.
If we simplify this answer, we end up with -4.
So -4 is the slope of the data.
Jameson pays $39.90 for 3.8 pounds of almonds. What is the price per pound of almonds?
Answers
Step-by-step explanation: The price of3.8 pounds of almonds=$39.90 thus we can write Hence the price of almonds is $10.50 per pounds.
AWNSERS:$10.50
Answer:
Step-by-step explanation: 39.90 x 3.8 = 151.62
Selina has $50. She wants to buy some donuts which cost $2.80 each. How many donuts can she buy?
Answers
Answer:
50/2.80= 17
17 dounuts
they only said simplify and i guessed the answer as undefined
Answers
(40 points) Consider a fishery that has a stock S with the following growth rate: G(S)=0.4S(1−
10000
S
);0≤S≤10000 Suppose that the harvest is a function of effort E as well as the stock S : H(E,S)=0.01ES. Further assume that the price of fish P=2 is constant, and total cost of effort is TC(E)=50E+E
2
(a) (10 points) Calculate the size of the biomass S
MSY
for the maximum sustainable yield (MSY). What is the corresponding effort level E
MSY
to get the maximum sustainable yield? (b) ( 10 points) Calculate the effort level E
OA
if there is open access to the fishery.
Answers
a) The effort level E MSY to get the maximum sustainable yield is 0.
b) The effort level E OA is not constrained.
(a) To calculate the size of the biomass S MSY for the maximum sustainable yield (MSY), we need to find the stock level where the growth rate G(S) is equal to the harvest rate H(E,S).
G(S) = H(E,S)
0.4S(1−10000/S) = 0.01ES
S(1−10000/S) = 0.01E
S - 10000 = 0.01E
S = 0.01E + 10000
To find S MSY , we need to set the growth rate G(S) equal to zero:
G(S) = 0.4S(1−10000/S) = 0
0.4S(1−10000/S) = 0
S(1−10000/S) = 0
S = 0 or S = 10000
Since S cannot be zero in this context, the size of the biomass S MSY for the maximum sustainable yield is 10,000.
To find the corresponding effort level E MSY , we substitute S MSY into the equation:
S = 0.01E + 10000
10000 = 0.01E + 10000
0.01E = 0
E MSY = 0
(b) In an open access fishery, there are no restrictions on the amount of effort that can be applied. Therefore, the effort level E OA is not constrained.
Know more about the growth rate
https://brainly.com/question/30611694
#SPJ11
Please help me with this question! Will mark brainliest :)

Answers
Answer:
Y=-2x + 5
Step-by-step explanation:
The line goes through the point (0,5) and the slope is -2.
y=-2x+5
The point passes through 0,5
. Determine the standard equation of the ellipse using the stated information.
Foci at (8,−1) and (−2,−1); length of the major axis is twelve units
The equation of the ellipse in standard form is _____.
b. Determine the standard equation of the ellipse using the stated information.
Vertices at (−5,12) and (−5,2); length of the minor axis is 8 units.
The standard form of the equation of this ellipse is _____.
c. Determine the standard equation of the ellipse using the stated information.
Center at (−4,1); vertex at (−4,10); focus at (−4,9)
The equation of the ellipse in standard form is ____.
Answers
a. The standard equation of the ellipse with foci at (8, -1) and (-2, -1), and a length of the major axis of 12 units is: ((x - 5)² / 6²) + ((y + 1)² / b²) = 1.
b. The standard equation of the ellipse with vertices at (-5, 12) and (-5, 2), and a length of the minor axis of 8 units is: ((x + 5)² / a²) + ((y - 7)² / 4²) = 1.
c. The standard equation of the ellipse with a center at (-4, 1), a vertex at (-4, 10), and a focus at (-4, 9) is: ((x + 4)² / b²) + ((y - 1)² / 9²) = 1.
a. To determine the standard equation of the ellipse with foci at (8, -1) and (-2, -1), and a length of the major axis of 12 units, we can start by finding the distance between the foci, which is equal to the length of the major axis.
Distance between the foci = 12 units
The distance between two points (x₁, y₁) and (x₂, y₂) is given by the formula:
√((x₂ - x₁)² + (y₂ - y₁)²)
Using this formula, we can calculate the distance between the foci:
√((8 - (-2))² + (-1 - (-1))²) = √(10²) = 10 units
Since the distance between the foci is equal to the length of the major axis, we can conclude that the major axis of the ellipse lies along the x-axis.
The center of the ellipse is the midpoint between the foci, which is (5, -1).
The equation of an ellipse with a center at (h, k), a major axis of length 2a along the x-axis, and a minor axis of length 2b along the y-axis is:
((x - h)² / a²) + ((y - k)² / b²) = 1
In this case, the center is (5, -1) and the major axis is 12 units, so a = 12/2 = 6.
Therefore, the equation of the ellipse in standard form is:
((x - 5)² / 6²) + ((y + 1)² / b²) = 1
b. To determine the standard equation of the ellipse with vertices at (-5, 12) and (-5, 2), and a length of the minor axis of 8 units, we can start by finding the distance between the vertices, which is equal to the length of the minor axis.
Distance between the vertices = 8 units
The distance between two points (x₁, y₁) and (x₂, y₂) is given by the formula:
√((x₂ - x₁)² + (y₂ - y₁)²)
Using this formula, we can calculate the distance between the vertices:
√((-5 - (-5))² + (12 - 2)²) = √(0² + 10²) = 10 units
Since the distance between the vertices is equal to the length of the minor axis, we can conclude that the minor axis of the ellipse lies along the y-axis.
The center of the ellipse is the midpoint between the vertices, which is (-5, 7).
The equation of an ellipse with a center at (h, k), a major axis of length 2a along the x-axis, and a minor axis of length 2b along the y-axis is:
((x - h)² / a²) + ((y - k)² / b²) = 1
In this case, the center is (-5, 7) and the minor axis is 8 units, so b = 8/2 = 4.
Therefore, the equation of the ellipse in standard form is:
((x + 5)² / a²) + ((y - 7)² / 4²) = 1
c. To determine the standard equation of the ellipse with a center at (-4, 1), a vertex at (-4, 10), and a focus at (-4, 9), we can observe that the major axis of the ellipse is vertical, along the y-axis.
The distance between the center and the vertex gives us the value of a, which is the distance from the center to either focus.
a = 10 - 1 = 9 units
The distance between the center and the focus gives us the value of c, which is the distance from the center to either focus.
c = 9 - 1 = 8 units
The equation of an ellipse with a center at (h, k), a major axis of length 2a along the y-axis, and a distance c from the center to either focus is:
((x - h)² / b²) + ((y - k)² / a²) = 1
In this case, the center is (-4, 1), so h = -4 and k = 1.
Therefore, the equation of the ellipse in standard form is:
((x + 4)² / b²) + ((y - 1)² / 9²) = 1
To learn more about standard equation of the ellipse visit : https://brainly.com/question/29187531
#SPJ11
14. A surveyor observes that the top of a building makes an angle of 32° with the road.From another location 300 ft. from the base of the building, the angle of elevation is 22°How far is the base of the building from the first observation point, ×, on the road?

Answers
Considering h as the height of the building, we have the following set of relations for a right triangle:
\(\begin{gathered} 300\cdot x=h^2 \\ h=300\cdot\tan22\degree \\ h\approx121\text{ ft} \\ \therefore x=\frac{121^2}{300}\approx49\text{ ft} \end{gathered}\)Simplify the expression.
2.4-5.4n3n+6
...
2.4-5.4n-3n+6=
(Simplify your answer. Use integers or decimals for any numbers in the expression.)
Answers
Answer:
8.4-16.2n²
Step-by-step explanation:
2.4-5.4n3n+6
= 2.4-16.2n²+6
= 8.4-16.2n²
PLEASE HELP MAX POINTS AND BRAINLIEST!!!
(04.03 MC)
A biologist is studying the growth of a particular species of algae. She writes the following equation to show the radius of the algae, f(d), in mm, after d days:
f(d) = 7(1.06)d
Part A: When the biologist concluded her study, the radius of the algae was approximately 13.29 mm. What is a reasonable domain to plot the growth function? (4 points)
Part B: What does the y-intercept of the graph of the function f(d) represent? (2 points)
Part C: What is the average rate of change of the function f(d) from d = 4 to d = 11, and what does it represent? (4 points)
Answers
#1
As d is days
So days can't be negative
hence domain is W or Whole numbers set.
But according to the equation
y=7(1.06)^d13.29=7(1.06)^d1.06^d=1.898dln1.06=ln1.898d=1.79Round to next whole as it's no of days
d=2
Domain=[2,oo)
#b
Put d=0
f(0)
7(1.06)^(0)7It passes through (0,7)
But 0 is not in domain ,hence no y intercept in real
#C
f(11)
7(1.06)¹¹13.28f(4)
7(1.06)⁴8.83Rate of change
f(11)-f(4)/11-413.28-8.83/70.6It represents change in radius
NEED ANSWER ASAP
Brad’s checking account starts off with a balance of $126.50. Throughout the week, Brad pays a bill for $87.21 and pays $5.64 for breakfast. He deposits $15.00 but then pays another bill for $55.25. At the end of the week, he gets a notice from the bank that he has a negative balance. How much does Brad need to deposit into his account to get to a $0 balance?
Answers
Answer:
$6.60
Step-by-step explanation:
Answer:
$6.6
Step-by-step explanation:
We add the amount he paid,
($87.21 + $5.64) - $15.00 + 55.25
We will get ,
$92.85 - $15.00 + $55.25
Then,
$77.85 + $55.25
We will get,
$133.10, the subtract the $133.10 from his original balance and get
$126.50 - $133.10 = $-6.6
He will need to deposit $6.6 to get his account to $0 balance
Is 1over9 > or < 1over11

Answers
The fraction 1/9 is greater than the fraction 1/11.
How to compare fractions?Comparing fractions involves a set of rules related to the numerator and the denominator. When any two fractions are compared, we get to know the greater and the smaller fraction.
To compare unlike fractions:
Step 1: Observe the denominators of the given fractions: .
Step 2: Now, let us convert them in such a way that the denominators become the same.
Step 3: Compare the fractions:
Step 4: The fraction with the larger numerator is the larger fraction.
The given fractions are 1/9 and 1/11.
Here, LCM of denominator 9 and 11 is 99
Then, fractions becomes 11/99 and 9/99
11/99>9/99
1/9>1/11
Therefore, the fraction 1/9 is greater than the fraction 1/11.
Learn more about the comparison of fractions here:
https://brainly.com/question/12686260.
#SPJ1
Which expression is equivalent to
i need help asap

Answers
There plz help me I still have one more

Answers
Answer:
D.
5/5 is basically 1 whole number :)
find the area of the region bounded. y the curve y=f(x)=x^3-4x 1 and the tangent line to the curve y=f(x) at (-1,4)
Answers
Therefore, the area of the region bounded by the curve \(y = f(x) = x^3 - 4x + 1\) and the tangent line y = -x + 3 at (-1,4) is -3/4 square units.
To find the area of the region bounded by the curve \(y = f(x) = x^3 - 4x + 1\) and the tangent line to the curve at (-1,4), we need to determine the points of intersection between the curve and the tangent line.
First, let's find the equation of the tangent line. The tangent line at (-1,4) has the same slope as the derivative of f(x) at x = -1. Let's find this derivative: \(f'(x) = 3x^2 - 4\).
Evaluating the derivative at x = -1:
\(f'(-1) = 3(-1)^2 - 4 = 3 - 4 = -1.\).
Therefore, the slope of the tangent line is -1.
Using the point-slope form of a line, the equation of the tangent line is: y - 4 = -1(x + 1).
Simplifying, we get: y = -x + 3.
Next, we find the points of intersection by setting the curve equation and the tangent line equation equal to each other: \(x^3 - 4x + 1 = -x + 3\).
Rearranging and simplifying, we get:\(x^3 - 3x + 2 = 0\).
Factoring the equation, we find that x = -1 is a root: \((x + 1)(x^2 - x + 2) = 0\)
The quadratic term \(x^2 - x + 2\) has no real roots, so the only intersection point is (-1, 4).
Now, we can find the area of the region bounded by the curve and the tangent line by calculating the definite integral of the positive difference between the curve and the line over the interval from x = -1 to x = 0:
Area = ∫[-1,0] [f(x) - (-x + 3)] dx.
Let's find this integral:
Area = ∫[-1,0] (\(x^3 - 4x + 1 + x - 3\)) dx = ∫[-1,0] (\(x^3 - 3x - 2\)) dx.
Integrating term by term:
\(Area = [\frac{1}{4} x^4 - \frac{3}{2} x^2 - 2x] |[-1,0]\)
\(= [\frac{1}{4} (0)^4 - \frac{3}{2} (0)^2 - 2(0)] - [\frac{1}{4} (-1)^4 - \frac{3}{2} (-1)^2 - 2(-1)]\)
\(= 0 - [\frac{-1}{4} - \frac{3}{2} + 2]\)
\(= -\frac{1}{4} + \frac{3}{2} - 2\)
\(= -\frac{1}{4} + \frac{6}{4} - \frac{8}{4}\)
\(= -\frac{3}{4}\)
Therefore, the area of the region bounded by the curve \(y = f(x) = x^3 - 4x + 1\) and the tangent line y = -x + 3 at (-1,4) is -3/4 square units.
To know more about "Tagent" refer here:
https://brainly.com/question/32033477#
#SPJ11
Change each phrase into an algebraic expression
Answers
Answer:
When translating phrases into algebraic expressions, you need to identify keywords and phrases which specifically refer to a mathematical operation (addition, subtraction, multiplication, and division). Usually, you can write out the algebraic expression of the verbal description in the order that it is said
Normalize the following vectors.a) u=15i-6j +8k, v= pi i +7j-kb) u=5j-i , v= -j + ic) u= 7i- j+ 4k , v= i+j-k
Answers
The normalized vector is:
V\(_{hat}\) = v / |v| = (1/√3)i + (1/√3)j - (1/√3)k
What is algebra?Algebra is a branch of mathematics that deals with mathematical operations and symbols used to represent numbers and quantities in equations and formulas.
a) To normalize the vector u = 15i - 6j + 8k, we need to divide it by its magnitude:
|u| = sqrt(15² + (-6)² + 8²) = sqrt(325)
So, the normalized vector is:
\(u_{hat}\) = u / |u| = (15/√325)i - (6/√325)j + (8/√325)k
Similarly, to normalize the vector v = pi i + 7j - kb, we need to divide it by its magnitude:
|v| = √(π)² + 7² + (-1)²) = √(p² + 50)
So, the normalized vector is:
\(V_{hat}\) = v / |v| = (π/√(p² + 50))i + (7/√(p² + 50))j - (1/√(p² + 50))k
b) To normalize the vector u = 5j - i, we need to divide it by its magnitude:
|u| = √(5² + (-1)²) = √(26)
So, the normalized vector is:
\(u_{hat}\) = u / |u| = (5/√(26))j - (1/√(26))i
Similarly, to normalize the vector v = -j + ic, we need to divide it by its magnitude:
|v| = √(-1)² + c²) = √(c² + 1)
So, the normalized vector is:
\(V_{hat}\) = v / |v| = - (1/√(c² + 1))j + (c/√(c² + 1))i
c) To normalize the vector u = 7i - j + 4k, we need to divide it by its magnitude:
|u| = √(7² + (-1)² + 4²) = √(66)
So, the normalized vector is:
\(u_{hat}\) = u / |u| = (7/√(66))i - (1/√(66))j + (4/√(66))k
Similarly, to normalize the vector v = i + j - k, we need to divide it by its magnitude:
|v| = √(1² + 1² + (-1)²) = √(3)
So, the normalized vector is:
\(V_{hat}\) = v / |v| = (1/√(3))i + (1/√(3))j - (1/√(3))k
To learn more about Algebra from the given link:
https://brainly.com/question/24875240
#SPJ4
The graph below represents the solution set of which inequality?
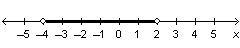
Answers
Answer:
x < 2
Step-by-step explanation:
The indicated part is left from point 2.
You see an open circle at point (2,0) which means you should exclude the point x = 2 in the inequation.
Now you have enough info to get the right inequality:
x < 2
The figure(Figure 1) is a graph of Ex. The potential at the origin is -140 V . What is the potential at x=3.0m? Expert Answer. Who are the experts?
Answers
As per the given origin, the potential at x = 3.0m is 143.0V
The term origin in math is referred as the initial point or the starting point from where we begin our calculations or measurements.
Here we have given that the potential at the origin is -140 V.
And we need to find the potential at x = 3.0m.
While we looking into the given question, we have identified that the region of space has a non-uniform electric field that points in the +x-direction and has magnitude and as the reference point, it take the potential at the origin to be -140 V .
Then the electric potential at x=3.0m is calculated as,
=> V(3) - 140 = 3.0
=> V(3) = 143.0
To know more about origin here.
https://brainly.com/question/17963034
#SPJ4
2.
Which situation represents a non-proportional relationship?
The cost of purchasing p pounds of salmon for $7.99 per pound.
The amount a student makes mowing m number of lawns charging $35 per lawn.
The amount of water draining at a rate of 2.5 gallons per minute.
The total cost of renting a jet ski for $25 per hour plus a fee of $50.
Answers
Answer: The amount of water draining at a rate of 2.5 gallons per minute.
Step-by-step explanation: A non-proportional relationship is when the slope passes through the origin. A non-proportional relationship does NOT have a fee.
John spent 80% of his money and saved the rest. Peter spent 75% of his money and saved the rest. If they saved the same amount of money, what is the ratio of John’s money to Peter’s money? Express your answer in its simplest form.
Answers
The ratio of John's money to Peter's money is 5/4. This means if John has a total amount of 5 then Peter will have a total of 4 as his amount.
Let's assume John has 'x' amount of money, Peter has 'y' amount of money, The money John saved is 'p' and the money Peter saved is 'q'
So,
p = x - 80x/100 (equation 1)
q = y - 75y/100 (equation 2)
According to the given question, the amount John saved is equal to the amount Peter saved. Hence, we can equate equations 1 and 2.
p = q
x- 80x/100 = y - 75y/100
x - 0.8x = y - 0.75y
0.2x = 0.25y
x = 0.25y/0.2
x/y = 0.25/0.2
x/y = 25/20
x/y = 5/4
Hence, the ratio of John's money to Peter's money is 5/4.
To learn more about Ratio:
https://brainly.com/question/13419413