Find the product.
y4 · y6
Answers
The answer is \(y^{4+6}\) = \(y^{10}\)
Related Questions
The National Collegiate Athletic Association (NCAA) requires colleges to report the graduation rates of their athletes. At one large university, 91% of all students who started their studies in 2000-2010 graduated within 6 years. A sports reporter contacted 152 athletes randomly sampled from that same university and time period and found that 132 of them had graduated within 6 years.
(a) (5 points) Perform the appropriate hypothesis test to determine whether this is significant evidence that the percentage of athletes who graduate is less than for the student population at large, using the significance level a = 0.05. Remember for state the null and alternative hypotheses, the decision rule, and your conclusion.
(b) (3 points) Calculate the P-value for this test. Explain how this P-value can be use to test the hypotheses in part (a).
Answers
Answer:
a)
The null hypothesis is \(H_0: p = 0.91\).
The alternate hypothesis is \(H_1: p < 0.91\).
The decision rule is: accept the null hypothesis for \(z > -1.645\), reject the null hypothesis for \(z < -1.645\).
Since \(z = -1.79 < -1.645\), we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
b)
The p-value for this test is 0.0367. Since this p-value is less than the significance level of \(\alpha = 0.05\), we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
Step-by-step explanation:
Question a:
Perform the appropriate hypothesis test to determine whether this is significant evidence that the percentage of athletes who graduate is less than for the student population at large:
At the null hypothesis, we test if the proportion is the same as the student population, of 91%. Thus:
\(H_0: p = 0.91\)
At the alternate hypothesis, we test that the proportion for athletes is less than 91%, that is:
\(H_1: p < 0.91\)
The test statistic is:
\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis, \(\sigma\) is the standard deviation and n is the size of the sample.
Test if the proportion is less at the 0.05 level:
The critical value is z with a p-value of 0.05, that is, z = -1.645. Thus, the decision rule is: accept the null hypothesis for \(z > -1.645\), reject the null hypothesis for \(z < -1.645\).
0.91 is tested at the null hypothesis:
This means that \(\mu = 0.91, \sigma = \sqrt{0.91*0.09}\)
A sports reporter contacted 152 athletes randomly sampled from that same university and time period and found that 132 of them had graduated within 6 years.
This means that \(n = 152, X = \frac{132}{152} = 0.8684\)
Value of the test statistic:
\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
\(z = \frac{0.8684 - 0.91}{\frac{\sqrt{0.91*0.09}}{\sqrt{152}}}\)
\(z = -1.79\)
Since \(z = -1.79 < -1.645\), we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
(b) (3 points) Calculate the P-value for this test. Explain how this P-value can be use to test the hypotheses in part (a).
The p-value of the test is the probability of finding a sample proportion of 0.8684 or below. This is the p-value of z = -1.79.
Looking a the z-table, z = -1.79 has a p-value of 0.0367.
The p-value for this test is 0.0367. Since this p-value is less than the significance level of \(\alpha = 0.05\), we reject the null hypothesis and accept the alternate hypothesis that that percentage of athletes who graduate is less than for the student population at large.
help me please
dont even need a full explanation

Answers
5x + 10 = 3x + 5
5x - 3x = 5 - 10
2x = -5
X = -5/2
What would the interval increasing and decreasing be? It’s for my math practice!
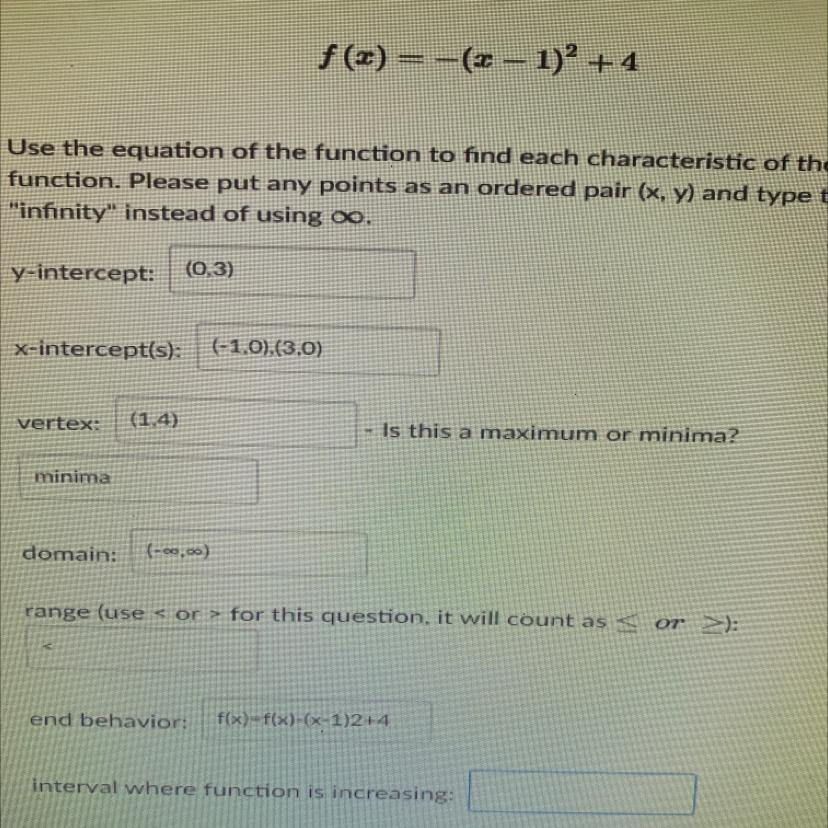
Answers
Answer:
-∞ < x < 1
Explanation:
The equation f(x) = -(x - 1)² + 4 is a parabola that opens down with vertex in the point (1, 4).
This is because it has the form:
f(x) = a(x - h)² + k
Where the sign of a says if it opens up or down and (h, k) is the vertex.
Since the parabola opens down, it will be increasing until the vertex point and then it will be decreasing. The vertex point is (x, y) = (1, 4). So the interval where the function is increasing is: -∞ < x < 1
Is the codomain of the transformation X -> ax the set of all linear combinations of the columns A?
Answers
No, the codomain of the transformation X -> AX (where A is a matrix) is the set of all linear combinations of A's columns, but it is not always the same as the set of all linear combinations of A's columns.
The codomain of a transformation X -> axe is the set of all possible transformation outputs, where X is a vector in vector space and an is a matrix.
If a represents a linear transformation, the transformation X -> axe maps a vector X to another vector that is the product of a and X.
In general, the codomain of the transformation X -> axe does not have to be the set of all linear combinations of a's columns. The codomain of X -> axe is simply the set of all vectors in the same vector space as X that are expressible as linear combinations of a's columns.
To learn more about linear combinations
https://brainly.com/question/30130774
#SPJ4
What point would represent the time it took to walk 7 1/2 miles?
Answers
Answer:
Miles walked 7 time 2.5 hours
A plant is already 41 centimeters tall, and it will grow one centimeter every month. The plant's height, H (in centimeters), AFTER M monthsis given by the following function H)M)=41+M WHat is the plants height after 12 the following function ,
Answers
The height of plant after 12 months be 53 centimeters.
What is meant by the term linear equation?A linear equation is just an algebraic equation of a form y=mx+b, where m is the slope while b is the y-intercept, and only a constant and first-order (linear) term are included. The variables in the preceding equation are y and x, and it is occasionally referred to as a "linear equation of two variables."For the stated question,
The height of plant is modeled by the equation-
H(M) = 41 + M
Plant's height, H (in centimeters),
M = month
initial height of plant = 41 centimeters
Thus, the plant's height after 12 months.
Put M = 12
H(M) = 41 + M
H(12) = 41 + 12
H(12) = 53 centimeters
Thus, the height of the plant after 12 months be 53 centimeters.
To know more about the linear equation, here
https://brainly.com/question/2030026
#SPJ1
Use technology to find the line of best fit for the following data. (−7,1), (2,9), (0,7), (−3,5), (−8,−2), (−1,2), (−6,−1), (−5,0), (0,5), (1,7), (−4,2), (3,7) When the equation of the line is in the form y=mx+b, what is the value of m?Enter your answer as a decimal rounded to the nearest tenths place, like this: 42.5Click on the following link to use the GeoGebra graphing calculator.

Answers
Given:
We have given so many values for line
Required:
To find the line for data
Explanation:
(-7,1) ,(2,9), (0,7), (-3,5) ,(-8,-2) , (-1,2)
(-6,-1), (-5,0), (0,5), (1,7), (-4,2), (3,7)
Using the online regression calculator:
slope
\(\begin{gathered} slope\text{ =0.8700}\pm0.1382 \\ y\text{ intercept= 5.613}\pm0.5837 \\ x\text{ intercept =-6.452} \\ \frac{1}{slope}=1.149 \end{gathered}\)Y- is the predictor variable
X- is the independent variable
5.613 =slope of gradient
0.5837= intercept (b) where the line best fit cross the y-axis
Required answer:
Above calculation
Despite the sizes of the two triangles, what do you notice about the ratios of each corresponding pair of sides in ΔABC and ΔADE?
Answers
Answer:
For each corresponding pair of sides, the ratios for the two triangles are equal.
Step-by-step explanation:
plato
Answer:
Sample answer for Edmentum and Plato
Like and Rate!

1. Determine the volume of the rectangular prism in two different ways.
3/4 ft
3/8ft
3/4ft
Answers
By first method, he volume of the rectangular prism is (9/32) cubic feet.
By second method, the volume of the rectangular prism is (27/64) cubic feet, which agrees with the volume calculated using the first method.
What is volume?Volume is a measurement of the amount of space that an object occupies. It is the three-dimensional space occupied by an object. Volume is typically measured in cubic units such as cubic meters, cubic centimeters, cubic feet, and so on.
We can determine the volume of the rectangular prism in two different ways using the formula:
Volume = Length x Width x Height
First Method:
In the first method, we simply substitute the given dimensions of the rectangular prism into the formula and calculate the volume:
Volume = (3/4) ft x (3/8) ft x (3/4) ft
Volume = (9/32) ft³
Second Method:
In the second method, we can use the fact that the rectangular prism can be divided into 4 smaller rectangular prisms, each with dimensions (3/4) ft x (3/8) ft x (3/16) ft. We can calculate the volume of one of these smaller prisms and then multiply by 4 to get the total volume:
Volume of one smaller prism = (3/4) ft x (3/8) ft x (3/16) ft
Volume of one smaller prism = (27/256) ft³
Total volume = 4 x Volume of one smaller prism
Total volume = 4 x (27/256) ft³
Total volume = (27/64) ft³
To know more about rectangular prism visit:
https://brainly.com/question/29753475
#SPJ9
Find the numbers with the following property three times the sum of four and a number is less than seven times the same number
Answers
Let's represent the number with the variable "x". According to the given property, we can write the following equation:
3(x + 4) < 7x
Now, let's solve this inequality to find the range of numbers that satisfy the property.
3x + 12 < 7x
Subtract 3x from both sides:
12 < 4x
Divide both sides by 4 (since the coefficient of x is 4):
3 < x
So, the range of numbers that satisfy the given property is x > 3.
Therefore, any number greater than 3 will satisfy the condition. For example, 4, 5, 6, 7, 8, etc.Step-by-step explanation:
According to the problem, we know that:
3(4 + x) < 7x
Simplifying:
12 + 3x < 7x
Subtracting 3x from both sides:
12 < 4x
Dividing both sides by 4:
3 < x
So the number we're looking for must be greater than 3.
The population of a town increased from 3700 in 2005 to 5900 in 2009. Find the absolute and relative (percent) increase.
Absolute increase:
Relative increase:
%
Answers
The absolute increase in population is 2200, and the relative increase is approximately 59.46%.
To find the absolute and relative increase in population, we can use the following formulas:
Absolute increase = Final value - Initial value
Relative increase = (Absolute increase / Initial value) * 100%
Given the population in 2005 is 3700 and the population in 2009 is 5900, we can calculate the absolute and relative increase as follows:
Absolute increase = 5900 - 3700 = 2200
To calculate the relative increase, we need to divide the absolute increase by the initial value and then multiply by 100:
Relative increase = (2200 / 3700) * 100% ≈ 59.46%
Therefore, the absolute increase in population is 2200, and the relative increase is approximately 59.46%.
The absolute increase represents the actual difference in population count between the two years, while the relative increase gives us the percentage change relative to the initial value. In this case, the population increased by 2200 individuals, and the relative increase indicates that the population grew by approximately 59.46% over the given period.
Note that the relative increase is expressed as a percentage, which makes it easier to compare changes across different populations or time periods.
for more such question on population visit
https://brainly.com/question/30396931
#SPJ8
Which speed is the fastest?
A. 2/3 mile in 8 hours
B. 1/2 mile in 3 hours
C. 16 miles in 4 hours
D. 8 miles in 2/3 hours
Answers
Answer:
D
Step-by-step explanation:
A) 2/3 miles in 8 hours = 2 miles in 24 hours
B) 1/2 miles in 3 hours = 4 miles in 24 hours
C) 16 miles in 4 hours = 96 miles in 24 hours
D) 8 miles in 2/3 hours = 288 miles in 24 hours
Hence the answer is D (8 miles in 2/3 hours)
A coin and a die are tossed simultaneously.
a) What is the probability that the result is tails and an odd number?
b) What is the probability of getting tails or an odd number?
c) What are the probabilities of getting tails, or of getting an odd number, but not both simultaneously?
Answers
The probabilities are given as follows:
a) Tails and odd number: 1/4.
b) Tails or odd number: 3/4.
c) Tails or odd number, but not simultaneously: 1/2.
How to obtain the probabilities?The probability of an event in an experiment is calculated as the number of desired outcomes of the experiment divided by the number of total outcomes of the experiment.
For each event, the probabilities are given as follows:
Tails: 1/2.Odd number on the dice: 1/2.Hence the probability of both events is of:
p = 1/2 x 1/2 = 1/4.
The or probability is composed as follows:
Tails and odd: 1/4.Tails and even: 1/2 x 1/2 = 1/4.Heads and off: 1/2 x 1/2 = 1/4.Hence the ´probability is of:
3 x 1/4 = 3/4.
Removing the simultaneous event, the probability is of:
3/4 - 1/4 = 2/4 = 1/2.
More can be learned about probabilities at https://brainly.com/question/14398287
#SPJ1
6. Emily receives an inheritance of $20,000 and decides to invest the money. She puts some money in her savings
account that earns 1.5% simple interest per year. The remaining money is invested in a bond fund that returns 4.5% and a
stock fund that returns 6.2%. She makes a total of $942 at the end of 1 yr. If she invested twice as much in the bond fund
as the stock fund, determine the amount that she invested in each fund.
Answers
Emily funded $6000 in stocks and $12,000 in bond funds. She also funded the remaining $2,000 in her savings account.
Future value = $20,000
Simple interests rate = 1.5%
The return rate on bonds= 4.5%
The return rate on stocks = 6.2%
Total amount made on invests = $942
Time period = 1 year
Let us assume that the amount of money Emily invested = x
Amount invested in stock = y
If the amount is twice = 2y
The interest earned = x * 0.015
Interest on bond = 2y * 0.045
Interest on stocks = y * 0.062
The equation will be:
(x * 0.015) + (2y * 0.045) + (y * 0.062) = 942
0.015x + 0.152y = 942 ------ Equation 1
Total future value is given as $20,000
x + 2y + y = 20000
x + 3y = 20000
x = 20000 - 3y
Substituting the x value in the first equation:
0.015(20000 - 3y) + 0.152y = 942
300 - 0.045y + 0.152y = 942
0.107y = 642
y = 6000
Therefore, we can conclude that Emily funded $6000 in stocks and $12,000 in bond funds.
To learn more about the amount invested
https://brainly.com/question/31636719
#SPJ1
Fred is making a bouquet of carnations and roses. The carnations cost $5.25 in all. The roses cost $1.68 each. How many roses did Fred use if the bouquet cost $18.69 in all?
wrong answers reported
right answers get brainiest
Answers
Answer:
8 roses
Step-by-step explanation:
First start by subtracting $18.69 by $5.25 because you already know how much the carnations cost and how much the bouquet cost in all. When you subtract 18.69 by 5.25 you should get $13.44. If each rose cost $1.68 then divide 13.44 by 1.68 to get the amount of roses in the bouquet.
If this figure is dilated by a scale factor of 3, what would the new coordinates be?

Answers
Answer:
J (-3,3), G (0,3), H (4,9), I (3,3)
Step-by-step explanation:
When your dilating a figuring it either gets larger or smaller. Since this is a positive number, and it is not a fraction then the figure is getting larger. Now you multiply each of the original coordinates by 3 to get the dilated coordinates.
(For learning purposes only)
Solve for X
6y = 2x + 10
Answers
Answer: x=3y−5
Step-by-step explanation: 6y=2x+10
Swap sides so that all variable terms are on the left hand side.
2x+10=6y
Subtract 10 from both sides.
2x=6y−10
Divide both sides by 2.
2
2x
=
2
6y−10
Dividing by 2 undoes the multiplication by 2.
x=
2
6y−10
Divide 6y−10 by 2.
x=3y−5
The 9th graders are selling tickets to raise money for a class field trip. They are selling student tickets for $5 and adult tickets for $9. The 9th graders received a total of $240 from sales. In total, 40 tickets were sold. Write a system to represent this situation. Be sure to define your variables. Use your system to determine how many tickets of each type the students sold.
Answers
Answer:
Total number of adult tickets sold = 10
Total Number of Students tickets sold = 30
Step-by-step explanation:
Let \(x\) be the number of student tickets sold.
Let \(y\) be the number of adult tickets sold.
As per the question statement, total tickets sold are 40.
\(x +y =40 ...... (1)\)
Price of each student ticket = $5
Sales from students' tickets = Price of each students ticket \(\times\) Number of students tickets sold
Sales from student's tickets = 5 \(\times x\)
Price of each adult ticket = $9
Sales from adult's tickets = Price of each adult's ticket \(\times\) Number of adult tickets sold
Sales from student's tickets = 9 \(\times y\)
Total sales is done by students and adult tickets is $240 as per the question statement.
\(\Rightarrow 5x + 9y = 240 ......(2)\)
Solving equations (1) and (2) using elimination method:
Equation \((2) - 5 \times (1)\) :
\(5x + 9y -5x-5y = 240-200\\\Rightarrow 4y = 40\\\Rightarrow y =10\)
Total number of adult tickets sold = 10
Putting \(y=10\) in equation (1):
\(x+10 = 40\\\Rightarrow x = 30\)
Total number of students tickets sold = 30
Total number of adult tickets sold = 10
Total Number of Students tickets sold = 30
A roasted turkey is taken from an oven when its temperature has reached 185 Fahrenheit and is placed on a
table in a room where the temperature is 75 Fahrenheit. Give answers accurate to at least 2 decimal
places.
(a) If the temperature of the turkey is 153 Fahrenheit after half an hour, what is its temperature after 45
minutes?
Fahrenheit
(b) When will the turkey cool to 100 Fahrenheit?
hours.
Answers
After answering the presented question, we can conclude that As a equation result, the turkey's temperature after 45 minutes is roughly 134.43 Fahrenheit.
What is equation?In mathematics, an equation is a statement that states the equality of two expressions. An equation consists of two sides separated by an algebraic equation (=). The argument "\(2x + 3 = 9,\)" for example, states that the sentence "\(2x + 3\)" equals the value "9." The goal of solving equations is to find the value or values of the variable(s) that will allow the equation to be true. Equations can be simple or complex, linear or nonlinear, and contain one or more parts. In the equation "\(x2 + 2x - 3 = 0\)," the variable x is raised to the second power. Lines are used in many areas of mathematics, including algebra, calculus, and geometry.
a. \(dT/dt=-k(T-Ts)\)
\(-kdt=(DT/(T-Ts)\)\()\)
When both sides are combined, the following results:
\(-kt + C = ln|T - Ts|\)
where C is the integration constant. To calculate C, we can start with the assumption that the turkey is 185 degrees Fahrenheit when it comes out of the oven:
\(ln|185 - 75| = -k(0) + C\)
\(C = ln(110) (110)\)
As a result, the equation relating the temperature of the turkey to time is:
\(-kt+In|T-75|=-kt+In(110)\)
\(T=e(-ktIn(110)+75\)
\(T=110e(-0.5k)+75\)
\(T=110e(-0.75k+75 T134.43\) degrees Fahrenheit
As a result, the turkey's temperature after 45 minutes is roughly 134.43 Fahrenheit.
To know more about equation visit:
brainly.com/question/649785
#SPJ9
The are of a square is 36 square feet. Which of the following measures is closest to the length of the diagonal?A).6.0ftB).6.2ftC).8.3ftD).8.5ft
Answers
then with the Pythagorean theorem we find the diagonal
\(\begin{gathered} c^2=a^2+b^2 \\ c^2=6^2+6^2 \\ c^2=36+36 \\ c^2=72 \\ c=\sqrt[]{72} \\ c=8.485 \end{gathered}\)answer: the length of the diagonal is 8.5 ft
Alexander is a stockbroker. He eams 11% commission each week Last week, he
sold $7,100 worth of stocks. How much did he make last week in commission? The averages that
same amount each week, how much did he make in commission in 2011
Answers
(A): 825
(B): 42,900
Evaluate the expression when y=30 and z=6 .y + z^2/y - 4z
Answers
The answer is 11.
what is the volume of the cylinder below height 15 radius 11
Answers
Answer:
πr^2 h
π(11)^2 (15)
= 1815π or = 5701
A group of friends were working on a student film that had a budget of $800. They spent all their budget on equipment and props. They used 73% of their budget on props. How much money did they spend on equipment?
Answers
Answer:
216
Step-by-step explanation:
800 ÷ 100 = 8
8 = 1%
73 x 8 = 584
800 - 584 = $216
The 7th grade has 220 students. Three-fifths of the students are girls. How many boys are in the 7th grade?

Answers
Answer:
88 are boys
Step-by-step explanation:
220 times 3/5 = 132
220-132 =88
The number of boys in the 7th grade is B = 88 boys
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as B
Now , the value of B is = number of boys
Substituting the values in the equation , we get
If three-fifths of the students are girls, then two-fifths must be boys, since the total fraction of students is equal to 1
On simplifying the equation , we get
To find the number of boys in the 7th grade, we can start by calculating the fraction of boys:
( 2/5 ) x 220 = 88
Hence , there are 88 boys in the 7th grade.
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ2
..................................

Answers
Answer:
26√5 + 2√10
hope it helps and your day will be full of happiness
Answer:
d) 26√5 + 2√10
Step-by-step explanation:
Given equation,
→ 2√5(13 + √2)
Simplifying the given expression,
→ 2√5(13 + √2)
→ 26√5 + 2√10
Hence, option (d) is the answer.
Consider the following question.
"Do you watch television every day?"
Which of the following statements BEST explains why the question is NOT a statistical question?
A The question does not anticipate variability in the answers
B The question results in a single absolute answer.
C The question may be answered differently by different people.
D. The question does not require an explanation
Answers
Answer:
a
Step-by-step explanation:
Answer:
C, the only info for the question is about yourself which is a survery question
Step-by-step explanation:
according to a recent pew research center report, many american adults have made money by selling something online. in a random sample of 4579 american adults, 914 reported that they earned money by selling something online in the previous year. assume the conditions for inference are met. construct a 98% confidence interval for the proportion of all american adults who would report having earned money by selling something online in the previous year. (0.1859, 0.2133) (0.1899, 0.2093) (0.1994, 0.1998) (0.1880, 0.2112) (0.1937, 0.2037)
Answers
98% confidence interval for the proportion of all american adults who would report having earned money by selling something online in the previous year by using z-score. The correct answer is (0.1859, 0.2133)
The point estimate for the proportion of American adults who earned money by selling something online in the previous year is:
p-hat = 914/4579 = 0.1995
To construct a 98% confidence interval for the population proportion, we can use the formula:
p-hat ± z*(sqrt(p-hat*(1-p-hat)/n))
where z is the z-score associated with the desired confidence level (98% corresponds to a z-score of 2.33), and n is the sample size. Plugging in the values, we get:
0.1995 ± 2.33*(sqrt(0.1995*(1-0.1995)/4579))
Simplifying this expression, we get:
(0.1859, 0.2133)
Therefore, the correct answer is (0.1859, 0.2133). This means we are 98% confident that the true proportion of American adults who earned money by selling something online in the previous year lies between 0.1859 and 0.2133.
To know more about z-score:
https://brainly.com/question/15016913
#SPJ4
-
A rectangle has dimensions 2x – 12 by 3x + 9 and area 60 cm². What are the actual
dimensions of the rectangle?
Answers
Answer:
2 x 30 cm
Step-by-step explanation:
L x W = 60
(2x-12)(3x+9) = 60
6x^2 -18x-168=0
use quadratic fromula to find x = 7 or -4 (throw out)
the sides then become ( using 7)
2 and 30 cm
y’all plz help fast
