Find the probability that a randomly
selected point within the square falls in the
red-shaded triangle.
Enter as a decimal rounded to the nearest hundredth.
Enter

Answers
Answer:
0.13
Step-by-step explanation:
You want the probability that a point in the figure lies in the red shaded area.
ProbabilityThe desired probability is the ratio of the red area to the entire area.
Red areaThe red area is half a 4×4 square, so is (4×4)/2 = 8 square units.
Total areaThe area of the whole figure is that of an 8×8 square, so is (8×8) = 64 square units.
RatioThe ratio of the areas is ...
red/whole = 8/64 = 1/8 = 0.125 ≈ 0.13
The probability that a randomly selected point falls in the red area is about 0.13.
<95141404393>
Related Questions
Sam plans to buy $32.50 in Beads and $9.50 in string but he has a coupon of 20% how much did he spend
Answers
Answer:
$33.60
Step-by-step explanation:
$32.50 + $9.50 = $42.00
20% is changed to .20
Multiply 42.00 x .20 = $8.40 percentage discount
$42.00 - $8.40 = $33.60 is how much he spent
Two of the angles in a triangle measure 1 degree and 5 degrees.what is the measure of the third angle?
Answers
Answer:
174
Step-by-step explanation:
All 3 angles in a triangle add up to 180.
So we are given 2 angles and we need to find angle 3. I am going to call the missing 3rd angle 'x'.
1 + 5 + x = 180.
Solve for x
6 + x = 180
Subtract 6 from both sides
x = 174
PLEASEEEE I BEG YOU PLZZZ SOMEBODY GIVE ME THE RIGHT ANWSERSS TO THESEEE AND I DONT WNAT ANY WRONG ONES ARE REPORT JUST HELPP CUSE LAST WEEK EVERYBODY GOT IT WRONG!!!!!



Answers
Answer:
Step-by-step explanation:
Question 1: C
1 multiplied by 5 = 5
1 plus 5 = 6
So you get: (x+5)(x+1) which means x = -5 or -1
Question 2: B
2 multiplied by -4 = - 8
2 plus -4 = -2
So you get: (x-4)(x+2) which means x = 4 or -2
Write the equation of the line in slope-intercept form that passes through
the point (-3, 5) and is parallel to y = -2/3 x
Answers
Answer:
y= -2/3x+3
Step-by-step explanation:
Parallel lines have the same slope but different y-intercepts.
y=-2/3x is your original equation
Your slope is still -2/3
y=mx+b
y=-2/3x + b
Substitute the points from the coordinates
5 = -2/3(-3) + b
5 = 2 + b
-2 -2
b=3
Your parallel line equation is: y= -2/3x+3
Have a great day!
15 NEED HELP ASAP WILL GIVE BRAINLY

Answers
Answer:
The first answer is correct because the angle it gives you in the 3rd picture at the bottom left is congruent with X, therefore makeing the X 100.
Step-by-step explanation:
assume that a simple random sample has been selected from a normally distributed population. state the final conclusion. round the test statistic to two decimal places. test the claim that the mean lifetime of a particular car engine is greater than 220,000 miles. sample data are summarized as , miles, and miles. use a significance level of . the hypotheses are and .
Answers
There is evidence to support the claim that the mean lifetime of a particular car engine is greater than 220,000 miles.
Based on the information given, we can use a one-sample t-test to test the claim that the mean lifetime of a particular car engine is greater than 220,000 miles.
The null hypothesis is that the true mean of the population is equal to or less than 220,000 miles, and the alternative hypothesis is that the true mean is greater than 220,000 miles.
Let's assume that the sample size is large enough for the Central Limit Theorem to apply. We can use a t-test with the following formula:
t = (X- μ) / (s / √n)
Where:
X = sample mean
μ = hypothesized population mean
s = sample standard deviation
n = sample size
From the sample data provided, we have:
X= 225,000 miles
s = 4,000 miles
n = 25
Using a significance level of α = 0.05, the critical value for a one-tailed t-test with 24 degrees of freedom is 1.711.
Plugging in the numbers, we get:
t = (225,000 - 220,000) / (4,000 / √25) = 2.50
Since the calculated t-value (2.50) is greater than the critical value (1.711), we reject the null hypothesis. This means we have sufficient evidence to conclude that the mean lifetime of a particular car engine is greater than 220,000 miles at the α = 0.05 level of significance.
Therefore, we can conclude that there is evidence to support the claim that the mean lifetime of a particular car engine is greater than 220,000 miles.
To learn more about standard deviation visit:https://brainly.com/question/23907081
#SPJ11
the expression x^3/2 x square root of x can be expressed in the form of x^a , where the value of a is
Answers
The expression can be expressed in the form of x².
The value of a is 2.
What is an expression?One mathematical expression makes up a term. It might be a single variable (a letter), a single number (positive or negative), or a number of variables multiplied but never added or subtracted. Variables in certain words have a number in front of them. A coefficient is a number used before a phrase.
Given:
We have an expression,
\(x^{3/2}\)×√x.
Simplifying,
\(x^{3/2}\)×√x,
= \(x^{3/2} x^{1/2}\)
= \(x^{3/2+1/2}\)
= \(x^{2}\)
Therefore, the value of a is 2.
To learn more about the expression;
brainly.com/question/24242989
#SPJ1
Evaluate each expression to four decimal places.
e³/₂
Answers
The value of e³/₂ is 4.4758
e in here is considered as Euler's number. Euler's number is a numerical constant which is often used in mathematical calculations. the value of e can be taken into consideration as 2.71828.
The given expression e⁽³÷²⁾ can also be written as √e³. First the cube of e is calculated which is then followed by finding the square root of the calculated value.e⁽³÷²⁾ = √e³. The value of e³ when calculated is 2.7182 x 2.7182 x 2.7182 = 20.0855
Now taking the square root of the calculated value is √20.0855 is 4.4816
Therefore the value of e⁽³÷²⁾ up to four decimal places is 4.4816
Learn more about evaluation up to four decimal places here
https://brainly.com/question/17255119
#SPJ4
Why do we square the residuals when using the least-squares line method to find the line of best fit?
Answers
We square the residuals when using the least-squares line method to find the line of best fit because we believe that huge negative residuals (i.e., points well below the line) are just as harmful as large positive residuals (i.e., points that are high above the line).
What do you mean by Residuals?We treat both positive and negative disparities equally by squaring the residual values. We cannot discover a single straight line that concurrently minimizes all residuals. The average (squared) residual value is instead minimized.
We might also take the absolute values of the residuals rather than squaring them. Positive disparities are viewed as just as harmful as negative ones under both strategies.
To know more about the Least-Squares Line method, visit:
https://brainly.com/question/14940432
#SPJ4
Write the trigonometric expression as an algebraic expression in u. cot (sin 1u) cot (sin 1] (Type an exact answer, using radicals as needed.)
Answers
We can simplify the expression by combining terms and simplifying further based on any specific values of u or 1.
To express the trigonometric expression cot(sin(1u)) cot(sin(1]) as an algebraic expression in u, we need to apply trigonometric identities and simplify it.
Let's start by using the identity cot(x) = 1/tan(x):
cot(sin(1u)) cot(sin(1]) = (1/tan(sin(1u))) (1/tan(sin(1]))
Next, we'll use the identity tan(x) = sin(x)/cos(x) to rewrite the tangents in terms of sine and cosine:
= (1/(sin(1u)/cos(1u))) (1/(sin(1)/cos(1]))
Simplifying further, we can multiply the reciprocals:
= (cos(1u)/sin(1u)) (cos(1)/sin(1))
Now, let's use the identity sin(2x) = 2sin(x)cos(x) to express the sines and cosines in terms of sine of half-angles:
= (cos(1u)/(2sin(1/2u)cos(1/2u))) (cos(1)/(2sin(1/2)cos(1/2)))
= (cos(1u)/2sin(1/2u)cos(1/2u)) (cos(1)/2sin(1/2)cos(1/2))
Since cos(x)cos(y) = (1/2)[cos(x+y)+cos(x-y)], we can use this identity to simplify the expression further:
= (cos(1u)/2sin(1/2u)(1/2)[cos(1/2+1/2u)+cos(1/2-1/2u)]) (cos(1)/2sin(1/2)cos(1/2))
= (cos(1u)/4sin(1/2u)[cos(1/2+1/2u)+cos(1/2-1/2u)]) (cos(1)/2sin(1/2)cos(1/2))
Now, we can simplify the expression by combining terms and simplifying further based on any specific values of u or 1.
Learn more about trigonometric here:
https://brainly.com/question/29156330
#SPJ11
please answer this question for me
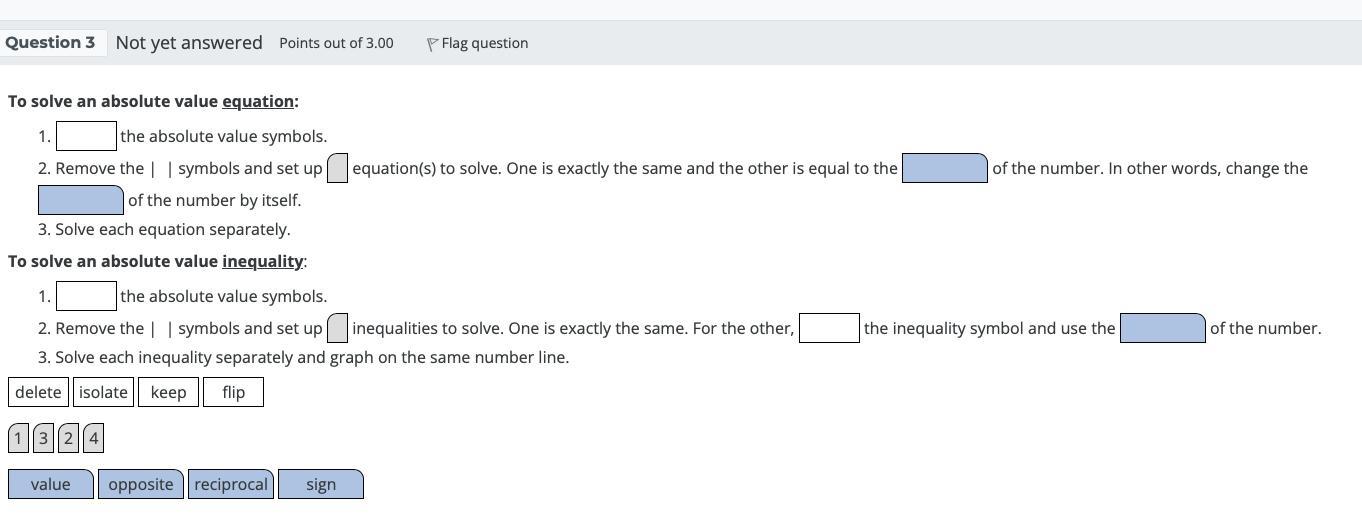
Answers
1) isolate
2a) opposite
2b) sign
1) delete
2a) flip
2b) reciprocal
isolate
opposite
sign
Delete
flip
Reciprocal
please help asap/ Choose the sentence that best uses a synonym as a context clue to clarify the meaning of the italicized word.

Answers
Answer:
D.
Step-by-step explanation:
The answer is D. because the vicinity of the playing field can be associated with the bleachers.
D.
Explanation:
a) Calculate the size of angle x in the diagram
below.
b) Work out the bearing of A from B.

Answers
The angle x in the diagram is 98 degrees.
How to find the angles in parallel lines?When parallel lines are cut by a transversal line, angle relationships are formed such as corresponding angles, alternate interior angle, alternate exterior angles, vertically opposite angles, same side interior angles etc.
Therefore, let's find the angle of x using the angle relationships as follows:
The size of the angle x can be found as follows:
82 + x = 180(same side interior angles)
Same side interior angles are supplementary.
Hence,
82 + x = 180
x = 180 - 82
x = 98 degrees
learn more on angles here: brainly.com/question/24195209
#SPJ1
Find the area of the figure below
77.25 cm^2 154.5 cm^2 87.55 cm^2 175.1 cm^2

Answers
The area of the given triangle is 87.55 square centimeter.
From the given triangle, base=17 cm and height=10.3 cm.
The basic formula for the area of a triangle is equal to half the product of its base and height, i.e., A = 1/2 × b × h.
Here, area of a triangle = 1/2 ×17×10.3
= 87.55 square centimeter
Therefore, area of the given triangle is 87.55 square centimeter.
To learn more about the area of a triangle visit:
brainly.com/question/27701864.
#SPJ1
I really really need the answer to this NOW

Answers
Answer:
185 and 1/3
Step by step explanation
What is the sign of c÷d when c >0 and d < 0.
Plzzz helppp im in class right now
Answers
Answer:
Negative
Step-by-step explanation:
Assume that you mean if c÷d is positive or negative when c > 0 and d < 0
c > 0 means that c is positive
d < 0 means that d is negative
positive divides negative is always negative.
Thus, c÷d is negative when c > 0 and d < 0
.Independent random samples of business managers and college economics faculty were asked to respond on a scale from 1 (strongly disagree) to 7 (strongly agree) to this statement: Grades in advanced economics are good indicators of students’ analytical skills. For a sample of 70 business managers, the mean response was 4.4 and the sample standard deviation was 1.3. For a sample of 106 economics faculty, the mean response was 5.3 and the sample standard deviation was 1.4.
a) Test, at the 5% level, the null hypothesis that the population mean response for business managers would be at most 4.0. (10marks)
b) Test, at the 5% level, the null hypothesis that the population means are equal against the alternative that the population mean response is higher for economics faculty than for business managers. Assume unequal variance.
Answers
Step-by-step explanation:
a) The test statistic is (4.4-4)/(1.3/sqrt(70)) = 2.83. The p-value is 0.0023. Since the p-value is less than 0.05, we reject the null hypothesis.
b) The test statistic is (5.3-4.4)/sqrt((1.4^2/106)+(1.3^2/70)) = 4.09. The p-value is less than 0.0001. Since the p-value is less than 0.05, we reject the null hypothesis.
Help out please need this now

Answers
Answer:
0.2266739274
Step-by-step explanation:
[√(150 + 214.9) ] / (9.85 - 0.4)²
a gambler is betting on a coin-flip game. if it is head he wins $1 but if it is tail he loses $1. suppose the coin is fair, that is, the probability of head or tail is 1/2, what is the standard deviation of his payoff?
Answers
The gambler's payoff has a standard deviation of $1. The gambler can expect to win or lose $1 on average for each coin flip, and there is a high degree of variability in the possible outcomes of the game.
The standard deviation of the gambler's payoff can be calculated using the following formula:
σ = √(Σ(xi - μ)^2 * P(xi))
where σ is the standard deviation, xi is the possible outcome of the game, μ is the expected value of the game, and P(xi) is the probability of each outcome.
In this case, there are two possible outcomes: winning $1 with probability 1/2 and losing $1 with probability 1/2. The expected value of the game is:
μ = (1/2 * $1) + (1/2 * -$1) = $0
To calculate the standard deviation, we need to determine the variance first. The variance can be calculated as:
σ^2 = Σ(xi - μ)^2 * P(xi)
= (1 - 0)^2 * 1/2 + (-1 - 0)^2 * 1/2
= 1
Therefore, the standard deviation is:
σ = √1 = 1
To learn more about click standard deviation on,
https://brainly.com/question/13720915
#SPJ4
Mr brown and his two kids go to London by train. What's 60 percent of £12?
Answers
Answer:
7.2£
Step-by-step explanation:
I used pencil and paper for this so I am sure
Hope this helps!!! If so please give brainliest!!!
look at each expression. is it equivalent to "the quotient of 10 plus x and y minus 3"?

Answers
Answer:
B
Step-by-step explanation:
B
The numerator is 10 + x.
The denominator is y - 3.
What is the product (6√5 - 6i) (√3 + √3i) in polar form example : (e - fi) and what quadrant of the complex plane does the product lie?
Answers
Answer: Plain: the product is 24 ∠ 15° in polar form. This means that the magnitude of the product is 24 and the angle between the positive real axis and the line connecting the origin and the product is 15°, measured counterclockwise.
Step-by-step explanation: To multiply complex numbers in polar form, we multiply their magnitudes and add their angles. We can start by converting the given complex numbers from rectangular form to polar form:
6√5 - 6i = 6(√5 - i) = 12 ∠ -30°
(√3 + √3i) = √3(1 + i) = 2 ∠ 45°
where we have used the fact that ∠θ is the angle between the positive real axis and the line connecting the origin and the complex number a + bi, measured counterclockwise.
Now, we can multiply the two complex numbers in polar form:
(6√5 - 6i)(√3 + √3i) = 12 ∠ -30° * 2 ∠ 45°
= 24 ∠ 15°
Therefore, the product is 24 ∠ 15° in polar form. This means that the magnitude of the product is 24 and the angle between the positive real axis and the line connecting the origin and the product is 15°, measured counterclockwise.
To determine the quadrant of the complex plane in which the product lies, we note that the angle 15° is in the first quadrant (between 0° and 90°). Therefore, the product lies in the first quadrant of the complex plane.
O is the centre of the circle below
calculate the size of angle t
state any circle theorems that you used.

Answers
In the circle, angle t is solved to be
48 degreesHow to find angle tThe unknown angle labelled t is solved with the knowledge of the circle theorem which states that the angle subtended by an arc at the center is twice the angle subtended at the circumference.
Using this knowledge we have that
t = 2 * 24
t = 48 degrees
learn more about circle theorem at:
https://brainly.com/question/24261456
#SPJ1
A 25.0g metal sample required 130.0 calories to raise its temperature from 52.5\deg C to 72.5\deg C.
Answers
The specific heat capacity of the metal sample is 0.416 cal/g·°C. This value represents the amount of heat energy required to raise the temperature of one gram of the metal by one degree Celsius.
To determine the specific heat capacity of the metal sample, we can use the equation:
q = m * c * ΔT
Where:
q is the heat energy absorbed by the metal sample,
m is the mass of the metal sample,
c is the specific heat capacity of the metal, and
ΔT is the change in temperature.
Given:
m = 25.0 g (mass of the metal sample)
ΔT = (72.5°C - 52.5°C) = 20.0°C (change in temperature)
q = 130.0 cal (heat energy absorbed by the metal sample)
Rearranging the equation, we can solve for c:
c = q / (m * ΔT)
= 130.0 cal / (25.0 g * 20.0°C)
≈ 0.416 cal/g·°C
The specific heat capacity of the metal sample is approximately 0.416 cal/g·°C. This value represents the amount of heat energy required to raise the temperature of one gram of the metal by one degree Celsius.
To know more about capacity follow the link:
https://brainly.com/question/912113
#SPJ11
Which of the following is not a fundamental identity? A. cot θ = cos θ/sinθ. B. sec θ = 1/cosθ. C. sec^2 + 1 = tan^2θ. D. 1 + cot^2θ = csc^2θ.
Answers
A fundamental identity is an equation that relates the values of the trigonometric functions for a given angle. The equation cot θ = cos θ/sinθ is an example of a fundamental identity.
This identity states that the cotangent of an angle is equal to the cosine of the angle divided by the sine of the angle. The equation sec θ = 1/cosθ is another example of a fundamental identity. This identity states that the secant of an angle is equal to the reciprocal of the cosine of the angle. The equation sec^2 + 1 = tan^2θ is also a fundamental identity. This identity states that the square of the secant of an angle plus one is equal to the square of the tangent of the angle. The equation 1 + cot^2θ = csc^2θ is not a fundamental identity. This equation states that one plus the square of the cotangent of an angle is equal to the square of the cosecant of the angle. This equation is not a fundamental identity because it does not relate the values of the trigonometric functions for a given angle.
Learn more about trigonometric functions here:
https://brainly.com/question/6904750
#SPJ4
When we describe relationships between variables, a correlation nearer to 1.00 (plus or minus) indicates that?
Answers
When we describe relationships between variables, a correlation nearer to 1.00 (plus or minus) indicates the relationship between variables is strong.
The strength and direction of a relationship between two or more variables are described by the statistical measure of correlation, which is given as a number. However, a correlation between two variables does not necessarily imply that a change in one variable is the reason for a change in the values of the other.
When correlation is known, predictions can be made using it. Knowing a score on one measure helps us predict another that is closely related to it more accurately. The forecast will be more accurate the stronger the correlation between/among the variables.
Learn more about correlation here
https://brainly.com/question/4219149
#SPJ4
Simplify
-5|( 3 – 5•3^2)+2^3|•|4-2^3
Answers
Answer:
-232
Step-by-step explanation:
-5|+23|·|4-23|=-5|8|·|4-23|
-5|8|·|4-23|=-5|8|·|-4|
-5|8|·|-4|=-58·|-4|
-58·|-4|=-58·4
-58·4=-232
a quality control inspector has drawn a sample of 17 light bulbs from a recent production lot. suppose 30% of the bulbs in the lot are defective. what is the probability that between 3 and 6 (both inclusive) bulbs from the sample are defective? round your answer to four decimal places.
Answers
Answer: This is a binomial distribution problem with parameters n = 17 and p = 0.3, where n is the sample size and p is the probability of a defective bulb. We need to find the probability that between 3 and 6 (both inclusive) bulbs from the sample are defective.
Let X be the number of defective bulbs in the sample. Then X has a binomial distribution with parameters n = 17 and p = 0.3, i.e., X ~ B(17, 0.3).
We want to find P(3 ≤ X ≤ 6). Using the binomial probability formula, we have:
P(3 ≤ X ≤ 6) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)
= (17 choose 3)(0.3^3)(0.7^14) + (17 choose 4)(0.3^4)(0.7^13) + (17 choose 5)(0.3^5)(0.7^12) + (17 choose 6)(0.3^6)(0.7^11)
≈ 0.1566 (rounded to four decimal places)
Therefore, the probability that between 3 and 6 (both inclusive) bulbs from the sample are defective is approximately 0.1566.
Step-by-step explanation:
what is the value of 3.5(11)+1.9(11)+1.6(11)
Answers
Answer:
77
Step-by-step explanation:
3.5 ( 11 ) = 38.5
1.9 ( 11 ) = 20.9
1.6 ( 11 ) = 17.6
38.5 + 20.9 + 17.6
= 77
hope this helps
The measure of an angle is 100.3°. What is the measure of its supplementary angle?
Answers
Answer:
79.7°
Step-by-step explanation:
You hava to do this =
\(180-100.3=79.7\)
Answer:
79.7°
Step-by-step explanation:
Supplementary angles add up to 180°
100.3 + x = 180
Subtract 100.3 from both sides
x = 79.7°