Find the probability that a randomly
selected point within the circle falls
in the red shaded area (square).
r = 4 cm
4 √2 cm
[? ]%
round to the nearest tenth of a percent.
Answers
The probability that a randomly selected point within the circle falls in the red shaded area is approximately 49.3%.
To find the probability that a randomly selected point within the circle falls in the red shaded area, we need to find the ratio of the area of the red shaded region to the total area of the circle.
The area of the circle is π\(r^{2}\) = π\((4cm)^{2}\) = 16π \(cm^{2}\).
The diagonal of the square is equal to the diameter of the circle, which is 8cm. Therefore, the length of each side of the square is 4√2 cm.
The area of the square is (4√2 \(cm)^{2}\) = 32 \(cm^{2}\).
The area of the red shaded region is the difference between the area of the circle and the area of the square, which is 16π - 32 \(cm^{2}\).
So, the probability that a randomly selected point falls in the red shaded area is:
[(16π - 32)/16π] × 100% ≈ 49.3%
Therefore, the probability that a randomly selected point within the circle falls in the red shaded area is approximately 49.3%.
To know more about probability, refer here:
https://brainly.com/question/11234923#
#SPJ11
Related Questions
Solve the system of equations algebraically. Verify your answer using the graph.
y = 4x – 5
y = –3
What is the solution to the system of equations?
((StartFraction one-fourth EndFraction, negative 3), –3)
((StartFraction one-half EndFraction, negative 3), –3)
(–3, (negative 3, StartFraction 2 over 3 EndFraction))Solve the system of equations algebraically. Verify your answer using the graph.
y = 4x – 5
y = –3
What is the solution to the system of equations?
((StartFraction one-fourth EndFraction, negative 3), –3)
((StartFraction one-half EndFraction, negative 3), –3)
(–3, (negative 3, StartFraction 2 over 3 EndFraction))
Answers
Answer:
Step-by-step explanation:
To solve the system of equations algebraically, we need to substitute the second equation into the first equation and solve for x:
y = 4x – 5 (equation 1)
y = -3 (equation 2)
Substitute equation 2 into equation 1:
-3 = 4x – 5
Add 5 to both sides:
2 = 4x
Divide both sides by 4:
x = 1/2
Now, we can substitute this value of x back into either equation to find y:
y = 4(1/2) – 5 = -3
Therefore, the solution to the system of equations is (1/2, -3).
To verify this solution using the graph, we can plot the two equations on the same set of axes:
y = 4x – 5 (red line)
y = -3 (blue line)
The two lines intersect at the point (1/2, -3), confirming our solution.
Therefore, the answer is (B) (1/2, -3).
Drag each length to match it to an equivalent length. 2 yards 5 inches returned to choices list. 2 feet 8 inches4 yards9 feet2 yards 5 inches Length Equivalent Length 32 inches 77 inches 144 inches 3 yards
Answers
Answer:
2 yards 5 inches will be equivalent to 77 inches
Step-by-step explanation:
Given length -
2 yards 5 inches
One yard has 36 inches
Two yards will have 2*36 = 72 inches
Thus, 2 yards 5 inches will sum up to 72 inches + 5 inches = 77 inches
Hence, 2 yards 5 inches will be equivalent to 77 inches
Answer:
3 yards = 9 feet
77 inches = 2 yards 5 inches
48 inches = 1 yard 1 foot
32 inches = 2 feet 8 inches
I hope this helped!! <3
Solve for all positive roots of the equation below using SECANT METHOD. x^3-15x^2+62x-48. Round your answers to the nearest whole number.
Need it fast and correct
Answers
Using the secant method, the positive root of the equation x³ - 15x² + 62x - 48 is approximately 1.
To find the positive roots of the equation x³ - 15x² + 62x - 48 using the secant method, we need to start with two initial guesses, x₀ and x₁, such that f(x₀) and f(x₁) have opposite signs.
Let's begin the iterations:
1. Choose an initial guess, x₀ = 0, and calculate f(x₀):
f(x₀) = (0)³ - 15(0)² + 62(0) - 48 = -48
2. Choose a second initial guess, x₁ = 1, and calculate f(x₁):
f(x₁) = (1)³ - 15(1)² + 62(1) - 48 = 0
3. Calculate the next approximation, x₂, using the formula:
x₂ = x₁ - f(x₁) * ((x₁ - x₀) / (f(x₁) - f(x₀)))
Substituting the values:
x₂ = 1 - 0 * ((1 - 0) / (0 - (-48)))
x₂ = 1
4. Update the values of x₀ and x₁:
x₀ = x₁
x₁ = x₂
5. Repeat steps 2-4 until convergence is achieved.
- Calculate f(x₁):
f(x₁) = (1)³ - 15(1)² + 62(1) - 48 = 0
Since f(x₁) = 0, we have found a root.
6. Round the root to the nearest whole number:
x₁ ≈ 1
Therefore, the positive root of the equation x³ - 15x² + 62x - 48 is approximately 1.
To know more about secant method refer to the link:
https://brainly.com/question/32721765#
#SPJ11
QUESTION 1 · 1 POINT dy dy dx dy du du da Given y = f(u) and u = g(x), find by using Leibniz's notation for the chain rule: dx y=5u4 +4 u= -3.22 Provide your answer below: =
Answers
Using Leibniz's notation for the chain rule \(\frac{dy}{dx}\)= 540x⁸.
To find \(\frac{dy}{dx}\) using Leibniz's notation for the chain rule, we have:
y=f(u)=5u⁴+2
u=g(x)=3x³u
Let's start by finding \(\frac{dy}{du}\) and \(\frac{du}{dx}\) individually:
1. \(\frac{dy}{du}\):
To find \(\frac{dy}{du}\), we differentiate y with respect to u while treating uas the independent variable:
\(\frac{du}{dy}\) =d/du(5u⁴+2) = 20u³
2. \(\frac{du}{dx}\) :
To find \(\frac{du}{dx}\) , we differentiate u with respect to x:
\(\frac{du}{dx}\) = d/dx(3x³)=9x²
Now, we can apply the chain rule by multiplying \(\frac{dy}{du}\) and \(\frac{du}{dx}\) to find \(\frac{dy}{dx}\)
\(\frac{dy}{dx}\) = \(\frac{dy}{du}\) * \(\frac{du}{dx}\) = (20 u³)* (9x²)
Substituting u=3x³:
\(\frac{dy}{dx}\) = (20(3x³)³)⋅(9x²)
Simplifying:
\(\frac{dy}{dx}\) = 540 x⁸
Therefore, \(\frac{dy}{dx}\)=540x⁸ using Leibniz's notation for the chain rule.
The question should be:
QUESTION 1 · 1 POINT Given y = f(u) and u = g(x), find dy/dx by using Leibniz's notation for the chain rule:
dy/dx = (dy/du)* (du/dx) , y=5u⁴ + 2 , u= 3x³
To learn more about chain rule: https://brainly.com/question/29498741
#SPJ11
PLEASE HELP ME
A deli is trying out new labels for their cylindrical-shaped wheels of cheese. The label covers the entire wheel except the circular top and bottom.
If the wheel has a radius of 22 centimeters and a height of 16 centimeters, how many square centimeters of the wheel does the label cover? (Approximate using pi equals 22 over 7)
15,488 over 7 square centimeters
36,784 over 7 square centimeters
1,936 over 7 square centimeters
340,736 over 7 square centimeters
Answers
The label covers 11,936 over 7 square centimeters of the wheel.
The cylindrical-shaped wheel of cheese has a radius of 22 centimeters and a height of 16 centimeters. The label covers the entire wheel except the circular top and bottom. Therefore, the area covered by the label is the lateral surface area of the cylinder.
The lateral surface area of a cylinder can be calculated using the formula 2πrh, where r is the radius of the base, h is the height, and π is approximately equal to 22/7.
Substituting the given values, we get:
Lateral surface area = 2 × (22/7) × 22 × 16
Lateral surface area = (44/7) × 22 × 16
Lateral surface area = 1,936 square centimeters (approx.)
Therefore, the label covers approximately 1,936/7 square centimeters of the wheel. The closest option is (C) 1,936 over 7 square centimeters.
To learn more about centimeters here:
https://brainly.com/question/19098836
#SPJ1
if 4y= 2.6,find the value of 20y + 3
Answers
Answer:
16
Step-by-step explanation:
4y = 2.6
y = 0.65
20y + 3
= 20 × 0.65 + 3
= 13 + 3
= 16
#CMIIW
A seasoning blend is 4\%4%4, percent onion powder, by mass. How much pure onion powder should they include in a 72\,\text{g}72g72, start text, g, end text bottle to make the final blend have 20\ , percent onion powder? khan academy
Answers
They need to put 14.4 grams of onion powder in each bottle.
Given,
The quantity of onion powder in a seasoning blend = 4%
We have to find the quantity of pure onion powder should they include in a 72g bottle to make the final blend have 20% onion powder;
How much is a percentage?
A percentage is a certain number or part in every hundred. It is a fraction with the denominator 100, and the symbol for it is "%."
Here,
Let x be the seasoning blend.
Now, 4% of 72=20% of x
⇒ 0.04×72=0.2×x
⇒ 0.2x=2.88
⇒ x=2.88/0.2
⇒ x=14.4 g
Therefore, a container should contain 14.4 grams of onion powder.
Learn more about quantity of onion powder here;
https://brainly.com/question/29332582
#SPJ4
For each ordered pair, determine whether it is a solution to the system of equations. -4x+5y=6 7x-3y=1 \table[[(x,y),Is it a solution? ],[,Yes ],[No,],[(0,-8),0],[0,(-2,-5)],[0,0],[(-9,-6),0],[0,(2,1)],[0,0]]
Answers
The ordered pairs that is a solution to the system is (1, 2)
(x,y), Is it a solution
(0,-8) No
(-2,-5) No
(-9,-6) No
(2, 1) No
How to determine whether the ordered pairs are solutions to the systemFrom the question, we have the following parameters that can be used in our computation:
-4x + 5y = 6
7x - 3y = 1
Make the coefficients of x in the equations equivalent
So, we have
-28x + 35y = 42
28x - 12y = 4
Add the equations
23y = 46
So, we have
y = 2
Next, we have
-4x + 5y = 6
-4x + 5(2) = 6
-4x + 10 = 6
-4x = -4
x = 1
So, the solution is (1, 2)
Read more about system of equations at
https://brainly.com/question/32492977
#SPJ4
Question
For each ordered pair, determine whether it is a solution to the system of equations.
-4x + 5y = 6
7x - 3y = 1
(x,y), Is it a solution? [,Yes ],[No,]
(0,-8) ___ ____
(-2,-5) ___ ____
(-9,-6) ___ ____
(2,1) ___ ____
Solve.
Sy= 2x - 6
4x – 2y = 14
Use the substitution method
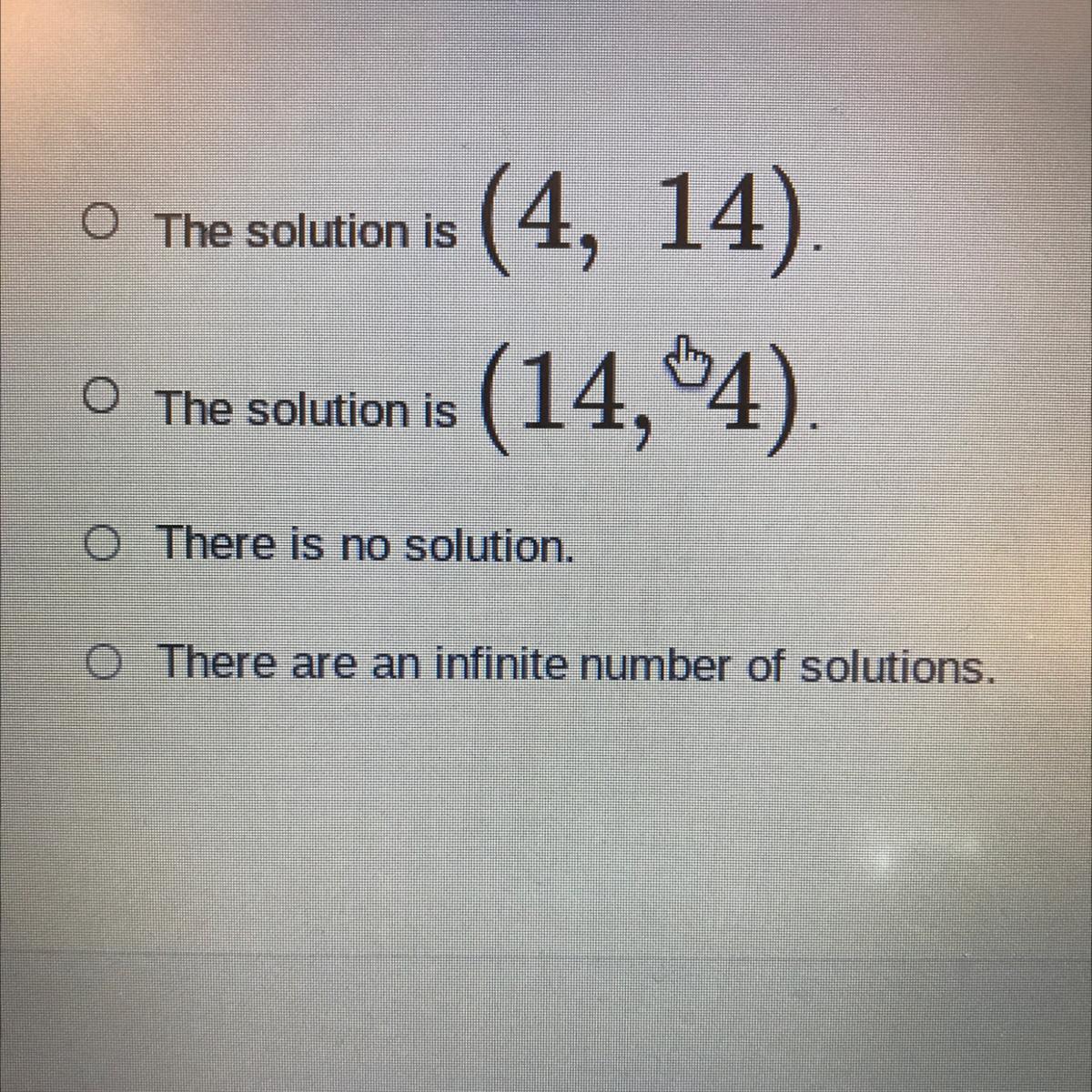
Answers
Answer:
14.4 i hope it helped you
What is the midpoint of a segment in the complex plane with endpoints at 6 â€"" 2i and â€""4 6i? 1 2i 2 i 2 4i 5 4i
Answers
The midpoint of a segment in the complex plane with endpoints at 6 - 2i and -4 + 6i is 1 + 2i.
To find the midpoint of a segment in the complex plane, we average the coordinates of the endpoints. The first endpoint is 6 - 2i, and the second endpoint is -4 + 6i.
Adding the real parts and the imaginary parts separately, we get (6 + (-4))/2 = 1 for the real part and ((-2) + 6)/2 = 2 for the imaginary part.
Therefore, the midpoint is given by 1 + 2i. This means that the midpoint of the segment lies on the complex plane at the coordinates (1, 2).
It represents the point equidistant from both endpoints, dividing the segment into two equal parts.
Learn more about Divide click here :brainly.com/question/28119824
#SPJ11
find the value of x in the proportion.
18/x = 9/7
Answers
Here you go
Hope this helps you
What is the distance between the points (19,-9) and (-5,-2)?
Answers
Answer:
look at image attached, hope this helps :)

James can read 520 words in 2 minutes and Luke can read 960 in 5 at what rates are james and Luke able to read?
Answers
please help me I dpnt know the answer and I dont want to do it

Answers
Answer:
the answer is -34
Step-by-step explanation:
the answer is n=34
A pizza maker determined an annual profit in dollars
2
from selling pizzas using f(n) = 65n -0.04n² where
n is the number of pizzas sold. What is the annual
profit if the pizza maker sells 300 pizzas?
A. $18,500
B. $3,600
C. $7,800
D. $15,900
Answers
Answer:
Given, the annual profit equation is f(n) = 65n - 0.04n².
When the number of pizzas sold, n = 300, the annual profit will be:
f(300) = 65(300) - 0.04(300)²
= 19500 - 0.04(90000)
= 19500 - 3600
= $15,900
Therefore, the annual profit if the pizza maker sells 300 pizzas is $15,900. Answer: D.
Step-by-step explanation:
What's the square root of 900
Answers
Step-by-step explanation:
30 im sure that ia the corect answer
Answer:
30
Step-by-step explanation:
i know this for a fact lmal
TRUE / FALSE. in our bstnode class the variables left and right, that represent the links of a node, are of class comparable.
Answers
in our bstnode class the variables left and right, that represent the links of a node, are of class comparable is FALSE.
The variables left and right in the bstnode class represent the links to the left and right subtrees of a node in a binary search tree. These variables are typically of the same type as the bstnode class itself, since they also represent nodes in the tree. They do not need to be of the class Comparable, as that interface is used for objects that can be compared to each other for the purposes of sorting. The bstnode class may contain an instance variable of a comparable type if the nodes are being sorted based on their values, but this is separate from the left and right variables. Conclusion: The variables left and right in the bstnode class are not of class Comparable.
To know more about variables visit:
brainly.com/question/29583350
#SPJ11
how many litres of milk can be put in six hemispherical bowl each of diameter 35cm
Answers
Answer:
Approximately 67.348 litres can be put in six hemispherical bowl with a diameter of 35 centimetres.
Step-by-step explanation:
The volume of a hemisphere (\(V\)), measured in cubic centimetres, is obtained from this formula:
\(V = \frac{2\pi}{3}\cdot R^{3}\)
Where \(R\) is the radius of the hemisphere, measured in centimetres.
We know that radius is the half of the diameter (\(D\)), measured in centimetres, then:
\(R = 0.5\cdot D\)
(\(D = 35\,cm\))
\(R = 0.5\cdot (35\,cm)\)
\(R = 17.5\,cm\)
Now, we get the volume of each hemispherical bowl:
\(V = \frac{2\pi}{3} \cdot (17.5\,cm)^{3}\)
\(V \approx 11224.649\,cm^{3}\)
The total volume of six hemispherical bowl is:
\(V_{T} = 6\cdot V\)
\(V_{T}= 6\cdot (11224.649\,cm^{3})\)
\(V_{T} = 67347.894\,cm^{3}\)
From Physics we know that 1 litre equals 1000 cubic centimetres. Then:
\(V_{T} = 67.348\,L\)
Approximately 67.348 litres can be put in six hemispherical bowl with a diameter of 35 centimetres.
(1 point) for the system of differential equations x′(t)=−95x 53y 2xy y′(t)=−185x 203y−xy
Answers
The given system of differential equations is:
x'(t) = -95x + 53y - 2xy
y'(t) = -185x - 203y - xy
To solve this system, we can use various methods such as substitution or matrix methods. Let's solve it using the matrix method.
We can rewrite the system of differential equations in matrix form as:
X' = AX
where X = [x y]', X' = [x'(t) y'(t)]', and A is the coefficient matrix:
A = [[-95 53], [-185 -203]]
To find the solutions, we need to find the eigenvalues and eigenvectors of matrix A. The eigenvalues are the roots of the characteristic equation det(A - λI) = 0, where I is the identity matrix. Solving this equation gives us the eigenvalues λ1 = -100 and λ2 = -198.
Next, we find the eigenvectors associated with each eigenvalue. For λ1 = -100, the corresponding eigenvector is [2 1]'. For λ2 = -198, the corresponding eigenvector is [-1 1]'.
Therefore, the general solution of the system of differential equations is:
X(t) = c1e^(-100t)[2 1]' + c2e^(-198t)[-1 1]'
where c1 and c2 are constants determined by initial conditions.
In summary, the solution to the system of differential equations is given by X(t) = c1e^(-100t)[2 1]' + c2e^(-198t)[-1 1]', where c1 and c2 are constants determined by the initial conditions.
Learn more about matrix method here: brainly.com/question/31504272
#SPJ11
NEED HELP!! Trigonometry questions

Answers
Answer:
Step-by-step explanation:
Question 1: Assumption: This is a 30-60-90 triangle.
Remember that the sides of a 30-60-90 triangle are in the ratio 1:√3:2
The side opposite the 90° angle is 16, so the side opposite the 30° angle is 16/2 = 8
x = 8 units.
:::::
Question 2: Assumption: This is an isosceles triangle.
Draw the altitude to the vertex angle and you get a 30-60-90 triangle.
The side opposite the 90° angle has length 22, so the side opposite the 30° angle has length 11.
x/2 = 11
x = 22 units
:::::
Question 3: Assumption: This is a 45-45-90 triangle.
The sides of a 45-45-90 triangle are in the ratio 1:1:√2
The sides opposite the 45° angles are 19 and x.
x = 19
:::::
Question 4: Assumption: This is an isosceles triangle.
x = 13 units
:::::
Question 5: Assumption: This is a right triangle.
sin(54°) = x/45
x = 45sin(54°) ≅ 36.4 units
:::::
Question 6: Assumption: This is a right triangle.
sin(35°) = z/23
z = 23sin(35°) ≅ 13.2 units

Which of the following best describes the power of the test described in question #6? a) Deciding that giving a gift encourages future donations when it really doesn't b) Deciding that giving a gift encourages future donations when it really does. c) Not deciding that giving a gift encourages future donations when it really doesn'ı d) Not deciding that giving a gift encourages future donations when it really does. c) None of these
Answers
Given that none of the provided options directly address the power of the test described, we can conclude that the answer is:
c) None of these.
The power of a test refers to the probability of correctly rejecting the null hypothesis when it is false. It measures the ability of a statistical test to detect a true effect or relationship.
The description of the power of the test cannot be determined based on the given options.
To know more about null hypothesis refer here
https://brainly.com/question/30821298#
#SPJ11
The ratios 4:12 and 11:x are equivalent. What is the value of x
Answers
Given the equivalent ratios:
4:12 and 11:x
To get an equivalent ratio, the denominator and numerator of one ratio is multiplied or divided by the same non zero number.
To find the value of x, we have:
\(\frac{4}{12}=\frac{11}{x}\)\(\begin{gathered} x=\frac{11\ast12}{4} \\ \\ x=33 \end{gathered}\)The value of x = 33
ANSWER:
33
Kyd and North are playing a game. Kyd selects one card from a standard 52-card deck. If Kyd selects a face card (Jack, Queen, or King). North pays him $5. If Kyd selects any other type of card, he pays North $2 a) What is Kyd's expected value for this game? Round your answer to the nearest cent. $ b) What is North's expected value for this game? Round your answer to the nearest cent. $ c) Who has the advantage in this game? North Box 1: Enter your answer as an integer or decimal number. Examples: 3,-4, 5.5172 Enter DNE for Does Not Exist, oo for Infinity Box 2: Enter your answer as an integer or decimal number. Examples: 3, 4, 5.5172 Enter DNE for Does Not Exist, oo for Infinity Box 3: Select the best answer Post this question to forum
Answers
Thus, we get the final values here as:
a) -0.38b) 0.38c) NorthHow to solvea. For Kyd, we are given here the gain and loss probabilities as:
P(X=5) = 3/13 as all the 3 face cards are equally likely as any of the 13 ranks of the cards.
For the losing outcome, we have here:
P(X=-2) = 10/13 as we lose 2 in all the other ranks here.
Therefore the expected value here is computed as:
Summation of X = 15/13 - 20/13 = -5/13 = -0.38
Therefore, -0.38 is the required expected value here.
Every 3 of the 13 ranks are face ranks and thus, the probability for getting a face card is given as:
b) As this is a zero sum game, the expected value for the other person would be the negative of the expected value for Kyd here. This is computed here as 0.38.
Therefore, 0.38 is the expected value here.
c) Clearly North has an advantage here.
Read more about probabilities here:
https://brainly.com/question/24756209
#SPJ1
commuting times for employees of a local company have a mean of 63.6 minutes and astandard deviation of 2.5 minutes. what does chebyshev's theorem say about thepercentage of employees with commuting times between 58.6 minutes and 68.6 minutes?
Answers
According to Chebyshev's theorem, at least 75% of the employees will have commuting times that fall within 2 standard deviations of the mean, or between 58.6 minutes and 68.6 minutes.
Chebyshev's theorem states that for any set of data, regardless of its distribution, a certain percentage of the data lies within a certain number of standard deviations from the mean. Specifically, Chebyshev's theorem states that for any data set, at least 1 – 1/k² of the data values will lie within k standard deviations of the mean, where k is any number greater than 1. If k=2, at least 75% of the data values lie within 2 standard deviations of the mean. If k=3, at least 89% of the data values lie within 3 standard deviations of the mean.
Therefore, for a data set with a mean of 63.6 minutes and a standard deviation of 2.5 minutes, we can use Chebyshev's theorem to determine that at least 75% of the employees will have commuting times that fall within 2 standard deviations of the mean, or between 58.6 minutes and 68.6 minutes.
Learn more abut Chebyshev's theorem here: https://brainly.com/question/5179184
#SPJ11
(a) Determine a cubic polynomial with integer coefficients which has $\sqrt[3]{2} + \sqrt[3]{4}$ as a root.
(b) Prove that $\sqrt[3]{2} + \sqrt[3]{4}$ is irrational.
Answers
Answer:
(a) \(x\³ - 6x - 6\)
(b) Proved
Step-by-step explanation:
Given
\(r = $\sqrt[3]{2} + \sqrt[3]{4}$\) --- the root
Solving (a): The polynomial
A cubic function is represented as:
\(f = (a + b)^3\)
Expand
\(f = a^3 + 3a^2b + 3ab^2 + b^3\)
Rewrite as:
\(f = a^3 + 3ab(a + b) + b^3\)
The root is represented as:
\(r=a+b\)
By comparison:
\(a = $\sqrt[3]{2}\)
\(b = \sqrt[3]{4}$\)
So, we have:
\(f = ($\sqrt[3]{2})^3 + 3*$\sqrt[3]{2}*\sqrt[3]{4}$*($\sqrt[3]{2} + \sqrt[3]{4}$) + (\sqrt[3]{4}$)^3\)
Expand
\(f = 2 + 3*$\sqrt[3]{2*4}*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4\)
\(f = 2 + 3*$\sqrt[3]{8}*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4\)
\(f = 2 + 3*2*($\sqrt[3]{2} + \sqrt[3]{4}$) + 4\)
\(f = 2 + 6($\sqrt[3]{2} + \sqrt[3]{4}$) + 4\)
Evaluate like terms
\(f = 6 + 6($\sqrt[3]{2} + \sqrt[3]{4}$)\)
Recall that: \(r = $\sqrt[3]{2} + \sqrt[3]{4}$\)
So, we have:
\(f = 6 + 6r\)
Equate to 0
\(f - 6 - 6r = 0\)
Rewrite as:
\(f - 6r - 6 = 0\)
Express as a cubic function
\(x^3 - 6x - 6 = 0\)
Hence, the cubic polynomial is:
\(f(x) = x^3 - 6x - 6\)
Solving (b): Prove that r is irrational
The constant term of \(x^3 - 6x - 6 = 0\) is -6
The divisors of -6 are: -6,-3,-2,-1,1,2,3,6
Calculate f(x) for each of the above values to calculate the remainder when f(x) is divided by any of the above values
\(f(-6) = (-6)^3 - 6*-6 - 6 = -186\)
\(f(-3) = (-3)^3 - 6*-3 - 6 = -15\)
\(f(-2) = (-2)^3 - 6*-2 - 6 = -2\)
\(f(-1) = (-1)^3 - 6*-1 - 6 = -1\)
\(f(1) = (1)^3 - 6*1 - 6 = -11\)
\(f(2) = (2)^3 - 6*2 - 6 = -10\)
\(f(3) = (3)^3 - 6*3 - 6 = 3\)
\(f(6) = (6)^3 - 6*6 - 6 = 174\)
For r to be rational;
The divisors of -6 must divide f(x) without remainder
i.e. Any of the above values must equal 0
Since none equals 0, then r is irrational
Consider the quadratic polynomial ax 2 bx c. suppose the coefficients are given by rolling a fair die three times. what is the probability that the roots of the polynomial are equal?
Answers
Complete the square to write
ax² + bx + c = a (x + b/(2a))² - (b² - 4ac)/(4a)
The quadratic has a double root at x = -b/(2a) if the constant term (b² - 4ac)/(4a) vanishes, which happens if b² - 4ac = 0.
Let A, B, and C be random variables representing the value of the first, second, and third roll of the die. They are independent and identically distributed with PMF
Pr [X = x] = 1/6
if x ∈ {1, 2, 3, 4, 5, 6}, and 0 otherwise.
We want to find
Pr [B² - 4AC = 0]
Note that
B² - 4AC = 0 ⇒ B² = 4AC ⇒ (B/2)² = AC
which tells us that B must be even, and also that AC is a perfect square. Then there are 5 possible outcomes that satisfy the conditions:
• If B = 2, then AC = 1 ⇒ A = C = 1
• If B = 4, then AC = 4 ⇒ A = 1, C = 4 or A = C = 2 or A = 4, C = 1
• If B = 6, then AC = 9 ⇒ A = C = 3
and there are 6³ = 216 total possible outcomes in the sample space. So,
Pr [B² - 4AC = 0] = 5/216
find the probability of spinning a 5 or a 4. write your answer as a decimal using the appropriate rounding rule.
Answers
The probability of spinning a 5 or a 4 is 0.2 or 20%.
To find the probability of spinning a 5 or a 4, you'll need to follow these steps:
1. Determine the total number of possible outcomes when spinning. For example, if the spinner has 10 equally spaced sections numbered 1 through 10, there are 10 possible outcomes.
2. Identify the number of successful outcomes, which are the ones with a 5 or a 4. In this case, there are 2 successful outcomes (spinning a 4 or a 5).
3. Calculate the probability by dividing the number of successful outcomes by the total number of possible outcomes. In this example, the probability would be:
Probability = (Number of successful outcomes) / (Total number of possible outcomes) = 2/10
4. To express this probability as a decimal, divide the numerator (2) by the denominator (10). The result is:
Decimal probability = 2 ÷ 10 = 0.2
5. Apply the appropriate rounding rule, if necessary. In this case, the decimal probability (0.2) is already in its simplest form, so no rounding is needed.
Learn more about probability here:
brainly.com/question/30034780
#SPJ11
I just need the answers please and thank you.

Answers
Answer:
1.) .423
2.).602
3.) .675
4.) .375
5.) .259
6.)8.144
7.).839
8.).017
9.) .966
10.).454
11.).978
12.) 57.28996
13.).5299
14.).809
15.).9004
16.).819
17.).788
18.) 1.235
Basically just change your calculator to degree by pressing the mode button then scroll to degree and pressing it. Then type the questions in with the cos tan and. Sin buttons and that’s the answer.
80) the referee awards a free kick. an opponent stands in front of the ball. play is restarted and the ball hits the opponent who is less than 10 yards from the ball. what decision should the referee make?
Answers
If an opponent stands less than 10 yards from the ball when a free kick is awarded, and the ball subsequently strikes that opponent, the referee should award an indirect free kick to the opposing team.
This is because the opponent is in violation of the laws of the game, specifically Law 13 - Free kicks which states that at a direct free kick, a player must be at least 10 yards (9.15m) from the ball until it is in play.
The indirect free kick should be taken from the spot where the opponent was when they were struck by the ball.
To learn more about Free Kicks
Visit; brainly.com/question/15700827
#SPJ4
Find the weighted average of these values. Value Weight 2.002.00 75.0u.0% 3.003.00 15.0.0% 4.004.00 10.0%
Answers
The reported values have a weighted average of 2.35.
Given the following data:
Value Weight
2.00 75.0%
3.00 15.0%
4.00 10.0%
The weighted average of these figures is calculated as follows:
First, multiply each value by its corresponding weight in decimal form and then add up the products:
2.00 * 0.75 + 3.00 * 0.15 + 4.00 * 0.10 = 1.50 + 0.45 + 0.40 = 2.35.
dividing the outcome by the weighted average:
2.35 ÷ (0.75 + 0.15 + 0.10) = 2.35 ÷ 1.00 = 2.35.
Know more about Weighted average here:
https://brainly.com/question/28334973
#SPJ11