Find the original price of a pair of gloves that is on sale for $28, a 30% discount from the original price.
Answers
Answer:
$8.40
Step-by-step explanation:
Answer:36.4
Step-by-step explanation:
Related Questions
Where do the lines y = 3x + 5 and y = -2x + 10 intersect?
Answers
9514 1404 393
Answer:
(x, y) = (1, 8)
Step-by-step explanation:
A graphing calculator quickly tells you the point of intersection.
__
You can equate the y-values and solve for x.
3x +5 = -2x +10
5x = 5 . . . . . . . . . add 2x-5
x = 1 . . . . . . . divide by 5
3·1 +5 = y = 8 . . . . substitute for x in the first equation
The point of intersection is (x, y) = (1, 8).

To pass a math test students must correctly answer at least 0.6 of the questions. Donald score is 5/8, Karen score is 0.88 Geno score is 3/5, and Ciara score is 4/5. how many of the students pass the test?
Answers
Answer:
To pass the test, a student must correctly answer at least 0.6 or 60% of the questions.
Donald's score is 5/8, which can be simplified to 0.625. Since this is greater than 0.6, Donald passes the test.
Karen's score is 0.88, which is greater than 0.6, so Karen passes the test.
Geno's score is 3/5, which can be simplified to 0.6. Since this is equal to 0.6, Geno passes the test.
Ciara's score is 4/5, which can be simplified to 0.8. Since this is greater than 0.6, Ciara passes the test.
Therefore, all the students pass the test.
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
Find the distance between point P and line L

Answers
The distance between point P and line L is 16/9√(13).
To find the distance between point P and line L, we can use the formula for the distance between a point and a line in two-dimensional space. The formula is as follows:
Let P = (x1, y1) be the point and L be the line ax + by + c = 0. Then the distance between P and L is:
|ax1 + by1 + c|/√(a² + b²)
To find a, b, and c for the given line, we need to put it in slope-intercept form y = mx + b by solving for y.
2x - 3y = 12=> 2x - 12 = 3y=> (2/3)x - 4 = y
The slope of the line, m, is the coefficient of x, which is 2/3. Therefore, the line is:
y = (2/3)x - 4The values of a, b, and c are: a = 2/3b = -1c = -4
Now we can substitute the coordinates of P and the values of a, b, and c into the formula for the distance between a point and a line.
Let P = (3, 5).|a(3) + b(5) + c|/√(a² + b²)= |(2/3)(3) - 1(5) - 4|/√[(2/3)² + (-1)²]= |-4/3 - 4|/√(4/9 + 1)= 16/9√(13).
for such more questions on distance
https://brainly.com/question/30395212
#SPJ8
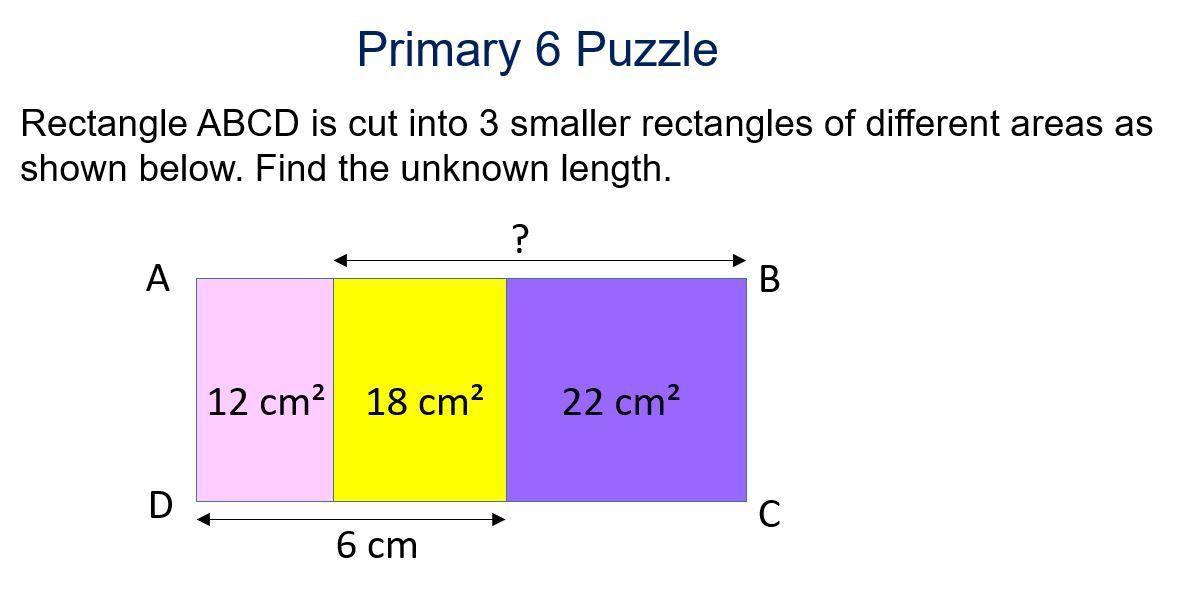
May any kind soul teach me on how to do this primary six math question .
Answers
The unknown length in the rectangle is ? = 8cm
How to find the unknown length?We we want to find the unknown length.
First, if we look just at the pink and yellow rectangles we can see that these have a combined area of:
A = 12cm² + 18cm²
A = 30cm²
And we know that one side measures 6cm, then the length of AD is:
AD*6cm = 30cm²
AD = 30cm²/6cm
AD = 5cm
Now, the yellow and purple rectangles have a combined area of:
A = 18cm² + 22cm² = 40cm²
Then we can write:
?*AD = 40cm²
?*5cm = 40cm²
? = 40cm²/5cm
? = 8cm
That is the unknown lenght.
Learn more about area at:
https://brainly.com/question/24487155
#SPJ1
Find the 9th term of the geometric sequence 8,32,128,
Answers
\(\text{First term,}~ a = 8\\\\\text{Common ratio,}~ r= \dfrac{32}8 = 4\\\\\text{nth term} = ar^{n-1} \\\\\text{9th term} = 8\cdot 4^{9-1}\\\\\\~~~~~~~~~~~~~=8 \cdot 4^8\\\\\\~~~~~~~~~~~~~=524288\\\\\text{The 9th of the geometric sequence is 525288.}\)
Consider the line 5x+2y=−4. What is the equation of the line parallel to the given line that passes through the point (−2, 6) in slope-intercept form? Enter your answer by filling in the boxes to complete the equation.
Answers
Answer:
y = -5/2x +1
Step-by-step explanation:
You want the slope-intercept form equation for the line through the point (-2, 6) that is parallel to 5x +2y = -4.
Parallel lineThe equation of a parallel line can be the same as the given equation, except for the constant. The new constant can be found by substituting the given point coordinates:
5(-2) +2(6) = c
-10 +12 = c
2 = c
Now we know the equation of the parallel line can be written as ...
5x +2y = 2
Slope-intercept formSolving for y puts this in slope-intercept form:
2y = -5x +2 . . . . . . . . subtract 5x
y = -5/2x +1 . . . . . . . . divide by 2
We don't know what your boxes look like, but we can separate the numbers to make it look like this:
\(\boxed{y=\dfrac{-5}{2}x+1}\)
#95141404393

Enter values to complete the table below.

Answers
For the given values of x and y, the value of y/x (that represents the slope of the equation) = 3/1, 3/1, 3
What does slope mean in math?A line's steepness can be determined by looking at its slope. Slope is calculated mathematically as "rise over run" (change in y divided by change in x).
The ratio of the increase in elevation between two points to the run in elevation between those same two points is referred to as the slope.
Given are the values of the x and y
y/x represents the slope of the equation,
for x = -1 and y = -3,
y/x = 3/1
for x = 1 and y = 3
y/x = 3/1
for x = 2 and y = 6
y/x = 6/2 = 3
To learn more about slope of the equation from given link
https://brainly.com/question/24907633
#SPJ10
Is F(X) =9 to x power a exponential decay?
Answers
Pls help I need this I’m begging you

Answers
Answer:
Option H
Step-by-step explanation:
y = 3x - 4
this is the correct answer.
Answer:
H- y=3x-4
The reason I answered this is because the equations are in slope-intercept format (y=mx+b), the slope(m), is 3. The y intercept(b) is -4. Hope this helped :)
The factors of a number are given below: 2, 4, 5, 8, 10, 16, 20, 40. What is the number?

Answers
Answer:
the answer would be 80 because it is divisible with all the numbers shown above
Graph the data below and then answer the questions that follow. year 1=$20,000, year 2=$21,750, year 3=$23,500, year 4=$25,250, year 5=$27,000. is this an arithmetic sequence? How do you know?
Answers
Answer:
Since the difference between the value for each year is constant, this is an arithmetic sequence.
Step-by-step explanation:
Year 2 - Year 1 = 21,750 - 20,000 = 1,750
Year 3 - Year 2 = 23,500 - 21,750 = 1,750
Year 4 - Year 3 = Year 5 - Year 4 = 1,750
Show that the equations x+y+z = 4, 2x+5y-2z =3, x+7y-7z =5 are not consistent
Answers
Answer:
We can start by using the second equation to eliminate x:
2x + 5y - 2z = 3
2x = -5y + 2z + 3
x = (-5/2)y + z + 3/2
Now we can substitute this expression for x into the first and third equations:
x + y + z = 4
(-5/2)y + z + 3/2 + y + z = 4
(-5/2)y + 2z = 5/2
x + 7y - 7z = 5
(-5/2)y + z + 3/2 + 7y - 7z = 5
(9/2)y - 6z = 7/2
Now we have a system of two equations with two variables, (-5/2)y + 2z = 5/2 and (9/2)y - 6z = 7/2. We can use any method to solve for y and z, such as substitution or elimination. However, we will find that the system is inconsistent, meaning there is no solution that satisfies both equations.
Multiplying the first equation by 9 and the second equation by 5 and adding them, we get:
(-45/2)y + 18z = 45/2
(45/2)y - 30z = 35/2
Adding these two equations, we get:
-12z = 40/2
-12z = 20
z = -5/3
Substituting z = -5/3 into (-5/2)y + 2z = 5/2, we get:
(-5/2)y + 2(-5/3) = 5/2
(-5/2)y - 10/3 = 5/2
(-5/2)y = 25/6
y = -5/12
Substituting y = -5/12 and z = -5/3 into any of the original equations, we get:
x + y + z = 4
x - 5/12 - 5/3 = 4
x = 29/12
Therefore, the solution is (x, y, z) = (29/12, -5/12, -5/3). However, if we substitute these values into any of the original equations, we will find that it does not satisfy the equation. For example:
2x + 5y - 2z = 3
2(29/12) + 5(-5/12) - 2(-5/3) = 3
29/6 - 5/2 + 5/3 ≠ 3
Since there is no solution that satisfies all three equations, the system is inconsistent.
Step-by-step explanation:
Answer:
See below for proof.
Step-by-step explanation:
A system of equations is not consistent when there is no solution or no set of values that satisfies all the equations simultaneously. In other words, the equations are contradictory or incompatible with each other.
Given system of equations:
\(\begin{cases}x+y+z = 4\\2x+5y-2z =3\\x+7y-7z =5\end{cases}\)
Rearrange the first equation to isolate x:
\(x=4-y-z\)
Substitute this into the second equation to eliminate the term in x:
\(\begin{aligned}2x+5y-2z&=3\\2(4-y-z)+5y-2z&=3\\8-2y-2z+5y-2z&=3\\-2y-2z+5y-2z&=-5\\5y-2y-2z-2z&=-5\\3y-4z&=-5\end{aligned}\)
Subtract the first equation from the third equation to eliminate x:
\(\begin{array}{cccrcrcl}&x&+&7y&-&7z&=&5\\\vphantom{\dfrac12}-&(x&+&y&+&z&=&4)\\\cline{2-8}\vphantom{\dfrac12}&&&6y&-&8z&=&1\end{aligned}\)
Now we have two equations in terms of the variables y and z:
\(\begin{cases}3y-4z=-5\\6y-8z=1\end{cases}\)
Multiply the first equation by 2 so that the coefficients of the variables of both equations are the same:
\(\begin{cases}6y-8z=-10\\6y-8z=1\end{cases}\)
Comparing the two equations, we can see that the coefficients of the y and z variables are the same, but the numbers they equate to is different. This means that there is no way to add or subtract the equations to eliminate one of the variables.
For example, if we subtract the second equation from the first equation we get:
\(\begin{array}{crcrcl}&6y&-&8z&=&-10\\\vphantom{\dfrac12}-&(6y&-&8z&=&\:\:\;\;\:1)\\\cline{2-6}\vphantom{\dfrac12}&&&0&=&-11\end{aligned}\)
Zero does not equal negative 11.
Since we cannot eliminate the variable y or z, we cannot find a unique solution that satisfies all three equations simultaneously. Therefore, the system of equations is inconsistent.
You deposit $5000 in an account earning 5% interest compounded continuously. How much will you have in the account in 5 years? Round to the nearest cent.
Answers
The admission fee at a local zoo is $1.50 for children and $5.00 for adults. On a certain day, 3000 people enter the zoo and $9, 400.00 is collected. How many children and how many adults attended?
Answers
1600 children and 1400 adults attended
How to determine the number of adults?Let the children be x and adult be y.
So, we have the following equations:
x + y = 3000
1.5x + 5y = 9400
Make x the subject in x + y = 3000
x = 3000 - y
Substitute x = 3000 - y in 1.5x + 5y = 9400
1.5(3000 - y) + 5y = 9400
Expand
4500 - 1.5y + 5y = 9400
Evaluate the like terms
3.5y = 4900
Divide both sides by 3.5
y = 1400
Substitute y = 1400 in x = 3000 - y
x = 3000 - 1400
Evaluate
x = 1600
Hence, 1600 children and 1400 adults attended
Read more about system of equations at:
https://brainly.com/question/14323743
#SPJ1
easy math only shapes

Answers
ineed20morewordstouploadthisandyesitseasymatj
Answer:
Hello your answer would be A
Step-by-step explanation:
hev nice day
[o]-[o]
\__/
Answer the Both (a) and (b) . And show the method too. I will make Brainelist + 50 points

Answers
#a
4p-6pq+9q-64p-3(2pq+3q-2)#b
That be x and y
So
x+y=15--(1)2x+4y=64--(2)So
from eq(1)
x=15-y--(3)Put in second one
2(15-y)+4y=6430-2y+4y=642y=34y=17Put in third one
x=15-17x=-2Take it positive
x=2Answer:
(a) (i) Factorize \(\sf 4p-6pq+9q-6\)
Rewrite by swapping the order of the first two terms:
⇒ -6pq + 4p + 9q - 6
Factorize the first two terms and the last two terms separately:
⇒ -2p(3q - 2) + 3(3q - 2)
Factor out the common term (3q - 2):
⇒ (3q - 2)(-2p + 3)
(ii)
Square of the binomial: \((a+b)^2=a^2+2ab+b^2\)
Rewrite \(9.9\) as \(10 - 0.1\)
Therefore, \(a = 10\) and \(b = -0.1\)
Also, remember that multiplying a number by 0.1 is the same as dividing it by 10. (when dividing a decimal number by 10, simply move the decimal point 1 place to the left).
\(\begin{aligned}\implies 9.9^2 & =(10-0.1)^2\\ & =10^2-2 \cdot 10 \cdot 0.1+0.1^2\\& = 100-\dfrac{2 \cdot 10}{10}+\dfrac{0.1}{10}\\& =100-2+0.01\\ & =98 + 0.01\\ & = 98.01\end{aligned}\)
(b) (i)
Let x = number of motor bicycles
Let y = number of cars
Given:
There are 15 vehicles of two types⇒ x + y = 15
Given:
The number of tires in all vehicles is 64- Motor bicycles have 2 tires each
- Cars have 4 tires each
⇒ 2x + 4y = 64
(ii) Rewrite x + y = 15 to make x the subject:
⇒ x = 15 - y
Substitute into 2x + 4y = 64 and solve for y:
⇒ 2(15 - y) + 4y = 64
⇒ 30 - 2y + 4y = 64
⇒ 30 + 2y = 64
⇒ 2y = 34
⇒ y = 17 cars
Substitute found value of y into x = 15 - y to find x:
⇒ x = 15 - 17 = -2 motorbikes
**There must be an error in the question, as with the given information, the number of motorbikes is -2, which is impossible.**
Here are the possible combinations of number of motorbikes (M) and number of cars (C) whose sum of tires is 64. As you can see, there is no combination that sums to 15 vehicles:
0 M + 16 C = 16 vehicles
2 M + 15 C = 17 vehicles
4 M + 14 C = 18 vehicles
6 M + 13 C = 19 vehicles
8 M + 12 C = 20 vehicles
10 M + 11 C = 21 vehicles
12 M + 10 C = 22 vehicles
14 M + 9 C = 23 vehicles
16 M + 8 C = 24 vehicles
18 M + 7 C = 25 vehicles
20 M + 6 C = 26 vehicles
22 M + 5 C = 27 vehicles
24 M + 4 C = 28 vehicles
26 M + 3 C = 29 vehicles
28 M + 2 C = 30 vehicles
30 M + 1 C = 31 vehicles
32 M + 0 C = 32 vehicles
To prepare a solution of NaCl, you weigh out 2.634(±.002)g and dissolve it in a volumetric flask whose volume is 100.00(±0.08)ml. Express the molarity of the solution, along with its uncertainty, with an appropriate number of digit.
Answers
The molarity of the solution is (0.4507 ± 0.0007) M.
Molarity of a given solution is defined as the total number of moles of solute per litre of solution. The molality of a solution is dependent on the changes in physical properties of the system such as pressure and temperature as unlike mass, the volume of the system changes with the change in physical conditions of the system. Molarity is represented by M, which is termed as molar. One molar is the molarity of a solution where one gram of solute is dissolved in a litre of solution. As we know, in a solution, the solvent and solute blend to form a solution, hence, the total volume of the solution is taken.
Mass of NaCl = 2.634 ± 0.002 g
Molar mass of NaCl = 58.4430 g/mol
Volume = 100.00 ± 0.08 mL = 0.10000 ± 0.00008 L
Molarity = moles/volume = mass/(molar mass x volume)
= 2.634/(58.443 x 0.1000) = 0.45069555 M
Assuming no uncertainty/error in the molar mass,
%Error in molarity = %error in mass + %error in volume
= 100 x 0.002/2.634 + 100 x 0.08/100.00 = 0.16%
Absolute error in molarity = 0.16/100 x 0.45069555= 0.0007 M
So, Molarity = (0.4507 ± 0.0007) M
Therefore, the molarity of the solution is (0.4507 ± 0.0007) M.
For more such questions on Molarity
https://brainly.com/question/2817451
#SPJ4
Question 1-1
Barrett earns $15 per hour cutting grass and $10 per hour tutoring reading. In one month, Barrett needs to save at least $400 for a
new lawnmower but does not want to work more than 35 hours.
Part A: Let z represent the hours cutting grass and y represent the hours tutoring. Given z 20 and y ≥ 0, select all the inequalities
that represent the situation.
Answers
On solving the inequality we know, Barrett should work 25 hours tutoring and 10 hours cutting grass to make $400.
What exactly does inequality mean?In mathematics, "inequality" refers to a relationship between two expressions or values that is not equal to each other. Therefore, inequality results from a lack of balance.
Solution:-
given,
z=hours of cutting grass
y=hours of tutoring
Two equation can be made using given condition
15z+10y=400
and
z+y=35
Solving both equation simultaneously,
we get
y=25
z=10
To know more about inequality visit:-
brainly.com/question/28823603
#SPJ1
What happens if you can write a function as a composite in different ways? Do you get the same derivative each time? The Chain Rule says you should. Find
dy/dx if y=x by using the Chain Rule with y as a composite of the following functions. Complete parts (a) and (b) below.

Answers
Using the Chain Rule, we have: dy/dx = f'(g(x)) * g'(x) = 1 * 1 = 1.The derivative of y with respect to x is 1.
When we compose a function, it may be possible to write it in a variety of different ways. Differentiating such functions can result in different derivatives, but the Chain Rule indicates that the derivatives of the compositions should be the same regardless of how the function is written, if the function is continuous and differentiable.For instance, consider the function f(x) = sin(x²). It can be written as f(g(x)) where g(x) = x² and f(x) = sin(x). Furthermore, it can be written as f(h(x)) where h(x) = x² and f(x) = sin(x). These are both compositions of functions, but they are different compositions that lead to different derivatives.However, if the function is a composite of differentiable functions, the Chain Rule tells us that the derivative of a composite function is the derivative of the outer function multiplied by the derivative of the inner function.
To find dy/dx if y = x using the Chain Rule with y as a composite of the following functions, we must first rewrite y as a composite function: y = f(g(x)) where g(x) = x and f(x) = x. This composite function can be written in a variety of different ways, such as y = f(h(x)) where h(x) = x and f(x) = x, or y = f(k(x)) where k(x) = x and f(x) = x. However, regardless of how we write it, the Chain Rule tells us that the derivative of y is equal to the derivative of the outer function (f(x) = x) multiplied by the derivative of the inner function (g(x) = x).
For more such questions on derivative
https://brainly.com/question/26369159
#SPJ8
When the suns rays are at an angle of 39° the distance from the top of Dakotas head to the tip of the shadow is 77 inches, about how tall is Dakota?
Answers
Answer:
48.45in
Step-by-step explanation:
To get the height of Dakota, we will use the SOH CAH TOA
Given the following
angle of elevation = 39degrees
distance from the top of Dakotas head to the tip of the shadow = 77in (Hyp)
Required
Height of Dakota (Opp)
Sin 39 = opposite/hyp
Sin39 = H/77
H = 77sin39
H = 77(0.6293)
H = 48.45in
Hence the Dakota is 48.45in
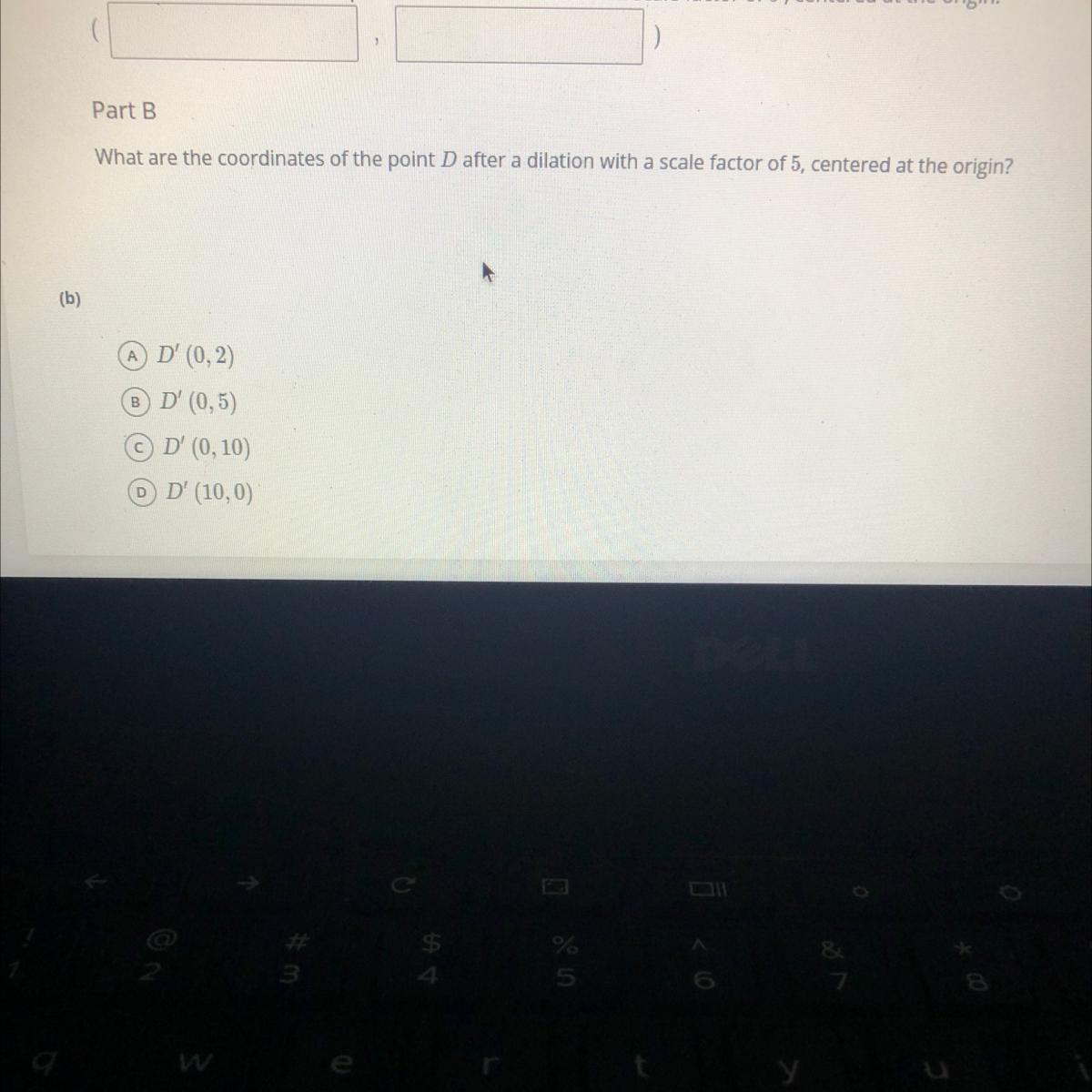
Write the coordinates of the point C after dilation with scale factor of 5, centered at the orgin
Answers
Answer:
It's C buddy
Step-by-step explanation:
Trying to solve this probelm i keep getting -10 -2(4x+4)-3x-2=34
Answers
Answer:
x= -4
Step-by-step explanation:
−2(4x+4)−3x−2=34
(−2)(4x)+(−2)(4)+−3x+−2=34(Distribute)
−8x+−8+−3x+−2=34
(−8x+−3x)+(−8+−2)=34(Combine Like Terms)
−11x+−10=34
−11x−10=34
−11x−10+10=34+10
−11x=44
−11x /−11 = 44 /−11
x=−4
Can someone please provide a step-by-step explanation for the answer?
If the universe of discourse is the real numbers, give the truth value of each of the
following propositions:
(a) ∀x∃y(x = y²)
(b) ∀x∃y(x² = y)
(c) ∃x∀y(xy = 0)
(d) ∀x∃y(x + y = 1)

Answers
The Propositions are resulting
(a) ∀x∃y(x = y²) is False
(b) ∀x∃y(x² = y) is True.
(c) ∃x∀y(xy = 0) is True.
(d) ∀x∃y(x + y = 1) is True.
(a) ∀x∃y(x = y²)
This proposition states that for every x, there exists a y such that x is equal to y². To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any positive value for x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4 = 2². Similarly, if x = 9, then y = 3 satisfies the equation since 9 = 3².
Therefore, the proposition (a) is false.
(b) ∀x∃y(x² = y)
For any given positive or negative value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4² = 2. Similarly, if x = -4, then y = -2 satisfies the equation since (-4)² = -2.
Therefore, the proposition (b) is true.
(c) ∃x∀y(xy = 0)
The equation xy = 0 can only be satisfied if x = 0, regardless of the value of y. Therefore, there exists an x (x = 0) that makes the equation true for every y.
Therefore, the proposition (c) is true.
(d) ∀x∃y(x + y = 1)
To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 2, then y = -1 satisfies the equation since 2 + (-1) = 1. Similarly, if x = 0, then y = 1 satisfies the equation since 0 + 1 = 1.
Therefore, the proposition (d) is true.
Learn more about Proposition here:
https://brainly.com/question/30695879
#SPJ1
Carlos deposits $400 into an account that pays simple interest at a rate of 6% per year. How much interest will he be paid in the first 6 years?
Answers
Answer:
hbjnmui,lhyjngrfdxw
Step-by-step explanation:
Quadrilateral ABCD is a square and the length of BD¯¯¯¯¯ is 10 cm.
What is the length of AE¯¯¯¯¯ ?
Enter your answer in the box.
the length of AE¯¯¯¯¯ =
cm
Answers
The length of AE¯¯¯¯¯ is 5√2 cm.
Since quadrilateral ABCD is a square, all four sides are congruent. Let's denote the length of one side as s. Therefore, the length of BD¯¯¯¯¯ is equal to s.
Given that the length of BD¯¯¯¯¯ is 10 cm, we can conclude that s = 10 cm.
Now, we need to find the length of AE¯¯¯¯¯. Looking at the square, AE¯¯¯¯¯ is the diagonal connecting opposite corners.
In a square, the diagonal divides the square into two congruent right triangles. We can use the Pythagorean theorem to find the length of the diagonal.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
In this case, the diagonal (the hypotenuse) is the same as the side length, s.
Applying the Pythagorean theorem:
s^2 = AE¯¯¯¯¯^2 + AE¯¯¯¯¯^2
10^2 = AE¯¯¯¯¯^2 + AE¯¯¯¯¯^2
100 = 2 * AE¯¯¯¯¯^2
AE¯¯¯¯¯^2 = 50
Taking the square root of both sides:
AE¯¯¯¯¯ = √50
Simplifying the square root:
AE¯¯¯¯¯ = √(25 * 2) = 5√2 cm
for more such questions on quadrilateral
https://brainly.com/question/27991573
#SPJ8
Kimberly has 500 in a savings account at the beginning of the summer. She wants to have at least $200 in the account at the end of the summer. He withdraws $ 25 each week for food, clothes, and movie tickets. How many weeks can Kimberly withdraw money and still have $200 in her account at the end of the summer?
Answers
Answer:
Step-by-step explanation:
The inequality is 500 - 25x >= 200
This insures that he will have at least 200 at the end of the summer.
subtract 200 from both sides of that inequality and add 25x to both sides of that inequality to get 500 - 200 >= 25x
simplify to get 300 >= 25x
divide both sides of that equation by 25 to get 300 / 25 >= x
simplify to get 12 >= x 12 >= x means x <= 12.
Answer: Let's start by figuring out how much money Kimberly will have left at the end of the summer if she withdraws $25 each week.
Since there are 12 weeks in the summer, she will withdraw a total of:
$25 x 12 = $300
So if she starts with $500, she will have:
$500 - $300 = $200
left at the end of the summer.
Therefore, Kimberly can withdraw money for up to 12 weeks and still have $200 in her account at the end of the summer.
Step-by-step explanation:
Jenna can type 140 words in 4 minutes. If she needs to type 385 words, how long would this take her? Explain how you got your answer
Answers
Answer:
11 minutes
Step-by-step explanation:
Because she types only 140 words in 4 minutes so if you add
140+140=280
if you divide
140/4 you get 35
so every minute she types in 35 words. So multiply
11 times 35 and you exactly get 385.
Answer:
11 min
Step-by-step explanation:
140 ÷ 4
= 35 which is the amount of words that she types in 1 min.
385 ÷ 35
= 11
so it will take Jenna 11 min to type 385 words.
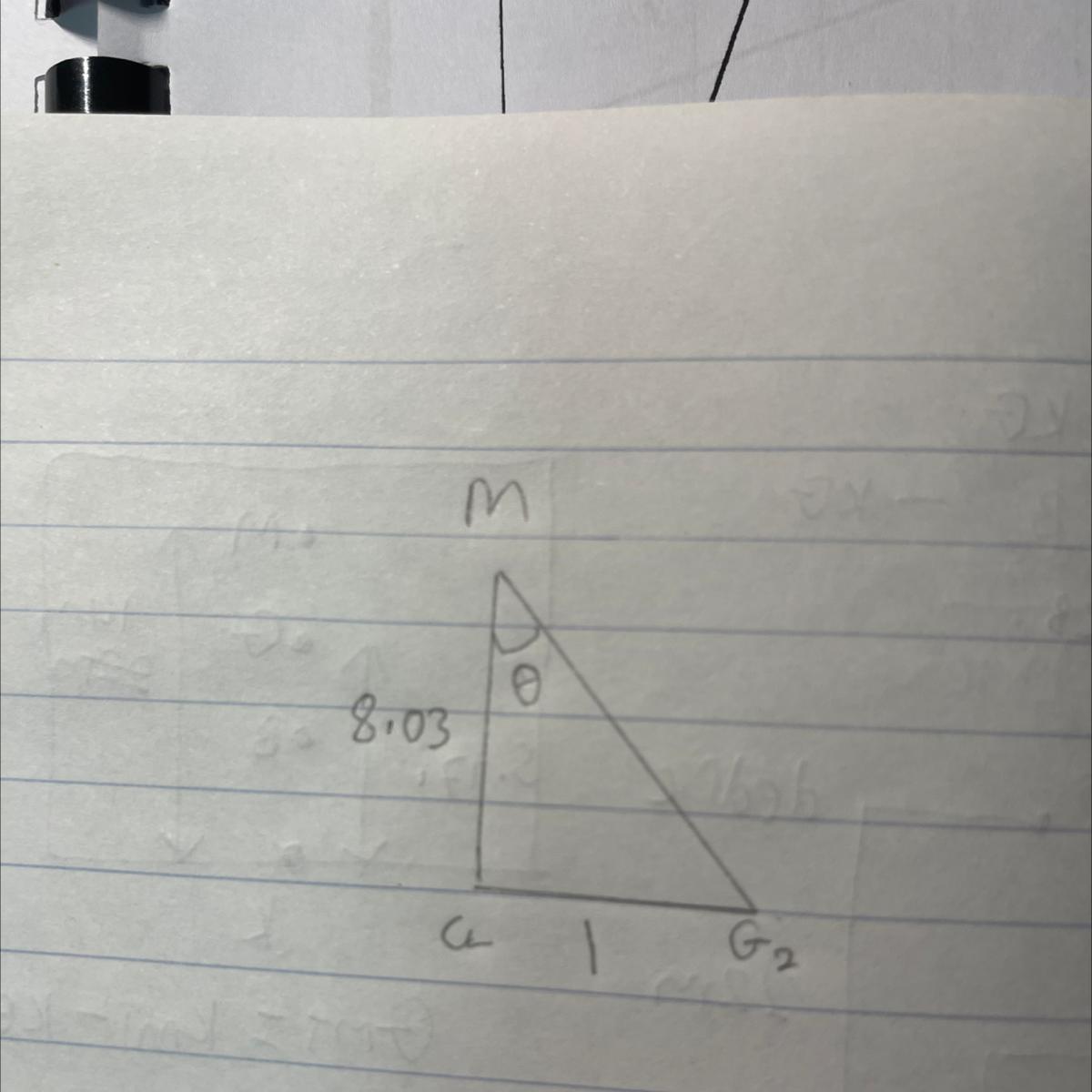
How to find the angle ? Help pls
Answers
Answer:
I got :
Angle theta = 7.1° (approximately)Step-by-step explanation:
see attached photo

Step-by-step explanation:
The angle of an equilateral triangle is 180°, and its three internal angles are equal, all being 60°.
Is (-2, 10) a solution to this system of equations?
y = -4x + 2
y = -6x - 2
yes
no
Answers
To find the look at the following procedures
Y=-4x+2
Let -2 be x and 10 be y
10=-4(-2)+2
10=8+2
10=10
For the second equation
Y=-6x-2
10=-6(-2)-2
10=12-2
10=10
Please give me branliest please
Answer:
Yes
Step-by-step explanation:
(-2, 10)
x = -2
y = 10
y = -4x + 2
Substitute or plug in the x and y values
10 = -4(-2) + 2
Multiply(remember a negative times a negative is a positive)
10 = 8 + 2
Add
10 = 10
Because ten is equal to ten (-2, 10) is a solution for this part
Now take your next equation and repeat the same steps
y = -6x - 2
10 = -6(-2) - 2
10 = 12 -2
10 = 10
(-2, 10) is a solution to this system of equations