Find the measure of the missing angles. Need help ASAP
Answers
Answer:
I don't see the photo. Can't help OOF
Step-by-step explanation:
Related Questions
Please help I don’t understand this

Answers
Answer:
The area is 24
Step-by-step explanation:
Divide the quadrilateral into 4 triangles (two identical at the top and two identical at the bottom).
Then find the area of each triangle and add it all together
Area of Triangle= (base x height)/2
(3 x 3)/2 + (3 x 3)/2 + (5 x 3)/2 + (5 x 3)/2
this equation gives us 24 as the area
pls help me!!! I WILL GIVE BRAINLIEST!!!!!! probability question

Answers
Answer:
B
Step-by-step explanation:
0 to 9 has 10 numbers, and 7 numbers are 0, 1, 2, 3, 4, 5, 6, so the ans is B.
---------------------------------------------------------------------------------------
Hope this helps you...
Dima has twice as many books as Ramiro. If dima gives 12 books to Ramiro, they will have the same number of books.How many books do they have in total
Answers
Answer:
They have 36 books in total.
Step-by-step explanation:
Let d = The number of Dima's books
Let r = The number of Ramiro's books.
d = 2r
d - 12 = r Substitute 2r for d in the second equation and solve for r
2r - 12 = r Subtract 2r from both sides
2r - 2r - 12 = r - 2r
-12 = -r Multiply both sides by -1
12 = r
Ramiro has 12 books.
d = 2r substitute 12 for r and solve for d
d = 2(12)
d = 24
Dima has 24 books.
Together they have 36 books (12 + 24)
Helping in the name of Jesus.
Answer:36
Step-by-step explanation:
Jessica has eaten 3 1/2 hot dogs of the 10 hot dogs she
recently found in her freezer. What percent of the hot
dogs has she eaten?
Answers
Answer:
65%
Step-by-step explanation:
100%-> 10
1%->0.1
----------------------------
10 - 3 1/2 = 6 1/2
6 1/2 ÷ 0.1 = 65
Find the area of the shaded region

Answers
Answer:
128 centimeter
Step-by-step explanation:
sana makatulong
Choose a linear function for the line represented by the point-slope equation y – 5 = 3(x – 2).
Answers
The Linear function for the line represented by the point-slope equation y - 5 = 3(x - 2) is y = 3x - 1.
The point-slope equation for a line is of the form y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope of the line. Given the point-slope equation y - 5 = 3(x - 2),
we can see that the slope of the line is 3 and it passes through the point (2, 5).
To find the linear function for the line, we need to write the equation in slope-intercept form, which is y = mx + b, where m is the slope of the line and b is the y-intercept (the point at which the line intersects the y-axis).
To get the equation in slope-intercept form, we need to isolate y on one side of the equation.
We can do this by distributing the 3 to the x term:y - 5 = 3(x - 2) y - 5 = 3x - 6 y = 3x - 6 + 5 y = 3x - 1
Therefore, the linear function for the line represented by the point-slope equation y - 5 = 3(x - 2) is y = 3x - 1.
For more questions on Linear .
https://brainly.com/question/2030026
#SPJ8
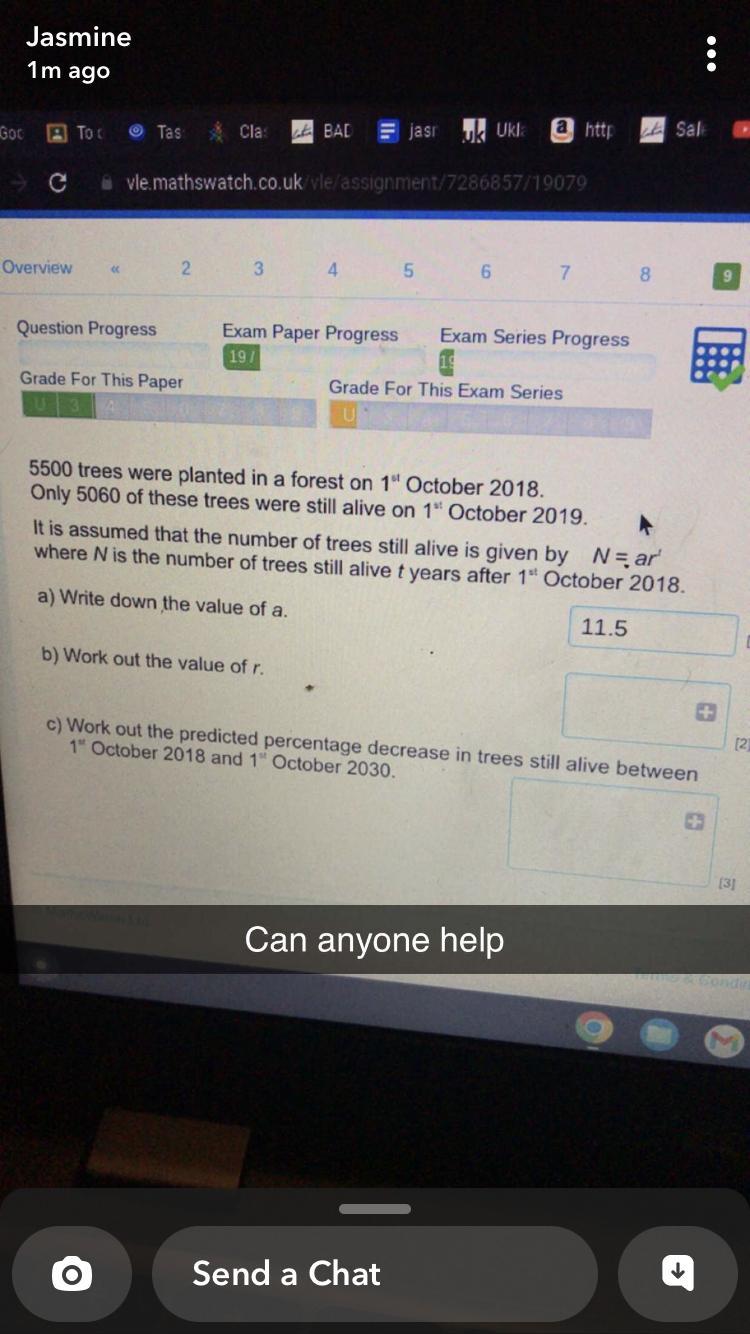
5500 trees were planted on 1st october 2018 only 5060 trees were alive on 1st october 2019 it is assumed that the number of trees alive is given by N = ar where N is the number of trees still alive t years after October 1 2018 What is the value of a
Answers
Considering the information about trees, The value of a is 5500
The value of r is calculated to be 0.92
In 1 October 2030 the number is 2022
How to find the value of aA mathematical function called an exponential function is employed frequently in everyday life. It is mostly used to compute investments, model populations, determine exponential decay or exponential growth, and so on.
Exponential function is a type of function of the form: f(x) = a(b)^x. It is made up of 3 main parts
a = the starting or initial value
b = the base function
x = the exponents
Considering the given problem, N = ar^t
the starting, a = 5500
the base, r =
the exponents = t
Solving for the base
N = ar^t
5500 = ar^t in 2018 t = 0
a = 5500
in 2019, t = 1
N = ar^t
5060 = 5500 * r
r = 5060/5500
r = 0.92
From 2018 to 2030 = 12 years, hence t = 12
N = 5500 * 0.92^12
N = 2,022.165132
N = 2022
Learn more about exponential function here:
https://brainly.com/question/29716012
#SPJ1
Simplify :
−5/4÷2 3/5
Answers
Answer:
-25/52
Step-by-step explanation:
that's what I got.
can someone help please

Answers
Answer:
1.6
Step-by-step explanation:
The expression: not X and Y
is true if X is false and Y is true
ture of false
Answers
TRUE. The expression "not X and Y" is a conjunction of two logical statements, where "not X" is the negation of X, and "Y" is another logical statement.
In general, the truth value of a conjunction is only true when both statements are true. In this case, if X is false (i.e., not true) and Y is true, then "not X" is true and "Y" is also true. Therefore, "not X and Y" is true in this case.
The expression "not X and Y" can be represented using truth tables, which are tables that show the possible combinations of truth values for the logical statements involved, and the resulting truth values of the expression.
To learn more about logical statement please click on below link.
https://brainly.com/question/18575348
#SPJ4
The expression: not X and Y is true if X is false and Y is true? TRUE of FALSE.
PLEASE ANSWER IT QUICKLY

Answers
Find the solution of the initial-value problem -7 83 y"-6y" +25y-150y=sec 5t, y(0) = 2, y/(0) = = ." (0) 2 2 A fundamental set of solutions of the homogeneous equation is given by the functions: 3/₁
Answers
The solution to the given initial-value problem -7y" + 83y' - 6y" + 25y - 150y = sec(5t), y(0) = 2, and y'(0) = 2 is y(t) = 3/4 - 2/3e^(6t/7) + (3/7)sec(5t).
To solve the given initial-value problem, we first find the solution to the associated homogeneous equation -7y" + 83y' - 6y" + 25y - 150y = 0. The characteristic equation is -7r² + 83r - 6 = 0, which can be factored as (-r + 2)(7r - 3) = 0. This gives us two roots, r₁ = 2/7 and r₂ = 3/7.
Using the fundamental set of solutions for the homogeneous equation, we have y_h(t) = C₁e^(2t/7) + C₂e^(3t/7), where C₁ and C₂ are constants.
To find the particular solution for the given non-homogeneous term sec(5t), we can use the method of undetermined coefficients. We assume a particular solution of the form y_p(t) = Asec(5t), where A is a constant to be determined.
Differentiating y_p(t), we find y_p'(t) = 5Asec(5t)tan(5t) and y_p"(t) = 5A(5sec²(5t)tan(5t) + sec²(5t)).
Substituting these into the original equation, we get -7(5A(5sec²(5t)tan(5t) + sec²(5t))) + 83(5Asec(5t)tan(5t)) - 6(5Asec²(5t)tan(5t) + sec²(5t)) + 25(Asec(5t)) - 150(Asec(5t)) = sec(5t).
Simplifying the equation, we find -35Asec²(5t) + 415Asec(5t) = sec(5t).
Equating the coefficients of sec²(5t) and sec(5t) on both sides, we get -35A = 0 and 415A = 1. Solving for A, we find A = 1/415.
Therefore, the particular solution is y_p(t) = (1/415)sec(5t).
The general solution is the sum of the homogeneous and particular solutions: y(t) = y_h(t) + y_p(t) = C₁e^(2t/7) + C₂e^(3t/7) + (1/415)sec(5t).
Using the initial conditions y(0) = 2 and y'(0) = 2, we can solve for C₁ and C₂, and substitute the values back into the general solution to obtain the final solution y(t) = 3/4 - 2/3e^(6t/7) + (3/7)sec(5t).
Learn more about Equation click here :brainly.com/question/649785
#SPJ11
Which best describes the range of the function f(x) = 2/3(6)^x after it has been reflected over the x-axis?
all real numbers
all real numbers less than 0
all real numbers greater than 0
all real numbers less than or equal to 0

Answers
Answer:
The answer is all real numbers less than or equal to 0
Solve this quadratic equation using the quadratic formula.x²-6x+6=0
A.x=3±√3
B.x=-6±√6
C.x=-3±√3
D.x=6±√6
Answers
a = 1
b = -6
c = 6
X = [-(-6) +/- square root (-6^2 -4(1)(6))] / 2(1)
= [6+/- square root (36-24)]/2
= [6+/- square root (12)] /2
= 3 +/- [(square root 12)/ 2]
= 3 +/- square root 3
Answer is A
find the area inside the larger loop and outside the smaller loop of the limacon r=\frac{1}{2} \cos(\theta).
Answers
The numerical values of the areas, we would need to evaluate these integrals. However, without a specific context or requirement for the area calculation, it is not possible to provide an exact numerical answer in this format.
To find the area inside the larger loop and outside the smaller loop of the limaçon with the polar equation r = (1/2)cos(θ), we need to determine the range of θ values that correspond to the loops.
The equation r = (1/2)cos(θ) describes a cardioid with a loop. The loop occurs when cos(θ) = 0, which happens when θ = π/2 and θ = 3π/2.
The larger loop is traced when θ ranges from 0 to π/2, while the smaller loop is traced when θ ranges from π/2 to 3π/2.
To calculate the areas, we integrate the formula for the area enclosed by a polar curve:
A = (1/2) ∫[θ1,θ2] r^2 dθ
For the larger loop, the area is:
A1 = (1/2) ∫[0,π/2] [(1/2)cos(θ)]^2 dθ
For the smaller loop, the area is:
A2 = (1/2) ∫[π/2,3π/2] [(1/2)cos(θ)]^2 dθ.
For such more questions on Numerical values:
https://brainly.com/question/27922641
#SPJ11
−14x −45=613 what is x?
Answers
Answer:x= -47
Step-by-step explanation:
-14x-45=613
-14x = 658
x = -47
Answer:
x= -47 i'm sure i did it right but tripple check it for me
Step-by-step explanation:
add 45 to both sides
divide both sides by -14
x= -47
The diameter of a circle is 8 cm. Find its circumference in terms of \piπ.
Answers
Here is your answer ^^
----------------------------------
C≈25.13cm
Explanation:
C=2πr
d=2r
Solving for C:
C=πd=π·8≈25.13274cm
-------------------------------------
Anyways bye! <3
If I decide to conduct a research to look for associations among variable, which of the following am I likely to find?
No associations
Some association
Either no association or some association
None of the above.
Answers
If you decide to conduct research to look for associations among variables, you are likely to find either no association or some association.
When conducting research to explore associations among variables, the outcome can vary. You may encounter situations where there is no significant association between the variables being studied. This means that the variables are independent of each other, and their values do not vary systematically or predictably in relation to one another.
On the other hand, you may also discover that there is some association between the variables. This indicates that there is a relationship or connection between the variables, and changes in one variable are related to changes in another variable.
It is important to note that the strength and nature of the associations can vary. Associations can be strong or weak, positive or negative, linear or nonlinear, depending on the specific research question and the variables under investigation.
When conducting research to explore associations among variables, it is likely that you will find either no association or some association. The specific outcome will depend on the nature of the variables and the analysis conducted. It is essential to interpret the results carefully and consider the context and limitations of the study when drawing conclusions about the associations observed.
Learn more about association ,visit:
https://brainly.com/question/30329420
#SPJ11
PLZ HELP
Solve the absolute value equation.
Check for extraneous solutions:The absolute value of (three x plus five) equals twelve x plus 8
Answers
Answer:
x = (13/9), -(3/9)
Step-by-step explanation:
|3x + 5| = 12x + 8
Since the equation is in absolutes we have
3x - 12x + 5 = 8
.: 5 - 9x = 8
-8 = 5 - 9x = 8
Remove 5 from both sides
-8 - 5 = -9x = 8 - 5
-13 = -9x = 3
x = (13/9), -(3/9)
The values of x for | 3x + 5 | = 12x + 8 is x = - 1/3 Or x = - 13/15.
What is an absolute value function?We know the absolute value function of the modulus function always outputs a positive value irrespective of the sign of the input.
In piecewise terms | x | = x for x ≥ 0 and | x | = - x for x < 0.
Given, | 3x + 5 | = 12x + 8.
So, (3x + 5) = 12x + 8 Or - (3x + 5) = 12x + 8.
3x + 5 = 12x + 8 Or -3x - 5 = 12x + 8.
- 9x = 3 Or - 15x = 13.
x = - 1/3 Or x = - 13/15.
learn more about absolute values here :
https://brainly.com/question/1301718
#SPJ2
I got it wiring but I don’t know what I did wrong

Answers
Answer:
because the answer is 6.601 not 6.501
Step-by-step explanation:
you must have done the work wrong
A project has the following projected outcomes in dollars: $240, $310, and $560. The probabilities of their outcomes are 20%, 60%, and 20% respectively. What is the expected value of these outcomes?
Answers
If the probabilities of their outcomes are 20%, 60%, and 20% respectively, the expected value of these outcomes is $346.
To calculate the expected value of the outcomes, we multiply each outcome by its corresponding probability and then sum up the results.
In this case, the projected outcomes are $240, $310, and $560, with probabilities of 20%, 60%, and 20% respectively.
To calculate the expected value, we use the formula:
Expected value = (Outcome 1 * Probability 1) + (Outcome 2 * Probability 2) + (Outcome 3 * Probability 3) + ...
Expected value = ($240 * 0.20) + ($310 * 0.60) + ($560 * 0.20)
Expected value = $48 + $186 + $112
Expected value = $346
The expected value represents the average value or the long-term average outcome we can expect from the given probabilities and outcomes. It provides a summary measure that helps in understanding the central tendency of the distribution of outcomes.
In this case, the expected value indicates that, on average, we can expect the project's outcome to be around $346.
To learn more about expected value click on,
https://brainly.com/question/31196935
#SPJ4
Bob's car cost $2.99 per pound. how much will 3.4 pounds cost?
Answers
Answer:
10.166
Step-by-step explanation:
2.99 x 3.4 = 10.166
Hope this helps, have a great day!
Michael started a savings account with $300. After 4 weeks, he had $350 dollars, and after 9 weeks, he had $400. What is the rate of
change of money in his savings account per week?
Person to answer get prize
Pls help

Answers
Answer:
$12.5
Step-by-step explanation:
all you do is divide the 4 weeks to the $50 he earns and get $12.5 every week.
simplify the following surd:-
1/4 √243 + √27/4
solve it with method
please hurry
Answers
Step-by-step explanation:
1/4 √243 + √27/4 =
(¼ √81×3) + (¼ √9×3) =
9/4 √3 + 3/4 √3 =
12/4 √3 =3√3
Which expression is equivalent to 2(a + 3)? (a + 2)3 3(a + 2), 6a + 2, or 2a + 6
Answers
Answer:
2a+6
I'm sure of it!!
trust me
The indicated function y(x) is a solution of the given differential equation. Use reduction of order or formula (5) in Section 4.2, e-SP(x) dx room/e Y2Y₁(x). dx (5) as instructed, to find a second solution y₂(x). (1-2x-x²)y" + 2(1+x)y - 2y = 0; Y₁ = x + 1 +3 Y₂=X- x 23/00
Answers
To find a second solution, y₂(x), of the given differential equation (1-2x-x²)y" + 2(1+x)y - 2y = 0, The equation is y₂(x) = (x + 1 + 3) ∫ [e^(-∫(2x + x² + C)dx)] / [(x + 1 + 3)^2] dx. Simplifying this expression gives us the second solution, y₂(x), for the given differential equation.
The given differential equation is a second-order linear homogeneous equation. We are given the first solution, y₁(x) = x + 1 + 3.
To find the second solution, y₂(x), we will use Formula (5) in Section 4.2, which states:
y₂(x) = y₁(x) ∫ [e^(-∫P(x)dx)] / [y₁(x)^2] dx
In this formula, P(x) represents the coefficient of the y' term in the differential equation.
First, we need to determine the value of P(x). From the given differential equation, we see that the coefficient of the y' term is 2(1+x).
Next, we calculate the integral of P(x):
∫ P(x) dx = ∫ 2(1+x) dx = 2x + x² + C
Now, we can substitute the values into Formula (5) to find y₂(x):
y₂(x) = (x + 1 + 3) ∫ [e^(-∫(2x + x² + C)dx)] / [(x + 1 + 3)^2] dx
Simplifying this expression gives us the second solution, y₂(x), for the given differential equation.
Note: The values for the constant of integration (C) and the limits of integration were not specified in the question, so they need to be determined based on the specific problem or initial conditions provided.
Learn more about differential equation here:
https://brainly.com/question/32524608
#SPJ11
The graph of f" is given in the figure below. (Click on the graph for a larger version.) Draw graphs of f and f', assuming both go through the origin, and use them to complete the following statements (enter the c-values as x1, x2, etc.): A. f(x) is greatest at x = ___________ B. f(x) is least at x = ___________ c. f'(x) is greatest at x = ___________ D. f'(x) is least at x = ___________ E. f"(x) is greatest at x = ___________ F. f"() is least at x = ___________
Answers
f(x) is greatest at x = x1, f(x) is least at x = x4, f'(x) is greatest at x = x3, f'(x) is least at x = x2, f''(x) is greatest at x = x2, and f''(x) is least at x = x3.
To draw the graph of f, we integrate f'' to obtain f', and then integrate f' to obtain f, assuming both functions go through the origin. The graph of f will be a cubic curve, with maximum and minimum points at x = x1 and x = x4, respectively.
To draw the graph of f', we find the slopes of the tangent lines to the graph of f at various points. The graph of f' will be a quadratic curve, with maximum and minimum points at x = x3 and x = x2, respectively.
Based on the graphs of f and f', we can determine the points where these functions are at their greatest and least. Specifically, f(x) is greatest at x = x1, and f(x) is least at x = x4. Similarly, f'(x) is greatest at x = x3, and f'(x) is least at x = x2.
Finally, we can also identify the points where f'' is at its greatest and least. The graph of f'' is a constant function, with value 2 between x = x2 and x = x3, and value 0 elsewhere. Therefore, f''(x) is greatest at x = x2, and f''(x) is least at x = x3.
To learn more about integrate click here, brainly.com/question/31744185
#SPJ11
T/F : If the first and second rows of an augmented matrix are (1,1,0) and (0,1,0) respectively, then the matrix is not in reduced row echelon form.
Answers
False.
the given augmented matrix is in reduced row echelon form.
The augmented matrix is said to be in reduced row echelon form (RREF) if it satisfies the following conditions:
1. The first nonzero element in each row (called the "pivot") is 1.
2. The pivot in each row is to the right of the pivot in the previous row.
3. All entries above and below each pivot are zero.
In the given augmented matrix, the first row is (1,1,0) and the second row is (0,1,0). Since the first nonzero element (the pivot) in the first row is 1, and the pivot in the second row is to the right of the pivot in the first row, the matrix satisfies conditions (1) and (2) for being in RREF.
Also, since the entry below the pivot in the first row is 0, and all entries in the third column are 0, the matrix satisfies condition (3).
Therefore, the given augmented matrix is in reduced row echelon form.
Visit to know more about Matrix:-
brainly.com/question/2456804
#SPJ11
use substitution to solve the system of equations. Write the solution as an ordered pair.
x + 2y = 14
y = 3x - 14
Answers
Answer:
Step-by-step explanation:
x + 2(3x - 14) = 14
x + 6x - 28 = 14
7x - 28 = 14
7x = 42
x = 6
y = 3(6) - 14
y = 18 - 14
y = 4
(6,4)
What percent of 4c is each expression?
*2a
Answers
4c is 50a/c % of the expression 2a
How to determine what percent of 4c is 2aFrom the question, we have the following parameters that can be used in our computation:
Expression = 2a
Percentage = 4c
Represent the percentage expression with x
So, we have the following equation
x% * Percentage = Expression
Substitute the known values in the above equation, so, we have the following representation
x% * 4c = 2a
Evaluate
x = 50a/c %
Express as percentage
Hence, the percentage is 50a/c %
Read more about percentage at
https://brainly.com/question/11360390
#SPJ1