Answers
From the first figure
Since LR and JV are 2 chords intersected at a point inside the circle, then
\(180-m\angle1=\frac{1}{2}\lbrack56+146\rbrack\)The angle next to <1 and form a line JV with it
\(\begin{gathered} 180-m\angle1=\frac{1}{2}\lbrack202\rbrack \\ 180-m\angle1=101 \end{gathered}\)Add m<1 to both sides and subtract 101 from both sides
\(\begin{gathered} 180-m\angle1+m\angle1-101=101-101+m\angle1 \\ 79^{\circ}=m\angle1 \end{gathered}\)In the second figure
Since TU is a tangent to the circle at point T
Since ST is a chord in the circle
Then angle of tangency subtended by the major arc ST, Its measure is half the measure of the subtended arc.
Since the major arc ST = the measure of the circle - the measure of the minor arc ST
\(m\angle2=\frac{1}{2}\lbrack360-arcST\rbrack\)Since the measure of the minor arc ST is 134 degrees, then
\(\begin{gathered} m\angle2=\frac{1}{2}\lbrack360-134\rbrack \\ m\angle2=\frac{1}{2}\lbrack226\rbrack \\ m\angle2=113^{\circ} \end{gathered}\)Related Questions
What's three digit number closest to 300 using 6, 2, 7, 3
Answers
Answer:
326
Step-by-step explanation:
Its hard to explain but you get the idea lol
Solve for the values of x for each of the following exponential equations and inequalities.
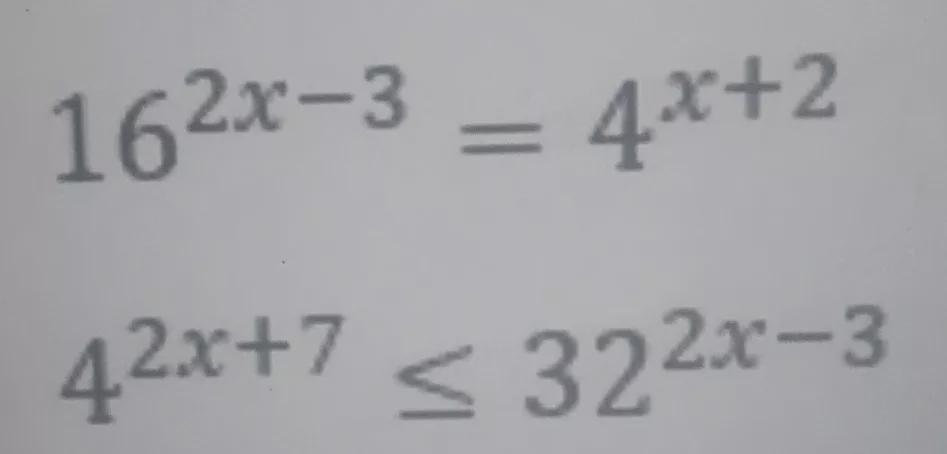
Answers
Given:
The exponential equation is,
a)
\(16^{2x-3}=4^{x+2}\)Solve the equation,
\(\begin{gathered} 16^{2x-3}=4^{x+2} \\ 4^{2(2x-3)}=4^{x+2} \\ \Rightarrow2(2x-3)=x+2 \\ 4x-6=x+2 \\ 4x-x=2+6 \\ 3x=8 \\ x=\frac{8}{3} \end{gathered}\)Answer: x = 8/3.
b) The inequality is,
\(4^{2x+7}\leq32^{2x-3}\)Solve the inequality,
\(\begin{gathered} 4^{2x+7}\leq32^{2x-3} \\ 2^{2(2x+7)}\leq2^{5(2x-3)} \\ \Rightarrow2(2x+7)\leq5(2x-3) \\ 4x+14\leq10x-15 \\ 14+15\leq10x-4x \\ 29\leq6x \\ \frac{29}{6}\leq x \\ x\ge\frac{29}{6} \end{gathered}\)Answer:
\(x\ge\frac{29}{6}\)
Use the given functions to find f (g(x)), and give the restrictions on x.
F(x)= 1/x-3 and g(x) = 3/x +3
F(g(x)) = ?
Where x(doesn’t = ?
Answers
Answer:
\(f(g(x)) = \frac{10x-9}{3 + 3x}\)
Step-by-step explanation:
Given
\(f(x) = \frac{1}{x} - 3\)
\(g(x) = \frac{3}{x} + 3\)
Required
Find f(g(x))
If: \(f(x) = \frac{1}{x} - 3\)
Then:
\(f(g(x)) = \frac{1}{3/x + 3} -3\)
Solve the denominator (take LCM)
\(f(g(x)) = \frac{1}{\frac{3+3x}{x}} -3\)
\(f(g(x)) = \frac{x}{3 + 3x} - 3\)
It can be solved further as:
\(f(g(x)) = \frac{x-3(3 + 3x)}{3 + 3x}\)
\(f(g(x)) = \frac{x-9 + 9x}{3 + 3x}\)
\(f(g(x)) = \frac{10x-9}{3 + 3x}\)
Here is a table of values for y= f(x).
x -2 -1 0 1 2 3 4 5 6
f(x) 5 6 7 8 9 10 11 12 13
Mark the statements that are true.
A. The domain for f(x) is the set {-2, -1, 0, 1, 2, 3, 4, 5, 6).
B. The range for f(x) is all real numbers.
C. f(-1) = 6
D. f(5) = -2
Answers
The statements that are true are:
A. The domain for f(x) is the set {-2, -1, 0, 1, 2, 3, 4, 5, 6).
C. f(-1) = 6
To determine the truth of each statement, we need to analyze the given table of values for the function f(x).
A. The domain for f(x) is the set {-2, -1, 0, 1, 2, 3, 4, 5, 6).
The x-values listed in the table are -2, -1, 0, 1, 2, 3, 4, 5, and 6. These are the inputs for the function, and therefore, they represent the domain of f(x). Thus, statement A is true.
B. The range for f(x) is all real numbers.
Looking at the y-values listed in the table for f(x), we can see that the range of f(x) is from 5 to 13. It does not include all real numbers, so statement B is false.
C. f(-1) = 6
From the table, we can see that when x = -1, f(x) = 6. Thus, statement C is true.
D. f(5) = -2
There is no entry in the table for f(5), so we cannot determine the value of f(5) from the given information. Therefore, statement D is false.
In conclusion, the true statements are A and C.
For more such questions on statements, click on:
https://brainly.com/question/27839142
#SPJ8
Jim vende perritos calientes a $2.95 cada uno y sándwiches de bistec a $9.95 cada uno en su carrito de comida. Durante un ajetreado festival al aire libre, vendió un total de 985 artículos por $7343,75. ¿Cuántos sándwiches de bistec vendió?
Answers
De acuerdo con la información, se puede inferir que Jim vendió 634 sándwiches de bistec y 351 perritos calientes.
¿Cómo identificar cuántos perros y sándwiches vendió Jim?Para identificar cuántos perros y sandwiches vendió Jim durante la feria debemos comprobar con diferentes números hasta encontrar el número correcto. En este caso, debemos multiplicar el valor de cada producto por un número específico e ir ajustado los valores hasta obtener el número total de productos.
En este caso, la cantidad de sándwiches vendidos por Jim sería 634 y perritos 351.
351 * 2.95 = 1,035.45634 * 9.95 = 6,308,36,308.3 + 1,035.45 = $7343,75Aprenda más sobre comidas en: https://brainly.com/question/7729754
#SPJ1
This problem refers to a right triangle ABC with C= 90°. Begin each problem by drawing a picture of the triangle with both the given and asked for information labeled appropriately. Answer to the nearest hundredth of a foot. If B=37.56 and a =49.94ft then b
Answers
The side b is approximately 80.02 feet in length. In a right triangle ABC with angle C equal to 90°, if angle B is 37.56° and side a is 49.94 feet, we can solve for side b using the trigonometric function sine.
First, we can label the triangle as follows:
Side a is opposite angle A,
Side b is opposite angle B,
Side c is the hypotenuse.
Let's label the triangle with the given and asked for information. Angle C is the right angle, angle B is 37.56°, side a is 49.94 feet, and side b is the side we are trying to find.
Using the sine function, we have:
sin(B) = opposite/hypotenuse
sin(37.56°) = a/b
Now we can substitute the known values:
sin(37.56°) = 49.94/b
To solve for b, we rearrange the equation:
b = 49.94 / sin(37.56°)
Using a calculator, we find:
b ≈ 80.02 feet.
For more such questions on Trigonometric function:
https://brainly.com/question/1143565
#SPJ8
HELP ME!!!!
ZEARN!!!!!!!!!

Answers
A common denominator is a shared multiple of the denominators of the fractions involved when adding or subtracting fractions. It enables fraction comparison and addition/subtraction.
Simplification is the process of reducing a fraction to its simplest form by dividing the numerator and denominator by their greatest common divisor. This is done to represent fractions in the simplest terms viable.
Conversion: The process of transferring a fraction from one form to another while retaining its equal value is known as conversion. Finding a common denominator or expressing a fraction in terms of a specified unit or fraction may be required.
Fraction Addition/Subtraction: When adding or subtracting fractions, a common denominator is required. This entails determining a common multiple of
To rewrite the expression 3 + 1/5 + 2/3 using fifteenths as the common denominator, we need to find a common denominator for 5 and 3, which is 15 (since 5 and 3 are both factors of 15).
First, let's convert the fractions 1/5 and 2/3 to fifteenths:
\((\frac{1}{5})(\frac{3}{3}) = \frac{3}{15}\)
\((\frac{2}{3})(\frac{5}{5}) = \frac{10}{15}\)
Now we can rewrite the expression using the common denominator:
\(3 + \frac{3}{15}+\frac{10}{15}\)
Which graph represents the piecewise-defined function? Y={6 if x ≤-3. 3 if-32
Answers
A piecewise function is a function that is defined by multiple sub-functions, each sub-function applying to a certain interval of the main function's domain (a sub-domain)
The three sub-functions are ;
y = 6
y = 3
y = 5
These three functions exist at a certain domain on the x-axis as shown.
From the graphs shown, the one that represents the piecewise function given is the first graph on the left.
It is shown below;

I need help figuring out how to solve these problems in the image below. Thank you in advance!

Answers
Answer:
Step -by-step explanation:
the angle of a triangle are in ration 1:3:5 then what is the sum of all find the messure of each angle
Answers
Answer:
1 : 3 : 5 = 20° : 60° : 100°
Step-by-step explanation:
Let the angle of the triangle be x
Given the following data;
1 : 3 : 5 = x : 3x : 5x
We know that the sum of the sides of a triangle is equal to 180 degrees.
x + 3x + 5x = 180
9x = 180
x = 180/9
x = 20°
Now, to find the measure of each angle.
For the first side;
x = 20°
For the second side;
3x = 3*20 = 60°
For the third side;
5x = 5*20 = 100°
calculate the following 2+2
Answers
Answer:4
Step-by-step explanation:
2+2 is 4
Which choices are equivalent to the fraction below? Check all that apply.

Answers
Find the vertex of the parabola. y = 3x2 – 30x + 77 a (-2,-5) b. (-5, -2) C. (5,2) d. (2,5) Please select the best answer from the choices provided Ο Α OB ОС D
Answers
Answer:
\(\text{C. }(5,2)\)
Step-by-step explanation:
The x-coordinate vertex of a parabola in standard form \(ax^2+bx+c\) is equal \(\frac{-b}{2a}\).
In \(y=3x^2-30x+77\), we have:
\(a\) equals 3\(b\) equals -30Therefore, the x-coordinate of the vertex is equal to \(\frac{-(-30)}{2(3)}=\frac{30}{6}=5\).
To find the y-coordinate, simply substitute \(x=5\) into the parabola's equation:
\(y=3x^2-30x+77,\\y=3(5^2)-30(5)+77,\\y=75-150+77,\\y=-75+77=2\)
Thus, the vertex of the parabola is \(\boxed{(5,2)}\)
Which expression is equivalent to 5(2+7)
A. 2(5+7)
B. 2+7(5)
C. 5(2)+7
D.5(2)+5(7)
Answers
Answer:
D
Step-by-step explanation:
So 5(2+7) equals 45
A. 2(5+7)=24
B. 2+7(5)=37
C. 5(2)+7=17
D.5(2)+5(7)=45
Only D equals 45
Hope I helped :D
What decimal is equivalent to 10/3?
Answers
Answer:
3.33333333 . . .
Step-by-step explanation:
Answer:
3.33333333
Step-by-step explanation:
Its a forever number, i forgot the term i think its called a terminal number, or nonterminal i forget. You divide 10 / 3 and get 3.33333333333333333333 forever
A bookshelf at a bookstore is 3 feet 9 inches wide. There are 18 copies of the same book on the shelf, which fit the shelf exactly. What is the width of 1 of the books?
Answers
Answer:
2.5 inches
Step-by-step explanation:
Given
Shelf Width = 3ft 9in
Copies = 18
Required
Determine the width of each book
This is calculated by dividing the shelf width by the number of copies.
Width = Shelf Width ÷ Copies
Width = (3 ft 9in) ÷ (18)
[Convert with to inches]
Width = (3 * 12 + 9) ÷ (18)
Width = (36 + 9) ÷ (18)
Width = 45 ÷ 18
Width = 2.5 inches
Hence, the width of each book is 2.5inches
The sector of a circle has an area of 104pi/9
square inches and a central angle with measure 65 degree
. What is the radius of the circle, in inches?
Answers
Answer:
Given:
Area of the sector (A) = 104π/9 square inches
Central angle (θ) = 65 degrees
The formula for the area of a sector of a circle is:
A = (θ/360) * π * r^2
We can rearrange this formula to solve for the radius (r):
r^2 = (A * 360) / (θ * π)
Plugging in the given values:
r^2 = (104π/9 * 360) / (65 * π)
r^2 = (104 * 40) / 9
r^2 = 4160 / 9
r^2 ≈ 462.22
Taking the square root of both sides:
r ≈ √462.22
r ≈ 21.49
Therefore, the radius of the circle is approximately 21.49 inches.
Answer: 8 inches
Step-by-step explanation:
Suppose Derrick is an insect enthusiast who measured the body length and weight of three insects in his backyard. His data are shown in the table.
Answers
Answer:
Step-by-step explanation:
What is the greatest number of acute angles that a triangle can contain?
A.3
B.1
C.0
D.2
Answers
Answer:
3
Step-by-step explanation:
We know that the sum of the angles of a triangle is 180
Assume that the angles are equal
x+x+x = 180
3x= 180
x = 180/3 =60
All three angles are less than 90 which makes them acute so we know that we can have 3 acute angles
Mr. Chen is buying cookies for the teachers and staff at Liberty Middle School. Each box contains 10 chocolate chip, 6 peanut butter, and 4 oatmeal raisin cookies. If there were 30 total peanut butter cookies, how many chocolate chip cookies did he buy? chocolate chip cookles
Answers
Answer:
50 chocolate chip cookies
Step-by-step explanation:
30÷6=5
if abcd is dilated by a factor of 1/2 the coordinate of d' would be

Answers
The co ordinate of the original coordinate of D is,
\(D(2,-2)\)So, the coordinate of the D' will get by multiplying the coordinate by 1/2
\(D^{\prime}(\frac{2}{2},-\frac{2}{2})=D^{\prime}(1,-1)\)So, the coordinate of D' is,
\(D^{\prime}(1,-1)\)evaluate (mn)(x) for x= -3
(mn)(-3) =
Answers
Answer:
-3mn
Step-by-step explanation:
Solve for h -110=13+3(4h-6)
Answers
Answer:
H= -35/4
Decimal form: -8.75
Explanation:
Subtract 13 from both sides. { -110 - 13 =3(4h - 6) }Simplify -110 -13 to -123 { -123 = 3 (4h - 6) }Divide both sides by 3 { -123/3 = 4h - 6 }simplify 123/3 to 41 { -41 = 4h - 6 }add 6 to both sides { -41 +6 = 4h }simplify -41 + 6 to -35 { -35 = 4h }divide both sides by 4 { - 35/4 = h }switch sides { h= - 35/4 }Customers generally find waiting in line to be an unpleasant experience. In addition to reducing the length of the wait itself, what other steps could a business take to reduce the frustration customers experience while waiting?
Answers
Answer:
OOP
Step-by-step explanation:
Complete the sIf k(x) = 5x – 6, which expression is equivalent to (k + k)(4)?teps to evaluate the following expression, given log3a = −0.631.
Answers
The expression that is equivalent to (k + k)(4) is 5(4) -6 +5(4) -6.
What are algebraic expressions?A combination of terms by operations like addition, subtraction, multiplication, and division, among others, form an algebraic expression (or variable expression). Let's look at the formula 5x + 7 as an example. We can therefore argue that 5x + 7 is an illustration of an algebraic statement.
Given that the function k(x) is:
k(x) = 5x -6
Substitute the value of x = 4:
k(4) = 5(4) -6
The value of:
(k + k)(4) = k(4) + k(4)
(k + k)(4) = 5(4) -6 +5(4) -6
Thus, the expression that is equivalent to (k + k)(4) is 5(4) -6 +5(4) -6.
Learn more about algebraic expression here:
https://brainly.com/question/953809
#SPJ1
help will mark Brainliest!!

Answers
Answer:
8/9n - 3
Step-by-step explanation:
Explanation:
When multiplying a fraction by a whole number, you multiply the numerator by the whole number. In this case, doing so would result in 8/9n. Because the same principle would apply for the other part of the equation, we can do 4/9 x -3 to get -12/9. -12/9 is improper, so we could standardize it to get the equation’s expression in simplified form. -12/9 simplified is -1 1/3. The answer would be 8/9n - 1 1/3 because when there is a negative factor, the expression becomes a subtraction problem. Thus, your equation is 8/9n - 1 1/3.
please help asap thank you

Answers
Answer:
10
Step-by-step explanation:
Step-by-step explanation:
the answer seems to be option c

Help its a two part question. Big points ans I will give brainliest

Answers
The equation of the axis of symmetry of the parabola is equal to x = 4.
How to derive the equation of the axis of symmetry
In this problem we find the representation of a parabola whose axis of symmetry is parallel with y-axis. The axis of symmetry passes through the vertex of the parabola. The definitions of the vertex and the axis of symmetry are, respectively:
Vertex
(x, y) = (h, k)
Axis of symmetry
x = h
If we know that h = - 4, then the equation of axis of symmetry is x = 4.
To learn more on parabolae: https://brainly.com/question/29267743
#SPJ1
If tan (x) = 24/19 (in Quadrant 1), find
Give exact answers.
sin (x/2) =
cos(x/2) =
tan (x/2) =
Answers
If x is in quadrant I, then both sin(x) and cos(x) are positive. The angle x/2 also belongs to quadrant I, and hence each of sin(x/2), cos(x/2), and tan(x/2) are positive.
Recall that for all x,
cos²(x) + sin²(x) = 1
and multiplying through both sides by 1/cos²(x) = sec²(x) gives another flavor of this identity,
1 + tan²(x) = sec²(x)
It follows that
sec(x) = √(1 + tan²(x)) = √937/19
which immediately gives us
cos(x) = 19/√937
and from the identity above we find
sin(x) = √(1 - cos²(x)) = 24/√937
Recall the half angle identity for cos :
cos²(x) = (1 + cos(2x))/2
which means
cos(x/2) = + √[(1 + cos(x))/2] = √[1/2 + 19/(2√937)]
Then
sin(x/2) = + √(1 - cos²(x/2)) = √[1/2 - 19/(2 √937)]
and by definition of tan,
tan(x/2) = sin(x/2) / cos(x/2) = 1/12 √[649/2 - 19 √937/2]
Just to be clear, the solutions are
\(\cos\left(\dfrac x2\right) = \sqrt{\dfrac12 + \dfrac{19}{2\sqrt{937}}}\)
\(\sin\left(\dfrac x2\right) = \sqrt{\dfrac12 - \dfrac{19}{2\sqrt{937}}}\)
\(\tan\left(\dfrac x2\right) = \dfrac1{12} \sqrt{\dfrac{649 - 19\sqrt{937}}2}\)
Evaluate the algebraic expression for the given values of x = 3 and y = 4. 8x - y
Answers
Answer: 24x-3
Step-by-step explanation:
This is because 8 x 3(x) = 24x - 3(y)
