Answers
Answer:
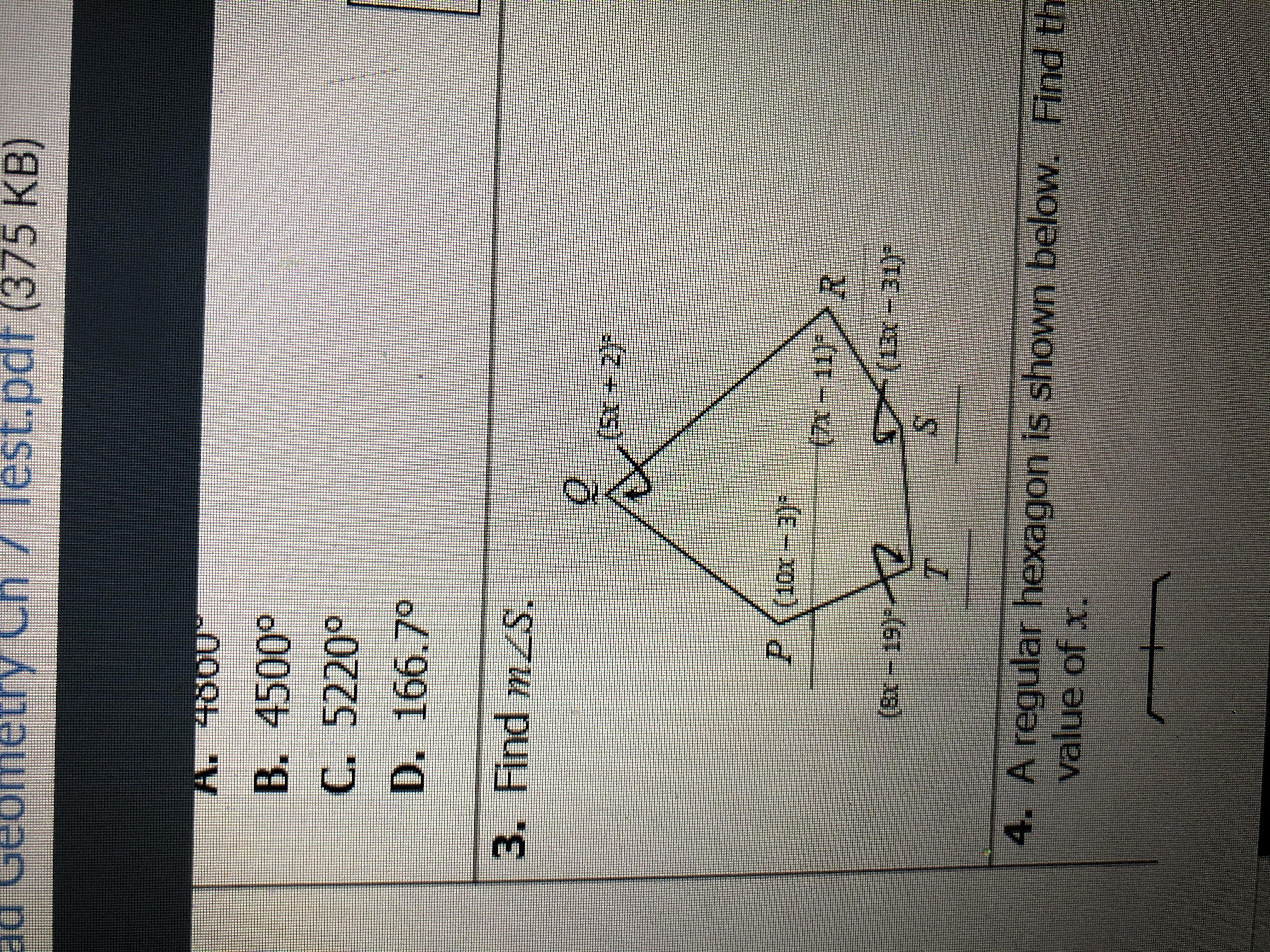
151°
Step-by-step explanation:
Pentagons interior angles are always 540°. So to solve, you must put
540= (5x+2)+(10x-3)+(8x-19)+(7x-11)+(13x-31). After solving this you will get x=14 and you can now substitute x in for measure s.
13(14) -31
182 - 31
measure of s = 151°
Answer: 151
Step-by-step explanation:
Step-by-step explanation:Pentagons interior angles are always 540°.
So to solve, you must put 540= (5x+2)+(10x-3)+(8x-19)+(7x-11)+(13x-31).
After solving this you will get x=14 and you can now substitute x in for measure s.
13(14) -31182 - 31
measure of s = 151°
Related Questions
Write the number for twenty-one million six hundred thousand
Answers
Find the missing side lengths. Answers are in simplest radical form with the denominator rationalized.

Answers
Answer:
7 sq rt 2
Step-by-step explanation:
must use pythagorean theorem: square of each leg = square of hypotenuse
7 squared the 7 squared = u squared
49+49=u squared
u = square root of 98, which is sq root of 49 times sq root of 2
The Pear company sells pPhones. The cost to manufacture a pPhones is
C(x) = -21x² + 45000z+21159 dollars (this includes overhead costs and production costs for each
pPhone). If the company sells ™ pPhones for the maximum price they can fetch, the revenue function will
be R(x) = -30x² + 189000 dollars.
How many pPhones should the Pear company produce and sell to maximimze profit? (Remember that
profit-revenue-cost.)
X=
Answers
Step-by-step explanation:
To maximize profit, the Pear company needs to find the value of x that maximizes the difference between revenue and cost, which is the profit function P(x) = R(x) - C(x).
P(x) = R(x) - C(x)
P(x) = (-30x² + 189000) - (-21x² + 45000x + 21159)
P(x) = -9x² + 45000x + 157841
To find the value of x that maximizes P(x), we can use the formula x = -b/2a, where a = -9 and b = 45000.
x = -b/2a
x = -45000/(2*(-9))
x = 2500
So, the Pear company should produce and sell 2500 pPhones to maximize profit
To find the number of Phones that the Pear company should produce and sell to maximize profit, we need to use the profit function, which is:
P(x) = R(x) - C(x)
where R(x) is the revenue function and C(x) is the cost function.
Substituting the given functions, we get:
P(x) = (-30x² + 189000) - (-21x² + 45000x + 21159)
P(x) = -9x² + 104000x - 21159
To maximize profit, we need to find the value of x that maximizes P(x). To do this, we can take the derivative of P(x) with respect to x and set it equal to zero:
P'(x) = -18x + 104000 = 0
x = 5777.78
Since we can't produce a fractional number of Phones, we should round this down to 5777 Phones.
Therefore, the Pear company should produce and sell 5777 Phones to maximize profit.
Solve the equation: x²-2x=8
Show all the Steps with explanation.
Answers
Answer:
x = 4, -2
Step-by-step explanation:
x^2-2x=8
Move the constant term to the right side of the equation.
x^2 - 2x = 8
Take half of the coefficient of x and square it.
(-2/2)^2 = 1
Add the square to both sides of the equation.
x^2 - 2x + 1 = 8 + 1
Factor the perfect square trinomial.
(x - 1)^2 = 9
Take the square root of both sides of the equation.
x-1=\(\sqrt{9}\)
x-1=±3
Isolate x to find the solutions.
Taking positive
x=3+1=4
x=4
Taking negative
x=-3+1
x=-2
The solutions are:
x = 4, -2
Answer:
\(x = -2,\;\;x=4\)
Step-by-step explanation:
To solve the quadratic equation x² - 2x = 8 by factoring, subtract 8 from both sides of the equation so that it is in the form ax² + bx + c = 0:
\(x^2-2x-8=8-8\)
\(x^2-2x-8=0\)
Find two numbers whose product is equal to the product of the coefficient of the x²-term and the constant term, and whose sum is equal to the coefficient of the x-term.
The two numbers whose product is -8 and sum is -2 are -4 and 2.
Rewrite the coefficient of the middle term as the sum of these two numbers:
\(x^2-4x+2x-8=0\)
Factor the first two terms and the last two terms separately:
\(x(x-4)+2(x-4)=0\)
Factor out the common term (x - 4):
\((x+2)(x-4)=0\)
Apply the zero-product property:
\(x+2=0 \implies x=-2\)
\(x-4=0 \implies x=4\)
Therefore, the solutions to the given quadratic equation are:
\(\boxed{x = -2,\;\;x=4}\)
Given the function fx) = 5x² - 9x + 18, find f (3).
A)
f(3) = 31
B)
| (5) = 36
(3) = 49
D)
(3) - 85
Answers
Answer:
f(36)
Step-by-step explanation:
f(3)=5(3)²-9(3)+18
f(3)=5(9)-27+18
f(3)=45-27+18
f(3)=36
3/4 ∙( 15/4 −3 1/2 )÷1 1/3
Answers
Answer:
9/64
Step-by-step explanation:
\(=0.75\times \frac{\left(3.75+-3.5\right)}{1.3}\\0.75\times \frac{\left(3.75+-3.5\right)}{1.3}\\=0.75\times \frac{0.25}{1.3}\\=0.75\times 0.1875(\left a.k.a\:\frac{3}{16}\right)\\\frac{\left(3\times 0.1875\right)}{4}\\\mathrm{\left(Clarification:\:The\:\:math\:\:above\:\:is\:\:a\:\:broken\:\:down\:version\:of\:the\:original\:problem.\right)}\\=\frac{0.5625\left(\frac{9}{16}\right) }{4}\\=0.1406\left(\frac{9}{64}\right)\)
Hope this helps!
What is the tan (X) in triangle XYZ? /35 3528 2821 21

Answers
Tan x = opposite side / adjacent side
opposite side: 21
Adjacent side: 28
Replacing:
Tan x = 21/28
Find the measures of the angles.
(8x-1)º
(3x + 4)º
(3x + 9)
°
95, 40, 45
90, 25, 65
80, 52, 48
70, 68, 42
Answers
Answer:
answer is - 95, 40, 45
Step-by-step explanation:
Since the interior angles of a triangle add up to be 180 degrees, I set up the equation like so:
(8x-1)+(3x + 4)+(3x + 9) = 180
=> 14x +12 = 180
=> 14x = 180-12
=> x = 168/14 = 12
now putting value of x = 12
we get---
8*12 -1 = 96-1 = 95
3*12 + 4 = 36+4 = 40
3*12 + 9 = 36 + 9 = 45
( Answer )
On a coordinate plane, 2 parallelograms are shown. Parallelogram 1 has points (0, 2), (2, 6), (6, 4), and (4, 0). Parallelogram 2 has points (2, 0), (4, negative 6), (2, negative 8), and (0, negative 2). How do the areas of the parallelograms compare? The area of parallelogram 1 is 4 square units greater than the area of parallelogram 2. The area of parallelogram 1 is 2 square units greater than the area of parallelogram 2. The area of parallelogram 1 is equal to the area of parallelogram 2. The area of parallelogram 1 is 2 square units less than the area of parallelogram 2.
Answers
The areas of the parallelograms compare by option : A. The area of parallelograms 1 is 4 square units greater than the area of parallelogram 2.
What is the parallelograms about?Note that the part that is filled by a flat form or the surface of an item is called the area.
Note that:
A₁ = the area of parallelogram 1
A₁ = the area of parallelogram 2
l₁ = the distance between the points that is (2,6),(0,2)
l₂ = the distance between the points that is (4,0)(0,2)
b₁ = the distance between the points that is (2,0),(0,-2)
b₂ = the distance between the points that is (2,6),(4,-6)
So
A₁ = l₁ × b₁
=4.47 ×4.47
19.89 sq. unit
A₂= l₂×b₂
2.82 × 6.342
17.88 sq. unit
A₁-A₂ = 19.89 sq. unit - 17.88 sq. unit'
= 2.01
Therefore, The areas of the parallelograms compare by option : A. The area of parallelograms 1 is 4 square units greater than the area of parallelogram 2.
Learn more about parallelograms from
https://brainly.com/question/23774966
#SPJ1
PRECALCULUS HELP IM BEGGING YOU
Dean has built a ferris wheel in his backyard. It has a diameter of 10 feet and completes 30 revolutions per minute. Sketch a quick graph and find the period of the function that describes the height above the ground of a seat on the outside edge of this ferris wheel.
Answers
Answer: Period = 2 seconds
Graph is shown below
========================================================
Explanation:
1 minute = 60 seconds
We have 30 revolutions every 60 seconds, so we can write the ratio
30 rev: 60 sec
Divide both parts by 30 to turn that "30 rev" into "1 rev"
30 rev: 60 sec
30/30 rev: 60/30 sec
1 rev : 2 sec
This tells us that each full revolution takes 2 seconds. This is the period of the ferris wheel. The period is the length of each cycle.
The cyclic or periodic nature of this motion heavily implies we'll be dealing with a sine or cosine function of some kind. Let's go with sine.
Side note: cosine is really a sine function in disguise (it's just a phase shifted version of it).
---------------------
The general sine curve equation is
y = A*sin(B(x-C)) + D
where
|A| = amplitudeB = 2pi/T with T being the periodC handles phase shifts (left and right shifting)D handles vertical shifting, and y = D is the equation of the midline---------------------
The wheel is 10 feet in diameter, so 10/2 = 5 is the radius. This is also the amplitude because it is the distance from the midline to either the highest point (10 ft) or lowest point (0 ft). So A = 5.
Since T = 2 is the period, this means,
B = 2pi/T
B = 2pi/2
B = pi
We don't have any phase shifts to worry about so C = 0.
The midline is D = 5 since this is halfway up
----------------------
Putting all the pieces together, we get this sine equation
y = A*sin(B(x-C)) + D
y = 5*sin(pi*(x-0)) + 5
y = 5*sin(pi*x) + 5
The graph is shown below.
x = time in seconds, y = height of the seat

When the sum of a number and 3 is subtracted from 10 the result is 5. What is the integer
Answers
Please help will give brainlyist

Answers
Since the auditorium can hold 600 and the student body will be divide by four parts
The answer is
x ≤ 2400
FIND Y
PLEASE HELP ILL GIVE BRAINLIESTTTT :))

Answers
Answer:
y = 22
Step-by-step explanation:
The sum of the 3 angles in a triangle = 180°
Sum the angles in the lower triangle and equate to 180°
∠ 1 + 19° + 41° = 180°
∠ 1 + 60° = 180° ( subtract 60° from both sides )
∠ 1 = 120°
∠ 1 and ∠ 2 are vertically opposite angles and are congruent , so
∠ 2 = 120°
Sum the angles in the upper triangle and equate to 180
y + 120 + 38 = 180
y + 158 = 180 ( subtract 158 from both sides )
y = 22
A telescope contains both a parabolic mirror and a hyperbolic mirror. They share focus , which is 46feet above the vertex of the parabola. The hyperbola's second focus is 6 ft above the parabola's vertex. The vertex of the hyperbolic mirror is 3 ft below . Find the equation of the hyperbola if the center is at the origin of a coordinate system and the foci are on the y-axis. Complete the equation.
Answers
the center is at the origin of a coordinate system and the foci are on the y-axis, then the foci are symmetric about the origin.
The hyperbola focus F1 is 46 feet above the vertex of the parabola and the hyperbola focus F2 is 6 ft above the parabola's vertex. Then the distance F1F2 is 46-6=40 ft.
In terms of hyperbola, F1F2=2c, c=20.
The vertex of the hyperba is 2 ft below focus F1, then in terms of hyperbola c-a=2 and a=c-2=18 ft.
Use formula c^2=a^2+b^2c
2
=a
2
+b
2
to find b:
\begin{gathered} (20)^2=(18)^2+b^2,\\ b^2=400-324=76 \end{gathered}
(20)
2
=(18)
2
+b
2
,
b
2
=400−324=76
.
The branches of hyperbola go in y-direction, so the equation of hyperbola is
\dfrac{y^2}{b^2}- \dfrac{x^2}{a^2}=1
b
2
y
2
−
a
2
x
2
=1 .
Substitute a and b:
\dfrac{y^2}{76}- \dfrac{x^2}{324}=1
76
y
2
−
324
x
2
=1 .
Escribir la ecuación de la circunferencia de centro (3,4) y radio r = 2
Answers
Find the distance between the points.
(−3,− 8), (6, – 8)
The distance is
Answers
To calculate the distance between two points:
We apply the following formula:
d = √(x₂ - x₁)² + (y₂ - y₁)²
The points are:
(x₁,y₁) = -3, -8(x₂,y₂) = 6, -8We substitute data and solve:
\(\bf{d=\sqrt{(6-(-3))^2+(-8-8(-8))^2 } }\\ \\ \bf{ d=\sqrt{9^2+0^2}=\sqrt{81+0} }\\ \\ \bf{d=\sqrt{81}=9 }\)
The distance between the points (−3,− 8), (6, – 8) is 9.
solve the system of equations by using substitution
y=2x-2
2x+y=10
Answers
2x+2x-2=10
4x-2=10
+2 +2
4x=8
x=2
y=2(2)-2
Y=2
An automobile manufacturer has given its jeep a 51.3 miles/gallon (MPG) rating. An independent testing firm has been contracted to test the actual MPG for this jeep since it is believed that the jeep has an incorrect manufacturer's MPG rating. After testing 230 jeeps, they found a mean MPG of 51.1. Assume the population variance is known to be 6.25. A level of significance of 0.02 will be used. Make the decision to reject or fail to reject the null hypothesis.
Answers
Answer:
The p-value of the test is 0.2262 > 0.02, which means that the decision is to fail to reject the null hypothesis.
Step-by-step explanation:
An automobile manufacturer has given its jeep a 51.3 miles/gallon (MPG) rating.
At the null hypothesis, we test if the mean is of 51.3, that is:
\(H_0: \mu = 51.3\)
An independent testing firm has been contracted to test the actual MPG for this jeep since it is believed that the jeep has an incorrect manufacturer's MPG rating.
This means that at the alternative hypothesis, we test if the mean is different of 51.3, that is:
\(H_0: \mu \neq 51.3\)
The test statistic is:
\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis, \(\sigma\) is the standard deviation and n is the size of the sample.
51.3 is tested at the null hypothesis:
This means that \(\mu = 51.3\)
After testing 230 jeeps, they found a mean MPG of 51.1. Assume the population variance is known to be 6.25.
This means that \(n = 230, X = 51.1, \sigma = \sqrt{6.25} = 2.5\)
Value of the test statistic:
\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
\(z = \frac{51.1 - 51.3}{\frac{2.5}{\sqrt{230}}}\)
\(z = -1.21\)
P-value of the test and decision:
The p-value of the test is the probability of the sample mean differing from 51.1 by at least 0.2, which is P(|z| > 1.21), which is 2 multiplied by the p-value of z = -1.21.
Looking at the z-table, z = -1.21 has a p-value of 0.1131.
2*0.1131 = 0.2262
The p-value of the test is 0.2262 > 0.02, which means that the decision is to fail to reject the null hypothesis.
25-40x = x - 10
solve this radical equation
the 25-40x is supposed to be in a square root

Answers
What is the greatest common factor (GFC) for 18 and 66
Answers
Answer:
The answer is 6!!
Step-by-step explanation: Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66
After listing all of the factors, simply find the number that is shown in both of their factors but find the greatest number.
For example 3 is a factor that is the same but isn't the highest factor that is shown in both, it is 6! Hope this helps and Happy Halloween!!! :D
Are x = -4 and x = 6 solutions to 5x + 7 < 22?
TRUE OR FALSE
Answers
Answer:
false
Step-by-step explanation:
only x=-4 would work in the inequality
A window is to be built in the shape of a rectangle surmounted by an isosceles triangle. The area of the window must be 6 square meters. Use Lagrange Multipliers to find the width and height of the rectangle for which the perimeter of the window will be as small as possible
Answers
Answer:
x = 2.536 m
y = 2 m
Step-by-step explanation:
Considering the three sides of the rectangle and the isosceles triangle
when resolving the width and height of the rectangle to achieve the smallest possible perimeter.
step 1 :
Area of window = xy + 1/2 xz , perimeter = x + 2y + 2c
c = \(\sqrt{z^2 + 1/4 x^2 }\)
we are tasked with minimizing the perimeter ( p ) subject to A = 6
attached below is the detailed solution of the given problem

The midpoint of AB is M(-4,2). If the coordinates of A are (-7,3), what are the
coordinates of B?
Answers
The midpoint of AB is M(-4,2). If the coordinates of A are (-7,3), and the coordinates of B is (-1, 1).
To find the coordinates of point B, we can use the midpoint formula, which states that the coordinates of the midpoint between two points (A and B) can be found by averaging the corresponding coordinates.
Let's denote the coordinates of point A as (x1, y1) and the coordinates of point B as (x2, y2). The midpoint M is given as (-4, 2).
Using the midpoint formula, we can set up the following equations:
(x1 + x2) / 2 = -4
(y1 + y2) / 2 = 2
Substituting the coordinates of point A (-7, 3), we have:
(-7 + x2) / 2 = -4
(3 + y2) / 2 = 2
Simplifying the equations:
-7 + x2 = -8
3 + y2 = 4
Solving for x2 and y2:
x2 = -8 + 7 = -1
y2 = 4 - 3 = 1
Therefore, the coordinates of point B are (-1, 1).
Know more about coordinates here:
https://brainly.com/question/29765572
#SPJ8
What is the domain of the following function?

Answers
The domain of the function or relation is {6, 9, -4 and 2}
How to determine the domain of the function?The function is represented by the set of relation or ordered pairs
The ordered pairs in the relation are:
(x, y) = (6, -3), (9, -3), (-4, 1) and (2, 1)
Remove the y values in the above domain
x = 6, 9, -4 and 2
The x values represent the domain of the function
Hence, the domain of the function or relation is {6, 9, -4 and 2}
Read more about domain at:
https://brainly.com/question/1770447
#SPJ1
Write an inequality that represents the statement “x is at most –5 or at least 7.”
Answers
Answer:
x ≤ - 5 or x ≥ 7
or, in interval notation
[ - ∞, -5] ∪ [7, ∞]
Step-by-step explanation:
From the question we get the following two inequalities
x is at most -5 ==> x ≤ -5
x is at least 7 ==> x ≥ 7 which can be rewritten as 7 ≤ x
This can be written as
x ≤ - 5 or x ≥ 7
In interval notation this would be
[ - ∞, -5] ∪ [7, ∞]
On the number line this would be represented as shown in the figure

In certain deep parts of oceans, the pressure of sea water,P, in pounds per square foot, at a depth of d feet below the surface, is given by the following equation P=14+ 4d/9
If a scientific team uses special equipment to measure the pressure under water and find it to be 306 pounds per square foot, at what depth is the team making their measurements?
Answers
It is important to note that this equation assumes a constant density of seawater, which is not always the case in the deep ocean. In addition, the pressure at a given depth can vary depending on factors such as temperature and salinity. This equation should be used with caution and in conjunction with other measurements and data analysis techniques.
The given equation for pressure in pounds per square foot at a depth of d feet is P = 14 + 4d/9. We are given that the pressure measured by the scientific team is 306 pounds per square foot. To find the depth at which this pressure is measured, we need to solve the equation for d.
Substituting P = 306 in the equation, we get:
306 = 14 + 4d/9
Multiplying both sides by 9, we get:
2754 = 126 + 4d
Subtracting 126 from both sides, we get:
2628 = 4d
Dividing both sides by 4, we get:
d = 657 feet
The scientific team is measuring the pressure at a depth of 657 feet below the surface of the ocean.
For such more questions on Measurements:
https://brainly.com/question/27122947
#SPJ11
Please solve assignments due today

Answers
1. Initial prediction for the data set with smaller Mean Absolute Deviation was Period A. Prediction was wrong.
2. The Mean Absolute Deviation for Period A is 1.8 and Period B, 1.1
This means that period B has a smaller Mean absolute deviation.
How do we calculate the Mean Absolute Deviation?We start by finding the mean for each set;
Period A: Mean = (1×92 + 1×94 + 3×95 + 1×96 + 2×97 + 1×99 + 1×100)/10
= 960/10
= 96
Period B: Mean = (1×94 + 3×95 + 1×96 + 4×97 + 1×98)/10
= 961/10
= 96.1
Period A:
Mean Absolute Deviation = ((92-96) + (94-96) + 3(95-96) + (96-96) + 2(97-96) + (99-96) + (100-96))/10
Mean Absolute Deviation = (4 + 2 + 3 + 0 + 2 + 3 + 4)/10
Mean Absolute Deviation = 1.8
Period B:
Mean Absolute Deviation = ((94-96.1) + 3(95-96.1) + (96-96.1) + 4(97-96.1) + (98-96.1))/10
Mean Absolute Deviation = (2.1 + 3.3 + 0.1 + 3.6 + 1.9)/10
Mean Absolute Deviation = 1.1
Find more exercises on Mean Absolute Deviation;
https://brainly.com/question/10528201
#SPJ1
Express this number in scientific notation. 0.3643
Answers
Answer:
3.643 × 10-1
Step-by-step explanation:
What are the zeros of the function

Answers
Answer:
(1,0)
Step-by-step explanation:
A.K.A the y and x intercepts you might need to do a little more math you get the y intercept tho
What is the square root of -1
Answers
Answer:
The square root of ( -1 ) is i
Answer:
the square root of -1 is i
Have a nice day! :D
Step-by-step explanation: