Find the indicated term of each binomial expansion.
second term of (2 g+2 h)⁷
Answers
The second term of the binomial expansion of (2g + 2h)⁷ is 896g⁶h.
To find the second term of the binomial expansion of (2g + 2h)⁷, we can use the binomial theorem.
The binomial theorem states that the expansion of (a + b)ⁿ can be written as:
(a + b)ⁿ = C(n, 0) * aⁿ * b⁰ + C(n, 1) * aⁿ⁻¹ * b¹ + C(n, 2) * aⁿ⁻² * b² + ... + C(n, n-1) * a¹ * bⁿ⁻¹ + C(n, n) * a⁰ * bⁿ
where C(n, k) represents the binomial coefficient, given by C(n, k) = n! / (k! * (n - k)!).
In this case, we have (2g + 2h)⁷. Using the binomial theorem, the second term will correspond to the coefficient C(7, 1) multiplied by (2g)⁶ multiplied by (2h)¹.
Let's calculate it-
C(7, 1) = 7! / (1! * (7 - 1)!) = 7! / (1! * 6!) = 7
(2g)⁶ = (2)⁶ * g⁶ = 64g⁶
(2h)¹ = (2)¹ * h¹ = 2h
Now, we multiply the coefficient, (2g)⁶, and (2h)¹:
Second term = C(7, 1) * (2g)⁶ * (2h)¹ = 7 * 64g⁶ * 2h = 896g⁶h
Therefore, the second term of the binomial expansion of (2g + 2h)⁷ is 896g⁶h.
Learn more about binomial theorem here:
https://brainly.com/question/29254990
#SPJ11
Related Questions
match the correct base shape to each prism. some cards may be used more than once.


Answers
Looking at figure A, we have a prism with a triangular base that looks like a right triangle.
Since the prism has a right triangular base, the base shape is a right triangle (shape 5).
Looking at figure B, we have a prism with a pentagonal base.
Since the prism has a pentagonal base, the base shape is a pentagon (shape 1).
Looking at figure C, we have a prism with a triangular base that looks like an equilateral triangle.
Since the prism has an equilateral triangle base, the base shape is an equilateral triangle.(shape 4).
Looking at figure D, we have a prism with a triangular base that looks like an equilateral triangle.
Since the prism has an equilateral triangle base, the base shape is an equilateral triangle.(shape 4).
The vertices of a triangle are as follows:
(4, 4), (6, 10), and (8, 0)
If you dilate the triangle by a scale factor of 1/2, what are the vertices of the new triangle?
Answers
Answer:
(2, 2), (3, 5), and (4, 0)
Step-by-step explanation:
Dilating, assuming you start at origin, means to just multiply by scale factor.
what is the purpose of using prefixes in the metric system
Answers
The purpose of using prefix in the metric system is to properly sale the basis of the unit so large numeric values can be used effectively.
If the metric system is not properly prefixed it can lead to various inconsistencies in the the numeric values. for example if you go to a computer store and you do not know the scale like (kb, mb, gb, tb) you will get quite confused about what is the sales representative saying
Consider you went to a store to get sugar and you do not know the metric system say(gram, kg, mg) you would not know how much sugar you need directly by taking it in your hands.
To know more about metric system one may refer to
https://brainly.com/question/25966695
#SPJ4
Find the value of x for which m|| n is ?

Answers
-3x -3x
x-23 =19
+23 +23
x= 42
A company uses samples of size 9 to construct an X-bar chart to control the mean of the diameter of a drive shaft. On a certain day, a new employee takes a sample of size 4 and plot this sample average on the X-bar chart that is constructed with samples of size 9. Assuming the process is in control, what is the probability that this sample average falls outside the 3- sigma control limits of the X-bar chart?
Group of answer choices
0.00%
0.27%
1.24%
4.55%
13.36%
18.35%
31.73%
Answers
The probability that the sample average falls outside the 3-sigma control limits of the X-bar chart is 0.27%.
The 3-sigma control limits are calculated using the standard deviation of the process. If the process is in control, then 99.73% of the sample averages will fall within the 3-sigma control limits. The remaining 0.27% of the sample averages will fall outside the control limits.
In this case, the sample size is 4, which is smaller than the sample size of 9 that was used to construct the control chart. This means that the control limits for the sample of size 4 will be narrower than the control limits for the sample of size 9.
As a result, the probability that the sample average falls outside the control limits will be higher for the sample of size 4.
Specifically, the probability that the sample average falls outside the 3-sigma control limits for a sample of size 4 is 0.27%. This means that there is a 0.27% chance that the new employee will observe a sample average that falls outside the control limits, even if the process is in control.
Visit here to learn more about probability:
brainly.com/question/13604758
#SPJ11
A child's height is measured and compared to his peers. Explain what it means if the child's height has a z-score of -1.5 Choose the best answer. a. The child is shorter than what the model predicted for his height. b. The child's height is 1.5 standard deviations below the mean height for children his age. The child's height is -1.5 standard deviations below the mean height for children his age. d. The child's height is unusually low for children his age. e. The child's height is 1.5 inches below average when compared to the height of his peers.
Answers
The correct answer is b.
The child's height is 1.5 standard deviations below the mean height for children his age.
A z-score is a measure of how many standard deviations an observation is away from the mean of the distribution. A z-score of -1.5 means that the child's height is 1.5 standard deviations below the mean height for children his age. This indicates that the child's height is lower than the average height of his peers.
Option a is incorrect because the z-score does not measure what the model predicted for the child's height, but rather how far the child's height deviates from the mean height of his peers.
Option c is incorrect because the z-score does not measure how low or high the child's height is in absolute terms, but rather how far it deviates from the mean.
Option d is partially correct but not specific enough, as the z-score tells us how much lower the child's height is compared to the mean, but not whether it is unusually low or not.
Option e is incorrect because the z-score is a measure of standard deviations, not inches.
To know more about standard deviations refer here
https://brainly.com/question/29115611#
#SPJ11
If a child's height has a z-score of -1.5, it means that the child's height is 1.5 standard deviations below the mean height for children his age. So the correct option is C.
The z-score measures the number of standard deviations a particular data point is from the mean of the distribution. A z-score of -1.5 indicates that the child's height is 1.5 standard deviations below the mean height for children his age. Since the z-score is negative, it means that the child's height is below the mean height for his age group. In other words, the child is shorter than what the model predicted for his height.
The mean height for children his age represents the average height of all children in that age group. Standard deviation measures the amount of variability in the height measurements of the children in that age group. A z-score of -1.5 indicates that the child's height is 1.5 standard deviations below the mean height for his age group. This means that the child's height is significantly lower than that of his peers.
Therefore, if a child's height has a z-score of -1.5, it means that the child's height is significantly lower than the mean height for children his age, and he is shorter than what the model predicted for his height.
To learn more about standard deviations here:
brainly.com/question/13498201#
#SPJ11
x − 2y = −3
y = −2x − 1
(1, 1)
(1, −1)
(−1, 1)
(−1, −1)
Answers
The solution is (-1, 1). The solution has been obtained using linear equations.
What is a linear equation?
The linear equation with the highest degree of one is this one. This implies that there are no variables in a linear equation with exponent greater than 1. This equation results in the graph having a straight line.
In order to obtain the solution, we will see which point satisfies both the equations.
1. (1,1)
⇒x-2y = -3
⇒1-2 = -3
⇒-1 ≠ -3
So, this is not the solution.
2. (1, -1)
⇒x-2y = -3
⇒1-2(-1) = -3
⇒1+2 = -3
⇒3 ≠ -3
So, this is not the solution.
3. (-1, 1)
⇒x-2y = -3
⇒-1-2 = -3
⇒-3 = -3
Second equation
⇒y = -2x - 1
⇒1 = -2(-1) - 1
⇒1 = 2 - 1
⇒1 = 1
Thus, this is the solution.
Hence, the solution is (-1, 1).
Learn more about linear equation from the given link
https://brainly.com/question/30092358
#SPJ1
Find the measure of angle BDE. ML ABC=155
and muc=60.
155
C
B
bo
x
E

Answers
Answer:
∠ BDE = 85°
Step-by-step explanation:
The exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
∠ ABC is an exterior angle of the triangle, then
∠ C + ∠ BDC = 155
60 + ∠ BDC = 155 ( subtract 60 from both sides )
∠ BDC = 95°
∠ BDE and ∠ BDC are adjacent angles and are supplementary, thus
∠ BDE = 180° - 95° = 85°
What is the probability that a randomly chosen college student exercises in the morning or afternoon? 0. 37 0. 39 0. 62 0. 76.
Answers
The probability that a randomly chosen college student exercises in the morning or afternoon is 0.76
We have given that the M be the event that the student exercises in the morning and A be the event that the student exercises in the afternoon.
To find : The probability that a randomly chosen college student exercises in the morning or afternoon
P(M) = 0.25+0.37 = 0.62
P(A) = 0.14+0.37 = 0.51
P(M and A) = 0.37
Now,
P(M or A) = P(M) + P(A) - P(M and A)
= 0.62 + 0.51 - 0.37
= 0.76
Hence, Option last 0.76 is the correct choice.
To learn more about the probability click here:
brainly.com/question/30034780
#SPJ4
Literally struggle help pls (right answer only ) giving brainliest
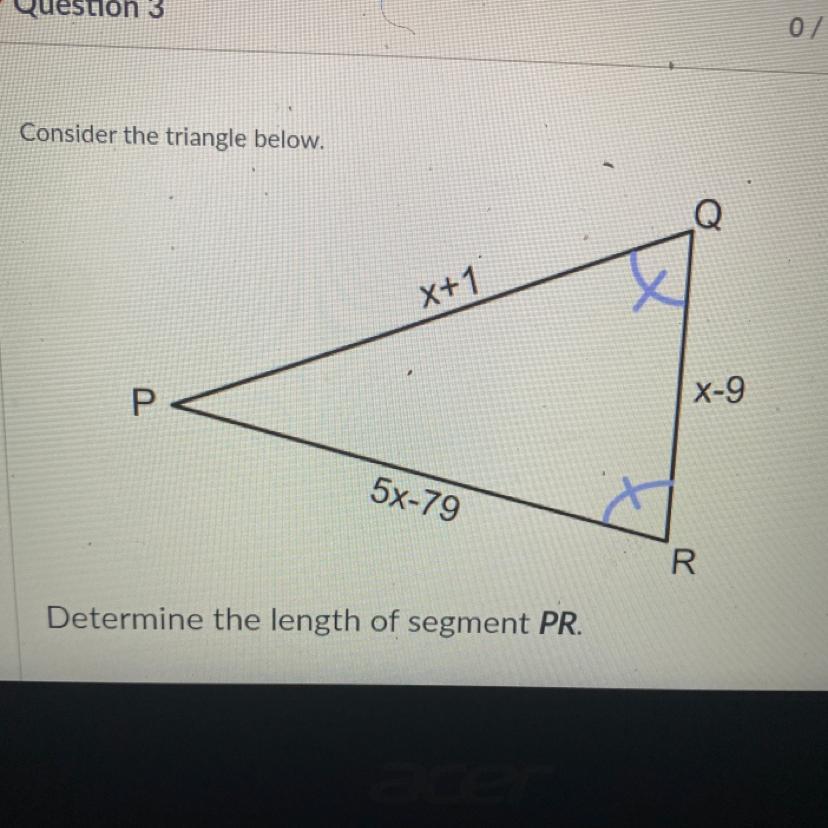
Answers
Answer:
PR=21
Step-by-step explanation:
make x+1 and 5x-79 equal bec it is isosceles triangle. So x+1=5x-79. Then isolate x.
4x=80
x=20
Plug x in the PR equation or PQ equation
5(20)-79
Which equals 21
Determine the type of dilation shown and the scale factor used.
Enlargement with scale factor of 1.5
Enlargement with scale factor of 2.5
Reduction with scale factor of 1.5
Reduction with scale factor of 2.5

Answers
The type of dilation and scale factor in the figure shown is
Enlargement with scale factor of 2.5How to find the type of dilationScale factors are used to increase or decrease image. The situation of increment is usually called magnifying or enlargement.
The given problem is enlargement since the preimage is smaller than the image. Also the scale factor will be greater than 1
Taking a point of reference say side 6 in the preimage and side 15 in the image and solve for the factor, assuming the factor is k
6k = 15
k = 15/6
k = 2.5
hence we say that the scale factor is 2.5
Read more on scale factor here:
brainly.com/question/8159270
#SPJ1
Answer: Enlargement with scale factor of 2.5
Step-by-step explanation: I took the quiz so you don't have too!
This year, the ACT score of a randomly selected student is normally distributed with a mean of 24.4 points and a standard deviation of 4.7 points. Let XX be the ACT score of a randomly selected student and let ¯¯¯XX¯ be the average ACT score of a random sample of size 16.
1. Describe the probability distribution of XX and state its parameters μμ and σσ:
Answers
The probability distribution of the sample mean is approximately normal, with mean of 24.4 points and standard deviation of 1.175 points.
How to obtain the distribution?By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation given by the equation presented as follows: \(s = \frac{\sigma}{\sqrt{n}}\).
The mean is the same as the population mean, of 24.4 points, while the shape is approximately normal.
The standard error is given as follows:
\(s = \frac{4.7}{\sqrt{16}} = 1.175\)
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ4
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. find the diameter of the base of the cylinder
Answers
Answer:
2 cm
Step-by-step explanation:
h = 14 cm
Curved surface area of a right circular cylinder = 88 cm²
2πrh = 88
\(2 * \frac{22}{7}*r*14=88\\\\r = \frac{88*7}{2*22*14}\\\\ r =1 \\\\r = 1 cm\)
Diameter = 2 * r = 2 * 1 = 2 cm
Find the critical numbers of the function on the interval 0≤ θ < 2π.
f(θ) = 2cos(θ) +(sin(θ))^2
Answers
Critical values of the function f(θ) = 2cos(θ) +(sin(θ))² on the interval 0≤ θ < 2π is 0 and π.
Therefore, the answer is 0 and π.
f(θ) = 2cos(θ) +(sin(θ))²
f'(θ) = -2sin(θ) +2sin(θ)cos(θ)
Critical values of f are points at which f' is zero or not defined.
For all values of θ, we can find that f'(θ) is defined.
f'(θ) = 0
-2sin(θ) +2sin(θ)cos(θ) = 0
cos(θ) - 1 = 0 or sin(θ) = 0
cos(θ) = 1
θ = nπ, n = 0, 1, 2, ...
sin(θ) = 0
θ = nπ, n = 0, 1, 2, ...
Therefore in the interval 0 ≤ θ < 2π, critical values are 0 and π.
2π is not there as it is not included in the interval.
To know more on critical values
https://brainly.com/question/36886
#SPJ4
A
If m ZABD = 75° and m/ABC = 40°,
then mZCBD = [?]°
![AIf m ZABD = 75 and m/ABC = 40,then mZCBD = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/U7BpJZbG6ggneMKGBsmj0AoD63wQQYhv.png)
Answers
We see BC is in the middle of the lines AB and BD, therefore mABC + mCBD = mABD.
We're given mABD = 75, mABC = 40.
Therefore, mCBD = mABD - mABC = 75 - 40 = 35.
Answer:
∠CBD = 35°
Step-by-step explanation:
We are told in the question that m∠ABD = 75° and m∠ABC = 40°. We are then asked what the value of m∠CBD is.
As we can see from the diagram, ∠ABD is made up of the angles ABC and CBD. Therefore:
∠ABD = ∠ABC + ∠CBD
⇒ 75° = 40° + ∠CBD
⇒ 75° - 40° = 40° + ∠CBD - 40° [
⇒ 35° = ∠CBD
∴ ∠CBD = 35°
Logan saved $35 from cutting the neighbor’s yard. He earns $10 a week from washing dishes, which he also saves. Which function can be used to find s, the amount of money Logan will have saved at the end of w, weeks of washing dishes?
Answers
the answer is “s = 10w + 35” since he already has 35 but needs to find out how many weeks he washed the dishes :))
Use rounding to estimate the product.
58 x 27
Enter your answer in the box.
Answers
In a recent year, 33.1% of all registered doctors were female. If there were 53700 female registered doctors that year, what was the total number of registered doctors?Round your answer to the nearest whole number.
Answers
It's given that 33.1% of all registered doctors were female, corresponding to 53700 female registered doctors.
It's required to find the total number of registered doctors.
The total number of doctors corresponds to 100%, so we use the inverse percentage calculation:
\(n=\frac{53700}{33.1}\cdot100=162236\)There were 162236 doctors in total
Consider a 2-layer channel with a flat bottom. Consider a domain infinitively wide in
y (practically when you have to write the dispersion relation only kx remains and you can
neglect ly). Show that, in presence of rotation, there is a minimal length for baroclinic
instability to take place
Answers
Rhines criterion implies that there is a minimum length scale for baroclinic instability to take place, which is given by:
L = 2π/kx = 2π[(N² - f₂²)/(f₁² - f₂²)]¹/²
How did this equation evaluate?
In a 2-layer channel with a flat bottom and infinite width in y, the dispersion relation for baroclinic instability is given by:
ω = kx[(f₁² - f₂²)/(N² - f₂²)]¹/²
Where ω is the frequency, kx is the wavenumber in the x-direction, f₁ and f₂ are the Coriolis parameters for the upper and lower layers, and N is the buoyancy frequency.
In the presence of rotation, the minimum length for baroclinic instability to take place is determined by the condition that the frequency ω must be positive. This means that:
(f₁² - f₂²)/(N² - f₂²) > 0
or equivalently:
f₁ > (N²f₂)¹/²
This condition implies that the Coriolis parameter in the upper layer must be greater than the square root of the product of the buoyancy frequency and the Coriolis parameter in the lower layer. This is known as the "Rhines criterion" and represents a necessary condition for the development of baroclinic instability in rotating fluids.
Furthermore, the Rhines criterion implies that there is a minimum length scale for baroclinic instability to take place, which is given by:
L = 2π/kx = 2π[(N² - f₂²)/(f₁² - f₂²)]¹/²
This length scale represents the typical size of the eddies that form due to baroclinic instability in rotating fluids, and is proportional to the inverse square root of the difference between the Coriolis parameters in the upper and lower layers.
Learn more about buoyancy frequency.
brainly.com/question/19168433
#SPJ11
Suppose you need to borrow $90000 at an APR of 5.25% to buy a home.
a) What will your monthly payment be if you opt for a 15-year mortgage?
b) What percentage of your first month's payment will be interest if you opt for a
15 - year mortgage? (Round your answer to two decimal places as a percentage.)
c) How much interest will you have paid by the end of the 15-year loan?
Answers
The first assignment in a statistical computing class involves running a short program. If past experience indicates that 40% of all students will make no programming errors, compute the (approximate) probability that in a class of 50 students a. At least 25 will make no errors [Hint: Normal approximation to the binomial] b. Between 15 and 25 (inclusive) will make no errors
Answers
The approximate probability that at least 25 out of 50 students can be calculated using the normal approximation to the binomial distribution and that between 15 and 25 using the same approximation.
a. To find the probability that at least 25 students will make no errors, we can use the normal approximation to the binomial distribution. The mean of the binomial distribution is np = 50 * 0.4 = 20, and the standard deviation is sqrt(np(1-p)) = \(\sqrt{50*0.4*0.6}\)≈ 3.46.
We can then use these values to approximate the probability using the normal distribution. By standardizing the values, we can calculate the probability of at least 25 students making no errors.
b. To find the probability that between 15 and 25 (inclusive) students will make no errors, we can calculate the probability of fewer than 26 students making no errors and subtract the probability of fewer than 15 students making no errors.
This can also be done using the normal approximation to the binomial distribution, by standardizing the values and calculating the corresponding probabilities.
Using the normal approximation, we can find the approximate probabilities for both scenarios based on the given error rate and the number of students.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A manufacturer has a monthly fixed cost of $40,000 and a product cost of $8 for each unit produced. The products sells for $12/unit.

Answers
Answer:
48,000
Step-by-step explanation:
The cost function by the given data is C(x) = 40,000 + 8x.
We are given that;
Monthly fixed cost = $40,000
The product cost for each unit produced= $8
Now,
The cost function is a function that gives the total cost of producing a certain number of units. The cost function depends on the fixed cost and the variable cost per unit. The fixed cost is the amount of money that the manufacturer has to pay regardless of how many units are produced, such as rent, salaries, utilities, etc. The variable cost per unit is the amount of money that the manufacturer has to pay for each unit produced, such as materials, labor, etc.
In this case, the fixed cost is $40,000 and the variable cost per unit is $8. To find the cost function, we need to add the fixed cost and the product of the variable cost per unit and the number of units.
We can use x to represent the number of units and C(x) to represent the cost function.
Then we have:
C(x) = fixed cost + (variable cost per unit)(number of units)
C(x) = 40,000 + (8)(x)
Therefore, by algebra the answer will be C(x) = 40,000 + 8x.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ2
If A and B are any two events defined on a sample space S of an experiment, then p(A ∩ B) = p(A).p(B)
True or False
Answers
The statement is True only for independent events and False otherwise. The statement "p (A ∩ B) = p(A). p(B)" is not always true for any two events A and B defined on a sample space S of an experiment.
This equation only holds true if A and B are independent events, meaning that the occurrence of one event does not affect the probability of the other event happening. In other words, p(A|B) = p(A) and p(B|A) = p(B).
If A and B are dependent events, meaning that the occurrence of one event affects the probability of the other event happening, then the equation does not hold true. In this case, the probability of A and B occurring together (p(A ∩ B)) would be less than the product of the probabilities of A and B occurring separately (p(A).p(B)).
Therefore, the statement is not always true and depends on whether A and B are independent or dependent events.
Learn more about experiment here:
brainly.com/question/28198971
#SPJ11
Write 15 decreased by 4 times x as a expression.
Answers
Answer: 15-4x
Step-by-step explanation: 15 is being subtracted by 4 multiplied by x (4x).
simplify: -(7z-12b+4c)
Answers
Answer:
-7z+12b-4c or 12b-4c-7c
ellen makes cookies and sells them at the local farmers' market. today, she is going to make batches of her famous cardamom cookies. she has a jar with 2 fluid ounces of cardamom, and her recipe calls for 1 4/5 tablespoons, or 3/10 of a fluid ounce, of cardamom in each batch. how many batches can ellen make with all of her cardamom?
Answers
Ellen can make a maximum of 6 batches of Cardamom cookies with her 2 fluid ounces of cardamom.
Ellen has 2 fluid ounces of cardamom in a jar. Her recipe requires 3/10 of a fluid ounce of cardamom for each batch of cardamom cookies.
We can use division to find the number of batches of cardamom cookies that Ellen can make with all of her cardamom:
2 fluid ounces ÷ (3/10 fluid ounce per batch) = (2/1) ÷ (3/10)
= (2/1) x (10/3)
= 20/3
= 6 2/3
Therefore, Ellen can make 6 batches of cardamom cookies with her 2 fluid ounces of cardamom, with 2/3 of a batch remaining.
Since she cannot make a fraction of a batch, Ellen can make a maximum of 6 batches of cardamom cookies with her 2 fluid ounces of cardamom.
To know more about Cardamom cookies .
https://brainly.com/question/31945877
#SPJ11
Find the distance between the two points rounding to the nearest tenth (if necessary).
(-6, 6) and (-3,3)
Answers
Two waves are described by: 3₁ (2, 1) = (0.30) sin(5z - 200t)] and g (z,t) = (0.30) sin(52-200t) + =] where OA A, 0.52 m and v= 40 m/s OB A=0.36 m and v= 20 m/s OC A=0.60 m and v= 1.2 m/s OD. A = 0.24 m and v= 10 m/s DE A=0.16 m and = 17 m/s and are in meters, and t is in seconds. Calculate the amplitude of the resultant wave and its speed.
Answers
The amplitude of the resultant wave is 0.60 m/s and its speed is 17.64 m/s.
Given,
Two waves are described by:
3₁ (2, 1) = (0.30) sin(5z - 200t)] and
g (z,t) = (0.30) sin(52-200t)
+ =]
where OA A, 0.52 m and v= 40 m/s
OB A=0.36 m and
v= 20 m/s OC
A=0.60 m and
v= 1.2 m/s OD.
A = 0.24 m and
v= 10 m/s
DE A=0.16 m and
= 17 m/s
The amplitude of a wave is the distance from its crest to its equilibrium. The amplitude of the resultant wave is calculated by adding the amplitudes of the individual waves and is represented by A.
The expression for the resultant wave is given by f(z,t) = 3₁ (2, 1) + g (z,t)
= (0.30) sin(5z - 200t)] + (0.30) sin(52-200t)
+ =]
f(z,t) = (0.30) [sin(5z - 200t) + sin(52-200t)
+ =]
Therefore, A = 2(0.30) = 0.60 m/s
The speed of a wave is given by the product of its wavelength and its frequency. The wavelength of the wave is the distance between two consecutive crests or troughs, represented by λ. The frequency of the wave is the number of crests or troughs that pass through a given point in one second, represented by f.
Speed = λf
The wavelengths of the given waves are OA = 0.52 m,
OB = 0.36 m,
OC = 0.60 m,
OD = 0.24 m,
DE = 0.16 m
The frequencies of the given waves are OA :
v = 40 m/s,
f = v/λ
= 40/0.52
= 77.0 Hz
OB : v = 20 m/s,
f = v/λ
= 20/0.36
= 55.6 Hz
OC : v = 1.2 m/s,
f = v/λ
= 1.2/0.60
= 2.0 Hz
OD : v = 10 m/s,
f = v/λ
= 10/0.24
= 41.7 Hz
DE : v = 17 m/s,
f = v/λ
= 17/0.16
= 106.25 Hz
The speed of the resultant wave is the sum of the speeds of the individual waves divided by the number of waves. Therefore,
Speed of the resultant wave = (40 + 20 + 1.2 + 10 + 17)/5
= 17.64 m/s
Hence, the amplitude of the resultant wave is 0.60 m/s and its speed is 17.64 m/s.
To know more about amplitude visit
https://brainly.com/question/2845956
#SPJ11
The amplitude of the resultant wave and its speed are to be determined.
Let's use the formula of the resultant wave, where,
A is amplitude, f is frequency, v is velocity and λ is wavelength of the wave.
A = \([(OA^2 + OB^2 + OC^2 + OD^2 + DE^2 + 2(OA)(OB)(cosθ) + 2(OA)(OC)(cosθ) + 2(OA)(OD)(cosθ) + 2(OA)(DE)(cosθ) + 2(OB)(OC)(cosθ) + 2(OB)(OD)(cosθ) + 2(OB)(DE)(cosθ) + 2(OC)(OD)(cosθ) + 2(OC)(DE)(cosθ) + 2(OD)(DE)(cosθ))]^{1/2\)
where, cosθ = [λ1/λ2] and λ1, λ2 are the wavelength of the two waves.
The velocity of the wave is given by the relation v = fλ
We can calculate the velocity of the resultant wave by using the above formula and calculating the value of wavelength of the wave.
Here, we are given λ for each wave. Speed = 40 m/s
Amplitude of the resultant wave= \([ (0.52^2 + 0.36^2 + 0.6^2 + 0.24^2 + 0.16^2 + 2(0.52)(0.36) + 2(0.52)(0.6) + 2(0.52)(0.24) + 2(0.52)(0.16) + 2(0.36)(0.6) + 2(0.36)(0.24) + 2(0.36)(0.16) + 2(0.6)(0.24) + 2(0.6)(0.16) + 2(0.24)(0.16) )]^{1/2\)
=\([ (0.2704 + 0.1296 + 0.36 + 0.0576 + 0.0256 + 0.3744 + 0.624 + 0.2496 + 0.1664 + 0.1296 + 0.0864 + 0.0576 + 0.144 + 0.096 + 0.0384) ]^{1/2\)
=\([ (2.2768) ]^{1/2\)
= 1.51 m/s
Therefore, the amplitude of the resultant wave is 1.51 m/s and the speed of the wave is 1.51 m/s.
To know more about amplitude visit:
https://brainly.com/question/9525052
#SPJ11
A sales associate farms a neighborhood with 750 homes. The owners seem to list their homes every six years. How many listings should the sales associate obtain if she can list 40% of the homes in the neighborhood
Answers
Answer:
50 homes
Step-by-step explanation:
Given that:
Total Number of homes = 750
Years at which home is listed = 6
Thus average listing per year = (total number of homes / years)
Average listing per year = 750 / 6
Average listing per year = 125 homes
If 40% of homes in the neighborhood can be listed :
0.4 * 125
= 50 homes
Sales associate should obtain listing of 50 homes
Calculation of homes listing obtained by Sales associate
Given : Total 750 houses with listing tendencies every six years.
So, average annual houses listing = 750 / 6 = 125
Also, listings = 40%
Hence, sales associate obtain 40% of 125 = 50
To learn more about Percentage listings, refer https://brainly.com/question/5692146?referrer=searchResults
Use the Distributive Property to expand (−4y−5z)3

Answers
Answer:
-12y -15z
Step-by-step explanation:
3(-4y)= -12y
3(-5z)= -15z
Answer:
D. -12y -15z
Step-by-step explanation: