Find the indicated term 31st term: 12, 7, 2, -3
Answers
So you have to do -5 multiplied by 31 + 17.
The answer= -138
Related Questions
Help please!!!!!!!!!!!

Answers
Answer:
i think your answer is 8.
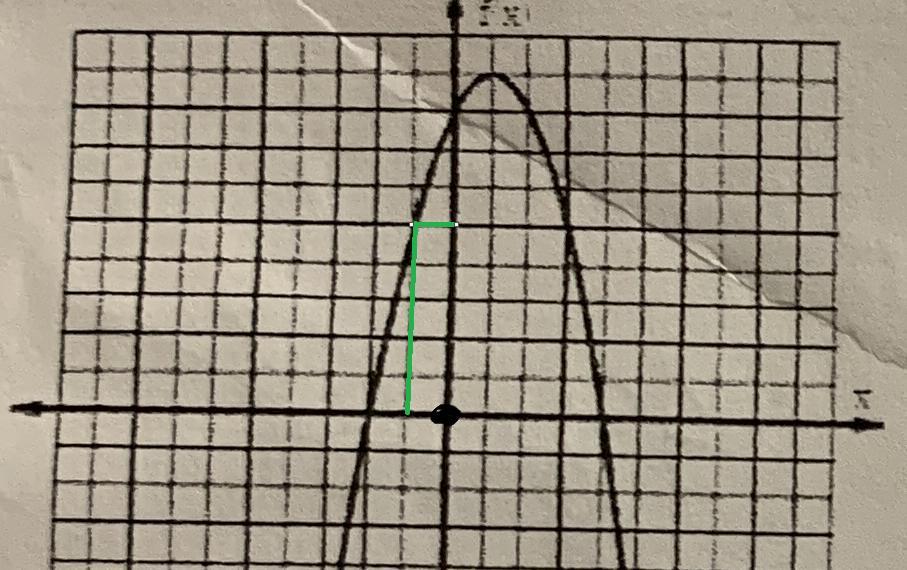
24. Find fl-1).For questions 24-27, use the graph below.25. Find f(4).26. Find f(-3).27. If f(x) = 9, find x.

Answers
Let's start by calculating the value for f(-1).
For this we go to the graph and count the number of squares to the left of the axis to be at -1. In this case f(-1) would be 5.
Now let's calculate f(4)
For this case the value of f(4) would be 0.
Similarly we calculate f(-3). As you can see in the graph it would be 6.
The last scenario would be for when f(x) = 9, we look for that value on the curve and realize that it corresponds to x = 1.



Please help me I'm stuck. I will give 30 points for this one. Given triangle ABC tilde triangle PQR and your scale factor Complete the hotspots for these similar triangles and show work

Answers
The value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
What are similar trianglesSimilar triangles are two triangles that have the same shape, but not necessarily the same size. This means that corresponding angles of the two triangles are equal, and corresponding sides are in proportion.
(1). angle B = 180 - (22 + 90) {sum of interior angles of a triangle}
angle B = 68°
Given that the triangle ∆ABC is similar to the triangle ∆PQR.
(2). PQ/7.5cm = 12cm/18cm
PQ = (12cm × 7.5cm)/18cm {cross multiplication}
PQ = 5cm
(3). 13cm/BC = 12cm/18cm
BC = (13cm × 18cm)/12cm {cross multiplication}
BC = 19.5cm
(4). area of ∆PQR = 1/2 × 12cm × 5cm
area of ∆PQR = 6cm × 5cm
area of ∆PQR = 30cm²
Therefore, the value for the hotspots of the similar triangles ∆ABC and ∆PWR are:
(1). angle B = 68°
(2). PQ = 5cm
(3). BC = 19.5cm
(4). area of ∆PQR = 30cm²
Read more about similar triangles here:https://brainly.com/question/14285697
#SPJ1
consider the solid obtained by rotating the region bounded by the given curves about the x-axis.
y = 2-1/2x,y = 0, x = 1, x = 2
Find the volume V of this solid.
Answers
The volume V of the solid obtained by rotating the region bounded by the given curves about the x-axis is π cubic units.
To find the volume V of the solid obtained by rotating the region bounded by the curves y = 2 - (1/2)x, y = 0, x = 1, and x = 2 about the x-axis, the method of cylindrical shells.
The volume V can be calculated using the following formula:
V = ∫(2πx × h) dx
where h represents the height of the cylindrical shell at each value of x.
The height h can be determined as the difference between the y-values of the curves y = 2 - (1/2)x and y = 0.
The integral,
V = ∫(2πx × h) dx
= ∫(2πx ×(2 - (1/2)x)) dx
= 2π ∫(2x - (1/2)x²) dx
= 2π [(x²) - (1/6)(x³)] evaluated from 1 to 2
Evaluating the definite integral,
V = 2π [(2²) - (1/6)(2³)] - 2π [(1²) - (1/6)(1³)]
= 2π [4 - (1/6)(8)] - 2π [1 - (1/6)(1)]
= 2π [4 - (4/6)] - 2π [1 - (1/6)]
= 2π [4 - (2/3)] - 2π [1 - (1/6)]
= 2π [4/3] - 2π [5/6]
= (8π/3) - (5π/3)
= (3π/3)
= π
To know more about volume here
https://brainly.com/question/28058531
#SPJ4
solve 28/36 = 14/y (please help :( )
Answers
solve the equation 4x^3 + 32x^2 + 42x - 16 = 0, given that one root is equal to the sum of the other two roots
Answers
The solutions to the equation are x = -1, x = -8, and x = 1/2.
How to calculate the valueThe equation 4x³ + 32x² + 42x - 16 = 0 can be divided throuh by 2 as follows:
2x³ + 16x² + 21x - 8 = 0
We can test each of these possible roots by substituting them into the equation and seeing if we get 0. When we substitute -1, we get 0, so -1 is a root of the equation. We can then factor out (x + 1) from the equation to get:
(x + 1)(2x² + 15x - 8) = 0
We can then factor the quadratic 2x² + 15x - 8 by grouping to get:
(x + 8)(2x - 1) = 0
This gives us two more roots, x = -8 and x = 1/2.
Therefore, the solutions to the equation are x = -1, x = -8, and x = 1/2.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
Emilio's dog eats 1/2 of a can of food each day. emilio currently has 2 1/2 cans of dog food. how many days will the current supply of dog food last? write your answer as a fraction or as a whole or mixed number. days
Answers
The current supply of dog food will last for 5 days.
Emilio's dog eats 1/2 of a can of food each day. Emilio currently has 2 1/2 cans of dog food. To determine how many days the current supply will last, we need to find the total number of days it takes to consume the available dog food.
If the dog eats 1/2 can of food each day, we can calculate the number of days the current supply will last by dividing the total amount of dog food by the amount consumed each day.
2 1/2 cans of dog food can be written as 2 + 1/2 = 2.5 cans.
The number of days the current supply will last is given by:
(2.5 cans) / (1/2 can per day)
To divide by a fraction, we multiply by its reciprocal:
(2.5 cans) * (2/1 can per day)
The cans cancel out, leaving us with:
2.5 * 2 = 5
Therefore, the current supply of dog food will last for 5 days.
The current supply of dog food, which is 2 1/2 cans, will last for 5 days based on the dog's consumption rate of 1/2 can per day.
To know more about consumption rate, visit
https://brainly.com/question/32405056
#SPJ11
An ordered pair is a(n) ________ of an equation in two variables if replacing the variables by the coordinates of the ordered pair results in a true statement.
Answers
An ordered pair is a solution of an equation in two variables if replacing the variables by the coordinates of the ordered pair results in a true statement.
In mathematics, an equation in two variables represents a relationship between two quantities. An ordered pair consists of two values, typically denoted as (x, y), that represent the coordinates of a point in a two-dimensional plane.
When these values are substituted into the equation, if the equation holds true, then the ordered pair is considered a solution or a solution set to the equation. This means that the relationship described by the equation is satisfied by the values of the ordered pair. In other words, the equation is true when evaluated with the values of the ordered pair.
Learn more about ordered pair at https://brainly.com/question/29427152
#SPJ11
Consider the sets:
U = {1, 2, {1}, {2}, {1, 2}} A = {1, 2, {1}} B = {{1}, {1, 2}} C = {2, {1}, {2}}
Ƥ (A) is the set:
a.
{⊘, {1}, {2}, {1, 2}, {1, 2, {1}}}
b.
{⊘, {1}, {2}, {{1}}, {1, 2} {1, {1}}, {2, {1}}, {1, 2, {1}}}
c.
{⊘, {1}, {2}, {{1, 2}}, {1, {1}}, {2, {1}}, {1, 2, {1, 2}}}
d.
{⊘, {1}, {2}, {{1}}, {1, {1}}, {2, {1}}, {1, 2, {1}}}
Answers
Ƥ (A) is the set {⊘, {1}, {2}, {{1}}, {1, 2} {1, {1}}, {2, {1}}, {1, 2, {1}}}
To determine Ƥ(A), we need to find the power set of set A, which is the set of all possible subsets of A, including the empty set.
The power set is a set which includes all the subsets including the empty set and the original set itself. It is usually denoted by P. Power set is a type of sets, whose cardinality depends on the number of subsets formed for a given set
Set A = {1, 2, {1}}
The elements of the power set of A, denoted as Ƥ (A), are:
{⊘, {1}, {2}, {{1}}, {1, 2} {1, {1}}, {2, {1}}, {1, 2, {1}}}
Therefore, the correct option is
b. {⊘, {1}, {2}, {{1}}, {1, 2} {1, {1}}, {2, {1}}, {1, 2, {1}}}
To know more about set click here :
https://brainly.com/question/30705181
#SPJ4
Monday, the official exchange rate, in u.s. dollars per dabcoin, is $34. if a customer can spend a maximum of $ 750 on dabcoins and is charged the % what is the greatest number of dabcoins the cus tomer can purchase , rounded to the nearest whole number ?
Answers
The greatest number of dabcoins the customer can purchase, rounded to the nearest whole number is 22 dabcoins.
Given the official exchange rate, in U.S. dollars per dabcoin, is $34 and a customer can spend a maximum of $750 on dabcoins and is charged the percentage. Let's find the greatest number of dabcoins the customer can purchase, rounded to the nearest whole number.
As per the given problem,
Official exchange rate, in U.S. dollars per dabcoin, is $34.
So, cost of 1 dabcoin = $34
The customer can spend a maximum of $750 on dabcoins.
So, $750 is the amount available to purchase dabcoin.
And, charged the percentage is not given so, let's consider it x%
Now, the amount spent on dabcoin can be represented by the product of the cost of 1 dabcoin and the number of dabcoins purchased plus the percentage charged.
Amount spent = (Cost of 1 dabcoin × Number of dabcoins purchased) + (Percentage charged)
According to the problem, the amount spent on dabcoin is limited to $750.
Therefore, (Cost of 1 dabcoin × Number of dabcoins purchased) + (Percentage charged) = $750... (1)
Also, cost of 1 dabcoin = $34.
Now substitute the value of cost of 1 dabcoin in equation (1).
$34 × Number of dabcoins purchased + (Percentage charged) = $750
Now solve for Number of dabcoins purchased.
Number of dabcoins purchased = $750/$34 - Percentage charged / $34
Number of dabcoins purchased = $22.0588235294 - Percentage charged / $34
To find the greatest number of dabcoins the customer can purchase, rounded to the nearest whole number, we need to round off Number of dabcoins purchased.
So, Number of dabcoins purchased = 22 - Percentage charged / $34
To know more about the customer, visit:
https://brainly.com/question/15404115
#SPJ11
The posted speed limit along Elm Street is 25 mph. Homeowners living on Elm Street claim that the
average speed of automobiles traveling on Elm Street is greater than the posted limit of 25 mph and plan to
investigate their claim by measuring the speed of 20 randomly selected cars. If the data support the claim,
the residents plan to ask the city council for more police patrol along Elm Street. Here are the speeds (in
mph) of the 20 cars:
26. 2 22. 9 28. 8 29. 0 24. 8
24. 7 24. 0 24. 4 25. 2 31. 1
25. 6 21. 6 27. 4 25. 6 26. 4
23. 7 28. 2 24. 1 26. 7 26. 8
(a) Is there convincing evidence at the a = 0. 05 significance level that the true mean speed of all cars
traveling on Elm Street is more than 25 mph?
(b) Referring to your conclusion, what type of error may have been made? Describe the error in the
context of this study
Answers
The sample of the speeds of 20 cars and at a 0.05 confidence level, we
have;
(a) There is not enough convincing evidence to suggest that the true mean speed of all cars travelling on Elm Street is more than 25 mph
(b) Type II error
What are the process to test the hypothesis?(a) Based on the given data, using MS Excel, we have;
The sample size, n = 20
The mean, \(\overline x\) = 25.86
The standard deviation of the sample, s = 2.284
The null hypothesis, H₀; \(\overline x\) = 25 mph
Alternative hypothesis, Hₐ; \(\overline x\) > 25 mph
Given that the sample size is less than 30, the t-test is used, and the t-score is found as follows;
\(t= \mathbf{\dfrac{\bar{x}-\mu }{\dfrac{s}{\sqrt{n}}}}\)
Which gives;
\(t=\dfrac{25.86-25 }{\dfrac{2.284}{\sqrt{20}}} \approx \mathbf{1.684}\)
Using a graphing calculator, we have;
The probability ≈ 0.054
The critical-t ≈ 1.729
Given that the probability is larger than the significance level, we fail to
reject the null hypothesis.
There is not enough convincing statistical evidence to conclude that the
true mean of all cars travelling on Elm Street is more than 25 mph.
(b) The type of error is Type II error, given that there is a possibility that
the null hypothesis is failed to be rejected when it is actually false.
Given that the sample size is less than 30, it may be insufficient for the
Central Limit Theorem to be in effect.
Learn more about statistical hypothesis testing here:
https://brainly.com/question/14042255
(x-y)^p (x^2+y^2+q+y)
Answers
The simplified expression of the expression \((x - y)^p(x^2 + y^2 + q - y)\)while done the simplification through binomial theorm.
\((x - y)^p(x^2 + y^2 + q - y)\)
Expanding the first term using the binomial theorem, we get:
\((x - y)^p = \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^k\)
where [ p choose k ] is the binomial coefficient, given by p! / (k! × (p-k)!).
Substituting this expansion into the original expression, we get:
\(\sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} (x^2 + y^2 + q + y)\)
Expanding the last term, we get:
\(\sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} (x^2 + y^2) + \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} (q+y)\)
The first term can be simplified by distributing the x² and y² terms:
\(\begin{aligned} &\sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} x^{2} + \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} y^{2} \\&= x^{2} \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} + y^{2} \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} \\&= x^{2}(x-y)^{p} + y^{2}(x-y)^{p} \\&= (x^{2}+y^{2})(x-y)^{p}\end{aligned}\)
The second term can be simplified by distributing the x and y terms:
\(\begin{aligned} &\sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} q + \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} y \\&= q \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} - y \sum_{k=0}^{p} {p \choose k} x^{p-k} (-y)^{k} \\&= q (x-y)^{p} - y (x-y)^{p} \\&= (q-y) (x-y)^{p}\end{aligned}\)
Putting these simplified terms together, we get:
\(\begin{aligned}(x-y)^p \cdot (x^2 + y^2 + q - y) &= (x-y)^p \cdot [(x^2 + y^2) + (q - y)] \\&= (x-y)^p \cdot (x^2 + y^2) + (x-y)^p \cdot (q - y) \\&= (x^2 + y^2) \cdot (x-y)^p + (q - y) \cdot (x-y)^p \\&= (x^2 + y^2 + q - y) \cdot (x-y)^p\end{aligned}\)
Therefore, the simplified expression is \((x-y)^p \cdot (x^2 + y^2 + q - y)\)
Learn more about binomial:
https://brainly.com/question/30339327
#SPJ1
BRAINLIEST
Two questions to solve
Please no trolling

Answers
Answer:
Step-by-step explanation:
question 13:
the triangle with x is a 30-60-90 triangle which means
x= 17√3
then the traingle with y and z is a 45-45 triangle
z=34
y= 34√2
question 14:
x= 18√3
z=9
y= 18
Randois samples of four different models of cars were selected and the gas mileage of each car was meased. The results are shown below Z (F/PALE ma II # 21 226 22 725 21 Test the claim that the four d
Answers
In the given problem, random samples of four different models of cars were selected and the gas mileage of each car was measured. The results are shown below:21 226 22 725 21
Given that,The null hypothesis H0: All the population means are equal. The alternative hypothesis H1: At least one population mean is different from the others .
To find the hypothesis test, we will use the one-way ANOVA test. We calculate the grand mean (X-bar) and the sum of squares between and within to obtain the F-test statistic. Let's find out the sample size (n), the total number of samples (N), the degree of freedom within (dfw), and the degree of freedom between (dfb).
Sample size (n) = 4 Number of samples (N) = n × 4 = 16 Degree of freedom between (dfb) = n - 1 = 4 - 1 = 3 Degree of freedom within (dfw) = N - n = 16 - 4 = 12 Total sum of squares (SST) = ∑(X - X-bar)2
From the given data, we have X-bar = (21 + 22 + 26 + 25) / 4 = 23.5
So, SST = (21 - 23.5)2 + (22 - 23.5)2 + (26 - 23.5)2 + (25 - 23.5)2 = 31.5 + 2.5 + 4.5 + 1.5 = 40.0The sum of squares between (SSB) is calculated as:SSB = n ∑(X-bar - X)2
For the given data,SSB = 4[(23.5 - 21)2 + (23.5 - 22)2 + (23.5 - 26)2 + (23.5 - 25)2] = 4[5.25 + 2.25 + 7.25 + 3.25] = 72.0 The sum of squares within (SSW) is calculated as:SSW = SST - SSB = 40.0 - 72.0 = -32.0
The mean square between (MSB) and mean square within (MSW) are calculated as:MSB = SSB / dfb = 72 / 3 = 24.0MSW = SSW / dfw = -32 / 12 = -2.6667
The F-statistic is then calculated as:F = MSB / MSW = 24 / (-2.6667) = -9.0
Since we are testing whether at least one population mean is different, we will use the F-test statistic to test the null hypothesis. If the p-value is less than the significance level, we will reject the null hypothesis. However, the calculated F-statistic is negative, and we only consider the positive F-values. Therefore, we take the absolute value of the F-statistic as:F = |-9.0| = 9.0The p-value corresponding to the F-statistic is less than 0.01. Since it is less than the significance level (α = 0.05), we reject the null hypothesis. Therefore, we can conclude that at least one of the population means is different from the others.
To know more about hypothesis visit :
https://brainly.com/question/29576929
#SPJ11
During one week, David worked 16 hours at his normal hourly rate and
7 hours at his time and a half rate. His total pay for the week was
$848.
What is David’s normal hourly rate?
Answers
Answer:
43.49
Step-by-step explanation:
let his normal hourly rate be x
16x+7x/2=848
39x/2=848
x=848 ÷ 39/2
=43.48717
What is the distance between the points (8, 12) and (1, 3)? If necessary, round
your answer to two decimal places.
O A. 130 units
B. 11.40 units
C. 12.08 units
D. 146 units
Answers
Answer:
B
Step-by-step explanation:
(8,12)=(x1, y1)
(1,3)=(X2, y2)
distance=√(x2-x1)^2+(y2-y1)^2
=√(1-8)^2+(3-12)^2
=√(49+81)
√130
=11.40
Does (2, 4) make the equation y = –6x true?
Answers
Answer:
No
Step-by-step explanation:
When \(x=2\), \(y=-6(2)=-12\), not \(4\).
If f(x) = 2x + 30 and g(x) = x2 + 5x - 10, what values of x will make f(x) = g(x)?
Answers
Answer:
x=5 and x=-8
Step-by-step explanation:
take f(x)=g(x)
2x+30 = x2 +5x-10
you get above values of x
Select the correct answer. .
Which number has a repeating decimal form?
A 15
B 11/25
C 3/20
D 2/6
Answers
Answer:
B
Step-by-step explanation:
I say B because 2 divided by 6 is .333333333 and so on and so forth.
Hope this helped!!
६
{even numbers between 4 and 34}
C = {6, 10, 16, 22, 24, 28, 30, 32, 34}
D = {4, 6, 10, 16, 18, 24, 28, 30, 34}
List the elements in C' n D'
C'nD' = {
Separate answers with commas
=
'
Answers
Answer:
C'nD' = {5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33}
Step-by-step explanation:
C' is the complement of C, which contains all the numbers not in C. Since C contains all the even numbers between 4 and 34, C' contains all the odd numbers between 4 and 34 and 4 and 36.
C' = {4, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 36}
Similarly, D' contains all the numbers that are not in D, which are the even numbers between 5 and 33, as well as 4 and 34.
D' = {5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33}
The intersection of C' and D' contains only the numbers in both C' and D'. Therefore,
C' n D' = {5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33}
So, the elements in C' n D' are all odd numbers between 5 and 33.
What is an equation of the line that passes through the points (-5, 1)(−5,1) and (5, 3)(5,3)?
Answers
Answer:
x=-5 i think
Step-by-step explanation:
Paul's time for swimming in the Ironman triathlon was 1 hour 25 minutes. Her time for viking was 5 hours longer than her swimming time. She ran for 4 hours 50 minutes. Assuming she took no breaks in between each event, how long did it take her to complete all three parts of the race?1 hour =60 minutes
Answers
It took Paul a total of 12 hours and 40 minutes to complete all three parts of the Ironman triathlon.
Paul’s time for swimming in the Ironman triathlon was 1 hour 25 minutes. Her time for biking was 5 hours longer than her swimming time, so her biking time was (1 hour + 5 hours) = 6 hours 25 minutes. She ran for 4 hours 50 minutes. The total time it took her to complete all three parts of the race is (1 hour 25 minutes) + (6 hours 25 minutes) + (4 hours 50 minutes) = 12 hours 40 minutes.
Learn more about addition here: brainly.com/question/29464370
#SPJ4
find the measure of two supplementary angles if the difference between the measure of the two angles is 35
Answers
Answer:
the sum adds up to 180
hope this helped!!.. <3
Step-by-step explanation:
180=x+x+35
180=2x+35
-35 -35
145=2x
/2 /2
72.5=x
The two angles are:
72.5
107.5
How do you dilate points at a point?
Answers
To dilate a point at a point, you start by selecting a center of dilation and a scale factor.
Then, for each point that you want to dilate, you do the following:
Draw a line segment from the center of dilation to the point.Multiply the length of this line segment by the scale factor.Draw a line segment from the center of dilation to the new point, using the length that you just calculated.The new point is the point that you arrive at when you complete this line segment.For example, if you wanted to dilate point P by a scale factor of 2, with the center of dilation at O, you would draw a line segment from O to P, double its length, and then draw a new line segment from O to the new point, using the new length that you calculated. The new point would be the point that you arrive at when you complete this line segment.
Learn more about Scale Factor here:
https://brainly.com/question/25722260
#SPJ4
Hi! whats 6666666 × 727272772
Answers
Answer: 4.8484847e+15
Step-by-step explanation:
Answer:
6666666 × 727272772 = 4,848,484,661,818,152
what are the possible angles between two unit vectors u and v if ∥u × v∥ = 1 2 ?
Answers
the magnitude of the cross product of two unit vectors u and v is 1/2, the possible angles between them are π/6 (or 30°) and 5π/6 (or 150°).
The magnitude of the cross product of two vectors u and v is equal to the area of the parallelogram formed by the two vectors. Therefore, the magnitude of the cross product of two unit vectors u and v is equal to the area of the parallelogram formed by the two vectors, which is also equal to the sine of the angle between them. In other words:
∥u × v∥ = sin(θ)
where θ is the angle between the two vectors. If ∥u × v∥ = 1/2, then we have:
1/2 = sin(θ)
This equation has two solutions: θ = π/6 and θ = 5π/6. Therefore, the possible angles between two unit vectors u and v are π/6 and 5π/6, or approximately 30° and 150°.
To see why there are two solutions, we can look at the unit circle, where sine is positive in the first and second quadrants. The angle θ between u and v can lie in either the first or second quadrant, giving us two possible values for sine. These correspond to the angles π/6 and 5π/6, respectively.
In summary, if the magnitude of the cross product of two unit vectors u and v is 1/2, the possible angles between them are π/6 (or 30°) and 5π/6 (or 150°).
To know more about cross product click here:
brainly.com/question/29164170
#SPJ4
42. Find the equation of the sphere with center C(−2,3,7) that is tangent to the plane 2x+3y−6z=5.
Answers
To find the equation of the sphere tangent to the plane 2x + 3y - 6z = 5 with center C(-2, 3, 7), we need to find the radius of the sphere. The equation of the sphere is (x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36.
The distance from the center of the sphere to the plane is equal to the radius. We can use the formula for the distance between a point (x, y, z) and a plane Ax + By + Cz + D = 0:
Distance = |Ax + By + Cz + D| / sqrt(A^2 + B^2 + C^2)
In this case, the plane equation is 2x + 3y - 6z - 5 = 0. Plugging in the coordinates of the center C(-2, 3, 7) into the formula, we have:
Distance = |2(-2) + 3(3) - 6(7) - 5| / sqrt(2^2 + 3^2 + (-6)^2)
= |-4 + 9 - 42 - 5| / sqrt(4 + 9 + 36)
= |-42| / sqrt(49)
= 42 / 7
= 6
So, the radius of the sphere is 6.
The equation of a sphere with center C(-2, 3, 7) and radius 6 is:
(x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 6^2
Simplifying further, we have:
(x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36
Therefore, the equation of the sphere is (x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36.
Learn more about radius here
https://brainly.com/question/24375372
#SPJ11
select the correct answer consider these functions f(x)=3x-7 g(x)=X +1/x-1 what is the value of f(g(3))
Answers
Answer:
Me and my massive brain, among other massive things of mine, believe it to be -1
Step-by-step explanation:
The value of the function F(g(x) will be equal to (7 / 2).
What is a function?A function is defined as the expression that set up the relationship between the dependent variable and independent variable.
Given functions are:-
f(x)=3x-7 g(x)= x +(1/x-1)The function F(g(x) is written as :-
F(g(x) = 3 [ x + ( 1 / ( x-1 )) -7 ]
F(g(x) = 3 [ (3 + (1/2) - 7 ]
F(g(x) = 3 (7 / 2 ) -7
F(g(x) = ( 21/2) - 7
F(g(x) = ( 21-14 ) ( 2 )
F(g(x) = ( 7/2 )
Therefore the value of the function F(g(x) will be equal to (7 / 2).
To know more about function follow
https://brainly.com/question/25638609
#SPJ2
Use the Pythagorean Theorem to find the diagonal.
a- 60
b- 84.85
c- 10.95
d- 7.74

Answers
Answer:
84.85
Step-by-step explanation:
\( {a}^{2} + {b}^{2} = {c}^{2} \)
\( {60}^{2} + {60}^{2} = {c}^{2} \\ 3600 + 3600 = {c}^{2} \\ 7200 = {c}^{2} \)
now we should find the square root of 7200 to find c
\( \sqrt[]{7200} = 85.85.....\)
Joe wants to use the hiking Club funds to purchase new Walking Stick for each of its 19 members. The sticks cost $26 each The Club has $480 and there's enough money to buy eat remember a new Walking Stick? if not how much more money is needed ?
Answers
ok
1.- Calcualte the total price for 19 sticks
price = 19 x 26
= $494
2.- Conclusion
there is not enough money to buy the sticks the total cost is
$494 and he only has $480.
3.- He needs 494 - 480 = $14 more money