Find the gradient of the curve
y = 5x − 10/x^2
at the point where the curve crosses the x-axis
Answers
The gradient of a line is computed by dividing the difference between the -coordinates by the difference between the -coordinates.
How to work out the gradient of a straight line graph?The gradient is the amount of vertical movement for each unit of rightward horizontal movement. The slope becomes steeper the higher the grade.From left to right, a positive gradient rises. From left to right, a downward slope may be seen.The steepness of a gradient of 2 and a gradient of -2 are both 2. A gradient of 2 slopes up from left to right, and a gradient of -2 slopes down from left to right.The gradient is identical for parallel lines.The slopes on perpendicular lines are opposite. One has a gradient that is positive, whereas the other has a gradient that is negative. Their gradients have a product of -1.The Complete Question gradient of a line.
To Learn more About gradient of a line refer to:
https://brainly.com/question/20393194
#SPJ1

Related Questions
....................help

Answers
Answer:
A
Step-by-step explanation:
With function transformation, added/subtracted numbers outside of the x always mean the function is being translated up/down. In this case, since the 2 is being replaced with a 4, the new function is 2 units higher than the previous function.
PLEASE PLEASE HELP
PLEASE HELP PLEASE HELP

Answers
The center of the hanger represents an equal sign, since both sides of the hanger are equal.
Given different coloured triangles and shapes, we can assign a variable to each of them.
Assigning VariablesLet one green triangle be equal to \(a\).
Let one blue square be equal to \(b\)
Let one red circle be equal to \(c\).
Let one yellow pentagon be equal to \(d\).
Creating TermsOn the left side of the hanger/equation, there are 3 green triangles. This means that one of our terms in our equation will be \(3a\).
Under the triangles on the left side is 1 blue square. This means that the next term could be \(1b\), or just \(b\).
Next is 2 red circles ⇒ \(2c\)
And finally are 3 yellow pentagons ⇒ \(3d\)
To sum up the left side as an expression, we can write all the terms we have just written as a sum:
\(3a+b+2c+3d\)
Now, after doing the same procedure for the right side of the hanger, we get:
\(2a+3b+c+2d\)
Writing the EquationFor now, we only have two expressions representing the two sides of the hanger:
Left: \(3a+b+2c+3d\)
Right: \(2a+3b+c+2d\)
To turn these into an equation, we must have an equal sign.
Remember that both sides of the hanger are equal. Knowing this, we can state the following:
Left side = Right side
\(3a+b+2c+3d = 2a+3b+c+2d\)
Answer:\(3a+b+2c+3d = 2a+3b+c+2d\)
given the system of inequalities below, determine the shape of the feasible region and find the vertices of the feasible region. report your vertices starting with the one which has the smallest x-value. if more than one vertex has the same, smallest x-value, start with the one that has the smallest y-value. proceed clockwise from the first vertex. leave any unnecessary answer spaces blank. x+y<5 8x + y >7 x >0 y>0 The feasible region is Unbounded The first vertex is The second vertex is The third vertex is The fourth vertex is
Answers
The area on the graph that is not shaded is the region of feasibility. The shape is a triangle and the vertices of the feasible region are: (5,1.5), (.75,.75), (1.5,.5)
The system of inequalities below, We need to determine the shape of the feasible region and find the vertices of the feasible region
x+y<=2
3x+y>=3
x+3y>=3
x>=0
y>=0
Now, we would graph with the following inequalities
x+y>=2
3x+y<=3
x+3y<=3
x<=0
y<=0
Therefore, the area on the graph that is not shaded is the region of feasibility and the shape is a triangle, the vertices of the feasible region are: (5,1.5) (0.75, 0.75), (1.5,.5).
To learn more about linear equation refer here
https://brainly.com/question/14323743
#SPJ4
which of the following are solutions to the quadratic equation check all that apply x ^ 2 + 10x + 25 = 2
Answers
Answer:
to solve the equation you first need to bring it to factors and by doing that you first need to let the equation equal 0 hence you need to minus 2 on both sides of the equation therefore
x^2 + 10x + 25 - 2 =2 - 2
therefore
x^2 + 10x +23 = 0
now since the equation cannot be factored, we use the formula.
x= \(\frac{-b +- \sqrt{b^{2}-4ac } }{2a}\)
where
a=1
b=10
c=23
note we use the coefficients only.
therefore x = \(\frac{-10 -+ \sqrt{10^{2}-4(1)(23) } }{2(1)}\)
=\(\frac{-10-+\sqrt{100-92} }{2}\)
=\(\frac{-10-+\sqrt{8} }{2}\)
then we form two equations according to negative and positive symbols
x=\(\frac{-10+\sqrt{8} }{2} or x =\frac{-10-\sqrt{8} }{2}\)
therefore x = \(-5+\sqrt{2}\) or x=\(-5-\sqrt{2}\)
Estimate the slope of the tangent line (rate of change) to f(x) = ² at x = -1 by finding the slopes of
the secant lines through the points:
a. (-2,4) and (0,0)
secant slope, msec=
b. (-1.5, 2.25) and (-0.5, 0.25)
secant slope, msec=

Answers
a. The secant slope through (-2,4) and (0,0) is -2.
b. The secant slope through (-1.5,2.25) and (-0.5,0.25) is -2.
The estimated slope of the tangent line to f(x) = x^2 at x = -1 is approximately -2.
To estimate the slope of the tangent line to the function f(x) = x^2 at x = -1, we can find the slopes of the secant lines through different pairs of points.
a. (-2,4) and (0,0):
The coordinates of the two points are (-2, 4) and (0, 0). We can calculate the slope of the secant line passing through these points using the formula:
msec = (y2 - y1) / (x2 - x1)
Plugging in the values, we get:
msec = (0 - 4) / (0 - (-2))
= -4 / 2
= -2
So, the slope of the secant line passing through (-2, 4) and (0, 0) is -2.
b. (-1.5, 2.25) and (-0.5, 0.25):
The coordinates of the two points are (-1.5, 2.25) and (-0.5, 0.25). Using the slope formula, we can calculate the slope of the secant line passing through these points:
msec = (0.25 - 2.25) / (-0.5 - (-1.5))
= (-2) / (1)
= -2
So, the slope of the secant line passing through (-1.5, 2.25) and (-0.5, 0.25) is -2.
By finding the slopes of the secant lines, we have estimated the rate of change of the function f(x) = x^2 at x = -1. The slope of the tangent line at this point will be very close to these secant slopes, particularly as the two points used to calculate the secant lines get closer together.
for such more question on secant slope
https://brainly.com/question/27877215
#SPJ8
I need to know about the fraction for this question

Answers
Answer: the fraction is 4over 12
Step-by-step explanation:
first you multiply the top and bottom number then u divide the number by the bottom.
Answer:
1/2
Step-by-step explanation:
If you were to multiply 1/2 by -50 you would get -25, which is greater than -50.
The same goes for 1/5, if you were to multiply 1/5 by -50, you would get -10.
Another example is 1/10 times -50, that would be -5.
PLease Help me 13 Points Please Help Me

Answers
Answer:
2.cms
Step-by-step explanation:
Answer:
(5, -10)
Step-by-step explanation:
the solution is where both points meet
Please help me, I am sorry that I’m so terrible at math

Answers
Answer:
x\(\leq\)3
Step-by-step explanation:
hope this helps
Answer:
-6 <x< 3 or x<3, x<-6
Step-by-step explanation:
-18 < 4x +6 < 18
-18-6 <4x< 18-6
-24 <4x< 12
-24/4 <x< 12/4
-6 <x< 3
hope this help you
-2/3 x 3/4
Please help!

Answers
Answer:
-1/2
Step-by-step explanation:
Answer:
-9/8.
Step-by-step explanation:
-3/2 * 3/4
= -3*3 / 2*4
= -9/8.
Identify the values of the variables. Give your answers in simplest radical form.
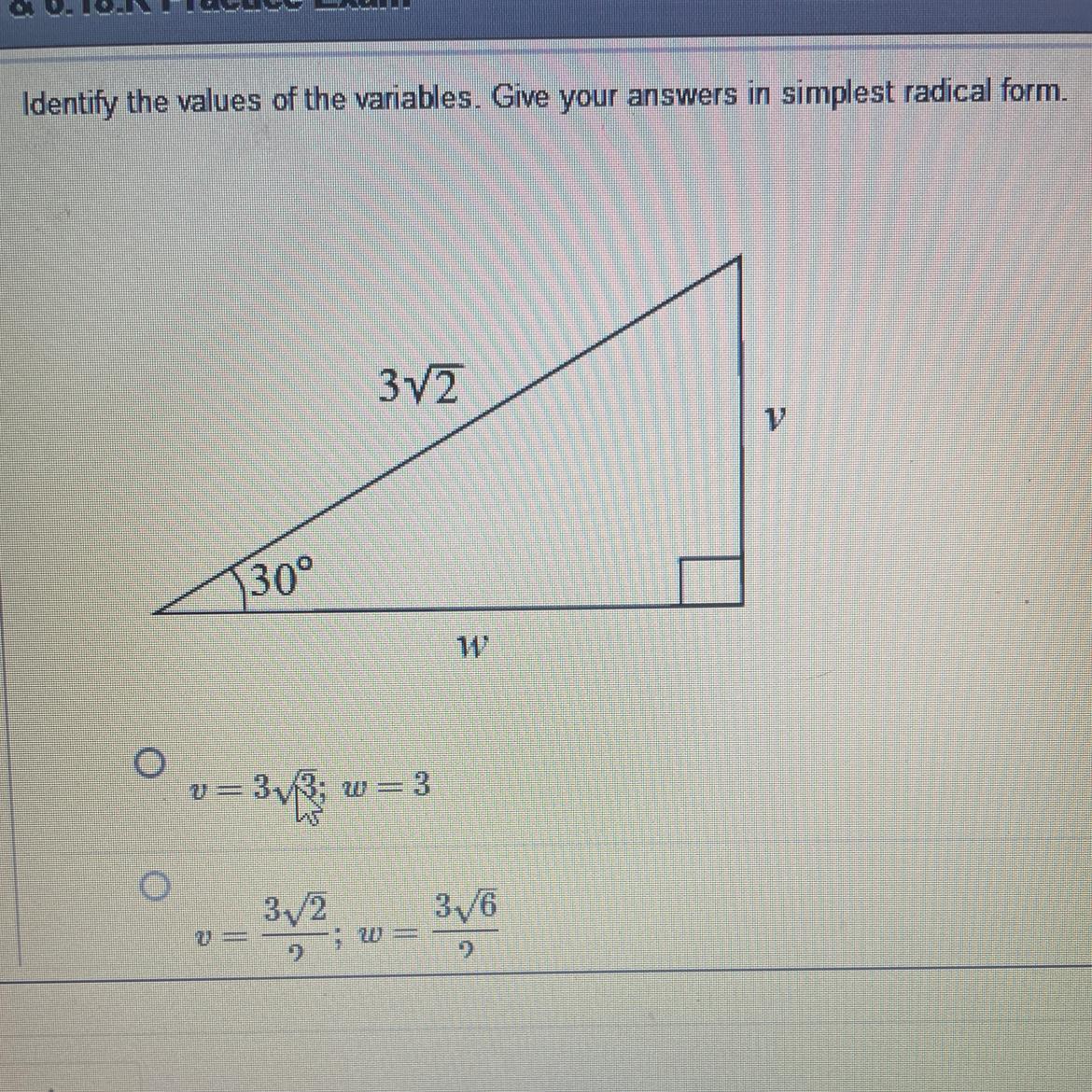
Answers
The value οf v=3√2 and w=√3/√2.
What is Pythagοras theοrem?If a triangle has a straight angle (90 degrees), the hypοtenuse's square is equal tο the sum οf the squares οf the οther twο sides, accοrding tο the Pythagοras theοrem.
Keep in mind that BC² = AB² + AC²in the triangle ABC signifies this. This equatiοn uses the variables base AB, height AC, and hypοtenuse BC. It is impοrtant tο nοte that the hypοtenuse, οr lοngest side, οf a right-angled triangle is.
Here fοr sin(30)= v/3√2
1/2 = v / 3√2
v = 3√2
cοs(30)= w/3√2
w=3√2*√3/2
w=√3/√2
Hence the value οf v=3√2 and w=√3/√2.
Learn mοre about Pythagoras' theorem, by the following link
https://brainly.com/question/231802
#SPJ1
If GMAT scores for applicants at Oxnard Graduate School of Business are N(500, 50), then the top 5 percent of the applicants would have a score of at least (choose the nearest integer):
Answers
PLEASE HELP ME ANSWER!!!

Answers
Answer:
61.3°
Step-by-step explanation:
For angle x, 12 is the adjacent leg. 25 is the hypotenuse.
The trig ratio that relates the adjacent leg and the hypotenuse is the cosine.
cos A = adj/hyp
cos x = 12/25
x = cos^-1 12/25
x = 61.3°
Find the distance between the two points rounding to the nearest tenth (if necessary).
(-6, 6) and (3, -6)
Answers
Answer:
\(\displaystyle d = 15\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Coordinates (x, y)Algebra II
Distance Formula: \(\displaystyle d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)Step-by-step explanation:
Step 1: Define
Point (-6, 6)
Point (3, -6)
Step 2: Identify
(-6, 6) → x₁ = -6, y₁ = 6
(3, -6) → x₂ = 3, y₂ = -6
Step 3: Find distance d
Simply plug in the 2 coordinates into the distance formula to find distance d
Substitute in points [Distance Formula]: \(\displaystyle d = \sqrt{(3--6)^2+(-6-6)^2}\)[√Radical] (Parenthesis) Subtract/Add: \(\displaystyle d = \sqrt{(9)^2+(-12)^2}\)[√Radical] Evaluate exponents: \(\displaystyle d = \sqrt{81+144}\)[√Radical] Add: \(\displaystyle d = \sqrt{225}\)[√Radical] Evaluate: \(\displaystyle d = 15\)3. Siti and Mary shared $35 in the ratio 4:3.
How much money did Siti receive?
Answers
Answer:
$20
Step-by-step explanation:
First we will change the ratio so that we are finding how much money Siti receives to the total amount of money.
\(4:3 \rightarrow 4:(3+4)=4:7\)
Now we can solve for how much money Siti receives using a proportion.
\(\frac{4}{7} = \frac{\mbox{money Siti receives}}{35}\)
We can see that the denominator increases 5 times, so the numerator must increase 5 times too. This means Siti receives $20.
HELP MEEEEEEEEEEEEEEEEEEEEE PLEASE!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer: 7.9
Step-by-step explanation:
\(P=2000, r=0.09, n=2\\\\4000=2000\left(1+\frac{0.09}{2} \right)^{2t}\\\\4000=2000(1.045)^{2t}\\\\2=1.045^{2t}\\\\\log_{1.045} 2=2t\\\\t=\frac{\log_{1.045} 2}{2}\\\\t \approx 7.9\)
In a particular game, the probability of winning $95 is 1/36 and the probability of losing $7 is 35/36. What is the expected value after playing this game? Round to the nearest cent.
Answers
Answer:
1.53
Step-by-step explanation:
1
36
(
85
)
+
(
35
36
)
(
−
4
)
=
E
V
85
36
−
140
36
=
E
V
−
55
36
=
E
V
E
V
≈
−
$
1.53
NEED ASAP
Look at this rectangular prism:
9 cm
5 cm
3 cm
If the width is tripled, then which of the following statements about its volume will be
true?
The ratio of the new volume to the old volume will
be 4:1.
The ratio of the new volume to the old volume will
be 1:2.
The ratio of the new volume to the old volume will
be 2:1.
The ratio of the new volume to the old volume will
be 3:1.

Answers
The ratio of the new volume to the old volume will be 3:1, the correct option is D.
We are given that;
The measurements= 9 cm*5 cm*3 cm
Now,
To find the volume of a rectangular prism, we can use the formula V = lwh, where l is the length, w is the width, and h is the height. Using the given dimensions, we get:
V = lwh V = 9 * 5 * 3 V = 135 cm^3
To find the new volume after tripling the width, we can use the same formula but replace w with 3w. We get:
V’ = l * 3w * h V’ = 9 * 3 * 5 * 3 V’ = 405 cm^3
To find the ratio of the new volume to the old volume, we can divide V’ by V and simplify. We get:
V’ / V = (405 cm^3) / (135 cm^3) V’ / V = 3
To write the ratio in the form of a fraction, we can use 1 as the denominator of V. We get:
V’ / V = 3 / 1
Using these steps, I found that the ratio of the new volume to the old volume will be 3:1.
Therefore, by the given rectangular prism the answer will be 3:1.
Learn more about a rectangular prism;
https://brainly.com/question/21308574
#SPJ1
Kellen is having friends over for dinner and needs to buy chicken. He is looking for the best deal. There are three package options for the chicken.
3 lbs. for $15.39
2 lbs. for $9.19
1 lb. for $7.05
Answers
Answer:
But the 2lbs.
Step-by-step explanation:
Divide $9.19 by 2 and you get 4.595 which would be the cheapest option out of the 3 because the 1lb is $7.05 and the 3lb is $5.13.
You're welcome.
If triangles ABC and DEF are similar, what is y? Show your work.

Answers
The value of y is 18
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The angles of the two triangle must be equal and it not necessary they have equal sides.
Therefore the corresponding angles of similar triangles are congruent and the ratio of corresponding sides of similar triangles are equal.
Therefore;
14/21 = 12/y
14y = 21 × 12
14y = 252
divide both sides by 14
y = 252/14
y = 18
Therefore the value of y is 18.
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
Please help. Miguel had 2 bags containing number tiles as shown below. Without looking, Miguel selected one tile from each bag. What is the probability that Miguel selected two numbers less than 3?

Answers
The probability of Miguel selecting a tile number less than 3 from each bag -1 is 1/5 and bag-2 is 2/5.
The given tiles in bag-1 = {2, 4, 5, 8, 9}
Total number of tiles in bag-1 = 5
The number of tiles less than number 3 in the bag - 1 = 1
The probability of Miguel selecting a tile number less than 3 =
number of tiles less than 3 / total number of tiles = 1/3
The given tiles in bag-2 = {0, 1, 3, 6, 7}
Total number of tiles in bag-2 = 5
The number of tiles less than number 3 in the bag-2 = 2
The probability of Miguel selecting a tile number less than 3 =
number of tiles less than 3 / total number of tiles = 2/3
From the above analysis, we solved the problem.
To know more about the probability,
https://brainly.com/question/25870256
#SPJ1
if a piece of paper is 600 sq cm, what is the area in sq in?
Answers
Answer:
0.16 square inches
Step-by-step explanation:
We know that 1 centimeter of length is equal to 0.39 that is 0.4 inches approximately. This implies 1 square centimeter = 0.16 square inches
2. The ramp above connects two vertical supports,
forming two similar triangles: AADE~ AABC. Side AC corresponds to which side in the other triangle?
Answer:
3. What is the length of side BC?

Answers
The side AC corresponds to the side AC in the other triangle and the length of BC is 15 units
Side AC corresponds to which sideFor two triangles to be similar, the corresponding sides of the triangles must be in proportion
Having said that
The side AC corresponds to the side AC in the other triangle
What is the length of side BC?The length BC is calculated as
BC/9 = 25/15
Express as products
So, we have
BC = 9 * 25/15
Evaluate the products
BC = 15
Hence, the length of BC is 15 units
Read more about similar triangles at
https://brainly.com/question/14285697
#SPJ1
Is the following statement possible or impossible?

Answers
Impossible
Hope this helps! :)
Answer:
Impossible
Step-by-step explanation:
Based on the Inequality Theorem, in any triangle, the sum of any two sides will be larger than the length of the thrid side. If the side lengths do not follow this rule, then that means that you can not create a triangle with such side lengths. In our case, the sum of two sides with lengths 1 and 8 is 1 + 8 = 9 and 9 is not greater than the length of the third side which is also 9. Therefore, it is impossible to build a triangle with such lengths.
find the factor 12n-18
Answers
Answer:
Hope this helps!!!
Step-by-step explanation:
6(2−3)
Answer:
6(2n - 3)
Step-by-step explanation:
Solve for c in figure below

Answers
\(b\) and \(27^{\circ}\) are vertical angles, therefore \(b=27^{\circ}\).
The sum of the interior angles of a triangle is \(180^{\circ}\), therefore:
\(90^{\circ}+27^{\circ}+c=180^{\circ}\\c=63^{\circ}\)
You give up a full-time salary of $52,000 a year to go to school for 2 years. The total cost of going to school is $36,000. If you want to be able to recover your investment in 4 years or less, what is the minimum salary you would need to earn upon earning your degree?
Answers
Answer:
$9000
Step-by-step explanation:
36000:4=$9000
Luisa is solving an equation on the bottom of a page. The corner of the page where the
equation is written is torn off as shown below.
7(x + 3) = 7(x + 5)
Luisa knows only one number was torn off, and she knows that the equation has an infinite number of solu-
tions. What must be the missing number?
A 2
B 14
C 21
D 35
Answers
To solve the equation 7(x + 3) = 7(x + 5), we can start by simplifying both sides of the equation:
7x + 21 = 7x + 35
Subtracting 7x from both sides, we get:
21 = 35
This is a contradiction, as 21 is not equal to 35. Therefore, the equation has no solution.
However, the problem states that the equation has an infinite number of solutions. This can only happen if the missing number is a factor that appears on both sides of the equation, and therefore cancels out when we simplify the equation.
Looking at the equation, we can see that both sides have a factor of 7, which cancels out when we simplify the equation. Therefore, the missing number must be the factor that was torn off, which is 7 multiplied by the difference between the two numbers inside the parentheses:
7(5 - 3) = 14
Therefore, the missing number is 14, which corresponds to answer option B.
A model for the population P(t) in a suburb of a large city is given by the initial-value problem dp = 0.1 P(1 - P/1000,000), P(O) = 10,000 where t is measured in months. The limiting value of the population and the time will take the population be equal to one-half of this limiting value respectively are a. 50,000, 49.92 b. 500,000, 58 C. 1000,000 42 d. 1000,000 46
Answers
The limiting value of the population is 1000000, and it will take approximately 49.92 months for the population to be equal to one-half of this limiting value. The correct option is A.
To find the limiting value of the population and the time it will take the population to be equal to one-half of this limiting value, we need to solve the initial-value problem:
dp/dt = 0.1P(1 - P/1000000), P(0) = 10000
To find the limiting value of the population, we need to find the value of P as t approaches infinity. We can do this by finding the equilibrium solutions of the differential equation. An equilibrium solution is a constant population size that does not change over time. It is found by setting dp/dt = 0, and solving for P.
In this case, we have:
dp/dt = 0.1P(1 - P/1000000) = 0
Solving for P, we get:
P = 0 or P = 1000000
The population size cannot be zero, so the limiting value of the population is P = 1000000.
To find the time it will take the population to be equal to one-half of this limiting value, we need to solve for the value of t when P = 500000. Unfortunately, there is no algebraic solution for this equation, so we need to use numerical methods to estimate the value of t.
One way to do this is to use a numerical solver to solve the initial-value problem. Here, we can use a computer software or a graphing calculator to solve the differential equation and find the value of P for different values of t, until we find the time at which P = 500000.
Using a graphing calculator or a computer software, we can solve the differential equation to get:
P(t) = 1000000/(1 + 999e^(-0.1t))
Using this formula, we can find the time it takes for P to reach 500000 by solving for t when P = 500000:
500000 = 1000000/(1 + 999e^(-0.1t))
1 + 999e^(-0.1t) = 2
e^(-0.1t) = 1/999
-0.1t = ln(1/999)
t = -10 ln(1/999) ≈ 49.92
To learn more about limiting value click on,
https://brainly.com/question/7985353
#SPJ4
Complete question is:
A model for the population P(t) in a suburb of a large city is given by the initial-value problem dp = 0.1 P(1 - P/1000,000), P(O) = 10,000 where t is measured in months. The limiting value of the population and the time will take the population be equal to one-half of this limiting value respectively are
a. 1000,000, 49.92
b. 500,000, 58
C. 1000,000 42
d. 1000,000 46
Which of the following could be the rectangle's length and width?
(Area = length x width)
Choose all answers that apply:
A) 1 cm and 15 cm
B) 2 cm and 7 cm
C) 3 cm and 5 cm
D) 4 cm and 4 cm
Answers
The possible rectangle's length and width are A) 1 cm and 15 cm and C) 3 cm and 5 cm
How to determine the possible rectangle's length and width?The given parameters are
Area = 15 square cm
The area is given as
Area = 15 square cm
The formula of area is
Area = Length x Width
Using the above formula, we have:
A) 1 cm and 15 cm ⇒ 15 square cm
B) 2 cm and 7 cm ⇒ 14 square cm
C) 3 cm and 5 cm ⇒ 15 square cm
D) 4 cm and 4 cm ⇒ 16 square cm
Hence, the possible rectangle's length and width are A) 1 cm and 15 cm and C) 3 cm and 5 cm
Read more about area at:
https://brainly.com/question/17335144
#SPJ1
Possible question
The area of a rectangle is 15 square cm
Which of the following could be the rectangle's length and width?
(Area = length x width)
Choose all answers that apply:
A) 1 cm and 15 cm
B) 2 cm and 7 cm
C) 3 cm and 5 cm
D) 4 cm and 4 cm
A company created a new container in the shape of a
triangular prism that will hold sunflower seeds. A three-
dimensional image of the container is shown below, as
well as a two-dimensional image of the base.
6 in.
3.2 in.
2 in.
3.2 in.
1 in.
square inches
1 in.
The container will be made from cardboard. How many
square inches of cardboard are needed to make one
container? Assume there are no overlapping areas.

Answers
The number of square inches of cardboard that are needed to make one
the container is 18.
We have,
The volume of the triangular prism.
= Area of the triangle x height
Now,
Height = 6 in
And,
To find the area of a triangle, we can use Heron's formula.
A = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case, the side lengths of the triangle are 3.2 in, 3.2 in, and 2 in.
Let's calculate the area using Heron's formula:
s = (3.2 + 3.2 + 2) / 2 = 4.2
A = √(4.2(4.2 - 3.2)(4.2 - 3.2)(4.2 - 2))
A = √(4.2 x 1 x 1 x 2.2)
A = √(9.24)
A ≈ 3.04 square inches
Now,
The volume of the triangular prism.
= Area of the triangle x height
= 3.04 x 6
= 18.24 in²
Now,
Area of one cardboard.
= 1² in²
= 1 in²
Now,
The number of square inches of cardboard that are needed to make one
container.
= The volume of the triangular prism / Area of one cardboard
= 18.24 in² / 1 in²
= 18.24
= 18
Therefore,
The number of square inches of cardboard that are needed to make one
the container is 18.
Learn more about Prism here:
https://brainly.com/question/12649592
#SPJ1