Find the exact value of the following limit: lim x goes to 0 (e^8x-8x-1)/x^2
Answers
Answer:
32
Step-by-step explanation:
We can apple L'Hopital's Rule to solve this problem:
\(\lim _{x\to \:\:0}\left(\frac{e^{8x}-8x-1}{x^2}\right)\\=> \lim _{x\to \:0}\left(\frac{8e^{8x}-8}{2x}\right)\\\\=> \lim _{x\to \:0}\left(\frac{4\left(e^{8x}-1\right)}{x}\right)\\\\=> \lim _{x\to \:0}\left(\frac{32e^{8x}}{1}\right)\\\\=>\frac{32e^{8\cdot \:0}}{1}\\\\=> 32\)
Hope this helps!
Related Questions
María debe repartir los alimentos del convivio para elaborar los almuer-
zos de sus 22 alumnos y que cada uno reciba la misma cantidad. Tiene
kg de jamón, 3 kg de uvas, 6 litros de jugo de manzana, 25 bolillos
y 2 kg de queso. ¿Cuánto le toca a cada niño?
Answers
When Maria distribute the lunches to the 22 students equally, each person gets 1.6 of the meal.
How to calculate the value?It should be noted that from the information, Maria must distribute the lunches to the 22 students equally.
Therefore, the total foods will be:
= (3 + 6 + 25 + 2) / 22
= 36 / 22
= 1.6
Therefore each person gets 1.6 of the meal.
Learn more about expressions on:
brainly.com/question/25968875
#SPJ1
i need HELP !!!!!!!!!!!!!!!!
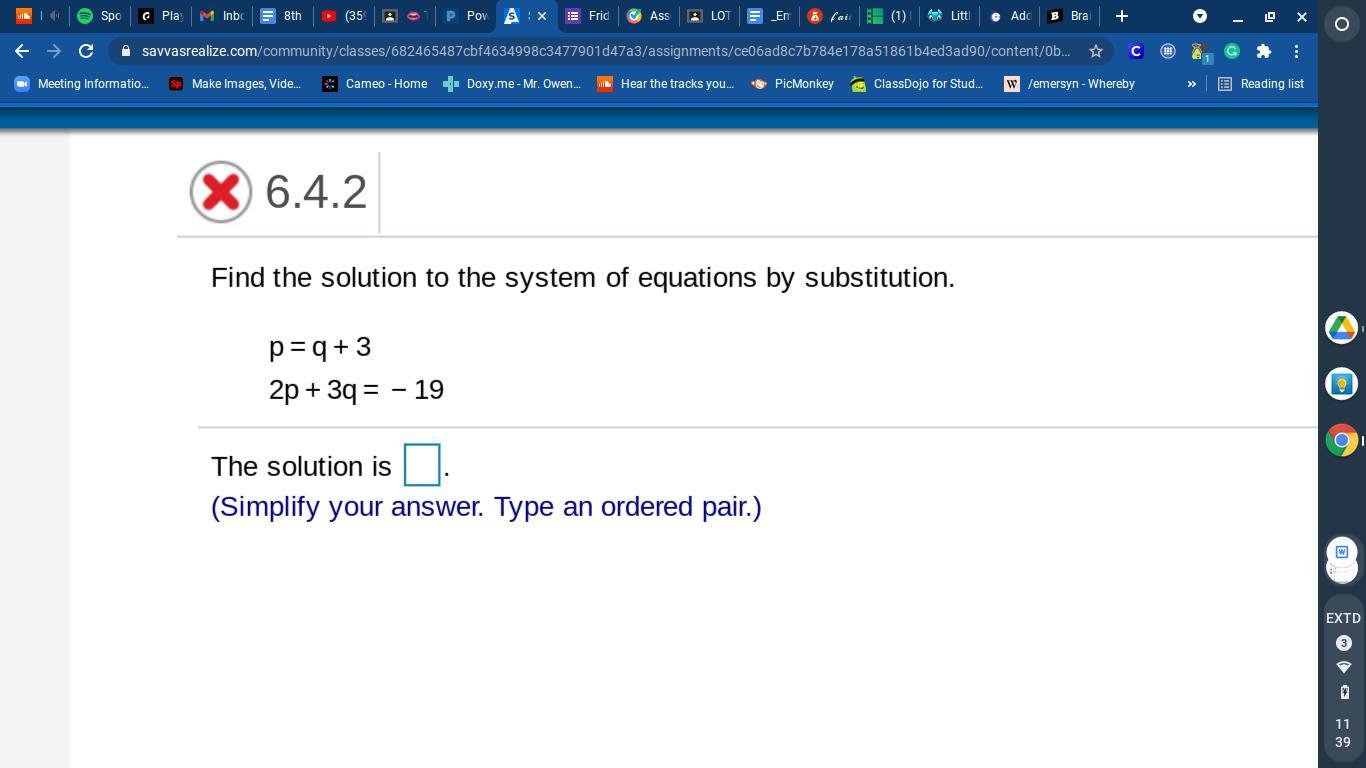
Answers
Answer:
I think the solution is (p,q)=(-2,-5)
fill in the blank. _____sample
The population is first split into groups. The overall sample consists of every member from some of the groups. The groups are selected at random.
Example—An airline company wants to survey its customers one day, so they randomly select 555 flights that day and survey every passenger on those flights.
Why it's good: A cluster sample gets every member from some of the groups, so it's good when each group reflects the population as a whole.
Answers
it is important to consider the potential for intra-cluster similarity, as individuals within the same cluster may be more similar to each other than to individuals in other clusters.
What is intra-cluster sample?A cluster sample is a sampling technique where the population is divided into clusters or groups, and a subset of clusters is selected at random to form the overall sample. In this type of sampling, all members of the selected clusters are included in the sample.
In the given example, the airline company selects 555 flights as clusters and surveys every passenger on those flights. Each flight represents a cluster, and by selecting random flights, the company includes every passenger on those selected flights in the survey.
This cluster sampling approach is suitable when each group or cluster is representative of the overall population. It is useful when it is impractical or costly to sample every individual unit within the population, but the selected clusters are expected to reflect the characteristics of the entire population.
Cluster sampling allows for more practical data collection, particularly when dealing with large populations or geographically dispersed units. However, it is important to consider the potential for intra-cluster similarity, as individuals within the same cluster may be more similar to each other than to individuals in other clusters.
Learn more about cluster sampling on:
https://brainly.com/question/15357818
#SPJ4
What is the area of the triangle? (-5,-2) (-3,5) (1.-2) 0 square units
Answers
Answer
Area = 21 Sq units
Step-by-step explanation:
Area= 1/2[(x1y2 + x2y3 + x3y1) - (x2y1 + x3y2 + x1y3)]
Area = 1/2[(-5×5 +-3×-2+1×-2) - (-3×-2+1×5+-5×-2)]
Area = 1/2(-42)
Area = -21 sq units
Area = 21 sq units (The area is negative because it is below the x-axis.)

Volume question 5 of 5 the rectangle represents the base of a right rectangular prism. the height of the prism is 6 inches. what is the volume of the prism? 13 o a. 87.9 in o b. 105.8 in 3 3 in o c. 12.6 in 2 o d. 75.6 in 3 submit
Answers
The volume of prism is 75.6 \(in^3\). The correct answer is option d,
We are given that the rectangle represents the base of a right rectangular prism and the height of the prism is 6 inches. To find the volume of the prism, we need to multiply the area of the rectangle by the height.
The area of the rectangle can be found by multiplying its length and width. However, we are not given any specific values for the length and width of the rectangle. Therefore, we cannot directly calculate its area.
Since we are given answer choices, we can use them to check which option gives the correct volume of the prism. We can start by assuming that the length, width, and height of the prism are integers, and then calculate the volume for each option until we find the one that matches.
Option a: 87.9 in^3 - This is not an integer, so we can eliminate this option.
Option b: 105.8 in^3 - This is not an integer, so we can eliminate this option.
Option c: 12.6 in^3 - This is too small, so we can eliminate this option.
Option d: 75.6 in^3 - To check if this is the correct answer, we can calculate the area of the rectangle by dividing the volume by the height.
Volume of the prism = area of rectangle x height
75.6 in^3 = (length x width) x 6 in
Length x width = 12.6 in^2
Now, we need to find two integers whose product is 12.6 in^2 and whose sum is 16 in (since the rectangle represents the base of a right rectangular prism). After some trial and error, we find that 3.15 in and 4 in satisfy these conditions.
Therefore, the length of the rectangle is 4 inches and the width is 3.15 inches.
Now, we can calculate the area of the rectangle by multiplying its length and width:
Area of rectangle = length x width = 4 in x 3.15 in = 12.6 in^2
Finally, we can calculate the volume of the prism:
Volume of prism = area of rectangle x height = 12.6 in^2 x 6 in = 75.6 in^3
Therefore, the correct answer is option d, 75.6 \(in^3\).
To learn more about Volume of prism refer here:
https://brainly.com/question/22023329
#SPJ11
The median set is 18 what is the missing number
Answers
The missing number in the median set is 6.
We are given that;
Median set=18
Now,
To find the missing number, you need to know the number of elements in the set and their order. The median is the middle value of a set when it is arranged in ascending or descending order. If the set has an odd number of elements, the median is the exact middle value. If the set has an even number of elements, the median is the average of the middle two values.
For example, if the set is {2, 4, 6, 8, 10}, the median is 6 because it is the middle value. If the set is {3, 5, 7, 9}, the median is (5 + 7) / 2 = 6 because it is the average of the middle two values.
Therefore, by median the answer will be 6.
Learn more about mean and median;
https://brainly.com/question/17060266
#SPJ1
Please help find the variable in both triangles.

Answers
Step-by-step explanation:
these are projections from V and W to the same projection "screen" (SU and YX).
since the angles are equal, the ratio between projection beam length and screen length must be the same.
so,
6.
24/14 = 48/x
48/28 = 48/x
x = 28
7.
besides the projection principle, we have a basic triangle situation :
the bisector of the angle W is also bisecting the opposing side YX. that means that this is an isoceles triangle (both legs are equally long).
therefore,
y = 4×sqrt(2)
Answer:
\(\textsf{6.} \quad x = 28\)
\(\textsf{7.} \quad y = 4\sqrt{2}\)
Step-by-step explanation:
What is an angle bisector?An angle bisector is a line that divides an angle into two equal parts.
Angle Bisector TheoremAn angle bisector in a triangle divides the opposite side into two segments which are in the same proportion as the other two sides of the triangle.
Question 6Applying the Angle Bisector Theorem:
\(\implies \dfrac{UT}{TS}=\dfrac{VU}{VS}\)
\(\implies \dfrac{x}{14}=\dfrac{48}{24}\)
Cross multiply:
\(\implies 24 \cdot x=48 \cdot 14\)
\(\implies 24x=672\)
Divide both sides by 24:
\(\implies \dfrac{24x}{24}=\dfrac{672}{24}\)
\(\implies x=28\)
Question 7Applying the Angle Bisector Theorem:
\(\implies \dfrac{XZ}{ZY}=\dfrac{WX}{WY}\)
\(\implies \dfrac{4}{4}=\dfrac{y}{4\sqrt{2}}\)
Carry out the division on the left side:
\(\implies 1=\dfrac{y}{4\sqrt{2}}\)
Multiply both sides by 4√2:
\(\implies 1\cdot 4\sqrt{2}=\dfrac{y}{4\sqrt{2}}\cdot 4\sqrt{2}\)
\(\implies 4\sqrt{2}=y\)
\(\implies y=4\sqrt{2}\)
Solve the following inequality: 38 < 4x+3+7 – 3x.
a. x < 28
b. x > 28
c. x < 4
d. x > 4
Answers
To solve the given inequality, first we have to simplify the given inequality.38 < x + 10 After simplification we get, 38 - 10 < x or 28 < x.
The correct option is B.
The given inequality is 38 < 4x + 3 + 7 - 3x. Simplify the inequality38 < x + 10 - 4x + 3 + 7 - 3x38 < -x + 20 Combine the like terms on the right side and simplify 38 + x - 20 < 0 or x + 18 < 0x < -18 + 0 or x < -18. The given inequality is 38 < 4x + 3 + 7 - 3x. To solve the given inequality, we will simplify the given inequality.
Simplify the inequality38 < x + 10 - 4x + 3 + 7 - 3x38 < -x + 20 Combine the like terms on the right side and simplify 38 + x - 20 < 0 or x + 18 < 0x < -18 + 0 or x < -18. Combine the like terms on the right side and simplify38 + x - 20 < 0 or x + 18 < 0x < -18 + 0 or x < -18.So, the answer is x > 28. In other words, 28 is less than x and x is greater than 28. Hence, the answer is x > 28.
To know more about inequality visit:
https://brainly.com/question/20383699
#SPJ11
Ella purchased a new car in 2000 for $27,600. The value of the car has been depreciating exponentially at a constant rate. If the value of the car was$8,300 in the year 2004, then what would be the predicted value of the car in the year 2009,? answer to the nearest dollar
Answers
The predicted value of the car in the year 2009 is $6,232.
How to predict the value of the car in the year 2009 ?First we need to use the formula for exponential decay:
V(t) = V0 × e^(-rt)
Where
V(t) is the value of the car at time tV0 is the initial value of the carr is the rate of decayt is the time elapsed since the initial purchaseWe know that the car was purchased in 2000 for $27,600, and that its value in 2004 was $8,300. Therefore, we can use these values to solve for the rate of decay:
$8,300 = $27,600 × e^(-r x 4)
e^(-4r) = 0.3
Taking the natural logarithm of both sides:
-4r = ln(0.3)
r = -0.3567
Now that we have the rate of decay, we can use the same formula to predict the value of the car in 2009, which is 9 years after the initial purchase:
V(9) = $27,600 × e^(-0.3567 x 9) = $6,232
Therefore, the predicted value of the car in the year 2009 is $6,232.
Learn more about exponential decay here : brainly.com/question/24077767
#SPJ1
Find a set of parametric equations for the rectangular equation that satisfies the given condition. (enter your answers as a comma-separated list. ) y = x2, t = 4 at the point (4, 16)
Answers
The set of parametric equations for the rectangular equations are x= t and y = t²
What are parametric equations?A parametric equation in mathematics specifies a set of numbers as functions of one or more independent variables known as parameters.
We have:
y = x²,
t = 4 at the point (4, 16)
The parametric equation can be model:
x = t and
y = t²
Plugging t = 4 and point (4, 16)
4 = 4 and
16 = 16
Satisfy the parametric equation.
Thus, the set of parametric equations for the rectangular equations are x= t and y = t²
Learn more about the parametric function here:
brainly.com/question/10271163
#SPJ4
Which one of these grids is shaded red and blue in the ratio 5 : 7?
A
B
D
E
F
Answers
Express in the form 1:n.
Give n as a decimal.10:12
how are intergers used to represent real world situations.
Answers
Answer:
Integers are always whole values such as 4, 10, or 58. They can represent something that can't be partial. (hope this was what you were looking for!)
2) 16 + -7
Step by step please
Answers
Answer:
9
Step-by-step explanation:
The rules that you need to know for this question are:
- & - = +
+ & - = -
+ & + = +
So for this question we have 16 + -7 so we need to use the + & - rule. Therefore a plus and a minus make a minus so we do 16-7 which is 9
Problem 4. Consider the plant with the following state-space representation. 0 *---**** _x+u; U; = y = [1 0]x
(a) Design a state feedback controller without integral control to yield a 5% overshoot and 2 sec settling time. Evaluate the steady-state error for a unit step input.
(b) Redesign the state feedback controller with integral control; evaluate the steady-state error for a unit step input. Required Steps:
(i) Obtain the gain matrix of K by means of coefficient matching method or Ackermann's formula by hand. You may validate your results with the "acker" or "place" function in MATLAB.
(ii) Use the following equation to determine the steady-state error for a unit step input, ess=1+ C(A - BK)-¹B
(iii) When ee-designing the state feedback controller with integral control, obtain the new gain matrix of K = [k₁ k₂] and ke
Answers
State feedback controllers with integral control are useful for reducing or eliminating steady-state errors in a system. The following is a step-by-step process for designing a state feedback controller with integral control:Problem 4 Consider the plant with the following state-space representation.
0⎡⎣x˙x⎤⎦=[0−4.4−20.6]⎡⎣xu⎤⎦y=[10]Part (a)To get a 5% overshoot and 2-second settling time, we design a state feedback controller without integral control. The first step is to check the controllability and observability of the system.The rank of the controllability matrix is 2, which is equal to the number of states, indicating that the system is controllable. The system is also observable since the rank of the observability matrix is 2.
The poles of the closed-loop system can now be placed using Ackermann's formula or the coefficient matching method. Ackermann's formula is used in this example. The poles are located at -5 ± 4.83i.K = acker(A,B,[-5-4.83j,-5+4.83j])The gain matrix is calculated as:K = [4.4000 10.6000]The steady-state error for a unit step input is calculated using the following equation:ess=1+ C(A - BK)-¹Bwhere C = [1 0] and D = 0. The steady-state error for a unit step input is found to be 0.Part (b)To reduce the steady-state error to zero, integral control is added to the system. The augmented system's state vector is [x xₐ]
To know more about integral visit:
https://brainly.com/question/31433890
#SPJ11
PLS HELP ASAP!! What is the solution to the equation? 98+g=150

Answers
Answer:
Its prob B im not very much sure but that the answer ill go more for because the other ones dont make sense to me
Step-by-step explanation:
Answer: g=52
Step-by-step explanation:
150-98=52
Which then G is... 52!
a racing car consumes a mean of 101 gallons of gas per race with a variance of 49 . if 43 racing cars are randomly selected, what is the probability that the sample mean would differ from the population mean by greater than 2.4 gallons? round your answer to four decimal places.
Answers
The probability that the sample mean would differ from the population mean by greater than 2.4 gallons
To solve this problem, we need to use the central limit theorem and the formula for the standard error of the mean:
Standard error of the mean = standard deviation / square root of sample size
In this case, the standard deviation is the square root of the variance, which is 7. Therefore, the standard error of the mean is:
Standard error of the mean = 7 / square root of 43 ≈ 1.061
Next, we need to calculate the z-score for a difference of 2.4 gallons:
z-score = (sample mean - population mean) / standard error of the mean
z-score = (101 - 101.6) / 1.061 ≈ -0.566
Note that we subtract the population mean from the sample mean because we want to know how much the sample mean differs from the population mean.
Finally, we can use a standard normal distribution table (or a calculator) to find the probability that a z-score is less than -0.566 or greater than 0.566 (since the distribution is symmetric). The probability of a z-sitcore less than -0.566 is approximately 0.2881, so the probability of a z-score greater than 0.566 is also approximately 0.2881. Therefore, the probability that the sample mean would differ from the population mean by greater than 2.4 gallons is:
Probability = 0.2881 + 0.2881 ≈ 0.5762
Rounding to four decimal places, the answer is 0.5762.
to learn more about probability click here -
https://brainly.com/question/13604758
#SPJ11
I don’t know how to solve these graphs. Can you please help me?

Answers
The equation of the line with slope m and y-intercept b is given by:
\(y=mx+b\)In this case the slope is 5 and the y-intercept is -2; then we have that the equation of the line is:
\(y=5x-2\)Now that we have the equation of the line we can use it to find points on the line, we do that by given values to x (whichever values we want) and use the equation to determine its corresponding y value.
If x=0, then we have:
\(\begin{gathered} y=5(0)-2 \\ y=-2 \end{gathered}\)Hence, the line passes through the point (0,-2).
If x=1, then we have:
\(\begin{gathered} y=5(1)-2 \\ y=5-2 \\ y=3 \end{gathered}\)Hence, the line passes through the point (1,3).
Now that we have two points on the line we graph them on the plane:
Finally, we join the points with a straight line. Therefore, the graph of the line is:


The question is Based on the partial set of values given for a function, identify which description best fits the function.

Answers
A) This is a linear function and the equation of the graph is conventionally y = mx + c where m is gradient and c is intercept on y axis
In this function, the equation of the graph is
y = 4x + 1
B) This is a quadratic function and it takes the form:
\(ax^2+bx+c\)where a = -1, b = 4 and c = -2. Thus the equation of this line is:
\(-x^2+4x-2\)C) This is an exponential function. The c(x) value increases with the increasing powers of 3.
What are the leading coefficient and degree of the polynomial -u^8+18+10u^3
Answers
Answer:
Step-by-step explanation:
The variable here is u, and the highest power of u is u^8. The first term is thus -u^8, and the coefficient of this is -1. Thus, the leading coefficient of the polynomial is -1. The degree is 8.
(b) what is the remainder when the following sum is divided by 4 ? $$ 1^5 2^5 3^5 \cdots 99^5 100^5 $$
Answers
The remainder when the sum \($1^5 2^5 3^5 \cdots 99^5 100^5$\) is divided by 4 is 0.
Explanation:
Any integer that is not divisible by 4 leaves a remainder of 1 when squared and a remainder of 3 when cubed.For any integer \($n$\) that is not divisible by 4, \($n^5$\) leaves a remainder of $n$ when divided by 4, because \($n^5 = (n^2)^2 \cdot n \equiv 1^2 \cdot n \equiv n \pmod{4}$\).The integers from 1 to 100 include 25 multiples of 4, so the remaining 75 integers are not divisible by 4.Thus, the remainder when \($1^5 2^5 3^5 \cdots 99^5 100^5$\) is divided by 4 is the same as the remainder when \($1^5 3^5 5^5 \cdots 99^5$\) is divided by 4.Using the reasoning above, we know that the remainder of each odd integer when raised to the fifth power is the integer itself when divided by 4.Therefore, the sum of the fifth powers of the odd integers from 1 to 99 is congruent to the sum of the integers from 1 to 99, which is divisible by 4.Adding \($100^5$\), which is clearly divisible by 4, to this sum does not change the remainder when the sum is divided by 4, so the remainder is 0.You can learn more about divisibility rule at
https://brainly.com/question/9462805
#SPJ4
The points (h,3) and ( – 2,2) fall on a line with a slope of 1/8 . What is the value of h?
Answers
Answer:
h = 6
Step-by-step explanation:
write the equation of the line in fully simplified slope-intercept form?

Answers
Answer:
y=1/5x+7
Step-by-step explanation:
i hope this helps :)
Ragan makes beaded jewelry. The graph below shows the number of beads on varying cord lengths.
Jewelry
A graph has cord length (inches) on the x-axis and number of beads on the y-axis. A line goes through points (16, 48) and (24, 72).
Which is the best estimate of the number of beads on a cord that is 16 inches long?
5
8
44
48
Answers
Answer:
48
Step-by-step explanation:
Answer:
48
Step-by-step explanation:
edge 2023
what does x equal 3.25x-2.5= -9.75x+4
Answers
Answer:
x = 6.5/13
Step-by-step explanation:
3.25x - 2.5 = -9.75x + 4
3.25x = -9.75x + 6.5
13x = 6.5
x = 6.5/13
5. A cargo plane weighed 500,000 pounds. After the first load was taken off, the airplane weighed 437,981
pounds. Then 16,478 more pounds were taken off. What was the total number of pounds of cargo
removed from the plane? Is your answer reasonable? Explain.
Answers
Answer:
A total of 78,497 pounds of cargo was removed from the plane.
Step-by-step explanation:
I got my answer by subtracting 437,981 from 500,000 to get 62,019. After, I added the additional 16,478 pounds that were taken off after to get my total of 78,497. My answer is reasonable because after double-checking with my calculator, I noticed I did not make any mistakes and my answer checked out, therefore validifying my answer. Hope this helps and have a good rest of your day/ night :)
The population of Medway, Ohio, was 4,007 in 2000. It is expected to decrease by about 0.36% per year. Write an exponential decay function and use it to approximate the population in 2020.
Answers
The population of Medway, Ohio, is expected to be approximately 3728 in the year 2020.
How to determine the exponential decay functionFrom the question, we have the following parameters that can be used in our computation:
Initial, a = 4007
Rate = 0.36% per year
The decay function is represented as
y = a(1 - rate)^x
So, we have
y = 4007 * (1 - 0.36%)^x
This gives
y = 4007 * (0.9964)^x
The year 2020 is 20 years from 2000
So, we have
x = 20
Substitute the known values in the above equation, so, we have the following representation
y = 4007 * (0.9964)^20
Evaluate
y = 3728
Hence, the approximate solution is 3728
Read more about exponential function at
https://brainly.com/question/11464095
#SPJ1
How far can she travel in 4 hours 53 minutes?

Answers
Step-by-step explanation:
1 hour she travels = 19 km
60 min = 1 hr
53 min = 1/60 * 53 hr = 53/60 hr
Now,
1 hr = 19 km
4 + 53/60 hrs = 19 * ( 4 + 53/60) km
She travels 92.78 km in 4 hrs and 53 minutes.
which two points should the line of best fit go through beer's law
Answers
For C we get
C = (A-b)/εm
Substract your y-intercept from the absorbance and divide by the slope
Beer's Law:Beer's law, or Beer-Lambert law, is a relation between the concentration, degree of attenuation, optical path length, and absorbance of a solution. This law is often employed in the analysis of chemicals as it is a straightforward relation. The law was named after August Beer and Johann Heinrich Lambert.
The basic idea here is to use a graph plotting Absorbance vs. Concentration of known solutions. Once you have that you can compare the absorbance value of an unknown sample to figure out its concentration.
You will be applying Beer's law to calculate the concentration.
The equation for Beer's law is: A = εmCl
(A=absorbance, εm = molar extinction coefficient, C = concentration, l=path length of 1 cm)
You should have a data set which was used to create a standard curve. The graph should plot concentration (independent variable) on the x-axis and absorption (dependent variable) on the y axis.
You'll need to add a line of best fit to the data points and determine the equation for the line. The equation should be in y=mx + b form.
y = absorbance (A)
Note: no unit for absorbance
x = concentration (C)
Note: unit is M or mol/L
m = (εm) = slope or the molar extinction coefficient in beers law which has units of \(M^-^1cm^-^1\)
So A = εmC +b
If you solve for C you should get
C = (A-b)/εm
So if you substract your y-intercept from the absorbance and divide by the slope, you are finding the concentration of your sample.
Learn more about Beer's law at:
https://brainly.com/question/30404288
#SPJ4
The given question is incomplete, So we take the similar question:
How do you calculate concentration from absorbance?

Rewrite the expression in the form y^n. (y^-1/2)^4

Answers
Answer:
y^ -2
Step-by-step explanation:
We know that a^b^c = a^(b*c)
(y^-1/2)^4
y^(-1/2*4)
y^ -2
Answer:
Step-by-step explanation:
Here is a data set: 1 2 3 3 4 4 4 4 5 5 6 7 What happens to the mean and standard deviation of the data set when the 7 is changed to a 70? Your answer:
Answers
When the 7 is changed to a 70, what happens is that the mean would get bigger while the standard deviation would change as well.
How to find Mean and Standard deviation?
We are given the data set as;
Data set: 1, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 7
The mean is the average of a group of data. The data set added up and divided by the number of data. The mean is sensitive to extreme data.
Standard deviation shows how much variation there is from the mean. A low SD indicates that the data points tend to be close to the mean, whereas a high SD indicates that the data are spread out over a large range of values.
When the 7 is changed to a 70, what happens is that the mean would get bigger because you are adding in a bigger number and as such the mean would increase.
The standard deviation would change as well because then again you are adding a bigger number and standard deviation is basically the difference between the greatest and least.
Read more about Mean and Standard Deviation at; https://brainly.com/question/4514629
#SPJ1