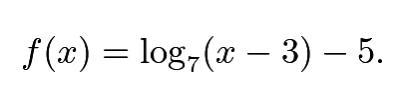Answers
The domain of the function in this problem is given as follows:
(3, ∞).
What are the domain and range of a function?The domain of a function is the set that contains all possible input values of the function, that is, all the values assumed by the independent variable x in the function.The range of a function is the set that contains all possible output values of the function, that is, all the values assumed by the dependent variable y in the function.The function in the context of this problem is given as follows:
f(x) = log7(x - 3) - 5.
The base of a logarithmic function must be positive, hence the domain of the function is obtained as follows:
x - 3 > 0
x > 3.
In interval notation, it is given as follows:
(3, ∞).
More can be learned about domain and range at https://brainly.com/question/26098895
#SPJ1
Related Questions
What is the solution of 4x^2 - 36x + 81 = 0?
Explanation please
Answers
Answer:
x=9/2
Step-by-step explanation:
find to the nearest cm the length of a shadow of a 4m flag pole when the elevation of the sun is 58°
Answers
Answer:
5cm
Step-by-step explanation:
Given
Height of the pole = 4m = opposite
Angle of elevation = 58 degrees
Required
length of shadow(hypotenuse)
Using the trig identity
Sin theta = opp/hyp
Sin 58 = 4/x
x = 4/sin58
x = 4/0.8480
x = 4.71cm
x ≈ 5cm
Hence the length of the shadow is 5cm to the nearest cm
Which of the following accurately describes the chi-square test for independence?
It is similar to a single-sample t test because it uses one sample to test a hypothesis about one population.
It is similar to a correlation because it uses one sample to evaluate the relationship between two variables.
It is similar to an independent-measures t test because it uses separate samples to evaluate the difference between separate populations.
It is similar to both a correlation and an independent-measures t test because it can be used to evaluate a relationship between variables or a difference between populations.
Answers
Option C is the correct choice as it accurately describes the chi-square test for independence. The chi-square test for independence is used to determine if there is a relationship between two categorical variables. It is similar to neither a single-sample t test nor a correlation because it involves categorical variables, not continuous ones.
Option C accurately describes the chi-square test for independence. It states that the test is similar to an independent-measures t test because it compares separate samples to evaluate the difference between separate populations.
The chi-square test for independence involves creating a contingency table that displays the observed frequencies of the two categorical variables. Then, it calculates the expected frequencies under the assumption of independence. The test compares the observed and expected frequencies using the chi-square statistic. If the observed frequencies significantly differ from the expected frequencies, we reject the null hypothesis and conclude that there is a relationship between the variables.
In contrast, options A, B, and D do not accurately describe the chi-square test for independence. Option A refers to a single-sample t test, which is not applicable to the chi-square test. Option B mentions a correlation, which assesses the relationship between continuous variables, not categorical ones. Option D combines elements of both a correlation and an independent-measures t test, which are not applicable to the chi-square test.
Therefore, option C is the correct choice as it accurately describes the chi-square test for independence.
To Know more about chi-square test for independence Visit:
https://brainly.com/question/20226847
#SPJ11
find the approximations t10, m10, and s10 for 0 8 sin(x) dx. (round your answers to six decimal places.
Answers
The correct answer is Using numerical integration techniques:Approximation using the Trapezoidal Rule (t10) is approximately [2.763211].Approximation using the Midpoint Rule (m10) is approximately [2.079728].Approximation using Simpson's Rule (s10) is approximately [2.094395].
To approximate the values of t10, m10, and s10 for the integral 0 to 8 sin(x) dx, we can use numerical integration techniques, such as the Trapezoidal Rule, Midpoint Rule, and Simpson's Rule.
Trapezoidal Rule (t10):
The Trapezoidal Rule estimates the integral by approximating the area under the curve using trapezoids. The formula for the Trapezoidal Rule is given by:
t10 = (b - a) * [(f(a) + f(b)) / 2 + ∑(f(xi))] / n
where a and b are the limits of integration (0 and 8 in this case), f(x) is the function (sin(x) in this case), xi are the equally spaced points between a and b, and n is the number of intervals.
Using n = 10, we can calculate t10:
t10 ≈ (8 - 0) * [(sin(0) + sin(8)) / 2 + ∑(sin(xi))] / 10
Midpoint Rule (m10):
The Midpoint Rule estimates the integral by approximating the area under the curve using rectangles. The formula for the Midpoint Rule is given by:
m10 = (b - a) * ∑(f(xi + h/2)) / n
where a, b, f(x), xi, and n have the same meanings as in the TrapezoidalRule, and h is the width of each interval (h = (b - a) / n).
Using n = 10, we can calculate m10:
m10 ≈ (8 - 0) * ∑(sin(xi + (8 - 0) / (2 * 10))) / 10
Simpson's Rule (s10):
Simpson's Rule estimates the integral by approximating the area using parabolic arcs. The formula for Simpson's Rule is given by:
s10 = (b - a) * [f(a) + 4 * ∑(f(xi)) + 2 * ∑(f(x2i)) + f(b)] / (3 * n)
where a, b, f(x), xi, and n have the same meanings as in the Trapezoidal Rule, and x2i represents the points with an even index.
Using n = 10, we can calculate s10:
s10 ≈ (8 - 0) * [sin(0) + 4 * ∑(sin(xi)) + 2 * ∑(sin(x2i)) + sin(8)] / (3 * 10)
By evaluating these formulas using numerical methods and rounding the results to six decimal places, you can find the approximations t10, m10, and s10 for the given integral 0 to 8 sin(x) dx.
Learn more about statistics here:
https://brainly.com/question/15525560
#SPJ11
Toni rides the Ferris wheel shown for 15 revolutions. A photo of a Ferris wheel has the diameter labeled fifty-six feet. Question 1 Part A How far does Toni travel in one revolution? Use 227 for π
Answers
Answer:
a. 176 feet b. 2640 feet
Step-by-step explanation:
a. Since the diameter of the Ferris wheel is D = 56 feet, the distance Toni travels in one revolution is the circumference of the Ferris wheel, C = πD.
So C = 22/7 × 56 ft = 22 × 8 ft = 176 feet
b. The distance traveled in 15 revolutions is thus D' = 15 × distance of one revolution = 15 × 176 = 2640 feet
Please help! will give brainlist

Answers
Answer:
1. The formula for finding the surface area of a cylinder is:
Surface Area = 2πr(r + h)
Where:
* `r` is the radius of the cylinder
* `h` is the height of the cylinder
The surface area of a cylinder is the total area of all the surfaces that make up the cylinder. This includes the two circular bases and the lateral surface. The lateral surface is the curved surface that wraps around the cylinder.
To find the surface area of a cylinder, we first need to find the area of each of the circular bases. The area of a circle is πr², where `r` is the radius of the circle. So, the area of each of the circular bases of a cylinder is πr².
We then need to find the area of the lateral surface. The lateral surface is a rectangle with height `h` and width equal to the circumference of the base. The circumference of a circle is 2πr. So, the width of the lateral surface is 2πr.
The area of a rectangle is length x width. So, the area of the lateral surface of a cylinder is 2πrh.
Adding the areas of the two circular bases and the lateral surface, we get the total surface area of the cylinder:
Surface Area = 2πr(r + h)
2. The formula for finding the surface area of a sphere is:
Surface Area = 4πr²
Where:
* `r` is the radius of the sphere
The surface area of a sphere is the total area of all the surfaces that make up the sphere. This includes the entire curved surface of the sphere.
To find the surface area of a sphere, we simply need to square the radius of the sphere and multiply it by π.
For example, if the radius of a sphere is 5 cm, the surface area of the sphere would be:
Surface Area = 4π(5 cm)² = 523.6 cm²
An emission test is being performed on n individual automobiles. Each car can be tested separately, but this is expensive. Pooling (grouping) can decrease the cost: The emission samples of k cars can be pooled and analyzed together. If the test on the pooled sample is negative, this 1 test suffices for the whole group of k cars and no more tests are needed for this group. If the test on the pooled sample is positive, then each of the k automobiles in this group must be tested separately. This strategy is referred to as a (n,k)- pooling strategy.
Suppose that we create n/k disjoint groups of k automobiles (assume n is divisible by k) and use the pooling method. Assume the probability that a car tests positive is p, and that each of the n individuals autos are "independent," i.e., their tests are independent of one another.
Finally suppose that the cost for testing an emission sample is C, no matter how many individual elements are pooled in the sample.
a. Given a pooled sample of k autos, what is the expected cost to test the sample so that results are known for each individual auto?
b. Compute the testing cost per car for n = 1000, p = 0.02, k = 10, C = $100.00
c. Compute the testing cost per car for n = 1000, p = 0.02, k = 5, C = $100.00
Answers
The expected cost per pooled sample is: (1 - p)^k * C + (1 - (1 - p)^k) * (C + C * k) , the testing cost per car is $28.30 for n = 1000, p = 0.02, k = 10, and C = $100.00 and the testing cost per car is $29.70.
a. Expected cost to test a pooled sample of k autos:
If the test on the pooled sample is negative, we only incur the cost of testing one sample, which is C.
If the test on the pooled sample is positive, we need to test each car separately, which incurs an additional cost of C for each car.
The probability that a pooled sample tests negative is (1 - p)^k, and the probability that it tests positive is 1 - (1 - p)^k.
Therefore, the expected cost per pooled sample is: (1 - p)^k * C + (1 - (1 - p)^k) * (C + C * k).
b. For n = 1000, p = 0.02, k = 10, and C = $100.00:
In this case, the number of pooled samples, m, is given by n/k = 1000/10 = 100.
The total expected cost can be calculated by multiplying the expected cost per pooled sample by the number of pooled samples:
Total expected cost = m * expected cost per pooled sample
Cost per car = Total expected cost / n
Substitute the given values into the formula:
m = 100
p = 0.02
k = 10
C = $100.00
Calculate the expected cost per pooled sample:
Expected cost per pooled sample = (1 - 0.02)^10 * $100.00 + (1 - (1 - 0.02)^10) * ($100.00 + $100.00 * 10)
= 0.817 * $100.00 + 0.183 * $1100.00
= $81.70 + $201.30
= $283.00
Calculate the total expected cost:
Total expected cost = 100 * $283.00
= $28,300.00
Calculate the cost per car:
Cost per car = $28,300.00 / 1000
= $28.30
Therefore, the testing cost per car is $28.30 for n = 1000, p = 0.02, k = 10, and C = $100.00.
c. For n = 1000, p = 0.02, k = 5, and C = $100.00:
Similar to part b, calculate the expected cost per pooled sample, total expected cost, and cost per car using the given values:
m = 1000/5 = 200
p = 0.02
k = 5
C = $100.00
Calculate the expected cost per pooled sample:
Expected cost per pooled sample = (1 - 0.02)^5 * $100.00 + (1 - (1 - 0.02)^5) * ($100.00 + $100.00 * 5)
= 0.903 * $100.00 + 0.097 * $600.00
= $90.30 + $58.20
= $148.50
Calculate the total expected cost:
Total expected cost = 200 * $148.50
= $29,700.00
Calculate the cost per car:
Cost per car = $29,700.00 / 1000
= $29.70
Therefore, the testing cost per car is $29.70.
Therefore, the expected cost per pooled sample is: (1 - p)^k * C + (1 - (1 - p)^k) * (C + C * k) , the testing cost per car is $28.30 for n = 1000, p = 0.02, k = 10, and C = $100.00 and the testing cost per car is $29.70.
To know more about cost check the below link:
https://brainly.com/question/28147009
#SPJ4
rotation 90° clockwise about the origin

Answers
Answer:
point s at (0,5) point t at (5,3) point u at (4,1)
Step-by-step explanation:
happy life
The figure shown has two parallel lines cut by a transversal:
A pair of parallel lines is shown, crossed by a transversal. Angles are identified as 1, 2, 3, 4, 5, 6, 7, and 8. Angles 1-4 are on the top line clockwise from upper left. Angles 5-8 are on the lower line clockwise from upper left.
Use the figure to complete the sentence. (4 points)
∠3 and ____ are alternate interior angles.
a
∠2
b
∠6
c
∠5
d
∠8
Answers
The Answer is C and I am 100% sure about it
Answer:c
Step-by-step explanation:
I took the test
Which one is the correct answer please I need help!

Answers
Answer:
B
Step-by-step explanation:
perform the operation and reduce the answer fully 2/3 / 7/8
Answers
Answer:
0.762
Step-by-step explanation:
2/3 / 7/8 = 2*8 / 7*3 = 16/21 = 0.762
Direction: Explain each study described in each scenario. (Sample Surveys Study, Experiment Study or Observational Study).
1. Engineers are interested in comparing the mean hydrogen production rates per day for three different heliostat sizes. From the past week's records, the engineers obtained the amount of hydrogen produced per day for each of the three heliostat sizes. That they computed and compared the sample means, which showed that the mean production rate per day increased with heliostat sizes..
a. Identify the type of study described here.
b. Discuss the types of interference that can and cannot be drawn from this study.
Answers
The study described in this scenario is an experiment study. The engineers are interested in comparing the mean hydrogen production rates per day for three different heliostat sizes.
They collect data from the past week's records and compute and compare the sample means to determine if the mean production rate per day increases with heliostat sizes.
(a) The study described here is an experiment study. In an experiment, researchers manipulate or control the variables of interest to determine their effects. In this case, the engineers are comparing the mean hydrogen production rates for different heliostat sizes by collecting data and computing sample means. They have control over the sizes of the heliostats and can measure the resulting hydrogen production rates.
(b) From this study, the engineers can draw conclusions about the relationship between heliostat size and mean hydrogen production rates. By comparing the sample means, they observe that the mean production rate per day increases with heliostat sizes. However, there are certain limitations and inferences that cannot be made from this study alone.
For example, the study does not provide information about the causal relationship between heliostat size and hydrogen production rates. Other factors, such as environmental conditions or operational parameters, may also influence the production rates. Additionally, the study does not account for potential confounding variables or address any potential biases in the data collection process. Further research or additional experimental designs may be necessary to establish a stronger causal relationship and generalize the findings.
Learn more about production here: brainly.com/question/30333196
#SPJ11
the dotplot above shows the distribution of calf measurements for 507 adults who attend a local gym. the data is divided into equal-sized subgroups with 25% of the adults in each subgroup. which measure of center can you most accurately estimate from this information?
Answers
which measure of center can you most accurately estimate from this information: Median
The median divides the data into equal-sized groups. So approximately 50% of the data is above the median and approximately 50% of the data is below the median.
Calculating the median
The median is the value in a data set, implying that half of data focuses have a value more modest or equivalent to the median and half of data focuses have a value higher or equivalent to the median.
For a little data set, you first count the quantity of data focuses (n) and organize the data focuses in expanding request. Assuming the quantity of data focuses is lopsided, you add 1 to the quantity of places and separation the outcomes by 2 to get the rank of the data point whose value is the median.
The rank is the place of the data point after the data set has been organized in expanding request: the smallest value is rank 1, the second-smallest value is rank 2, and so forth.
to know more about median click here:
https://brainly.com/question/16408033
#SPJ4
the complete question is:
The dotplot above shows the distribution of calf measurements for 507 adults who attend a local gym. The data is divided into equal-sized subgroups with 25% of the adults in each subgroup.
Which measure of center can you most accurately estimate from this information?
1. mean
2. median
When we use the term ideal fluid, we neglect: O density O pressure O energy conservation O friction and we assume laminar flow
Answers
When using the term ideal fluid, the assumption of neglecting friction is made. Frictional forces are not considered in ideal fluid analysis, while other factors such as density, pressure, energy conservation, and laminar flow are still accounted for.
An ideal fluid is a theoretical concept used in fluid mechanics to simplify the analysis of fluid flow. When considering an ideal fluid, certain assumptions are made to simplify the equations and calculations involved. These assumptions include neglecting friction.
Friction is the resistance encountered by a fluid when it flows over a surface or through a pipe. In real-world scenarios, frictional forces play a significant role in fluid flow, causing energy losses and affecting the behavior of the fluid. However, when dealing with ideal fluids, friction is ignored to simplify the analysis.
Other options listed in the question:
- Density: In ideal fluid analysis, density is not neglected. The density of the fluid is still considered and can affect the calculations.
- Pressure: In ideal fluid analysis, pressure is also considered and plays a role in determining the fluid behavior.
- Energy conservation: Energy conservation is still a fundamental principle in fluid mechanics, even when dealing with ideal fluids. It is not neglected.
- Laminar flow: The assumption of laminar flow is often made when analyzing ideal fluids. Laminar flow refers to smooth, orderly flow without turbulence. It is one of the simplifying assumptions used in ideal fluid analysis.
Learn more about friction visit:
https://brainly.com/question/24338873
#SPJ11
In a football stadium, 43% of the crowd cheering for Team A, and 52% of the crowd is female. 19% of the crowd is cheering for Team A and female . What is the probability that a randomly selected Person from the crowd are cheering for Team A or female?
Answers
P(Female) = 0,52
P(TeamA and Female) = 0,19
P(TeamA or Female) = ?
P(TeamA or Female) = P(TeamA) + P(Female) - P(TeamA and Female) <=>
P(TeamA or Female) = 0,43 + 0,52 - 0,19 <=>
P(TeamA or Female) = 0,76 or 76%
please help
will mark brainliest

Answers
For two consecutive natural numbers m and n, where m<n, it is known that n - m = 1 (for example, 5 and 6 are consecutive and 6 - 5 = 1). In this case, if the largest number is x, then the previous number is x - 1, and the previous for x - 1 is x - 2.
Other two numbers in terms of x are x - 1; x - 2.
Answer:
(x - 1) and (x - 2)
Step-by-step explanation:
Consecutive natural numbers are a sequence of natural numbers that follow each other in order without any gaps or interruptions. Natural numbers are positive integers starting from 1 and continuing indefinitely. Therefore, consecutive natural numbers begin with 1 and increment by one unit for each subsequent number in the sequence.
If "x" is the largest of 3 consecutive natural numbers, then the natural number that comes before it will be 1 unit smaller than x, so:
x - 1The natural number that comes before "x - 1" will be 1 unit smaller than "x - 1", so:
x - 1 - 1 = x - 2Therefore, if x is the largest of 3 consecutive natural numbers, the other 2 numbers in terms of x are x - 1 and x - 2.
Let A = {1, 2, 3, 4, 5}, B = {0, 3, 6}, and C = {2, 4, 6, 7}.
Find
(a) A ∪ B
(b) A ∩ B
(c) A − B
(d) B − A
(e) C ∪ (B − A)
(f) (C ∪ B) − A
Answers
To find the union of two sets, we combine all the elements in both sets, without duplicating any elements. (a) A ∪ B = {0, 1, 2, 3, 4, 5, 6} (b) A ∩ B = {3} (c) A − B = {1, 2, 4, 5} (d) B − A = {0, 6} (e) C ∪ (B − A) = {0, 2, 3, 4, 6, 7} (f) (C ∪ B) − A = {0, 6, 7}
To find the intersection of two sets, we find the elements that are common to both sets. A − B = {1, 2, 4, 5}
To find the set difference A − B, we remove all the elements in B from A. B − A = {0, 6} To find the set difference B − A, we remove all the elements in A from B. C ∪ (B − A) = {0, 2, 3, 4, 6, 7} First, we find the set difference B − A, which is {0, 6}.
Then, we find the union of C and {0, 6}, which is {0, 2, 4, 6, 7}. (C ∪ B) − A = {0, 6, 7} First, we find the union of C and B, which is {0, 2, 3, 4, 6, 7}. Then, we remove all the elements in A from this set to get the result.
Know more about union here:
https://brainly.com/question/29055360
#SPJ11
What are the measures of angles b and d? ∠b = 55°; ∠d = 55° ∠b = 55°; ∠d = 125° ∠b = 97°; ∠d = 97° ∠b = 83°; ∠d = 97°
Answers
In parallelogram ABCD, ∠b = 55°; ∠d = 55. So, the correct answer is (a).
We know that opposite angles of a parallelogram are congruent. In another words, opposite angles of parallelogram are equal. Therefore, we equate the angle B and angle D to each other and solve.
angle B = angle D
2n + 15 = 3n - 15
n = 30
The value of n is 30.
Now we can find the measures of angles B and D:
angle B = 2n + 15 = 2(30) + 15 = 75 degrees
angle D = 3n - 15 = 3(30) - 15 = 75 degrees
Therefore, the answer is (a) ∠b = 55°; ∠d = 55
To know more about parallelogram :
https://brainly.com/question/16578666
#SPJ4
____The given question is incomplete, the complete question is given below:
In parallelogram ABCD measure of angle b is 2n+15 and angle d is 3n - 15. What are the measures of angles b and d? a)∠b = 55°; ∠d = 55° b) ∠b = 55°; ∠d = 125° c) ∠b = 97°; ∠d = 97° d)∠b = 83°; ∠d = 97°
Answer:
The Answer is A
Step-by-step explanation:
I just took the test! 2023Edg
solve for m - hp = d for p
please actually help this is my first assignment of the year and can’t fail
Answers
m - hp = d
-hp = d - m.
Then, all we have to do is isolate the “p” variable:
p = -(d - m) / h
p = ( -d + m ) / h
anaiah is currently consuming 20 eggplants and 30 kiwis. his marginal utility per dollar spent on the 20th eggplant is 160 utils and his marginal utility per dollar spent on the 30th kiwi is 190 utils. the price of an eggplant is $3 and the price of a kiwi is also $3. he has $180 to spend.
How much is Anaiah currently spending on these goods?
What are the reasons that Anaiah is behaving irrationaly?
- he is not spending his entire income
- he is spending to much on kiwis
- he is not balancing what he spends.on each good
- his marginal utility per dollar spent is not the same for both goods
Answers
Anaiah currently spending $150 on these goods
*He is not spending his entire income
*His marginal utility per dollar spent is not the same for both goods
What is unit rate?
A unit rate is the cost for only one of anything. This is expressed as a ratio with a denominator of 1. For instance, if you covered 70 yards in 10 seconds, you did so at an average speed of 7 yards per second. Although both of the ratios—70 yards in 10 seconds and 7 yards in one second—are rates, only the latter is a unit rate.
consumption of eggplant
= 20 price of eggplant
= 3
consumption of kiwi is
= 30 price of eggplant
= 3
Formula:
Spending
= price of eggplant*consumption of eggplant + price of kiwi*consumption of kiwi
= 3*20+3*30
= 150
Utility per one dollar spent on the 20th eggplant
= 160
Marginal utility per dollar spent on the 30th kiwi
= 190 utils.
Note that y 160<190
Currently spending= 150
& budget = 180
150<180
According theory of choice consumer need the maximize the utility so answer is
Answer -:
*He is not spending his entire income
*His marginal utility per dollar spent is not the same for both goods
To learn more about the unit rate from the given link
https://brainly.com/question/4895463
#SPJ1
evaluate the integral. (remember to use absolute values where appropriate. use c for the constant of integration.) x2 − x 36 x3 6x dx
Answers
The value of the given integral is \((-1/18)ln|x| - (1/36)ln|6x^2-1|\)+ C, where C is the constant of integration.
To evaluate the integral, we can use integration by substitution. Let u = x² - x, then \(\frac{du}{dx}\) = 2x - 1 and dx = \(\frac{du}{(2x-1)}\). Substituting this in the integral, we get:
∫ \((x^2 - x)/(36x^3 - 6x)\)dx = ∫ \(\frac{u}{18x(2x-1)} du\)We can further simplify this by breaking the integral into partial fractions:
\(\frac{u}{(18x(2x-1))}\) = A/x + B/(2x-1)
u = A(2x-1) + Bx
Equating coefficients, we get A = -1/18 and B = 1/18. Substituting these values, we get:
∫ \(\frac{(x^2 - x)}{(36x^3 - 6x)}\) dx = (-1/18)∫ \(\frac{dx}{x}\) + (1/18)∫ dx/(2x-1)
= \((-1/18)ln|x|\) - (1/36)ln|2x-1| + C
Since the natural logarithm function is only defined for positive values, we need to use absolute values in the final answer to account for negative values of x. Therefore, the answer is
\((-1/18)ln|x| - (1/36)ln|6x^2-1|\) + C.
Learn more about Integrals:
https://brainly.com/question/22008756
#SPJ4
Cooling towers are used to remove or expel heat from a process. A cooling tower's walls are modeled by x squared over 400 minus quantity y minus 110 end quantity squared over 2304 equals 1 comma where the measurements are in meters. What is the width of the cooling tower at the base of the structure? round your answer to the nearest whole number.
Answers
The width of the cooling tower at the base of the structure as calculated from the data is 40 meters.
The equation which is given is ,
x²/400 -(y-90)²/1600=1
To calculate the width,
Cooling tower width =2√400
=2×20
=40 meters
Therefore the width is 40 meters.
A cooling tower is a type of heat removal device which uses water to remove waste heat from a process and discharge it into the atmosphere.
Similarly, an industrial cooling tower works by removing heat from water by evaporating little percentage of the water that is recirculated through the unit. When warm water and cooler air mingle, the latent heat of vaporization is released, causing the water to cool.
To learn more about width
brainly.com/question/25855344
#SPJ4
The width of the cooling tower at the base of the structure is 16 meters.
x = 16 meters
x^2/400 - (y - 110)^2/2304 = 1
x^2/400 = (y - 110)^2/2304 + 1
400x^2 = 2304(y - 110)^2 + 2304
400x^2 = 2304y^2 - 514240y + 2574304
x^2 = 514240y/400 - 2574304/400 = 514.6y - 6435.76
x = √(514.6y - 6435.76)
For y = 0, x = 16 meters
Therefore, the width of the cooling tower at the base of the structure is 16 meters (rounded to the nearest whole number).The width of the cooling tower at the base of the structure is 16 meters.
learn more about width here
brainly.com/question/25855344
#SPJ4
a two-dimensional form that occupies an area is called a(n)
Answers
A two-dimensional form that occupies an area is called a shape.
Shapes can be various types such as rectangles, circles, triangles, and many others, and they are defined by their properties such as sides, angles, and vertices. They are defined by their boundaries or edges and exist within a plane. These forms have dimensions of length and width, but not depth. Shapes play a fundamental role in geometry and are studied extensively in mathematics and art. They can be simple or complex, symmetrical or asymmetrical, and are used to represent objects, patterns, or designs. Whether in the natural world or man-made creations, shapes are integral to our understanding and appreciation of visual compositions.
To know more about symmetrical, visit:
https://brainly.com/question/31184447
#SPJ11
suppose x is normally distributed with mean 5 and standard deviation 4 find each of the following probablties
Answers
If x is normally distributed with mean 5 and standard deviation 4, the probabilities are
a) P(X < 3) = 0.3085.
b) P(X > 8) = 0.2266.
c) P(1 < X < 9) = 0.6826.
We need to use the standard normal distribution to solve these problems, so we will first standardize the variable x.
Let Z be the standard normal random variable, then
Z = (X - μ) / σ
where μ = 5 and σ = 4.
a) P(X < 3)
Standardizing, we have
Z = (3 - 5) / 4 = -0.5
Using a standard normal table or calculator, we find that P(Z < -0.5) = 0.3085.
Therefore, probabilities of P(X < 3) = 0.3085.
b) P(X > 8)
Standardizing, we have
Z = (8 - 5) / 4 = 0.75
Using a standard normal table or calculator, we find that P(Z > 0.75) = 0.2266.
Therefore, P(X > 8) = 0.2266.
c) P(1 < X < 9)
Standardizing, we have
Z1 = (1 - 5) / 4 = -1
Z2 = (9 - 5) / 4 = 1
Using a standard normal table or calculator, we find that P(Z < -1) = 0.1587 and P(Z < 1) = 0.8413.
Therefore, P(1 < X < 9) = P(-1 < Z < 1) = P(Z < 1) - P(Z < -1) = 0.8413 - 0.1587 = 0.6826.
Your question is incomplete but most probably your full question was
Suppose x is normally distributed with mean 5 and standard deviation 4 find each of the following probabilities
a) P(X < 3)
b) P(X > 8)
c) P(1 < X < 9)
Learn more about probability at https://brainly.com/question/28088905
#SPJ11
Brian is an 8th grade student and wants to attend UCLA when he graduates high
school. He plans on getting a part time job in high school so he can start saving for
college. Which of the following options would allow Brian to save the most money?
A
Start saving money as a Senior in high school by adding $150 a month to his
savings account.
B
Start saving money as a Freshman in high school by adding $100 a month to an
account that compounds annually at 5%.
Start saving money as a Sophomore in high school by adding $100 a month to an
account that eams 3% simple interest.
Start saving money as a Junior in high school in a shoe box under his bed
whenever he remembers to add money to it.
Answers
Answer: Option B would allow Brian to save the most money.
If he starts saving as a freshman and adds $100 a month to an account that compounds annually at 5%, he would have four years of savings before starting college. Using the formula for compound interest:
A = P(1 + r/n)^(nt)
where A is the amount of money accumulated, P is the principal (the initial amount of money), r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time (in years).
If Brian starts with $0 and adds $100 a month for four years (48 months), he would have a total of $4,800. If this money is compounded annually at 5%, the formula becomes:
A = 4800(1 + 0.05/1)^(1*4) = $5,907.15
Therefore, by saving $100 a month in an account that compounds annually at 5%, Brian would accumulate $5,907.15 by the time he starts college, which is more than the other options provided.
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
The size of our lecture hall, Hasbrouck 20 , is about 9 m across. What is the minimum amount of light energy that can exist in Hasbrouck 20? If you think that an arbitrarily small amount of light can exist (you could keep dividing the brightness forever) enter zero. Answers either in Joules (J) or eV will be accepted as correct. To enter a value using scientific notation, use "E" and be sure to sign your exponent. For example, the mass of the electron would be written 9.11E-31 and Avogadro's Number would be written 6.022E+23.
Answers
The minimum number amount of light energy that can exist in Hasbrouck 20 is zero due to the divisibility of light.
According to quantum theory, light is composed of particles called photons. Each photon carries a certain amount of energy, which is directly proportional to its frequency.
However, the size of the lecture hall being 9 m across does not impose any constraints on the minimum amount of light energy. In the quantum realm, light can be continuously divided, and there is no lower limit to the amount of light energy that can exist.
Therefore, the minimum amount of light energy in Hasbrouck 20 is considered to be zero.
This implies that arbitrarily small quantities of light can exist, and the division of light energy can continue indefinitely.
Learn more about Number click here :brainly.com/question/3589540
#SPJ11
A tank contains 60 kg of salt and 1000 L of water. Pure water enters a tank at the rate 6 L/min. The solution is mixed and drains from the tank at the rate 3 L/min. (a) What is the amount of salt in the tank initially? (b) Find the amount of salt in the tank after 4.5 hours. (c) Find the concentration of salt in the solution in the tank as time approaches infinity. (Assume your tank is large enough to hold all the solution.)
Answers
Initially, the tank contains 60 kg of salt, calculated by multiplying the salt concentration (0.06 kg/L) by the water volume (1000 L).
In the given scenario, the tank starts with a known salt concentration and water volume. By multiplying the concentration (0.06 kg/L) with the water volume (1000 L), we find that the initial amount of salt in the tank is 60 kg.
After 4.5 hours, considering the rate of water entering and leaving the tank, the net increase in solution volume is 810 L. Multiplying this by the initial concentration (0.06 kg/L), we determine that the amount of salt in the tank after 4.5 hours is 48.6 kg.
As time approaches infinity, with a constant inflow and outflow of solution, the concentration of salt in the tank stabilizes at the initial concentration of 0.06 kg/L.
Learn more about Multiplying click here :brainly.com/question/25834626
#SPJ11
5. HELP FAST If each person paid an equal amount, who would save the most money? Explain your reasoning using at least two complete sentences
Answers
Person A would save the most money because they had a coupon that was worth more than their portion of the purchase price.
To determine who would save the most money if each person paid an equal amount, we need to calculate how much each person paid and then compare the amounts saved by each person. For instance, let's consider an example with four people who want to split the cost of a $60 purchase equally. Each person would pay $60 / 4 = $15.
If person A has a $20 coupon, then they would save $20, and their net cost would be $15 - $20 = -$5. Person B has a $15 coupon, so they would save $15, and their net cost would be $15 - $15 = $0. Person C has a $10 coupon, so they would save $10, and their net cost would be $15 - $10 = $5. Person D has a $5 coupon, so they would save $5, and their net cost would be $15 - $5 = $10.
You can learn more about coupons at: brainly.com/question/31727353
#SPJ11
Which option is it?

Answers
Answer:
Yes, because the products of means is equal to the product of extreme
Step-by-step explanation:
(9 x 10^6) + (8 x 10^{-4})