Answers
Answer:
(-4/3,2]
Step-by-step explanation:
Remember the bracket that I placed
Related Questions
6sin^2 (x) + 6sin (x) + 1 = 0
solve and show steps for the graph ( i already have the graph )
Answers
To solve the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0, we can use algebraic methods and the unit circle to determine the values of x that satisfy the equation.
1. Start by rearranging the equation to a quadratic form: \(6sin^2(x)\) + 6sin(x) + 1 = 0.
2. Notice that the equation resembles a quadratic equation in terms of sin(x). Let's substitute sin(x) with a variable, such as u: \(6u^2\) + 6u + 1 = 0.
3. Solve this quadratic equation for u. You can use the quadratic formula or factorization methods to find the values of u. The solutions are u = (-3 ± √3) / 6.
4. Since sin(x) = u, substitute back the values of u into sin(x) to obtain the values for sin(x): sin(x) = (-3 ± √3) / 6.
5. To find the values of x, we can use the inverse sine function. Take the inverse sine of both sides: x = arcsin[(-3 ± √3) / 6].
6. The arcsin function has a range of [-π/2, π/2], so the values of x lie within that range. Use a calculator to find the approximate values of x based on the values obtained in step 5.
7. Plot the obtained x-values on the graph to show the solutions of the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0. The graph will illustrate the points where the curve intersects the x-axis.
For more such questions on algebraic, click on:
https://brainly.com/question/4344214
#SPJ8
Please help.
Answer question 1 and 2 and I’ll mark brainliest
1. You and your friends are making favors for
a party. You make a profit of half a dollar
per favor. How many must you sell to make
a profit of $250? Write an equation and
solve.
2. North High School has 762 students. This
is three times the number of students at
Central High. How many students does
Central High have? Write an equation
and solve.
publishing as Pearson Prentice Hall.
Answers
Answer:
1. 500
2. 2,286
Step-by-step explanation:
1. $250 divide by 0.5
2. 762 times by 3
At a concert for the band Algal Rhythms, 75% of the tickets were sold at the full price of $30. The remaining 25% of tickets were sold at a discounted price of $10. What was the average selling price of a ticket at the Algal Rhythms concert? Express your answer in dollars, rounded to the nearest cent.
Answers
The average selling price of a ticket at the Algal Rhythms concert is $25
How to determine the average selling price of a ticket at the Algal Rhythms concert?The given parameters are:
75% of the tickets were sold for $30.
The remaining 25% were sold for $10.
The average selling price of a ticket at the Algal Rhythms concert is calculated using
Average = Sum of (Price * Percentage)
So, we have
Average = 30 * 75% + 10 * 25%
Evaluate the expression
Average = 25
Hence, the average selling price of a ticket at the Algal Rhythms concert is $25
Read more about average at:
https://brainly.com/question/20118982
#SPJ1
what is an equation of the tangent line at x = 2, assuming that y(2) = 4 and y'(2) = 5?
Answers
Therefore, the equation of the tangent line at x = 2 is y = 5x - 6.
The equation of the tangent line at x = 2 can be found using the point-slope formula: y - y1 = m(x - x1), where (x1, y1) is the given point on the curve and m is the slope of the tangent line at that point.
In this case, we are given that y(2) = 4 and y'(2) = 5. This means that the point on the curve at x = 2 is (2, 4) and the slope of the tangent line at that point is 5.
Using the point-slope formula, we can plug in these values and simplify:
y - 4 = 5(x - 2)
y - 4 = 5x - 10
y = 5x - 6
Therefore, the equation of the tangent line at x = 2 is y = 5x - 6.
To know more about tangent line visit:-
https://brainly.com/question/31326507
#SPJ11
Prove or disprove Prove or disprove Prove or disprove Prove or disprove : For any integer a, 14 | (33 — 5) or 21 i
(2a+ 3) . : There exists an integer a such that 14 | (33 — 5) or 21 | (2a + 3) : There exist odd integers a and b
such that 4 i (3a2 + b2). : For all odd integers a and b, 4| (3532 + b2).
Answers
For any integer a, 14 does not divide (33 - 5) or 21 does not divide (2a + 3).
There exists an integer a such that 14 divides (33 - 5) or 21 divides (2a + 3).
There exist odd integers a and b such that 4 does not divide (3a^2 + b^2).
For all odd integers a and b, 4 does not divide (353^2 + b^2).
To prove or disprove the statement "For any integer a, 14 | (33 - 5) or 21 | (2a + 3)", we can evaluate the expressions for different values of a. Let's try a = 1 and a = 2:
For a = 1:
(33 - 5) = 28 and
(2a + 3) = 5. Neither 14 divides 28 nor 21 divides 5.
For a = 2:
(33 - 5) = 28 and
(2a + 3) = 7. Neither 14 divides 28 nor 21 divides 7.
From these examples, we can see that the statement is false. For any integer a, neither 14 divides (33 - 5) nor 21 divides (2a + 3).
To prove or disprove the statement "There exists an integer a such that 14 | (33 - 5) or 21 | (2a + 3)", we can again evaluate the expressions for different values of a. Let's try a = 4:
For a = 4:
(33 - 5) = 28 and
(2a + 3) = 11. Neither 14 divides 28 nor 21 divides 11.
From this example, we can conclude that the statement is false. There does not exist an integer a such that 14 divides (33 - 5) or 21 divides (2a + 3).
To prove or disprove the statement "There exist odd integers a and b such that 4 | (3a^2 + b^2)", we can try different combinations of odd integers for a and b and check if 4 divides (3a^2 + b^2). Let's try a = 1 and b = 1:
For a = 1 and
b = 1:
(3a^2 + b^2) = (3 * 1^2 + 1^2) = 4. In this case, 4 divides (3a^2 + b^2).
Therefore, we have found an example where 4 divides (3a^2 + b^2) for odd integers a and b. The statement is true.
To prove or disprove the statement "For all odd integers a and b, 4 | (353^2 + b^2)", we can again try different combinations of odd integers for a and b and check if 4 divides (353^2 + b^2). Let's try a = 1 and b = 1:
For a = 1 and
b = 1:
(353^2 + b^2) = (353^2 + 1^2). In this case, 4 does not divide (353^2 + 1^2).
Therefore, we have found a counterexample where 4 does not divide (353^2 + b^2) for odd integers a and b. The statement is false.
For any integer a, 14 does not divide (33 - 5) or 21 does not divide (2a + 3).
There does not exist an integer a such that 14 divides (33 - 5) or 21 divides (2a + 3).
There exist odd integers a and b such that 4 divides (3a^2 + b^2).
For all odd integers a and b, 4 does not divide (353^2 + b^2).
To know more about odd integers, visit
https://brainly.com/question/490943
#SPJ11
Write "four hundred dollars and seventy-two cents" as a decimal
Answers
Answer:
$400.72
Step-by-step explanation:
Please help me solve this problem please and thank you

Answers
Answer:
y = 0
x = 8
Step-by-step explanation:
subtract second equation from first one
3x - 6y - (3x - y) = 24 - 24 the - sign in front of the parenthesis effects the inside expressions
3x - 6y - 3x + y = 24 - 24 add/subtract like terms
-5y = 0 and so y = 0
to find the value of x we can use this information
3x - y = 24 since y = 0
3x = 24 divide both sides by 3
x = 8
a. For the following function, find f'(a). b. Determine an equation of the line tangent to the graph of fat (a.f(a)) for the given value of a. f(x)=√2x+4, a=6 a. f'(a) =
Answers
a. For the following function, find f'(a). The function is
f(x) = √(2x + 4).f'(x) = 1/2(2x + 4)-1/2*2
f'(6) = 1/4
b. Determine an equation of the line tangent to the graph of fat (a.f(a)) for the given value of a.
f(x) at x = a.
y = 1/4x - 3/2 is the equation of the tangent line to the graph of f(a) at x = 6.
a. For the following function, find f'(a). The function is
f(x)
= √(2x + 4).f'(x)
= 1/2(2x + 4)-1/2*2
The above function can be simplified as:
f'(x)
= 1/(√2x + 4)
Now we have to find f'(a) where a
= 6
Substituting the value of x with a in the above function we get:
f'(6)
= 1/(√2*6 + 4)
f'(6)
= 1/(√16)
f'(6)
= 1/4
b. Determine an equation of the line tangent to the graph of fat (a.f(a)) for the given value of a.
We have to find the equation of the tangent line of the function
f(x) at x
= a.
To find the equation of the tangent line we have to use the point-slope form of the line which is:
y - y1
= m(x - x1)
where m is the slope of the tangent line and (x1, y1) is the point at which the line is tangent to the curve.
f(x)
= √(2x + 4)f(a)
= √(2a + 4)
f'(x)
= 1/(√2x + 4)
f'(a)
= 1/(√2a + 4)
At x
= a,
the point is (a, f(a)) and the slope of the tangent line is f'(a).
Therefore, the equation of the tangent line is:
y - f(a)
= f'(a)(x - a)
Substituting the value of f(a), f'(a) and a in the above equation we get:
y - √(2*6 + 4)
= 1/(√2*6 + 4)(x - 6)
y - √16 = 1/4(x - 6)y - 4
= 1/4(x - 6)
y
= 1/4x - 3/2
is the equation of the tangent line to the graph of f(a) at x
= 6.
To know more about line tangent visit:
https://brainly.com/question/23416900
#SPJ11
Which number is greater than 10?

Answers
Answer:
C.
Step-by-step explanation:
The square root of five is greater than two - the square root of four is two, so it kind of has to be bigger.
Five times two is ten.
Since the square root of five is larger than two, five times the square root of five must be bigger.
Answer:
I used calc to figure it out but its C
2.Here is a histogram that summarizes the lengths, in feet, of a group of adult femalesharks. Highlight all the statements that are true, according to the histogram.1086420 13 13.51414.515 15.5 16 16.517 17.5length in feet
Answers
We are given a histogram that summarizes the lengths, in feet, of a group of adult female sharks.
Let us analyze each of the given options.
Option A: A total of 9 sharks were measured.
This seems to be incorrect since the number of sharks is way more than that.
Option B: A total of 50 sharks were measured.
Let us count the exact number of sharks from the histogram.
0 to 13 = 0
13 to 13.5 = 1
13.5 to 14 = 1
14 to 14.5 = 4
14.5 to 15 = 10
15 to 15.5 = 10
15.5 to 16 = 9
16 to 16.5 = 10
16.5 to 17 = 4
17 to 17.5 = 1
So, the total number of sharks is
1 + 1 + 4 + 10 + 10 + 9 + 10 + 4 + 1 = 50
Therefore, the statement B is correct.
Option C: The longest shark that was measured was 10 feet long.
As you can see from the histogram, the longest length that was measured is 17 to 17.5 feet.
Therefore, this statement is incorrect.
Option D: Most of the sharks that were measured were over 16 feet long.
As you can see from the histogram, the peaks of the histogram lie in the range of 14.5 to 16.5 feet.
This means that the majority of the sharks that were measured are between 14.5 to 16.5 feet.
Therefore, this statement is incorrect.
Option E: Two of the sharks that mere measured were less than 14 feet long.
As you can see from the histogram, there are two sharks having lengths less than 14 feet long.
13 to 13.5 = 1
13.5 to 14 = 1
Therefore, this statement E is correct.
from 1980 to 1990, the consumer price index
Answers
Answer:
1.51
Step-by-step explanation:
If it wrong i'm sorry
Find the exact value of sin 105º.
Answers
Answer:
sin 105 = sin (45 + 60) = sin 45 cos 60 + cos 45 sin 60, or
= (1 / √2)(1 / 2) + (1 / √2)(√3 / 2)
1 + √3
= -------------
2√2
Step-by-step explanation:
(according to my calculator)
i need the answer asap lol..

Answers
Answer:
144
Step-by-step explanation:
sense you have the line in the triangle you would add that to the 16 (length) and multiply that by the 6 (hight) and that would be the area (144)
find x
(6x+24)° (10x)°

Answers
Answer:
The answer is 6
Step-by-step explanation:
10x-6x=24
4x=24
x=24/4
x=6
The price of three apples at quick market is $1.44 the price of the home of the same apples at Walmart is $2.50 which place is the better buy
Answers
Answer:
Quick market is better.
Step-by-step explanation:
3 apples = $1.44
Walmart 5 apples = $2.50
quick market 1 apple = $1.44/3
quick market = $0.48
Walmart 1 apple = $2.50/5
Walmart = $0.5
Evaluate the expression using a calculator. Round your answer to two decimal places when appropriate.
Square root 5^32,768 =

Answers
The value of the equation is A = ⁵√32,768 is A = 8
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Substituting the values in the equation , we get
A = ⁵√32,768 be equation (1)
On simplifying the equation , we get
A = 8 x 8 x 8 x 8 x 8 = 32,768
So , the 5th root of ( 32,768 ) is 8
Therefore , the value of A = 8
Hence , the equation is A = 8
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
These four lines have been graphed on the same line. Which lines are parallel to each other?

Answers
Answer:
C. J and I
Step-by-step explanation:

-2y - 5y = 9 Solve by elimination
3x+11y=4
Answers
x= -17
y=5
——-
I had this question on a quiz and got it right
Write the equation in slope-intercept form. y = 6(x + 2) + 5x
Answers
Answer:
y=11x+12
Step-by-step explanation:
y = 6(x + 2) + 5x
y=6x+12+5x
y=11x+12
in slope interception form= y=mx+c
y=11x+12
what is the range of f?

Answers
Answer:
[-4,5]
Step-by-step explanation:
you look on the starting point and the ending point of the y-axis ( you always start with the smallest value)
What two consecutive integers does 20−−√ fall between?
Answers
Answer:
4 and 5
Step-by-step explanation:
If 20% of x is equal to x-20, what is the value of x?
Answers
well, first off, what's 20% of "x" anyway?
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{20\% of x}}{\left( \cfrac{20}{100} \right)x}\implies \cfrac{20x}{100}\implies \cfrac{x}{5} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{x}{5}~~ = ~~x-20\implies x=5x-100\implies x+100=5x \\\\\\ 100=4x\implies \cfrac{100}{4}=x\implies \boxed{20=x}\)
What outcome is likely to occur for a hypothesis test evaluating a treatment that has a very large and robust effect?
Answers
For the given statement, we have to correctly rejecting the null hypothesis.
According to the statement
we have to find the outcome when hypothesis test evaluating a treatment that has a very large and robust effect.
For this purpose, we know that the
A hypothesis is a testable statement about the relationship between two or more variables or a proposed explanation for some observed phenomenon.
And according to the given statement it is clear that the by this we have to rejected this hypothesis.
because this treatment and the large effects are not possible for the independent values of the hypothesis.
In other words, we can say that the we have to correctly rejecting the null hypothesis.
So, For the given statement, we have to correctly rejecting the null hypothesis.
Learn more about hypothesis here
https://brainly.com/question/11555274
#SPJ4
a frequency distribution in which high scores are most frequent (i.e. bars on the graph are highest on the right hand side) is said to be:
Answers
A frequency distribution in which high scores are most frequent is said to be positively skewed or right-skewed.
In statistics, skewness refers to the asymmetry of a probability distribution. A frequency distribution is said to be positively skewed or right-skewed if the majority of the data is concentrated on the right side of the distribution, while a few high values are outliers on the right tail. The frequency distribution will look like a graph that is shifted to the right with a longer tail on the right side.
Positive skewness means that the mean (average) of the data will be higher than the median (middle value). The median is a more robust measure of central tendency than the mean in a positively skewed distribution, because it is not influenced by the outliers on the right tail.
To know more on skewness
https://brainly.com/question/30038569
#SPJ4
Solve 3x² 12x +15= 0 by completing the square.
-
The solutions are x =
and x =
Answers
The required solutions are x = 1 and x = -5
Given is the quadratic equation 3x²+ 12x - 15= 0
Here the first step is to first multiply the first term that is a and the last term c
the given quadratic expression can be generalized as ax² + bx + c = 0
So first multiply 3 and 15 and the product which we will get is 45.
And then try to express this product as the sum of two numbers such that these two numbers difference would be the number which is in the middle that is the alphabet b
So 45 is the product of 15 and 3
and the difference of these two number 15-3 = 12
Thus these are the required numbers
thus we can simply write it as
3x² + 15x - 3x - 15 = 0
3x ( x + 5 ) - 3 ( x + 5 ) = 0
( 3x - 3 ) ( x +5 ) = 0
thus the values of x are
3x - 3 =0
3x = 3 and this implies x = 1
and from the second expression x + 5 = 0
this implies x = -5
To know more about quadratic expressions you may visit the link which is mentioned below:
https://brainly.com/question/1863222
#SPJ13
PLEASE HELP! John rolled a ball between 25 1/4ft, and 25 3/4ft. of the choices below roll could be John's?
25.2
25.5
25.8
25
Answers
Answer:
25.5
Step-by-step explanation:
convert the question fractions to numbers with decimal points...
the ball rolled between 25 1/4 or 25.25 feet,
and 25 3/4 or 25.75 feet.
so the answer must be 25.5.
the other 3 answers are eitger kess than, or more than the distance his ball rolled.
a sphere is filled with air. if the volume of the sphere is increasing at a rate of 569 cubic inches per minute, what is the rate, in inches per minute, at which the radius of the sphere is changing when the radius is 4 inches? submit an exact answer. remember that the volume of a sphere is v
Answers
The rate, in inches per minute, at which the radius of the sphere is changing when the radius is 4 inches is 2.83
What is the Volume of a Sphere?
The capacity of a sphere is its volume. It is the area that the sphere occupies. Cubic measurements of a sphere's volume include m3, cm3, in3, etc. The sphere has a circular, three-dimensional form. Its form is determined by three axes: the x, y, and z axes. Sports like basketball and football are all instances of spheres with volume.
Since the cross-section of the sphere is a circle, the volume in this case is dependent on the diameter of the sphere's radius. The area or region of a sphere's outer surface is known as its surface area. We may use the following formula to get the volume of a sphere whose radius is "r":
Here, In the question, It is given that:
Radius = 4inch.
Rate of increase = 569 cubic inches;
So, using the Volume of Sphere, formula:
\(\begin{aligned}v=\frac{4}{3} \pi r^3 \\\frac{d v}{d t} &=\frac{d}{d t}\left[\frac{4}{3} \pi r^3\right] \\&=\frac{4 \pi}{3}\left(3 r^2\right) \frac{d r}{d t} \\\frac{d v}{d t} &=4 \pi r^2 \frac{d r}{d t}\end{aligned}\)
\(\begin{aligned}&\frac{d r}{d t}=\frac{\frac{d v}{d t}}{4 \pi r^2}\\&\left.\frac{d r}{d t}=\frac{569}{(4 \pi)(4)^2}=\frac{d}{d t}_{r=4}^{d r^2}=569\right]\\&\frac{d v}{d t}=\frac{569}{64 \pi} \sim 2.83\end{aligned}\)
Hence, the rate, in inches per minute, at which the radius of the sphere is changing when the radius is 4 inches is 2.83
To learn more about Sphere, visit:
https://brainly.com/question/1122024
#SPJ4
Can someone answer this for me? I haven’t done geometry in a while so I need a refresher.
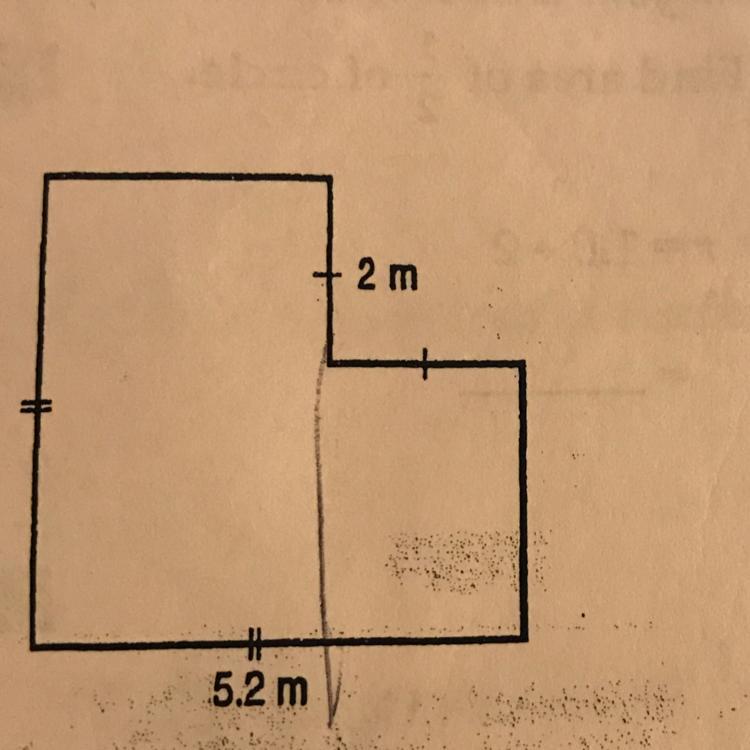
Answers
I believe I have to calculate the area of the shape. I'll do that.
Answer:
Total area = 23.04 square m
Step-by-step explanation:
Area of a compound shape
The shape shown in the figure can be divided into two smaller rectangles. We need to find their dimensions.
The single tick in the 2 m side indicates the other side also measures 2 m. This means the width of one of the smaller rectangles is 5.2m - 2 m = 3.2 m
The double tick in the 5.2 m also indicates the length of that smaller rectangle is 5.2 m. Thus the two rectangles have their respective areas as:
A1 = 5.2 m * 3.2 m = 16.64 square m
A2 = 2 m * 3.2 m = 6.4 square m
The total area is:
At = 16.64 square m + 6.4 square m = 23.04 square m
Total area = 23.04 square m
Using the standard normal distribution, find each probability.
P(0 < z < 2.16)
P(−1.87 < z < 0)
P(−1.63 < z < 2.17)
P(1.72 < z < 1.98)
P(−2.17 < z < 0.71)
P(z > 1.77)
P(z < −2.37)
P(z > −1.73)
P(z < 2.03)
P(z > −1.02)
Answers
Answer: The probabilities are:
P(0 < z < 2.16) = 0.4832
P(−1.87 < z < 0) = 0.4681
Step-by-step explanation:
1- P(0 < z < 2.16)
Using a standard normal distribution table, we can get that the probability of z being between 0 and 2.16 is 0.4832.
2- P(−1.87 < z < 0)
Using a standard normal distribution table, we can find that the probability of z being between -1.87 and 0 is 0.4681.
3- P(−1.63 < z < 2.17)
Using a standard normal distribution table, we can find that the probability of z being between -1.63 and 2.17 is 0.8587.
4-P(1.72 < z < 1.98)
Using a standard normal distribution table, we can find that the probability of z being between 1.72 and 1.98 is 0.0792.
5- P(−2.17 < z < 0.71)
Using a standard normal distribution table, we can find that the probability of z being between -2.17 and 0.71 is 0.4435.
6- P(z > 1.77)
Using a standard normal distribution table, we can find that the probability of z being less than or equal to 1.77 is 0.9616. However, we want the probability of z being greater than 1.77, so we use the complement rule: P(z > 1.77) = 1 - P(z ≤ 1.77) = 1 - 0.9616 = 0.0384.
7- P(z < −2.37)
Using a standard normal distribution table, we can find that the probability of z being less than or equal to -2.37 is 0.0083.
8- P(z > −1.73)
Using a standard normal distribution table, we can find that the probability of z being less than or equal to -1.73 is 0.0418. However, we want the probability of z being greater than -1.73, so we use the complement rule: P(z > -1.73) = 1 - P(z ≤ -1.73) = 1 - 0.0418 = 0.9582.
10- P(z < 2.03)
Using a standard normal distribution table, we can find that the probability of z being less than or equal to 2.03 is 0.9798.
11- P(z > −1.02)
Using a standard normal distribution table, we can find that the probability of z being less than or equal to -1.02 is 0.1543. However, we want the probability of z being greater than -1.02, so we use the complement rule: P(z > -1.02) = 1 - P(z ≤ -1.02) = 1 - 0.1543 = 0.8457.
Learn more about probability here, https://brainly.com/question/25839839
#SPJ11
a cone-shaped container has a height of 9 inches and diameter of 2.5 inches. it is filled with a liquid that is worth $2 per cubic inch. what is the total value of the liquid in the container?
Answers
The total value of the liquid in the cone-shaped container is $244.09.
To find the total value of the liquid in the container, we first need to calculate the volume of the cone. The formula for the volume of a cone is V = (1/3) * π * r^2 * h, where r is the radius and h is the height. Given that the diameter is 2.5 inches, the radius (r) is half of the diameter, which is 1.25 inches. Plugging in the values, we get V = (1/3) * 3.14 * 1.25^2 * 9 = 35.04 cubic inches.
Since the liquid is worth $2 per cubic inch, we can calculate the total value by multiplying the volume by the price per cubic inch: $2 * 35.04 = $70.08. Therefore, the total value of the liquid in the cone-shaped container is $70.08.
Learn more about volume : brainly.com/question/28058531
#SPJ11
