Answers
Related Questions
Find the value of x and show all steps please

Answers
Answer:
\(x=3\)
Step-by-step explanation:
\((x)(4x)=(4)(9)\)\(\frac{4x^2}{4} =\frac{36}{4}\)\(\sqrt{x^2}=\sqrt{9}\)\(x=3\)---------------------
hope it helps...
\( \implies \sf{(x)(4x) = (4) \: (9)}\)
\( \implies \sf{ \frac{4 {x}^{2} }{4} } = \frac{36}{4} \)
\( \implies \sf{ \sqrt{ {x}^{2} } = \sqrt{9} }\)
\( \sf \boxed {x = 3}\)
________________________Thank you
Hope it helps uh :)
Wich equation shows ax - w = 3 solved for w
Answers
Answer:
Answer depends on the value you put
Step-by-step explanation:
let's say a= 3 and x =4 then,
or 3*4 -w = 3
or 12 - w = 3
or -w = 3- 12
or -w = -9
or w = 9
just put any value in a and x and you will get the answer
Use distributive property to rewrite each algebraic expression: 8(s + 5)
Answers
Answer:
8s + 40
Step-by-step explanation:
8*s = 8s
8*s = 40
8s + 40
Answer: The correct answer is 8s+40
Step-by-step explanation: If it's correct can i get brainliest..... hopes this helps.
What is the height of the cylinder? The figure is not drawn to scale.
V = 282.7 in²
18 in
11.3 in
7.2 in
3.6 in

Answers
The height of the cylinder is \(3 inch\)
How can the height of the cylinder be found?Based on the attached figure,
Volume of the cylinder = 282.7 square inches
Radius of the cylinder =5 inches.
The height of the cylinder = ?
The volume of the cylinder can be found with the formula as :
\(V=pi r^{2} h\)
\(h=\frac{V}{pi r^{2} } \\\\h = \frac{282.7}{3.142 * 5^{2} } \\\\=3 inch\)
Learn more about cylinder at:
https://brainly.com/question/9554871
#SPJ1
let a be a finite non-empty set. does there exist a relation r on a that is both an equivalence relation and an order relation?
Answers
The required relation on R on A is explain below
What is finite non-empty set?It is a set where either the quantity of components is large or just beginning or finishing is given. In this way, we mean it with the quantity of components, n(A), and on the off chance that n(A) is a characteristic number, it's a limited set.
According to question:Let A be finite non-empty set.
Then the exist relation R on A which is both equivalence and order relation.
Suppose A = {a₁, a₂, a₃........an}
And, R = {(a₁, a₁)(a₂, a₂).......}
R not equal to ∅ and it is reflexive, symmetric, transitive, anti symmetric.
Then R is equivalence relation and an order relation.
To know more about sets visit:
brainly.com/question/28860949
#SPJ4
A random sample of 150 teachers in an inner-city school district found that 72% of them had volunteered time to a local charitable cause within the past 12 months. What is the standard error of the sample proportion?
a. 0.037
B. 0.057
C. 0.069
D. 0.016
Answers
The given information is as follows:A random sample of 150 teachers in an inner-city school district found that 72% of them had volunteered time to a local charitable cause within the past 12 months.
The formula for calculating the standard error of sample proportion is given as:$$Standard\(\ error=\frac{\sqrt{pq}}{n}$$\)where:p = proportion of success in the sampleq = proportion of failure in the samplen = sample sizeGiven:Sample proportion, p = 72% or 0.72Sample size, n = 150
The proportion of failure in the sample can be calculated as:q = 1 - p= 1 - 0.72= 0.28Substituting the known values in the above formula, we get:\($$Standard \ error=\frac{\sqrt{pq}}{n}$$$$=\frac{\sqrt{0.72(0.28)}}{150}$$$$=0.0372$$\)Rounding off to the nearest thousandth, we get the standard error of sample proportion as 0.037
To know more about values visit:
https://brainly.com/question/30145972
#SPJ11
Fill in the missing volumes in the table to create equivalent ratios

Answers
Answer: The answer is 12 and 20 should be 10
what is the value of x in 12 ( x + 10 ) = 24
also explain
Answers
Answer: x = -8
Step-by-step explanation:
12 ( x + 10 ) = 24
First we divide the two sides of the exercise by 12.
\(\boldsymbol{\sf{x+10=\dfrac{24}{12} }}\)
We divide 24 by 12..
x + 10 = 2
Subtract 10 from both sides.
x = 2 - 10
Subtract 10 from 2 to get. Since the number 10 is greater than 2, the result will be negative.
x = -8
Answer:
\( \sf \: x = - 8\)
Step-by-step explanation:
Given equation,
→ 12(x + 10) = 24
Now the value of x will be,
→ 12(x + 10) = 24
→ 12(x) + 12(10) = 24
→ 12x + 120 = 24
→ 12x = 24 - 120
→ 12x = -96
→ x = -96 ÷ 12
→ [ x = -8 ]
Hence, the value of x is -8.
PART 1 Please help me 10 points i just joined today ;)
PART 2 is on other question





Answers
Answer:
B=30,000
Y=The Plane's altitude
M= -2,000
X= Minutes
Equation: y=-2,000x+30,000
Slope= ?
Y-intercept= the point where you start at
what is the altitude after 10 minutes?=10,000
How Long does it take to get to 0 altitudes?=15 (Minutes)
Step-by-step explanation:
What are the choices for slope
Triangles A and B are similar. The side lengths of Triangle A in inches are 4.5, 7.0, and 5.25. The corresponding lengths in inches for Triangle B are 13.5, 21.0, and x. Solve for x.
Answers
Answer:
The value of x is 15.75
Explanation:
Given that triangles A and B are similar.
Side lengths of triangle A are: 4.5, 7.0, and 5.25
Side lengths of triangle B are: 13.5, 21.0, and x
Since the triangles are similar, the following ratios are correct:
13.5/4.5 = 21/7 = x/5.25
3 = x/5.25
Multiply both sides of the equation by 5.25
x = 15.75
Solve the compound inequality 2x – 3 < 7 and 5 – x ≤ 8.
Answers
Answer:
[-3,5)
Step-by-step explanation:
Compound inequality
2x - 3 < 7
And
5 - x ≤ 8
The solution is the conjunction of the individual solutions because both conditions must be met.
From the first inequality we get:
2x < 7 + 3
2x < 10
x < 5
From the second inequality we get:
- x ≤ 8 - 5
- x ≤ 3
Multiplying by -1 and flipping the sign:
x ≥ -3
Thus the solution is the set of numbers that lie in the interval [-3,5)
Scrapper Elevator Company has 20 sales representatives who sell its product throughout the United States and Canada. The number of units sold last month by each representative is listed below. Assume these sales figures to be the population values. 2 3 2 3 3 4 2 4 3 2 2 7 3 4 5 3 3 3 3 5 Required: a. Compute the population mean. (Round your answer to 1 decimal place.) b. Compute the standard deviation. (Round your answer to 2 decimal places.) c. If you were able to list all possible samples of size five from this population of 20, how would the sample means be distributed
Answers
Using the concepts of mean and standard deviation, and the central limit theorem, it is found that:
a. The mean is of: 3.3
b. The standard deviation is of: 1.23.
c. They would have a mean of 3.3 and a standard deviation of 0.55.
What are the mean and the standard deviation of a data-set?The mean of a data-set is given by the sum of all values in the data-set, divided by the number of values.The standard deviation of a data-set is given by the square root of the sum of the differences squared between each observation and the mean, divided by the number of values.For this problem, the mean is given by:
M = (2 + 3 + 2 + 3 + 3 + 4 + 2 + 4 + 3 + 2 + 2 + 7 + 3 + 4 + 5 + 3 + 3 + 3 + 3 + 5)/20 = 3.3
The standard deviation is:
\(S = \sqrt{\frac{(2 - 3.3)^2 + (3 - 3.3)^2 + \cdots + (3 - 3.3)^2 + (5 - 3.3)^2}{20}} = 1.23\)
What does the Central Limit Theorem states?It states that for distribution of sample means of size n:
The mean remains constant.The standard deviation is of S/sqrt(n).Hence, since 1.23/sqrt(5) = 0.55, the sample means would have a mean of 3.3 and a standard deviation of 0.55.
More can be learned about the standard deviation of a data-set at https://brainly.com/question/24754716
#SPJ1
What is the range of the function graphed below?
A. -2
B. -∞
C. -∞
D. -∞

Answers
Mr. Greene is trying to decide which charter bus
company to use for the 8th grade Outer Banks trip.
Holiday Tours charges a down payment of $300 and $3
per mile. Diamond Tours charges a $500 down payment
and $1 per mile. Write and solve an equation to find the
number of miles when the cost of both companies will be
the same.
Answers
Answer: 100 miles
Step-by-step explanation:
300+3x=500+1x
subtract 1 from both sides
300+2x=500
subtract 300 from both sides
2x=200
divide 2
x=100
Choose the CORRECT conversion factor.
O 1 cm=.01 mm
1000ml = 1 liter
O 1cm = 100m
0 1 km
1000ml

Answers
Answer:
1000 mL = 1 L
Step-by-step explanation:
This is how you convert mL to L
A polygon is regular when all angles are equal and all sides are equal
True or False
Answers
Answer:
True
Step-by-step explanation:
True, because a polygon have all angles that are equal and all lengths are the same length.
Write the sentence as an equation.
292 decreased by p is the same as 27
Type a slash (/)if you want to use a division sign.
Answers
I’m not sure if this is what you meant
the probability that a certain radioactive mass emits no particles in a one-minute time period is 0.1352. what is the mean number of particles emitted per minute?
Answers
The mean number of particles emitted per minute is approximately 2.0026.
To find the mean number of particles emitted per minute, we can use the Poisson distribution formula for the probability of no particles being emitted in a one-minute time period, which is given by:
\(P(X=0) = e^(-λ) × (λ^0) / 0! = 0.1352\)
where λ is the mean number of particles emitted per minute, e is the base of the natural logarithm (approximately 2.718), and X is the number of particles emitted.
Step 1: Rearrange the formula to solve for λ:
\(e^(-λ) = 0.1352\)
Step 2: Take the natural logarithm of both sides:
\(-ln(λ) = ln(0.1352)\)
Step 3: Solve for λ:
λ = -ln(0.1352)
Step 4: Calculate the value:
λ ≈ 2.0026
The mean number of particles emitted per minute is approximately 2.0026.
for such more question on mean
https://brainly.com/question/1136789
#SPJ11
Given the function f(x)=cosh(x). a) Find the first four non-zero terms of the Maclaurin series for f(x). b) Write the power series using summation notation. c) Determine the interval of convergence of the series.
Answers
Given function is f(x) = cosh(x).We need to find the first four non-zero terms of the Maclaurin series for f(x), write the power series using summation notation and determine the interval of convergence of the series.
Part (a)We need to find the Maclaurin series for f(x), and for that, we first need to find its derivatives with respect to x.
f(x) = cosh(x)
f'(x) = sinh(x)
f''(x) = cosh(x)
f'''(x) = sinh(x)
f''''(x) = cosh(x)
The Maclaurin series of f(x) is given by
f(x) = f(0) + f'(0)x + (f''(0)/2!) x² + (f'''(0)/3!) x³ + .....
Substituting the values of f(0), f'(0), f''(0), f'''(0) and f''''(0) in the above equation,
we get
f(x) = 1 + x²/2! + x⁴/4! + x⁶/6! + .....= Σn=0 to ∞ \([(x^(2n))/(2n)!],\) where n = 0, 1, 2, ....
The first four non-zero terms of the Maclaurin series for f(x) are:1, x²/2!, x⁴/4!, x⁶/6!
Part (b)Writing the power series using summation notation, we get:
f(x) =\(Σn=0 to ∞ [(x^(2n))/(2n)!]\), where n = 0, 1, 2, ....
Part (c)To find the interval of convergence, we use the ratio test.
The ratio test states that if Σa_n is a series, then the series is convergent if lim n→∞ \((a_(n+1)/a_n)\) < 1, and is divergent if lim n→∞ \((a_(n+1)/a_n)\) > 1, and is inconclusive if lim n→∞ \((a_(n+1)/a_n)\) = 1.
Here, \(a_n = x^(2n)/(2n)!\)
∴\(a_(n+1) = x^{(2(n+1))}/(2(n+1))!\)
Therefore,
\(lim n→∞ (a_(n+1)/a_n) = lim n→∞ [(x^(2(n+1))/(2(n+1))!)/ (x^(2n)/(2n)!)]\)
∴\(lim n→∞ (a_(n+1)/a_n) = lim n→∞ (x²/(2(n+1))(2n+1))= 0\)
Thus, the series converges for all values of x.
Now we can summarize the answer below
a) The first four non-zero terms of the Maclaurin series for f(x) are: 1, x²/2!, x⁴/4!, x⁶/6!.
b) Writing the power series using summation notation, we get: f(x) = Σn=0 to ∞\([(x^(2n))/(2n)!],\) where n = 0, 1, 2, ....
c) The series converges for all values of x.
The interval of convergence of the given series is (-∞, ∞).
To know more about derivatives visit:
brainly.com/question/25324584
#SPJ11
A critical? value, z Subscript alphaz??, denotes the? _______.
a. area to the left of z = ??
b. z-score with an area of ?? to its right.
c. z-score with an area of ?? to its left.
d. area to the right of z=??
Answers
A critical value, z Subscript alphas is (c) z-score with an area of ?? to its left.
A critical value, denoted as z (Subscript α/2), is a point on the standard normal distribution curve, which is used in hypothesis testing. It helps to determine whether to accept or reject the null hypothesis. In this context, the critical value denotes the z-score with an area of ?? to its left, which represents the probability of observing a value more extreme than the critical value in the left tail of the distribution.
The critical value z Subscript α/2 signifies the z-score with an area of ?? to its left on the standard normal distribution curve, which is crucial for hypothesis testing.
To know more about probability, visit:
https://brainly.com/question/30034780
#SPJ11
[14] Prove that n2+1 > 2" when n is a positive integer. [8] [15] Repeat previous question using strong induction with 15 ns4. [4]
Answers
1. The inequality n^2 + 1 > 2^n holds true for all positive integers n.
2. Using strong induction with 15 as the base case, we can prove that n^2 + 1 > 2^n for all positive integers up to 15.
3. The proof relies on the assumption that if the inequality holds for n and all previous values up to 15, it also holds for n+1.
To prove that n^2 + 1 > 2^n for all positive integers n, we can use mathematical induction. In the base case, we need to show that the inequality holds true for n = 1. Substituting n = 1 into the inequality, we get 1^2 + 1 > 2^1, which simplifies to 2 > 2, which is true.
Now, we assume that the inequality holds for some positive integer k, where k ≥ 1. In other words, we assume k^2 + 1 > 2^k. We need to prove that the inequality also holds for k + 1, i.e., (k + 1)^2 + 1 > 2^(k + 1). Expanding and simplifying the left side of the inequality, we get k^2 + 2k + 2 > 2^k * 2.
Since we assumed k^2 + 1 > 2^k, we can rewrite the left side as (k^2 + 1) + 2k + 1 > 2^k + 2. Now, we can use the inductive hypothesis and the fact that k ≥ 1 to say that (k^2 + 1) + 2k + 1 > 2^k + 2. Therefore, we have shown that if the inequality holds for k, it also holds for k + 1.Since the inequality is true for the base case of n = 1, and we have shown that if it holds for any positive integer k, it also holds for k + 1, we can conclude that the inequality n^2 + 1 > 2^n is true for all positive integers n.
To learn more about integers click here brainly.com/question/30719820
#SPJ11
Describe in words a sequence of transformations that maps △ABC to △A^' B^' C^'.
Write an ordered-pair rule for this sequence of transformations.

Answers
If sequence of transformations that maps △ABC to △A^' B^' C^'.The sequence of transformation is 90 degrees counterclockwise rotation, followed by a vertical translation to the right by 2 unit. The ordered pair-rule for each are (x,y) tends to (-x,-y)
What is Transformation ?A transformation is a general term for four specific ways to manipulate the shape and/or position of a point, a line, or geometric figure.
Image is the original shape of the object and final shape ond position of the object is the preimage.
In the given figure,
original image is △ABC and △A^' B^' C^' is the preimage.
Transformation includes changing the position of a shape.
The steps followed for transformation include rotating the image to 90 degrees counterclockwise rotation, later by a vertical translation to the right by 2 unit.
The ordered pair-rule for each are (x,y) tends to (-x,-y)
Hence △ABC is the original image and △A^' B^' C^' is the preimage and The ordered pair-rule for each are (x,y) tends to (-x,-y)
To learn more on Transformations click:
https://brainly.com/question/11709244
#SPJ1
10. Prove that if f is uniformly continuous on I CR then f is continuous on I. Is the converse always true?
Answers
F is continuous at every point x₀ ∈ I. Thus, f is continuous on an interval I.
Regarding the converse, the statement "if f is continuous on an interval I, then it is uniformly continuous on I" is not always true. There exist functions that are continuous on a closed interval but not uniformly continuous on that interval. A classic example is the function f(x) = x² on the interval [0, ∞). This function is continuous on the interval but not uniformly continuous.
To prove that if a function f is uniformly continuous on interval I, then it is continuous on I, we need to show that for any ε > 0, there exists a δ > 0 such that for any x, y ∈ I, if |x - y| < δ, then |f(x) - f(y)| < ε.
Since f is uniformly continuous on I, for the given ε, there exists a δ > 0 such that for any x, y ∈ I, if |x - y| < δ, then |f(x) - f(y)| < ε.
Now, let's consider an arbitrary point x₀ ∈ I and let ε > 0 be given. Since f is uniformly continuous, there exists a δ > 0 such that for any x, y ∈ I, if |x - y| < δ, then |f(x) - f(y)| < ε.
Now, choose δ' = δ/2. For any y ∈ I such that |x₀ - y| < δ', we have |f(x₀) - f(y)| < ε.
Therefore, for any x₀ ∈ I and ε > 0, we can find a δ' > 0 such that for any y ∈ I, if |x₀ - y| < δ', then |f(x₀) - f(y)| < ε.
This shows that f is continuous at every point x₀ ∈ I. Thus, f is continuous on interval I.
Learn more about arbitrary point:
https://brainly.com/question/19195471
#SPJ11
please help im not good at math its worth 51 points

Answers
Answer:
11 : 4
Step-by-step explanation:
Hey there!
To find the ratio of something, we have to use this symbol --> :
The correct format of a ratio is x : y
In this case, they are asking round-up (x) to slingshot (y)
Using the graph we can find the ratio:
11 : 4
I Need Help With This Question

Answers
Answer:
Step-by-step explanation:
Dont do it. Just take the detention
Point G is on line segment
F
H
‾
FH
. Given
G
H
=
8
,
GH=8,
F
H
=
3
x
+
3
,
FH=3x+3, and
F
G
=
2
x
,
FG=2x, determine the numerical length of
F
G
‾
.
FG
.
Answers
The numerical length of the line segment FG is 10 units.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables. An independent variable is a variable that does not depend on other variables while a dependent variable is a variable that depends on other variables.
Point G is on FH, hence:
FH = FG + GH
Given that GH = 8, FH = 3x + 3, FG = 2x, hence:
3x + 3 = (2x) + 8
x = 5
FG = 2x = 2(5) = 10
The numerical length of the line segment FG is 10 units.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Tell which set or sets the number below belongs to: natural numbers, whole numbers, integers, rational numbers, irrational numbers, or real numbers.
26
Select all that apply.
O A. rational numbers
B. natural numbers
I c. irrational numbers
D. integers
E. whole numbers
OF. real numbers
Answers
Answer:
A
B
D
E
F
Step-by-step explanation:
26 can be also written as 26/1 or 52/2 or ...
so, it is part of the rational numbers.
it is clearly a natural number (1, 2, 3, 4, ...).
it is also an integer (... , -2, -1, 0, 1, 2, 3, ...).
it is a whole number (0, 1, 2, 3, 4, ...)
and it is a real number, as it can be written as 26.0. real numbers are the superset of all these mentioned sets of numbers.
but it is NOT an irrational number, as they have infinite digits after the decimal point without any repeating pattern.
in other words, any number that is a member of the rational numbers cannot be an irrational number. and vice versa.
Please help me!
The diagram shows the distance time graph of a bus in 45 minutes calculate
a) the period of time that the bus is stationery
b) the speed in km/h¯¹ in the first 5 minutes.
c) the value of s, if the speed is 80 km/h¯¹
d) describe the motion of bus in the last 20 minutes

Answers
Answer:
a) 20 minutes
b) 36 km/h
c) 33.67 km
d) continuous driving without any stationary phases.
Step-by-step explanation:
by the way, speed is specified in distance per time unit. in your example as km/h. and that is how your write this.
not km/h¯¹. that would be wrong, as that would actually be km×h. but you can write e.g. km×h¯¹. that is the same as km/h.
between minutes 5 and 25 there is no progress in distance. so, for these 20 minutes the bus was stationary.
in the first 5 minutes the bus drove 7-4=3 km.
so, in 5 minutes 3 km. to determine the speed we need to calculate up to see, how many km would be have driven in a full hour (60 minutes). the same factor for the time has then to be applied also to the distance to keep the ratio unchanged.
5 × x = 60
x = 12
3 × 12 = 36
so, the speed in these first 5 minutes was 3 km/5 min.
or then in km/h : 36 km/h
between the minutes 25 and 45 the bus drove with a speed of 80km/h.
and the starting point there was at 7 km.
so, the bus drove s-7 km in 20 minutes.
as before, let's first find the scaling factor to deal with a full hour instead of only 20 minutes.
20 × x = 60
x = 3
as before : distance × scaling factor = distance for km/h
(s-7) × 3 = 80
3s - 21 = 80
3s = 101
s = 33.666666666... km
de...
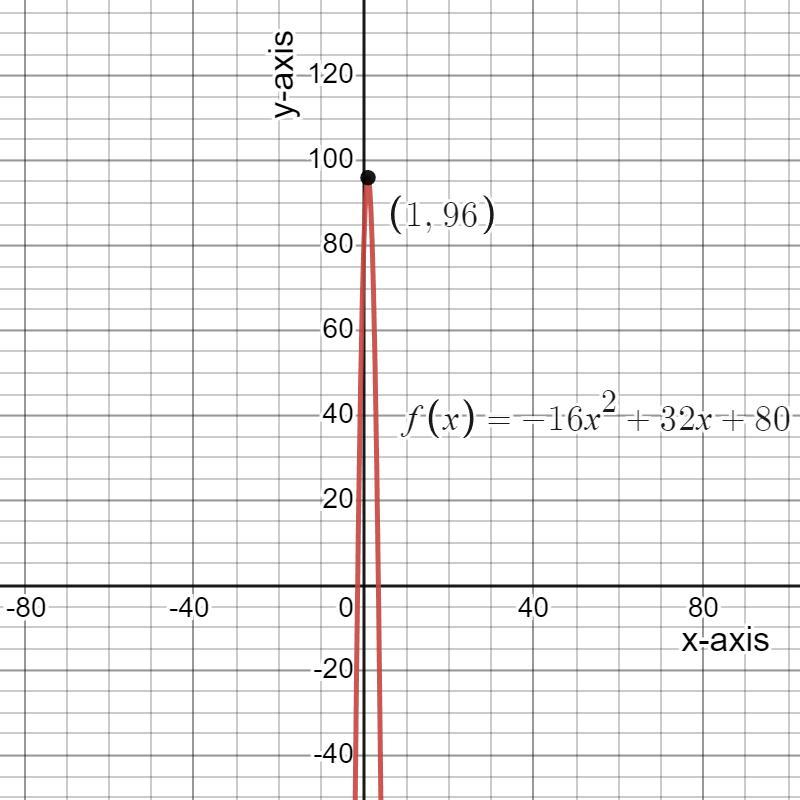
Graphing in Standard Form Check-In
A pebble is tossed into the air from the top of a cliff. The height, in feet, of the pebble over time, in seconds, is modeled by the equation h(t) =
-16² +32t+80. Complete the following sentences. I
It will hit its maximum height after being in the air for
The pebble will reach a maximum

Answers
It will hit its maximum height after being in the air for t = 1 sec.
The pebble will reach a maximum height of 96 units.
Maximum Height refers to an object's highest point as measured from the average natural ground level at the base of the supporting structure.
A stone is thrown into the air from a cliff's edge.
The equation for the height of the pebble over time t is:
h(t) = - 16t² + 32t + 80
When we plot the equation on the graph, we observe that the height of the pebble is maximum when time t = 1.
Therefore,
h(t) = - 16t² + 32t + 80
h(1) = - 16 × (1)² + 32 × 1 + 80
h(1) = - 16 + 32 + 80
h(1) = 16 + 80
h(1) = 96 units
The maximum height of the pebble is 96 units.
Learn more about equation here:
https://brainly.com/question/12446886
#SPJ9
Solve 54=y−14. i need help anything helps.
Answers
Answer:
y=68
Step-by-step explanation:
isolate the variable by adding 14 to both sides
54+14=y+14-14
68=y
