Answers
Solution
Step 1
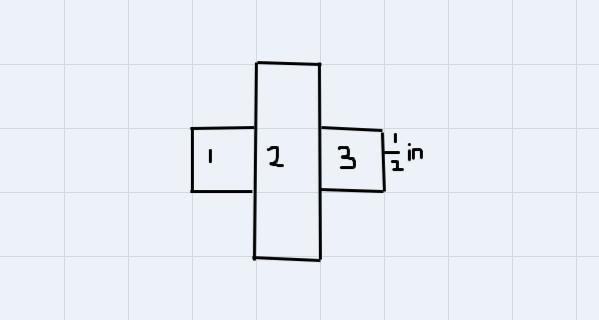
Divide the logo into 3 parts
Step 2
Find the area of each of the three parts and sum
Shape 1 has an area of 1/2 x 1/2 = 1/4 in x 6 ft = 3/2 square ft
shape 3 = 3/2 square ft
shape 2 = 1/2 x 3 x 1/2=3/4 in x6 =9/2 ft
Total area =2(3/2) + 9/2 =15/2 square ft or 7.5 square ft
Related Questions
he square of 9 less than a number is 3 less than the number. What is the number? –12 or 7 –12 or –7 –7 or 12 7 or 12
Answers
Answer:
I thing its 7- 12 sorry if wrong
Step-by-step explanation:
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Gravity acceleration at the Earth surface is 9.81 m/s². What is the acceleration in inches/s² (rounded to the nearest tenth) ?
Answers
Rounded to the nearest tenth, the acceleration in inches per second squared is approximately 15222.8 in/s².
To convert the acceleration from meters per second squared (m/s²) to inches per second squared (in/s²), we need to use the conversion factor between the two units.
1 meter is equal to 39.37 inches.
To convert the units, we can set up the following conversion factor:
1 m/s² = (39.37 in/m)^2 = 1550.0031 in/s²
Now, we can multiply the given acceleration in m/s² by the conversion factor to obtain the acceleration in in/s²:
Acceleration in in/s² = 9.81 m/s² * 1550.0031 in/s²
Acceleration in in/s² ≈ 15222.7568 in/s²
Rounded to the nearest tenth, the acceleration in inches per second squared is approximately 15222.8 in/s².
for such more question on acceleration
https://brainly.com/question/25256383
#SPJ8
a) Work out the size of angle x. b) Give reason for your answer.

Answers
A
x=75°
B
We know that ∠EFG=∠ABF because they are corresponding angles.
We also know that ∠x+∠ABF=180, because angles along a straight line always equal 180:
x+105=180
x=75°
Please answer this correctly without making mistakes I want ace expert and genius people to answer this correctly without making mistakes my homework is due today I have to finish this today

Answers
Answer:
24 i think
Step-by-step explanation:
I evaluated using he given value
If a point Cis inside ZAVB, then m/AVC + mACVB =

Answers
The sum of the measure of angles ∠AVC + ∠CVB is C. ∠AVB.
What is an angle bisector?An angle bisector is a line segment that divides an angle into two equal parts.
The angle addition postulate states, if a line segment is in between an angle sum of two smaller angles created by the line segment, is equal to the measure of the larger angle.
The measure of angle AVB is 62°.
The measure of the angle AVC is 39° and the measure of the
angle CVB is 23°.
As the point, C is inside ∠AVB, ∠AVC + ∠CVB = ∠AVB.
learn more about angles here :
https://brainly.com/question/28451077
#SPJ1
The side of the base of a square pyramid is increasing at a rate of 666 meters per minute and the height of the pyramid is decreasing at a rate of 111 meter per minute. At a certain instant, the base's side is 333 meters and the height is 999 meters. What is the rate of change of the volume of the pyramid at that instant (in cubic meters per minute)
Answers
Answer:
\(105m^3/min\)
Step-by-step explanation:
We are given that
Base side of square pyramid, a=3 m
Height of square pyramid, h=9m
\(\frac{da}{dt}=6m/min\)
\(\frac{dh}{dt}=-1/min\)
We have to find the rate of change of the volume of the pyramid at that instant.
Volume of square pyramid, V=\(\frac{1}{3}a^2h\)
Differentiate w.r.t t
\(\frac{dV}{dt}=\frac{1}{3}(2ah\frac{da}{dt}+a^2\frac{dh}{dt})\)
Substitute the values
\(\frac{dV}{dt}=\frac{1}{3}(2(3)(9)(6)+(3^2)(-1)\)
\(\frac{dV}{dt}=105m^3/min\)
Hence, the rate of change of the volume of the pyramid at that instant=\(105m^3/min\)
which is greater [-3.25] or [4.25]
Answers
Answer:
4.25
Step-by-step explanation:
The number is bigger in absolute form
8 is to 32 as 1 is to
Answers
Answer:
1 is to 4
Step-by-step explanation:
the factor is 1-4 meaning 32÷8 is 4 so having 1 would mean the other factor is 4
-10
A'
9
T
&
-2
В'
N
T
OF
23
-5
-10
2
3
B
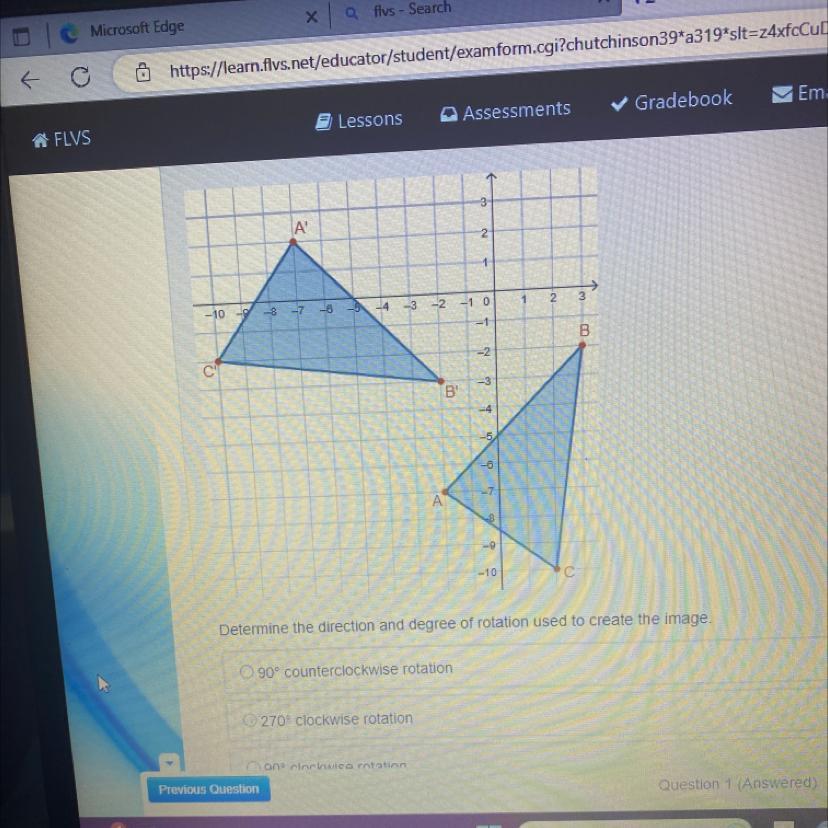
Determine the direction and degree of rotation used to create the image.
Answers
The direction and degree of rotation used to create the image include the following: C. 90° clockwise rotation.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation that moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
By applying either a rotation of 90° clockwise or a rotation of 270° counterclockwise to the coordinate of triangle ABC, the coordinate of its image (triangle A′B′C′);
(x, y) → (y, -x)
Point A = (-2, -7) → Point A′ (-7, 2)
Point B = (3, -2) → Point B′ (-2, -3)
Point C = (2, -10) → Point C′ (-10, -2)
Read more on rotation here: brainly.com/question/28854313
#SPJ1
Complete Question:
Determine the direction and degree of rotation used to create the image.
90° counterclockwise rotation
270° clockwise rotation
90° clockwise rotation
180° clockwise rotation

A table of values of a linear function is shown below. Find the output when the input is . Type your answer in the space provided.
input 1234n
output 6420
Answers
Answer:
The New Deal was a series of programs, public work projects, financial reforms, and regulations enacted by President Franklin D. Roosevelt in the United States between 1933 and 1939
5. Prove that each of the expressions below are equivalent by evaluating the
expressions given that p=2.
I
4(p-5) - 8
4p - 28

Answers
Answer:
4P -28 Step-by-step explanation:
Answer:
Both expression give -12
Step-by-step explanation:
4(p - 5) - 8
4p - 20 - 8
p = 2
4(2) - 28
8 - 20
- 12
4p - 28
p = 2
4 ( 2) - 28
8 - 28
-12
Hi can someone who is great at math please help me with these math questions. I'm struggling with them!!


Answers
The value of x will be 18.67 for the given data of the triangle.
We have,
Thale's theorem:
When a line parallel to one side of a triangle intersects the other two sides in distinct points, the other two sides are divided in the same ratio.
Given that the sides of the triangle are divided into two parts,
For the left part the parts will be x and x + 7 for the right side the parts will be 16 and 22.
The ratio will be the same according to Thale's theorem. The value of x will be calculated as:-
x / ( x + 7 ) = 16 / 22
22x = 16x + 112
6x = 112
x = 112 / 6
x = 18.67
Therefore, the value of x will be 18.67.
To know more about Thale's theorem follow
brainly.com/question/14417137
#SPJ1
complete question;
Find the values of x and y. Find value of x.
In triangle ABC acute angles are in the ratio 5:1, i.e.
Answers
Answer:
The quen is as following:
ABC is a right triangle at C,
Acute angles are in the ratio 5:1, i.e. ∠BAC : ∠ABC = 5:1
If CH is an altitude to AB and CL is an angle bisector of ∠ACB, find m∠HCL.
The solution is: m∠HCL = 30°
Step-by-step explanation:
See the attached figure.
∵The triangle is right at C ∴∠C = 90°
∴∠A + ∠B = 90° ⇒(1)
∵ Acute angles are in the ratio 5:1, i.e. ∠BAC : ∠ABC = 5:1
∴∠A = 5 times ∠B
Substitute at (1)
∴ 5 ∠B + ∠B = 90° ⇒⇒⇒ ∴∠B = 15° and ∠A = 75°
∵CL is an angle bisector of ∠ACB
∴ ∠ACL = 90°/2 = 45°
∵ CH is an altitude to AB ⇒ ∠CHA = 90°
At the triangle AHC:
∠ACH = 180° - (∠CHA + ∠CAH) = 180° - (90° + 75°) = 15°
∴ ∠HCL = ∠ACL - ∠ACH = 45° - 15° = 30°
0.5/10=0.05 how do you know?
Answers
Answer:
I know because all you have to do is keep the number the same then add how many 0 is behind the 10 which is 1 so you put however many number that is behind the decimal behind the decimal if you know what i mean .
Step-by-step explanation:
helo please show work

Answers
Answer:
Step-by-step explanation:
Solution:
We can simplify the ratio 305 : 60 by dividing both terms by the greatest common factor (GCF).
The GCF of 305 and 60 is 5.
Divide both terms by 5.
305 ÷ 5 = 61
60 ÷ 5 = 12
Therefore:
305 : 60 = 61 : 12
At a military function, three cannons are fired at intervals of 12
seconds. 16 seconds and 18 seconds respectively. If the three cannons
are fired together initially, after how many seconds will they all be
fired together again?
please give me an answer I give you an Brainalist
Answers
Answer:
144 seconds
Step-by-step explanation:
To do solve this question, we must find the LCM (least common multiple) of 12, 16, and 18.
Let's start by prime factorizing (finding the prime factors) all the numbers.
\(12\rightarrow3*4\rightarrow2*2*3\)
\(16\rightarrow4*4\rightarrow2*2*2*2\)
\(18\rightarrow2*9\rightarrow2*3*3\)
Now, we must find the greatest quantity of each [prime] number and multiply them together to obtain the least common multiple.
Upon further evaluation of the [prime] factors, we can see that we need four 2s and two 3s. Therefore...
\(2*2*2*2*3*3=2^4*3^2=16*9=144\)
They will be fired together again after 144 seconds.
00:00
Muriel has been a member of the Solaris Gym for 372 days,
Ben has been a member for 1 year, 2 weeks, 3 days.
Part A
Who has been a member of the Solaris Gym longer?
Use the drop-down menus to show and explain your answer.
Choose...
has been a member longer because 1 year, 2 weeks, 3 days is
Choose...
than 372 days
00:00
Part B
How much longer? Assume that it is not a leap year. Enter your answer in the box.
days
Answers
Answer:
A: Ben has been a member longer because 1 year, 2 weeks, 3 days is longer than 372 days.
B: 10 days longer
Step-by-step explanation:
1 year, 2 weeks, 3 days is 382 days -> 365 + 14 + 3 = 382
SOMEONE HELP AS SOON AS POSSIBLE!!!! please:))

Answers
Therefore y = [8 (root 3)] / 3
Using Pythagorean Theorem we know
x^2 = a^2 + b^2
x = (root 384) / 9
x = [ 8 (root 6) ] / 9
An airplane descends during the last hour of it's flight to prepare for landing. It's altitude changes at an average of -0.15 km per minute for those 60 minutes. Write an expression to represent the total change in the airplane's elevation. ( plz answer, will give brainliest )
Answers
Answer:
-.15 km/ minute * 60 minutes
-9 km
Step-by-step explanation:
The rate is -.15 km per minute
We have 60 minutes
distance = rate times time
change in elevation is the same as the distance change
change in elevation = -.15 km/ minute * 60
change in elevation =-9 km
Answer:
(0.15 km/min) * (60 min)
Step-by-step explanation:
We see that the plane descends 0.15 kilometres every minute over the span of 60 minutes.
Use the distance-rate-time formula: d = rt, where d is the distance, r is the rate, and t is the time.
Here, our rate is r = 0.15 km/min and our time is t = 60 minutes. Then the total change in elevation is:
d = rt
d = 0.15 * 60 = 9 km
Note that we disregard the negative sign from -0.15 km/min because the question is asking for the change in elevation. Change is never a negative value.
Hence, the expression will be: 0.15 * 60, which simplifies to 9 km.
~ an aesthetics lover
Plss help!
Calculate the area of the irregular polygon shown below:
A. 24 square inches
B. 44 square inches
C. 54 square inches
D. 84 square inches

Answers
The area of the irregular polygon is 24 square inches. Hence option A is the correct option.
What is an irregular polygon?
An irregular polygon does not have all of its sides equal, nor are all of its angles equal in size. Scalene triangles, right triangles, isosceles triangles, rectangles, parallelograms, irregular pentagons, irregular hexagons, and so on are examples of irregular polygons.
The length of DE is 5 in and HI is 5in.
The length of AL is 12in.
The length of AD + EH + IL = AL - (DE+HI) = 12 - (5+5) = 2 in
The length of AB = DC = EF = HG = IJ = LK = 7in.
The sum area of the rectangles ABCD, EFGH, and IJKL is
AB×AD + EF×EH + IJ×IL
= 7×AD + 7×EH +7×IL
= 7(AD + EH + IL)
= 7×2
= 14 square inches
The length of DW = EX = HY = IZ = 7 - 6 = 1in.
The area of DWXE is DW×WX = 1×5 = 5 square inches
The area of HYZI is HY×YZ = 1×5 = 5 square inches
The area of the irregular polygon is
14 + 5 + 5 square inches
= 24 square inches
To learn more about area of a polygon, click on the below link:
https://brainly.com/question/3886316
#SPJ1

What is the prime factorization of 144? A) 2.72 B) 24 • 32 I C) 12.12 D) 22 • 62
Answers
Answer: So maybe D or B.
Step-by-step explanation:2to the 4-power x 3 to the 2nd power.
For what value or p will the function be continuous . Btw it’s number 5 not 6

Answers
SOLUTION
Looking at the piecewise function, what will make p continuous is the value of x common to both, looking at it, from the range of values
\(\begin{gathered} -7\leq x\leq-1 \\ -1-1 is common to both. So we will substitute -1 for x into the equations, equate them and solve for p, we have \(\begin{gathered} x^2+4x-1 \\ (-1)^2+4(-1)-1 \\ 1-4-1=-4 \end{gathered}\)and
\(\begin{gathered} -3x+p \\ -3(-1)+p \\ 3+p \end{gathered}\)equating we have
\(\begin{gathered} -4=3+p \\ -4-3=p \\ -7=p \\ p=-7 \end{gathered}\)Hence the answer is -7
Find the value of x in the parallelogram

Answers
The value of x in the parallelogram is 112°.
In a parallelogram, adjacent angles are always supplementary. This means that the sum of two adjacent angles in a parallelogram is always 180 degrees.
To understand this concept, let's consider a parallelogram ABCD. The opposite sides of a parallelogram are parallel and equal in length, and the opposite angles are congruent. Adjacent angles are those that share a side. Let's say angle A and angle B are adjacent angles in the parallelogram.
Since opposite angles of a parallelogram are congruent, we have angle A is congruent to angle C, and angle B is congruent to angle D.
Now, let's consider angle A and angle B. The sum of angle A and angle B is equal to the sum of angle C and angle D because opposite angles are congruent.
Therefore, we can conclude that angle A + angle B = angle C + angle D = 180 degrees.
This property holds true for all parallelograms. So, in any parallelogram, the adjacent angles are always supplementary, meaning their sum is 180 degrees.
For the given question, we know x° + 68° = 180°.
Then x° = 180° - 68°
x° = 112°
For more such questions on parallelogram
https://brainly.com/question/20526916
#SPJ8
Set up the appropriate equation to solve for the missing angle.

Answers
65^2 = 4,225
46^2 = 2,116
To find the missing angle, we must subtract 2,116 from 4,225 and then identify the difference’s square root.
4,225 - 2,116 = 2,109
√2,109 ≈ 45
Hence, x ≈ 45.
Answer:
Using the Pythagorean Theorem, we know x^2 + 46^2 is equal to 65^2. With that in mind, it is important to note:
65^2 = 4,225
46^2 = 2,116
To find the missing angle, we must subtract 2,116 from 4,225 and then identify the difference’s square root.
4,225 - 2,116 = 2,109
√2,109 ≈ 45
Hence, x ≈ 45.
Step-by-step explanation:
The volume of the polyhedron is ______ cm3.

Answers
No work needed to show just answer

Answers
Answer:
1.62 × 10⁸
hope it helps!
A searchlight rotates through one complete revolution every 36 seconds. How long does it take the light to rotate through 90°?
Answers
Answer: 1 second
1 full revolution=360
4seconds=360degrees
how many seconds are 90 degrees
4:360=x:90
4/360=x/90
simplify
1/90=x/90
1=x
the answer is 1 second
Step-by-step explanation:
Hope this helps you!!!!!!!!! :D
360° can be divided by 9° into 4 parts. 36 divided by 4 is 9
The pumpkin patch had two corn mazes, as shown by the shaded and non-shaded sections in the model below.
A model with 4 rows of 7 squares, representing 28 acres, and 2 rows of 7 squares, representing 14 acres.
Which expression is shown by the model?
Answers
Answer :
D - 28 + 14 = 7(4+2)
This figure shows an oblique triangle-based pyramid.
What is the volume of the figure?

Answers
Answer: 88 cm^3
Step-by-step explanation:
= 1/2 • bh
= 1/2 • 6 • 8
= 24
= 1/3 • 24 • 11
= 88 cm^3
The volume of the oblique triangle-based pyramid, having dimensions 6 cm, 8 cm, 11 cm, and 36.2 cm, is 88 cm³.
What is volume?The capacity occupied by a three-dimensional solid shape is known as volume. It is difficult to visualize in any shape, yet it may be compared among shapes. For instance, a compass box has a larger volume than an eraser placed inside of it.
Given:
The dimension of the pyramid are 6 cm, 8 cm, 11 cm, and 36.2 cm,
Calculate the volume as shown below,
The Volume of the pyramid = 1 / 3 × Area of the triangle × height
The volume of the pyramid = 1 / 3 × 1 / 2 × 6 × 8 × 11
The volume of the pyramid = 528 / 6
The volume of the pyramid = 88
Thus, the volume of the pyramid is 88 cm³.
To know more about volume:
brainly.com/question/13807002
#SPJ2
