Find tan theta if theta is an angle in standard position and the point with coordinates (4,3) lies on the terminal side of the angle
Answers
Answer: 0.75
Step-by-step explanation:
We can do this by drawing a terminal side in a standard position and then drawing the associated triangle. We then use the Pythagoras theorem to find the missing side the hypotenuse. Then, this will give a Pythagorean Triplet of 3, 4 and 5.
We now have a triangle with the values of:
x = 4
y =3
h^2= 4^2 + 3^2
h^2 = 16 + 9
h^2 = 25
h = 5
h = 5
Tangent = opposite/adjacent
= y/x
= 3/4
= 0.75
Related Questions
Please help! Im a struggling depressed student that needs to desperately catch up.

Answers
Answer:
25%
Step-by-step explanation:
30/120 = 1/4
1/4 = 25%
Susan has a collection of 98 nickels and dimes. If the number of nickels is six times the number of dimes, how many nickels and how many dimes does she have?
Answers
Answer:
14 (nickels)84 (dimes)
Step-by-step explanation:
Susan has a collection of 98 nickels and dimes. If the number of nickels is six times the number of dimes, how many nickels and how many dimes does she have?
nickels = x
dimes = 6x
6x + x = 7x
98 : 7 = 14 (nickels)
14 x 6 = 84 (dimes)
-----------------------
14 + 84 = 98 (the answer is good)
The difference of a number and eight is equal to 14.
Answers
"A number" means the unknown.
"Difference" means to subtract.
We already know two numbers, 8 and 14, but we don't know "A number."
We can put v as our variable. You can put any type of letter.
Therefore, the answer is: v - 8 = 14
factorise
x² + 5x - 14
Answers
A _____ divides a segment or angle in half.
will give brainliest !!
ig- 513_kaylee
tiktok- ..theekaylee
sc- kkcutie14
Answers
Answer:
Bisector
Step-by-step explanation:
Brainliest pls
Answer:
the answer is the bisector
V2 is in between what two numbers??

Answers
Answer:
sqrt of 2 is between 1 and 2
The square root of 2 is in between the square of one and the square of 2.
How do you find the moment of inertia of multiple bodies?
Answers
Answer: To find the moment of inertia of multiple bodies, we need to use the parallel axis theorem. The parallel axis theorem states that the moment of inertia of a body about any axis parallel to its centroidal axis is equal to the moment of inertia about the centroidal axis plus the product of the body's mass and the square of the distance between the two axes.
Here are the steps to find the moment of inertia of multiple bodies:
Find the moment of inertia of each body about its centroidal axis using the appropriate formula for that body. For example, the moment of inertia of a solid cylinder about its central axis is 1/2MR^2, where M is the mass of the cylinder and R is the radius of the cylinder.
Determine the centroid of the system of bodies. This is the point through which the axis of rotation passes and is the point about which the moment of inertia is calculated.
Calculate the distance between the centroid and each body's centroidal axis.
Use the parallel axis theorem to find the moment of inertia of each body about the axis passing through the centroid of the system. Add up all the moments of inertia of each body about the centroid of the system to get the total moment of inertia.
The formula for the parallel axis theorem is:
I = I_cm + md^2
where I is the moment of inertia about the axis passing through the centroid of the system, I_cm is the moment of inertia about the centroidal axis of the body, m is the mass of the body, and d is the distance between the two axes.
By using this formula, we can find the moment of inertia of any system of bodies with respect to any axis parallel to the centroidal axis.
Step-by-step explanation:
Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
Need help with math problem give 5 stars and brain thingy point

Answers
Answer:
b) 2/6
Step-by-step explanation:
0, 1/6, 2/6, 3/6, 4/6, 5/6, 1
Hope this helps!
two partners divide a profit of $2,000 so that's a difference between the two amounts is half of their average. what is the ratio of the larger to the smaller amount?
Answers
Answer:
5/3
Step-by-step explanation:
The partners have a total profit of $2000. Since there are only 2 partners, then the average profit each one makes is $2000/2 = $1000.
The difference between the 2 amounts is half of the average, so it is $1000/2 = $500.
One amount is x.
The other amount is x + 500
The sum is 2000
x + x + 500 = 2000
2x + 500 = 2000
2x = 1500
x = 750
x + 500 = 750 + 500 = 1250
The partners had profit of $1250 and $750.
The ratio is 1250/750 = 125/75 = 5/3
Answer: 5/3
The ratio of the larger to the smaller amount will be 5 : 3
What are ratios?
A ratio says how much of one thing there is compared to another thing. We can write the ratio as -
x : y
{x/y} = k
x = ky
[k] is called the scale factor.
Given is that two partners divide a profit of $2,000 so that's a difference between the two amounts is half of their average.
Assume that the amount with partner [1] is $[x] and with partner [2] is $[y]
. So, we can write according to the question as -
x + y = 2000 ......Eq [1]
x - y = {1/2 x (x + y)/2} ......Eq [2]
Now -
x - y = {1/2 x (2000/2)}
x - y = {1/2 x 1000}
x - y = 500
x = 500 + y
So, we can write the equation [1] as -
x + y = 2000
500 + y + y = 2000
2y = 1500
y = 750
So, [x] will be equivalent to -
x = 2000 - 750
x = 1250
The ratio of the larger to the smaller amount will be -
x/y = 1250/750 = 250/150 = 50/30 = 5/3
Therefore, the ratio of the larger to the smaller amount will be 5 : 3.
To solve more questions on ratios, visit the link below -
https://brainly.com/question/29079409
#SPJ2
show that the points ( 4,9,6) (-1,6,6 ) and (0,7,10) form an isosceles right angled triangle. find the perimeter of the triangle.
Answers
The perimeter of the triangle is the sum of the lengths of its sides, which is: 12.24
Explanation:
To show that the given points form an isosceles right angled triangle, we first need to find the lengths of the sides of the triangle using the distance formula.
Let the given points be A(4, 9, 6), B(-1, 6, 6), and C(0, 7, 10).
The distance between points A and B is given by:
AB = sqrt((4 - (-1))^2 + (9 - 6)^2 + (6 - 6)^2) = sqrt(5^2 + 3^2 + 0^2) = sqrt(34)
The distance between points A and C is given by:
AC = sqrt((4 - 0)^2 + (9 - 7)^2 + (6 - 10)^2) = sqrt(4^2 + 2^2 + 4^2) = 2*sqrt(6)
The distance between points B and C is given by:
BC = sqrt((-1 - 0)^2 + (6 - 7)^2 + (6 - 10)^2) = sqrt(1^2 + 1^2 + 4^2) = sqrt(18)
Now, we can see that the triangle ABC is not isosceles since all three sides have different lengths.
To check if the triangle is right-angled, we can use the Pythagorean theorem. If the square of the length of the longest side is equal to the sum of the squares of the other two sides, then the triangle is right-angled.
Here, the longest side is AC with length 2*sqrt(6), so we need to check if:
AC^2 = AB^2 + BC^2
4*6 = 34 + 18
24 = 52
This equation is not true, so the triangle ABC is not a right-angled triangle.
Therefore, the given points do not form an isosceles right angled triangle.
The perimeter of the triangle is the sum of the lengths of its sides, which is:
AB + AC + BC = sqrt(34) + 2*sqrt(6) + sqrt(18) ≈ 12.24
To learn more about isosceles right angled triangle visit:https://brainly.com/question/30381855
#SPJ11
Select the Ordered Pair which is a solution to the equation. y=6x+9
(−4, −11)
(−3, −9)
(−2, −7)
(−1, −5)
Answers
Answer:
(−3, −9)
Step-by-step explanation:
(−4, −11)
y=6x+9
-11 = 6(-4) + 9
-11 = -15
False
(−3, −9)
y=6x+9
-9 = 6(-3) + 9
-9 = -9
True
(−2, −7)
y=6x+9
-7 = 6(-2) + 9
-7 = -3
False
(−1, −5)
y=6x+9
-5 = 6(-1) + 9
-5 = 3
False
from a collection of 51 store customers, 2 are to be chosen to receive a special gift. how many groups of 2 customers are possible?
Answers
From the question above, we can know the groups of 2 customers that are possible to be chosen to receive a special gift is 1,275 groups.
How to find possibility of combination?
To find possibility of combination like in the question above, we can use binomial coefficient formula. The binomial coefficient is about two things with two result. The formula of binominal coefficient is \(\binom{n}k} = \frac{n!}{k! (n - k)!}\)
Anyone of the 51 can be chosen first and any of the remaining 50 can be chosen second. Or in which 2 of the 51 can be chosen ⇒ 51 x 50
But, for any given group of 2, the number of different orders in which they could have been chosen is 2 x 1.
So, the numbers of different combination of 2 chosen from 51 is:
\(\binom{51}2} = \frac{51 x 50}{2 x 1}\)
\(\binom{51}2} = \frac{2,550}{2} = 1,275\)
Learn more about Binomial Coefficient here: https://brainly.com/question/2745427
#SPJ4
Solve logx (512) = 3
Show/Explain your thought process
Need help quick please ToT
Answers
The value of x is after solving the logarithm equation logx⁽⁵¹²⁾ = 3 is 8.
What is a logarithm equation?A logarithmic equation is an equation that involves the logarithm of an expression containing a variable.
To solve the logarithm equation, we follow the steps below.
Given:
logx⁽⁵¹²⁾ = 3Step 1:
Take log to the other side of the equation.Note: When logarithm cross the equality sign, it becomes an indices.Therefore,
512 = x³Step 2:
Convert 512 to index form. (i.e 8³)
8³ = x³...................... Equation 1Comparing both side of equation 1,
x = 8.Hence, the value of x is 8.
Learn more about logarithm here: https://brainly.com/question/25993029
#SPJ1
Help please, I need it


Answers
Answer:
2) c) (x-3)² + (y+2)² = 25
5) x^2 +y^2 -8x -16y +54 = 0
6) x^2 +y^2 -10x -12y +36 = 0
Step-by-step explanation:
2) The standard form equation for a circle is ...
(x -h)^2 +(y -k)^2 = r^2
You are given the center: (h, k) = (3, -2) and a point on the circle. So, the equation will be ...
(x -3)^2 +(y +2)^2 = r^2
Since we know a point on the circle we know that ...
(7 -3)^2 +(1 +2)^2 = r^2 = 16 +9 = 25
So, the circle's equation is ...
(x -3)^2 +(y +2)^2 = 25 . . . . . matches choice C
__
5) As in the previous problem, the standard form equation is ...
(x -4)^2 +(y -8)^2 = (-1-4)^2 +(7-8)^2 = 25+1 = 26
To put this in general form, we need to subtract 26 and eliminate parentheses.
x^2 -8x +16 +y^2 -16y +64 -26 = 0
x^2 +y^2 -8x -16y +54 = 0
__
6) A circle tangent to the y-axis will have a radius equal to the x-value of the center point.
(x -5)^2 +(y -6)^2 = 5^2
x^2 -10x +25 +y^2 -12y +36 = 25
x^2 +y^2 -10x -12y +36 = 0

2 2/9+1 4/9 in simplest form
Answers
Answer:
\(2 \frac{2}{9} + 1 \frac{4}{9} \\ = \frac{20}{9} + \frac{13}{9} \\ = \frac{33}{9} \\ = 3 \frac{2}{3} \\ \\ { \underline{ \blue{ \tt{⚜becker \: jnr}}}}\)
What is the greatest common factor of the polynomial:
15x^5 +10x^4+25x^3
Answers
Step-by-step explanation:
15x^5 +10x^4+25x^3
5x³(3x²+2x+5)
Answer:
5x^3
Step-by-step explanation:
I have no idea how to explain this but here we go
If we were to factor, we first look at all the numbers, not the variables and their exponents.
So we have: 15, 10, and 25, and the greatest common factor is 5
So 5 is going to be part of our final answer.
Then, we look at all the x's and the exponents on them
So we have: x^5, x^4, x^3,
The smallest out of all of them is x^3.
So that's going to be part of your answer
and since it's multiplication
bam, you join them together to make it 5x^3
I hope this helped, let me know if you have any questions
Consider the line 3x+8y=1what is the slope of a line parallel to this line?what is the slope of a line perpendicular to this line?
Answers
To find the slope of the line given, we write the equation in slope-intercept form:
\(y=mx+b\)For the equation,
\(3x+8y=1\)subtracting 3x from both sides gives
\(8y=1-3x\)Finally, dividing both sides by 8 gives
\(y=\frac{1-3x}{8}\)which can be rearranged and written as
\(y=-\frac{3}{8}x+\frac{1}{8}\)Hence, the slope of the line parallel to the given line is -3/8.
To find the slope of the perpendicular line, we have to remember that
\(m_{\perp}=-\frac{1}{m}\)Since m = -3/8, the above gives
\(m_{\perp}=-\frac{1}{(-\frac{3}{8})}\)Simplifying the above gives
\(m_{\perp}=\frac{8}{3}\)Hence, the slope of the perpendicular line is 8/3.
The diameter of the circle is 34cm and a chord is at a distance of 15cm from
the centre. Find the length of the chord of the circle. circles chapter
Answers
Answer:
16
Step-by-step explanation:
d=34
r=17
Im just gonna use the picture to help explain
to get AP we can use the pythagoras theorem
\( {17}^{2} - {15}^{2} = {ap}^{2} \)
\(289 - 225 = {ap}^{2} \)
\(64 = {ap}^{2} \)
Therefore AP =8
AB=AP+PB
AP=PB. (line perpendicular to chord bisects chord)
Therefore AB=16

The temperature was 8 degrees below zero at 5 A.M. By 1 P.M. the temperature had risen 23 degrees. What was the temperature at 1 P.M.?
Answers
Answer:
15 degrees
Step-by-step explanation:
What is the equation of the line that passes through the point (-9,6) and is perpendicular
to the line 3x-5?
M
Oy--x-3
О У - 3x + 21
Oy - 3x +33
Answers
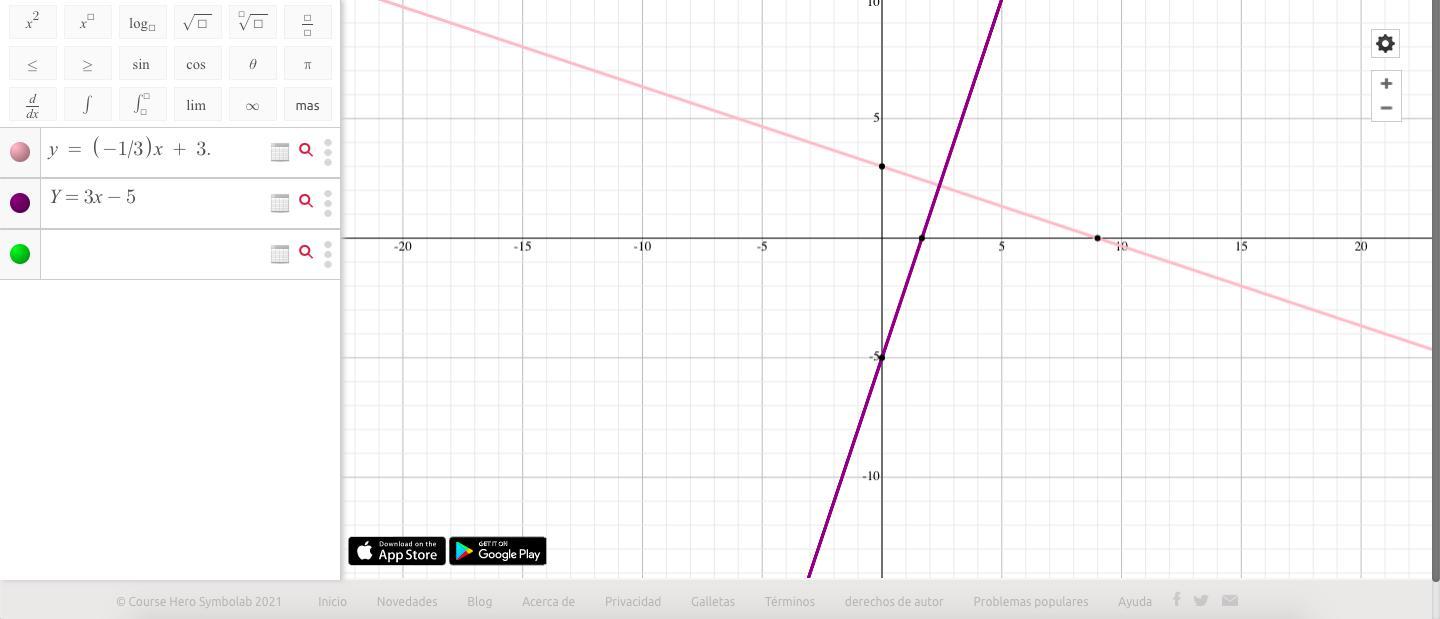
Answer:
y = (-1/3)x + 3.
Step-by-step explanation:
To find the equation of a line perpendicular to a given line, we need to take the negative reciprocal of the slope of the given line.
The slope of the given line Y=3x-5 is 3. Therefore, the slope of a line perpendicular to this line would be -1/3.
Now, using the point-slope form of a line, we can write the equation of the line passing through (-9,6) and having a slope of -1/3:
y - 6 = (-1/3)(x - (-9))
Simplifying:
y - 6 = (-1/3)x - 3
y = (-1/3)x + 3
Therefore, the equation of the line that passes through (-9,6) and is perpendicular to the line Y=3x-5 is y = (-1/3)x + 3.
The difference of smallest eight digit number and greatest seven digit number is
Answers
Answer:
8 digit smallest number is 10000000. 7 digit largest number is 9999999.
Step-by-step explanation:
In a histogram, the vertical line (dimension) shows the _____________, while the horizontal line (dimension) shows the _______________.
Answers
In the Histogram the horizontal line (dimension) represents the value of the selected collection plan element. The vertical line (dimension) represents the count or sum of occurrences of the primary collection element on the horizontal line.
learn more about Histogram here:
https://brainly.com/question/1230107
#SPJ1
A singing contest eliminated contestants after each round the number of contestants that go into round N is equal to the number of contestants in the previous round, raised to the (n-1/n)-th power, rounded to the nearest integer. The number of contestants in around two is 243. How many contestants will be in around five
Answers
The number of contestants in round 5 is 128.
The formula used to calculate the number of contestants in round N is:
Number of contestants in round N = (Number of contestants in round N-1)^((N-1)/N), rounded to the nearest integer.
Given that the number of contestants in round 2 is 243, then the number of contestants in round 5 can be calculated as follows:
Number of contestants in round \(5 = 243^((5-1)/5)\), rounded to the nearest integer
Therefore, the number of contestants in round 5 = 128.
To summarize, the number of contestants in round 5 is 128, which is calculated by raising the number of contestants in the previous round (round 2) to the ((N-1)/N)-th power and rounding the result to the nearest integer.
Learn more about integer here:
https://brainly.com/question/15276410
#SPJ4
solve sinx = 2x-3 using false position method
Answers
The root of the equation sinx = 2x-3 is 0.8401 (approx).
Given equation is sinx = 2x-3
We need to solve this equation using false position method.
False position method is also known as the regula falsi method.
It is an iterative method used to solve nonlinear equations.
The method is based on the intermediate value theorem.
False position method is a modified version of the bisection method.
The following steps are followed to solve the given equation using the false position method:
1. We will take the end points of the interval a and b in such a way that f(a) and f(b) have opposite signs.
Here, f(x) = sinx - 2x + 3.
2. Calculate the value of c using the following formula: c = [(a*f(b)) - (b*f(a))] / (f(b) - f(a))
3. Evaluate the function at point c and find the sign of f(c).
4. If f(c) is positive, then the root lies between a and c. So, we replace b with c. If f(c) is negative, then the root lies between c and b. So, we replace a with c.
5. Repeat the steps 2 to 4 until we obtain the required accuracy.
Let's solve the given equation using the false position method.
We will take a = 0 and b = 1 because f(0) = 3 and f(1) = -0.1585 have opposite signs.
So, the root lies between 0 and 1.
The calculation is shown in the attached image below.
Therefore, the root of the equation sinx = 2x-3 is 0.8401 (approx).
Learn more about equation
brainly.com/question/29657983
#SPJ11
A certain rectangular prism has a height of 4 m, a length of 3 m, and a width of 7 m. Give the dimensions of a second rectangular prism that will have the same surface area of the first one.
PLEASE HELP 50 POINTS
Answers
To find the dimensions of the second rectangular prism that will have the same surface area as the first one, we can use the formula for the surface area of a rectangular prism which is:
Surface Area = 2lw + 2lh + 2wh
where l is the length, w is the width, and h is the height of the rectangular prism.
For the first rectangular prism, we have:
l = 3 m w = 7 m h = 4 m
Surface Area = 2lw + 2lh + 2wh Surface Area = 2(3)(7) + 2(3)(4) + 2(7)(4) Surface Area = 42 + 24 + 56 Surface Area = 122 m²
To find the dimensions of the second rectangular prism that will have the same surface area as the first one, we can use this formula again and solve for one of the variables. Let’s solve for l:
Surface Area = 2lw + 2lh + 2wh 122 = 2l(w+h) + 2wh 122 = 2l(w+h) + w(4) 122 = 2l(w+h) + 4w 118 = l(w+h)
Now we can choose any value for w and h and solve for l. Let’s choose w=1 and h=1:
118 = l(1+1) 118 = l(2) l = 59
So the dimensions of the second rectangular prism that will have the same surface area as the first one are:
l = 59 m w = 1 m h = 1 m
Sally is going to paint the 4 walls in her bedroom. Her bedroom is 3.5 m long , the breth is 2.8 m and 2.2 m high.
the door and window from her bedroom are together 3.2 m².
With one can of paint she can paint 4.5 m².
how much cans of paint does sally need?
Answers
I need help with this question too but less hope we get a answer
Find the volume of the solid whose base is a circle of radius 5, if slices made perpendicular to the base are isosceles right triangles with one leg on the base. (express numbers in exact form. Use symbolic notation and fractions where needed. )
V = ____
Answers
The solid has a 62.5 cubic unit volume. Finding the volume of a solid with a circular base of radius 5 units is the task at hand.
The following formula can be used to determine how much of the magical potion is left after a specific period of time:
Let h represent the solid's height. The volume can therefore be stated as follows:
V = (12.5 dh from 0 to h)
Combining, we obtain:
V = 12.5h
The height of the solid is equal to the radius of the circle, which is 5 units, because the slices are perpendicular to the base. Therefore:
V=12.5h=12.5(5)=62.50 cubic metres
Thus, the solid has a 62.5 cubic unit volume.
Learn more about the volume here:
https://brainly.com/question/28368781
#SPJ4
Please help me with this!!!!

Answers
Office Supplies: The Office Supplies account started the year with a $4,000 debit balance. During the year, the company purchased supplies for $13,400, which added to the Office Supplies Account. The inventory of supplies available at the end of the year totaled $2,554.1. The beginning balance of Office Supplies: 2. The amount to be adjusted (show your calculation): 3. The ending balance of the account after the adjustment (show your calculation):4. Adjusting Journal Entry (please include description): Date Account Debit Credit
Answers
1.The beginning balance should be $4,000
2.The amount to be adjusted is $2554
3.The ending balance of the account after the adjustment $2554
4. Office Supplies Account is $14846
Adjusting entry:An adjusting entry is an additional journal entry that is made at the end of the month or year. When any financial transaction is incurred for which the amount is not accrued yet or no financial transaction incurred for the accrued amount and in such case the adjusting entry is made to know the actual amount accrued in the month or year.
The adjustment entries are the additional entries to the recorded journal entries.
"Information available from the question"
The Office Supplies account started the year with a $4,000 debit balance
The company purchased supplies for $13,400,
The inventory of supplies available at the end of the year totaled $2,554.
Now, According to the question:
1. The beginning balance should be $4,000
2.The adjusted amount is
Opening balance = 4000
Add: New purchases = 13400
Balance after Purchase = 17400
Less: Year end balance = 2554
3. The ending balance is $2,554
4. The adjusting journal entry is
Dr. Supplies Expense Account is 14846
Adjustment in the year = Cr. 14846 (subtracted from the balance)
Office Supplies Account is 14846
Learn more about Account at:
https://brainly.com/question/22917325
#SPJ4