Find a value of the standard normal random variable z , call it. z 0z0,such that the following probabilities are satisfied. a.P(zless than or equals≤z 0z0)equals=0.09730.0973
e.P(minus−z 0z0less than or equals≤zless than or equals≤0)equals=0.25792579
b.P(minus−z 0z0less than or equals≤zless than or equals≤z 0z0)equals=0.9595
f.P(minus−33less than
c.P(minus−z 0z0less than or equals≤zless than or equals≤z 0z0)equals=0.9090
g.P(zgreater than>z 0z0)equals=0.5. d.P(minus−z 0z0less than or equals≤zless than or equals≤z 0z0)equals=0.82148214
h.P(zless than or equals≤z 0z0)equals=0.00310.003
Answers
The value of the standard normal random variable z call it. z 0z0,such that the following probabilities are satisfied:
The standard normal distribution is a special type of normal distribution where the mean is 0, and the standard deviation is 1.
a) P(: 0.0973)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
\(\mathbf{\therefore z_o={\color} \mathbf{-1.30}}}\)
(b) P( Z 0.95)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
P(Z1.96) = 0.95
\(\mathbf{\therefore z_o={\color{} 1.96}}\)
\({\color{} \mathbf{(c)}}\;P(-z_o\leq Z\leq z_o)=0.90\)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
\(\Rightarrow P(Z\leq 1.64)=0.95\)
\(\mathbf{\therefore z_o={\color{} 1.64}}\)
\({\color{} \mathbf{(d)}}\;P(-z_o\leq Z\leq z_o)=0.8214\)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
\(\Rightarrow P(Z\leq 1.35)=0.9107\)
\(\mathbf{\therefore z_o={\color{} 1.35}}\)
(e) \(\Rightarrow P(Z\leq z_o)=0.7579\)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
\(\mathbf{\therefore z_o={\color{} 0.70}}\)
(f) P(Z =0.9588)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
Zo = 1.74
\({\color{} \mathbf{g)}}\;P(z > z_o)=0.5\)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
\(\mathbf{\therefore z_o={\color{} \mathbf{0.00}}}\)
\({\color{} \mathbf{h)}}\;P(z\leq z_o)=0.0031\)
Lookup the Z-value corresponding to the region 0.0973 to the left of the normal curve in the Z-table or use the excel formula " =NORM.S.INV(0.0975) " to get the probability.
\(\mathbf{\therefore z_o={\color{} \mathbf{-2.74}}}\)
Learn more about Standard normal variable:
https://brainly.com/question/26822684
#SPJ4
Related Questions
Help please ASAP thank you!!
And no links please no linksss!!

Answers
Given:
The dimensions of the square photo are 12'' × 12''.
The frame is 2 inches wider than the photo in both length and width.
To find:
The perimeter of the frame.
Solution:
We have,
Length of the photo = 12 inches
Width of the photo = 12 inches
The frame is 2 inches wider than the photo in both length and width. So,
Length of the frame = 12+2 inches
= 14 inches
Width of the frame = 12 inches
= 14 inches
The perimeter of a square is:
\(P=4a\)
Where, a is the side length.
Now, the perimeter of the square frame with side 14 inches is:
\(P=4(14)\)
\(P=56\)
Therefore, the perimeter of the square frame is 56 inches, Hence, option A is correct.
Please help I have tried so many times and no one helps me please

Answers
Answer:
m(arc)RST = 154 deg
Step-by-step explanation:
Opposite angles of an inscribed quadrilateral are supplementary.
x + 77 + x + 103 = 180
2x + 180 = 180
2x = 0
x = 0
m<RST = x + 77 = 0 + 77 = 77
The measure of an inscribed angle is half the measure of its subtended arc.
m<RST = (1/2)m(arc)RST
77 = (1/2)m(arc)RST
154 = m(arc)RST
m(arc)RST = 154 deg
Find the difference.
(6a^2 − 7− 3a^3) − (7 + a^3 + 2a^2)
(A) −4a^3 + 8a^2 + 14
(B) −2a^3 − 4a^2 − 14
(C) −4a^3 + 4a^2
(D)−4a^3 + 4a^2 − 14
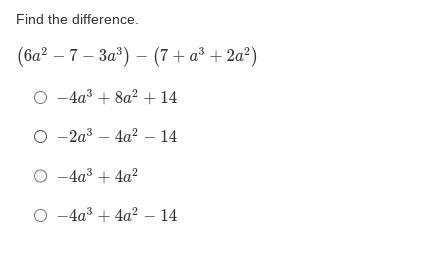
Answers
Combine like terms.
Answer:
4a^2 - 4a^3 - 14
Step-by-step explanation:
Step 1: First, we can distribute the negative to each term in the second expression:
6a^2 - 7 - 3a^3 -7 - a^3 - 2a^2
Step 2: Now we can simplify by combining like terms:
(6a^2 - 2a^2) + (-3a^3 - a^3) + (-7 - 7)
4a^2 - 4a^3 - 14
Thus, the difference of (6a^2 − 7− 3a^3) − (7 + a^3 + 2a^2) is 4a^2 - 4a^3 - 14
Optional Step 3: We can check that we've found the correct difference by plugging in a number for the variable a in both the expression we used to find the difference, (6a^2 − 7− 3a^3) − (7 + a^3 + 2a^2), and the expression we think is the difference, 4a^2 - 4a^3 - 14.
If we get the same value for both when we plug in a, we've correctly found the difference:
Plugging in 2 for a in (6a^2 − 7− 3a^3) − (7 + a^3 + 2a^2):
(6(2)^2 - 7 - 3(2)^3) - (7 + 2^3 + 2(2)^2)
(6 * 4 - 7 - 3 * 8) - (7 + 8 + 2 * 4)
(24 - 7 - 24) - (15 + 8)
(17 - 24) -23
-7 - 23
-30
Plugging in 2 for a in 4a^2 - 4a^3 - 14:
4(2)^2 - 4(2)^3 - 14
4 * 4 - 4 * 8 - 14
16 - 32 - 14
-16 - 14
-30
Thus, we've correctly found the difference of the two expressions
A honeybee population starts with 100 bees and increases at arate of n' (t) bees per week. What does 100 + what does ∫ 15 0 r(t) dt represent?
Answers
The given statement shows that the honeybee population starts with 100 bees and increases at a rate of n'(t) bees per week. However, Adding the initial population (100 bees) to this total increase gives the total honeybee population after 15 weeks.
The population is a function of time, t, so it is denoted by P(t). Thus, the function P(t) represents the honeybee population, where P(0) = 100. What does 100 + what does ∫ 15 0 r(t) dt represent? The following are some definitions and formulas to help you understand the problem better. The rate of change of the population with respect to time is given by the differential equation: dP (t)/dt = n'(t). This equation can be solved using integration to obtain the function P(t). The solution to the differential equation is given by: P(t) = P(0) + ∫ n'(t) dt, where P(0) is the initial population at time t = 0, and n'(t) is the rate of change of the population at time t. The definite integral ∫ 15 0 r(t) dt represents the area under the curve of the function r(t) between the limits t = 0 and t = 15. This area can be interpreted as the total number of bees produced during the first 15 weeks. Therefore, 100 + ∫ 15 0 r(t) dt represents the total population of honeybees after 15 weeks, starting with an initial population of 100 bees.
The expression "100 + ∫ 15 0 r(t) dt" represents the total honeybee population after 15 weeks. The honeybee population starts with 100 bees, and it increases at a rate of n'(t) bees per week. The integral ∫ 15 0 r(t) dt calculates the total increase in the honeybee population over the 15 weeks. Adding the initial population (100 bees) to this total increase gives the total honeybee population after 15 weeks.
Visit here to know more about honeybee population:
brainly.com/question/6357163
#SPJ11
Jim picks a five digit odd number. The second digit is less than 5. The fourth digit is a cube number. The first digit is a prime number. How many different numbers could he pick?
Answers
Answer:
3,000 numbers.
Step-by-step explanation:
First digit: 2, 3, 5, or 7 (primes)
Second digit: 0, 1, 2, 3, or 4 (less than 5)
Third digit: 0-9
Fourth digit: 0, 1, or 8 (cubic numbers)
Fifth digit: 1, 3, 5, 7, or 9 (odd numbers)
So we have 4 * 5 * 10 * 3 * 5 = 3,000 possible numbers.
The height of a ball in feet is modeled by f(x) = -16x² +96x, where x is the time in seconds after it is hit. How long is the ball in the air?
Answers
Answer:
The answer is 144 feet and it will be in the air for 6 sec
Step-by-step explanation:
Answer:
92
Step-by-step explanation:
Like and give 5 star rating
Find the measure of x.
65°
18
x = [?]
Round to the nearest hundredth.
Enter
![Find the measure of x.6518x = [?]Round to the nearest hundredth.Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/3tX2CzUeFotwvl8DqUFLxOvQzlZ0lw5q.png)
Answers
Answer: 585
Step-by-step explanation: You can multiply both numbers and divide by 2 to get the answer
in three flips of an unfair coin the probability of getting three heads is the same as the probability of getting exactly two tails. what is the ratio of the probability of flipping a tail to the probability of flipping a head?
Answers
The ratio of the probability of flipping a tail to the probability of flipping a head when the probability of getting three heads is the same as the probability of getting exactly two tails in three flips is 1/3.
How to find the ratio of probability of flipping a tail to probability of flipping a head?Let p be the probability of flipping a head and q be the probability of flipping a tail.
The probability of getting three heads in three flips is \((p)^3.\)
The probability of getting exactly two tails in three flips is 3pq².
Given that these probabilities are equal, we have:
\((p)^3\)= 3pq²
Simplifying this equation gives:
p = 3q
Dividing both sides by q gives:
p/q = 3
Therefore, the ratio of the probability of flipping a tail to the probability of flipping a head is 1/3.
Learn more about Probability
brainly.com/question/30034780
#SPJ11
Summary
Scatter plots are tools that you can use to display information, and a line of best fit is an instrument that helps to generalize the data in a scatter plot.
When creating a line of best fit, the line should pass through the general area of the data points, but it is not necessary to touch every point. The points should be pretty evenly distributed above and below the line itself.
Answers
Answer:
Hi could you specify the question, I don't see any question in here, else I'd answer it.
Step-by-step explanation:
Which phase best describes the transition from the graph y=2x^2 to the graph of y2x^2+5?
A. 5 units up
B. 5 units down
C. 5 units right
D. 5 units left?

Answers
Answer:
Anything after x determines if it goes up since it's a positive 5 it's 5 units up
Simplify the following using a Property of Integer Exponents.
2,345⁰
Answers
An airplane can seat up to 175 passengers. The airline has already sold 87 tickets for a flight on the airplane. Which graph represents the solution to the inequality that finds the number of tickets the airline can still sell?

Answers
Answer:
C
Step-by-step explanation:
The number of tickets the airline still sells will be 88. Then the correct graph is A.
What is inequality?Inequality is defined as an equation that does not contain an equal sign. Inequality is a term that describes a statement's relative size and can be used to compare these two claims.
An airplane can seat up to 175 passengers.
The airline has already sold 87 tickets for a flight on the airplane.
Then the graph represents the solution to the inequality that the number of tickets the airline still sells will be
Let x be the number of the ticket which need to sell. Then the inequality equation will be
x + 87 ≤ 175
x ≤ 175 - 87
x ≤ 88
Thus, the correct option is A.
More about the inequality link is given below.
https://brainly.com/question/19491153
#SPJ2
an triangle has a angle of 75 degrees, x and y are the missing angles but x is twice y, what are the possibilities of x and y?
Answers
Answer:
x = 70°
y = 35°
Step-by-step explanation:
Given one angle of a triangle is 75° and the other two are 'x' and 'y', you want to find the possible values of 'x' and 'y' when x = 2y.
SetupThe angle sum theorem and the given relation give rise to two equations:
75 +x +y = 180
x = 2y
SolutionUsing the second equation to substitute for x in the first equation, we have ...
75 +(2y) +y = 180
3y = 105 . . . . . . . . . subtract 75 and simplify
y = 105/3 = 35
x = 2y = 2(35) = 70
The measures of angles x and y are 70° and 35°, respectively.
the scale of 1:63,360 is the same as one inch equals ________.
Answers
the answer to the question is one mile
En el mercado del satisfactor X hay 10,000 individuos idénticos, cada uno con una función de demanda definida por Qdx = 12 – Px y 1,000 productores idénticos del satisfactor X, cada uno con una función de oferta dada por Qsx = 20 Px
Answers
Answer:
Px = $4
Step-by-step explanation:
Given that:
En el mercado de satisfacción X hay 10,000 individuos idénticos, cada uno con una función de demanda definida por Qdx = 12 - Px y 1,000 productores idénticos de X satisfactorio, cada uno con una función de oferta dada por Qsx = 20 Px
El precio de equilibrio y la cantidad de equilibrio se pueden determinar de la siguiente manera;
Qdx = 10000(12-Px)
Qdx = 120000 - 10000Px
Qsx = 1000(20 Px)
Qsx = 20000 Px
El punto de equilibrio para completar el enunciado, cuando Qdx = Qsx es:
Qdx = Qsx
120000 - 10000 Px = 20000 Px
120000 = 20000 Px + 10000 Px
120000 = 30000 Px
Px = \(\mathbf{ \dfrac{120000}{30000}}\)
Px = $4
Started at –20° and changed 0° whats is the slope
Answers
Answer:
See below
Step-by-step explanation:
Start out -20 and change 0° ?
then there is zero slope as this would be a horizontal line.
Using the following diagram, determine the values of x, y, and z.
State the solution in simplest radical form or x equals a √b, y = c to the square root d, and z equals e to the square root of f, where a, c, and E are coefficients and become a d, and F are radicants. use NA when necessary

Answers
The values of x, y and z for the right triangle are: x = √6, y = 3, and z = √10 respectively.
How to evaluate the values of x, y, and z for the triangleThe perpendicular height of the right triangle divides the triangle in two triangles with the same proportions as the original triangle.
√15/(y + 2) = y/√15 {opposite/adjacent}
y(y + 2) = (√15)² {cross multiplication}
y² + 2y = 15
y² + 2y - 15 = 0
by factorization;
(y - 3)(y + 5) = 0
y = 3 or y = -5
by Pythagoras rule:
(√15)² = x² + y²
15 = x² + 3²
x = √(15 - 9)
x = √6
z² = (√6)² + 2²
z = √(6 + 4)
z = √10
Therefore, the values of x, y and z for the right triangle are: x = √6, y = 3, and z = √10 respectively.
Read more about right triangle here:https://brainly.com/question/2920412
#SPJ1
Josue wraps a gift box in the shape of a cube. The figure below shows a net for the gift
box.
5-3 cm
How much wrapping paper did he use, in square
centimeters?
Answers
Josue used 150 square centimeters of wrapping paper to cover the cube-shaped gift box
To determine the amount of wrapping paper used by Josue for the cube-shaped gift box, we need to calculate the surface area of the cube.
The net of the gift box consists of six squares, each representing a face of the cube. The dimensions provided in the figure show that each side of the squares is 5 cm.
Since a cube has six faces, we need to calculate the total surface area by multiplying the area of one square face by six.
The formula to find the area of a square is side length squared, so we can calculate the area of one square face as 5 cm * 5 cm = 25 cm².
Now, to find the total surface area, we multiply the area of one face by six: 25 cm² * 6 = 150 cm².
Therefore, Josue used 150 square centimeters of wrapping paper to cover the cube-shaped gift box.
It's worth noting that this calculation assumes that there is no overlap or excess wrapping paper used while wrapping the gift box. Additionally, we have assumed that the dimensions provided are accurate and refer to the side length of the squares in the net.
Overall, the amount of wrapping paper used can vary based on the wrapping technique employed and any additional decorations or folds added to the gift box.
For more question on cube visit:
https://brainly.com/question/1972490
#SPJ8
question 1: is the null hypothesis rejected or not rejected for an observed p-value of at 0.07 at a significance level of 0.05?
Answers
the null hypothesis is rejected for an observed p-value of at 0.07 at a significance level of 0.05.
At a significance level of 0.05, the p-value of 0.07 indicates that the observed value is not statistically significant. As a result, the null hypothesis cannot be disproven.In other words, the observed value is not strong enough to prove that the null hypothesis is false. Therefore, the null hypothesis is not rejected for an observed p-value of 0.07 at the significance level of 0.05.
Learn more about null hypothesis here
https://brainly.com/question/28920252
#SPJ4
How many texts do you send in one day (teenagers) on average? I need this data for a stats lab!!!!
Answers
What is the probability of picking a bottle lid from the jar without looking?
Question
1 of 5
0.4
0.3
Marbles
3
Bottle lids
0.7
4
Stones
3
0.2
Reset
Submit
Answers
Answer:
4.7/10.9
Step-by-step explanation:
In the diagram below, MN is parallel to JK. If JM = 18, MN = 20, and
JK = 32, find the length of ML. Figures are not necessarily drawn to scale. State
your answer in simplest radical form, if necessary.
M
N
K

Answers
Answer:
ML = 30
Step-by-step explanation:
Given the figure:
Where MN is parallel to JK, JM = 18, MN = 20, and JK = 32. We need to find the length of ML.
Since MN and JK are parallel lines, this means that ΔMLN and ΔJLK are similar.
This means that the proportion between the lengths of corresponding sides is constant. In particular, we have:
JK/ MN = JN/ML
From the figure:
32/20 = 18+x / x
we solve the equation for x :
8/5 = 18 + x / x
8x = 5 . 18 + 5x
3x = 90
x = 90/3 = 30
Answer:
ML = 30
Brainliest please :)
A simple interest loan of $6000 has an annual interest rate of 4.4% determine the value of P=$6000R=0.044T=10/12Find the amount of interest paid on this loanCalculate the maturity value of this loan
Answers
Answer:
Explanations:
The formula for calculating the simple interest is expressed as:
\(I=\text{PRT}\)where:
• P is the, principal, = $6,000
,• R is the ,rate, = 0.044
,• Time T = 10/12 years
Substitute the given parameters into the formula
\(\begin{gathered} I=6,000\times0.044\times\frac{10}{12} \\ I=\frac{2640}{12} \\ I=\$220 \end{gathered}\)Hence the amount of interest paid on this loan is $220
Maturity value = Principal + Interest
Maturity value = $6000 + $220
Maturity value = $6,220
Hence the maturity value of this loan is 6,220
Simplify the following and leave your answer in smallest form
1 + 2 + 1
_ _ _
2 3 6
Answers
Answer:
1/59
Step-by-step explanation:
Answer:
1/59
think of it dude
Darren is placing shipping boxes in a storage unit with a floor area of x* + 5x° + x7 _ 20x - 14 square units. Each box has a volume of x3 + 10x2 + 29x + 20 cubic units and can hold a stack of items with a height of x + 5 units.
a. How much floor space will each box cover?
b. What is the maximum number of boxes Darren can place on the floor of the storage unit?
c. Assume Darren places the maximum number of boxes on the floor of the storage unit, with no overlap. How much of the floor space is not covered by a box?
Answers
Answer:
Step-by-step explanation:
a. To find out how much floor space each box will cover, we need to multiply the volume of the box by the height of the stack of items. The volume of the box is x3 + 10x2 + 29x + 20 cubic units and the height of the stack of items is x + 5 units. So the floor space covered by each box is (x3 + 10x2 + 29x + 20) * (x + 5) square units.b. To find the maximum number of boxes Darren can place on the floor of the storage unit, we need to divide the total floor area of the storage unit by the floor space covered by each box. The total floor area of the storage unit is x* + 5x° + x7 _ 20x - 14 square units and the floor space covered by each box is (x3 + 10x2 + 29x + 20) * (x + 5) square units, then we can divide the total floor area by the floor space covered by each boxx* + 5x° + x7 _ 20x - 14 / (x3 + 10x2 + 29x + 20) * (x + 5) = maximum number of boxesc. To find out how much of the floor space is not covered by a box, we can subtract the floor space covered by the maximum number of boxes from the total floor area of the storage unit.Total floor area - floor space covered by the maximum number of boxes = remaining floor space.Please note that this is a polynomial equation and the solution will be different depending on the value of x.
a) Floor space of each box = (\(x^3 + 10x^2 - 29x + 20\)) / (x + 5)
b) Maximum number of boxes = (\(x^4 + 5x^3 + x^2 - 20x - 14\)) / ((\(x^3 + 10x^2 - 29x + 20\)) / (x + 5))
c) Uncovered floor space = \(x^4 + 5x^3 + x^2 - 20x - 14 - ((x^3 + 10x^2 - 29x + 20) / (x + 5) * Maximum number of boxes)\)
We have a storage unit with a given floor area and boxes with specified volumes and heights.
We'll determine the floor space each box covers, the maximum number of boxes Darren can place on the floor, and how much floor space is left uncovered when he places the maximum number of boxes without overlap.
a) Floor space covered by each box:
To find the floor space covered by each box, we divide the volume of the box by its height. This gives us the area each box covers on the floor.
The floor space of each box can be calculated by dividing its volume by its height.
The volume of each box is given by the expression \(x^3 + 10x^2 - 29x + 20\), and its height is x + 5. Therefore, the floor space covered by each box can be represented as:
Floor space of each box = Volume of the box / Height of the box
Floor space of each box = \((x^3 + 10x^2 - 29x + 20) / (x + 5)\)
b) Maximum number of boxes Darren can place:
To find the maximum number of boxes Darren can place on the floor, we need to divide the total floor area by the floor space covered by each box.
The maximum number of boxes Darren can place is determined by dividing the total floor area, given by \(x^4 + 5x^3 + x^2 - 20x - 14\), by the floor space covered by each box. We already calculated the floor space of each box as \((x^3 + 10x^2 - 29x + 20) / (x + 5)\). Now, we'll perform the division:
Maximum number of boxes = Total floor area / Floor space of each box
Maximum number of boxes = \((x^4 + 5x^3 + x^2 - 20x - 14) / ((x^3 + 10x^2 - 29x + 20) / (x + 5))\)
c) Uncovered floor space with maximum number of boxes:
To find the uncovered floor space when Darren places the maximum number of boxes without overlap, we subtract the total floor area covered by the boxes from the total floor area of the storage unit.
The floor space not covered by boxes can be determined by subtracting the total floor area covered by the boxes from the total floor area of the storage unit.
We already know the total floor area of the storage unit is \(x^4 + 5x^3 + x^2 - 20x - 14\), and we calculated the floor space covered by each box in part (a). The maximum number of boxes Darren can place was determined in part (b). Now, we'll perform the subtraction:
Uncovered floor space = Total floor area of storage unit - (Floor space of each box × Maximum number of boxes)
Uncovered floor space =\(x^4 + 5x^3 + x^2 - 20x - 14 - ((x^3 + 10x^2 - 29x + 20) / (x + 5) * Maximum number of boxes)\)
To know more about Volumes here
https://brainly.com/question/31208584
#SPJ2
Complete Question
Darren is placing shipping boxes in a storage unit with a floor area of
\(x^4+5x^3+x^2-20x-14\) square units. Each box has a volume of \(x^3+10x^2-29x+20\).
cubic units and can hold a stack of items with a height of x + 5 units.
a) How much floor space will each box cover?
b) What is the maximum number of boxes Darren can place on the floor of the storage unit?
c) Assume Darren places the maximum number of boxes on the floor of the storage unit, with no overlap. How much of the floor space is not covered by a box?
7. Use the dot product to determine which of the following vector pairs are
orthogonal,
A. v, (22,15) and v₂ = (-2,4)
Part I: Multiply the two x-coordinates of the vectors and the two y
coordinates of the vectors. Write each product below. (2 points)
Answers
The vector pairs v, (22,15) and v₂ = (-2,4) are not orthogonal.
What is vector algebra?Vector algebra entails performing algebraic operations on vectors. Vector algebra performs algebraic operations on vector magnitude and vector direction. Many applications in physics and engineering use vector algebra to perform addition and multiplication operations on physical quantities represented as vectors in three-dimensional space.
Given that the vector pairs are v, (22,15) and v₂ = (-2,4). For the vectors to be orthogonal the dot product should be equal to zero.
Calculate the dot product for the given points,
V = ( 22i + 15j) . ( -2i + 4j )
V = -44 + 60 Here, (i.i =1 and j.j = 1)
V = 16
The dot product is not equal to zero. Hence, the vectors are not orthogonal.
To know more about vector algebra follow
https://brainly.com/question/17173459
#SPJ1
NO LINKS OR FILES JUST THE CORRECT ANSWER

Answers
Answer:a
Step-by-step explanation:
Mr. and Mrs. Happychuck had a healthy baby boy named Chuck who weighed 7.5 pounds at birth. At the end of 4 months, the baby weighed 13.5 pounds. What is Chuck's weight age ratio at 4 months? (Call on a student to answer; the ratio is 13.5 pounds to 4 months or (13.5)/4. It is important to make sure that the students always mention the units involved, in this case pounds and months. Then ask the students to calculate the rate of change of Chuck's weight, that is, how much he gained per month. Ask a volunteer to go to the board and do the work.
PLEASE I NEED HELP! I DESPERATELY NEED ALL OF THE WORK OUT TO THIS PROBLEM< PLEASE
Answers
Answer:
(13.5)/4 = 3.375
step-by-step explanation
the length of the segment between the points $(2a, a-4)$ and $(4, -1)$ is $2\sqrt{10}$ units. what is the product of all possible values for $a$?
Answers
To find the length of the segment between the given points, we can use the distance formula. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
\[d = \sqrt{{(x_2 - x_1)^2 + (y_2 - y_1)^2}}\]
Let's apply this formula to the given points: $(2a, a-4)$ and $(4, -1)$.
The distance between these two points is $2\sqrt{10}$ units. So we have:
\[2\sqrt{10} = \sqrt{{(4 - 2a)^2 + (-1 - (a-4))^2}}\]
Simplifying the equation, we get:
\[4\sqrt{10} = \sqrt{{(4 - 2a)^2 + (-5 - a)^2}}\]
Squaring both sides of the equation, we have:
\[160 = (4 - 2a)^2 + (-5 - a)^2\]
Expanding the equation, we get:
\[160 = 16 - 16a + 4a^2 + 25 + 10a + a^2\]
Combining like terms, we have:
\[0 = 5a^2 - 6a + 1\]
Now, we can solve this quadratic equation for the possible values of $a$.
Factoring the equation, we have:
\[0 = (5a - 1)(a - 1)\]
Setting each factor equal to zero and solving for $a$, we get:
\[5a - 1 = 0 \quad \Rightarrow \quad a = \frac{1}{5}\]
\[a - 1 = 0 \quad \Rightarrow \quad a = 1\]
Therefore, the possible values for $a$ are $\frac{1}{5}$ and $1$. The product of these values is:
\[\left(\frac{1}{5}\right) \cdot 1 = \frac{1}{5}\]
So, the product of all possible values for $a$ is $\frac{1}{5}$.
Learn more about distance formula here : brainly.com/question/25841655
#SPJ11
Solve for x:
-4x+1`=-9x+16
Answers
Answer:
zxc
Step-by-step explanation:
xzcsdcasc
Answer:
x=3
Step-by-step explanation:
−4x+1+9x=−9x+16+9x
5x+1=16
Step 2: Subtract 1 from both sides.
5x+1−1=16−1
5x=15
Step 3: Divide both sides by 5.
5x/5 =15/5
x=3