Find -6/7÷3/14 Write in simplest form
Answers
Answer:
-4
Step-by-step explanation:
(-6/7) / (3/14)
-0.8571428571 / 0.2142857143
-4
\(\huge\pink{\mathbb{Answer:}}\)
The simplest form of
\( \frac{ - 6}{7} \: \div \frac{3}{4} \)
is
\(-4\)
\(\huge\color{purple}{ \colorbox{orange}{\colorbox{white} {ChaEunWoo2009}}}\)
#CarryOnLearning
Related Questions
i really need help, please dont put something silly.

Answers
Answer:
1) 2.92405063291 (put it in the correct amount of significant figures)
2) 6.4688 (put it in the correct amount of significant figures)
Step-by-step explanation:
i dont know how many significant figures to put it into but theres the full answers
A line passes through the points (8,5) and (4,4). What is its equation im slope-intercept from?
Answers
Given the points ( 8 , 5 ) and ( 4 , 4 )
The general slop-intercept form of the equation of the line is:
y = mx + c
where m is the slope and c is y-intercept
The slope will be calculated as following:
\(\text{slope}=m=\frac{y2-y1}{x2-x1}=\frac{5-4}{8-4}=\frac{1}{4}\)So, the equation of the line will be:
\(y=\frac{1}{4}x+c\)Using the one of the given points to find the value of c
Let , we will use the point ( 4 , 4 )
so, when x = 4 , y = 4
\(\begin{gathered} 4=\frac{1}{4}\cdot4+c \\ 4=1+c \\ c=4-1=3 \end{gathered}\)So, the slope - intercept equation of the line is:
\(y=\frac{1}{4}x+3\)Express 40% as a decimal number
Answers
Answer:.40 or .4 would be the correct answer
Answer:
0.4
Step-by-step explanation:
40% can be written as 0.4. Recall that to get a decimal to a percent or vice versa, you can move the decimal place 2 places to the right or left to get the desired outcome. In this case, the decimal needs to move 2 places to the left leaving you with the decimal 0.4 or 4 parts out of 10 (40 parts out of 100= 40%)
help me becasue i do not know the answers to this
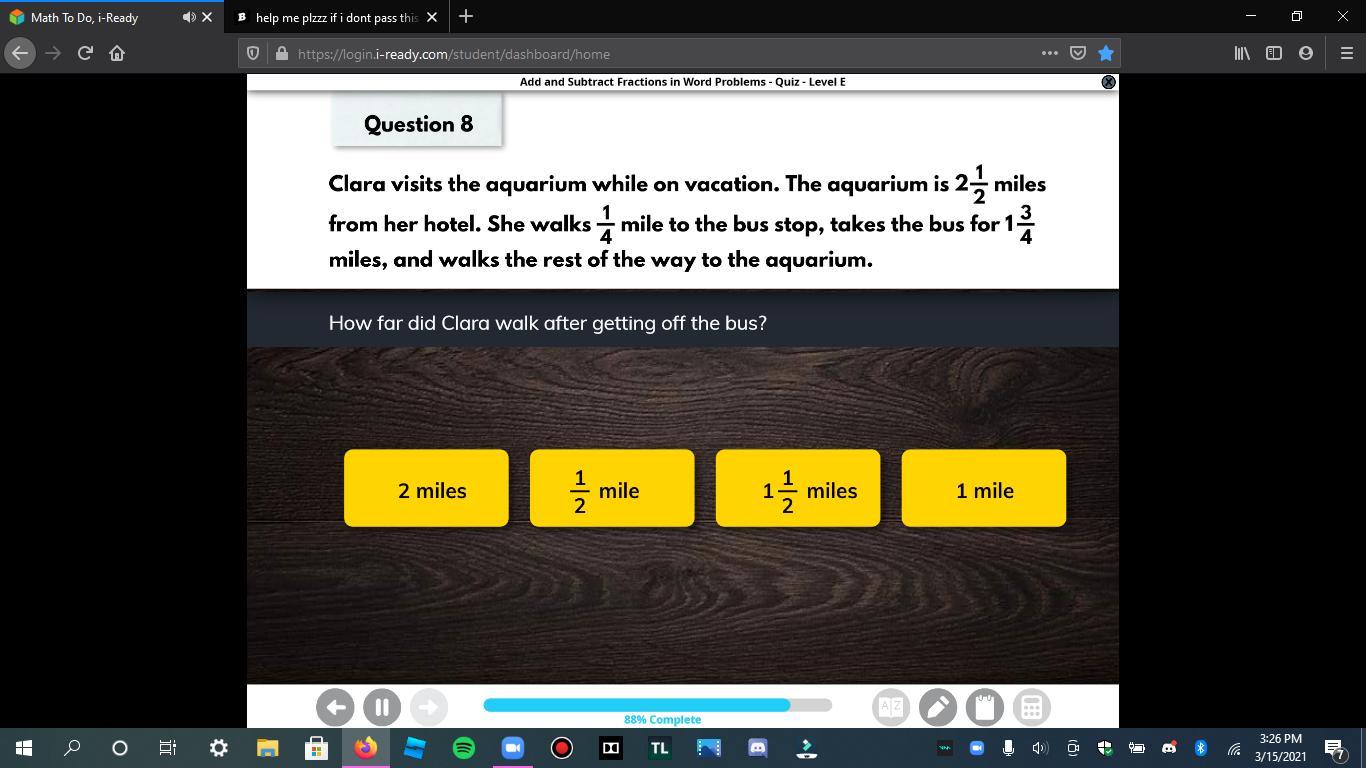
Answers
3. Find \( y^{\prime} \) for the following implicit function \( y^{2}-x^{2} y=-2 \)
Answers
The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).
To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:
Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:
\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)
Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:
\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)
Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.
So, the differentiation of the entire equation is:
\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)
Now, let's rearrange the terms:
\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)
Simplifying further:
\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)
Factoring out:
\(\[(\frac{dy}{dx})(y - x) = 0 \]\)
Finally, solving:
\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)
Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.
Learn more about derivative
brainly.com/question/29144258
#SPJ11
1. Find the derivative: y=log4 (5x³) + 73x² - cos(4x)sin-¹ (3x² + 2x) 2-5. Differentiate: 1²-161
Answers
The derivative of y = log₄(5x³) + 73x² - cos(4x)sin⁻¹(3x² + 2x)²⁻⁵ is given by:
dy/dx = (3/ln(4))x²/((5x³)ln(4)) + 146x - (-sin(4x))/(√(1 - (3x² + 2x)²))²⁻⁵.
To find the derivative of the given function, we apply the chain rule and the derivative rules for logarithmic, trigonometric, and inverse trigonometric functions.
Let's break down the derivative step-by-step:
1. For the first term, y = log₄(5x³), we use the chain rule and the derivative of the natural logarithm:
dy/dx = (1/ln(4))(d/dx)(5x³) = (1/ln(4))(15x²).
2. For the second term, y = 73x², the derivative is simply 146x, as the exponent ² comes down as a coefficient.
3. For the third term, y = cos(4x)sin⁻¹(3x² + 2x)²⁻⁵, we apply the chain rule and the derivatives of cosine and inverse sine:
dy/dx = -sin(4x)(d/dx)[sin⁻¹(3x² + 2x)²⁻⁵].
Using the chain rule, we get:
dy/dx = -sin(4x)(-cos⁻¹(3x² + 2x)²⁻⁵)(d/dx)[(3x² + 2x)²⁻⁵].
Further simplifying, we have:
dy/dx = -sin(4x)(-cos⁻¹(3x² + 2x)²⁻⁵)((-10x - 2)(3x² + 2x)²⁻⁶).
Combining all the derivative terms, we obtain the final expression:
dy/dx = (3/ln(4))x²/((5x³)ln(4)) + 146x - (-sin(4x))/(√(1 - (3x² + 2x)²))²⁻⁵.
Therefore, the derivative of the given function is (3/ln(4))x²/((5x³)ln(4)) + 146x - (-sin(4x))/(√(1 - (3x² + 2x)²))²⁻⁵.
Learn more about derivative here:
https://brainly.com/question/29144258
#SPJ11
The times taken by Amal to run three races were 3 minutes 10 seconds, 2 minutes 58.2 seconds and 3 minutes 9.8 seconds. Find the average time taken, giving your answer in minutes.
Answers
Approximately it is:
3 minutes 19 seconds
use the result from part (a) to determine a solution of the linear system ax = b. does the system have any other solutions? explain
Answers
The determine a solution of the linear system ax = b, we can use the result from part (a) and plug it into the equation. To determine if the system has any other solutions, we can look at the determinant of the system.
the linear system ax = b can have other solutions. To determine any other solutions, you must use the result from part (a) to solve for x, then add any multiple of the column vector for the coefficient matrix A. This is because if ax = b, then (A + kA)x = b + kb, and thus the new system (A + kA)x = b + kb has the same solutions as the original system ax = b.
To determine a solution of the linear system ax = b, we can use the result from part (a) and plug it into the equation. This will give us the value of x that satisfies the equation.
For example, if the result from part (a) is 2, we can plug it into the equation ax = b to get 2a = b. We can then solve for a to get a = b/2. This is one solution of the linear system.
To determine if the system has any other solutions, we can look at the determinant of the system. If the determinant is nonzero, then the system has a unique solution. If the determinant is zero, then the system has either no solutions or infinitely many solutions.
In this case, if the determinant is nonzero, then the system has only one solution, which is the one we found earlier. If the determinant is zero, then we need to look at the system further to determine if it has no solutions or infinitely many solutions.
Overall, to determine a solution of the linear system ax = b, we can use the result from part (a) and plug it into the equation. To determine if the system has any other solutions, we can look at the determinant of the system.
Learn more about Determine
brainly.com/question/13369636
#SPJ11
Mr. Campos loves to buy a bucket of popcorn when he goes to Disneyland. Complete the table in your notes to determine how much buckets of popcorn at the following intervals cost's.

Answers
3: 5/47.5
4: 12/114
:) hope this helps
can someone please help meeee?
Answers
In problems 1-3 find all prime ideals and maximal ideals in the given ring.
1. 26 2. Z18 3.) Z2 X Z8
Answers
In the case of direct products, the prime/maximal ideals are formed by taking the corresponding prime/maximal ideals from each factor of the direct product.
How to find all prime ideals and maximal ideals in the given rings?To find all prime ideals and maximal ideals in the given rings, let's analyze each case:
Ring: Z/26Z (the ring of integers modulo 26)
To find the prime ideals in this ring, we need to consider the ideals that are prime. In Z/26Z, the prime ideals correspond to the prime numbers in Z that divide 26.
Prime ideals: (2), (3), (13)
To find the maximal ideals, we need to consider the maximal proper ideals in Z/26Z.
Maximal ideals: (2), (13)
Ring: Z/18Z (the ring of integers modulo 18)
Prime ideals: (2), (3)
Maximal ideals: (2)
Ring: Z/2Z x Z/8Z (the direct product of the rings Z/2Z and Z/8Z)
Prime ideals: (0) x (2), (1) x (8), (1) x (2)
Maximal ideals: (1) x (8), (1) x (2)
In the case of direct products, the prime/maximal ideals are formed by taking the corresponding prime/maximal ideals from each factor of the direct product.
Learn more about Prime and maximal
brainly.com/question/30968517
#SPJ11
If 4 dozens eggs cost 336 pesos , then the cost of each egg is ?
Answers
Answer:
Each egg is 7 pesos
-------------------------------------------------------------------------------------------------------------
Step-by-step explanation:
One dozen mean 12, so 4 dozens means 4 x 12 = 48.
Dividing 336 by 48 we get
336 ÷ 48
= 7
Hence, the cost for each egg is 7 pesos.
-------------------------------------------------------------------------------------------------------------
Hope this helps :)
Have a nice day!
The sum of the measures of the angles of a triangle is 180 m

Answers
The sum of the measures of the angle of a triangle is 180 degrees.
Sum of angles in a triangleThe given triangle is a type of triangle and the type of triangle a scalene triangle.
For a scalene triangle, the measure of the three sides are unequal and the sum of the interior angle of a triangle is 180 degrees.
Hence the measure of the angles <A, <B and <C are all less than 90 degrees since they are all acute angles.
We can therefore conclude that:
m<A + m<B + m<C = 180 degrees
Learn more on triangle sum theorem here: https://brainly.com/question/30870203
#SPJ1
help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
Help
PLEASE!!!!!!!
Plz
Help
Help
Answers
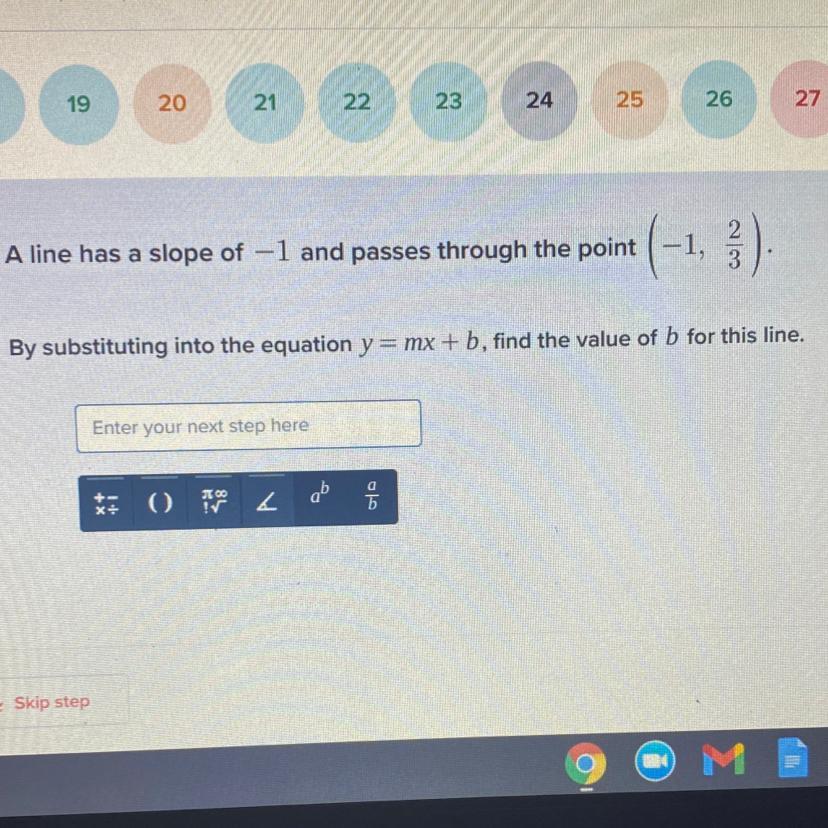
Step-by-step explanation:
y = mx + b
\( \frac{2}{3} = ( - 1)( - 1) + b\)
\( \frac{2}{3} - 1 = b\)
\( \frac{2}{3} - \frac{3}{3} = b\)
\( - \frac{1}{3} = b\)
Answer:
The next step would be to multiply your slope by your x value.
Step-by-step explanation:
The overall answer would is b=-1/3
BTW...if y'all have any questions for school (it can be any grade level or subject) just comment here and I will get to it as soon as I can!! ❤
Answer all please I need this :o

Answers
Answer:
18. d
19. c (not sure)
20. c
Answer:
18) d. Synopsis
19) c. Duration
20) c. Pacify
Step-by-step explanation:
18) When you don’t wanna give the full version of a story sum it up; give a summary or synopsis!
19) Uh tbh it just makes the most sense in context of the sentence, read it all together and you’ll see ;)
20) In the sentence it says “calm down” only way to calm someone down is to pacify them or give them what they want… in this context she needs to pacify them. Plus it just makes sense.
Hope this helps, good luck have a good day!
Based on the figure below. A force D intersect the x-axis between point C and 2.3 m from point B. If the moments at points A and B are 181 N-m counterclockwise and 50 N-m clockwise respectively. Find the distance in meters of the y-intercept of force D from point C.
Answers
The distance in meters of the y-intercept of force D from point C ,c = d - 2.3 m.
To solve for the distance 'd', another equation. Since force D intersects the x-axis between point C and 2.3 m from point B, it means that the distance 'd' is equal to the distance between point C and the y-axis, which is represented by 'c'.
Two unknowns 'd' and 'F', but another equation using the principle of moments at point C.
Moment at point C = 0 (in equilibrium)
The moment at point C is clockwise and is given by:
Moment at C = F × (2.3 m - d + c) = 0
Simplifying the equation,
2.3 m - d + c = 0
Rearranging the equation,
c = d - 2.3 m
Now, we have two equations:
F × (2.3 m - d) = 131 N-m (Equation 1)
To know more about distance here
https://brainly.com/question/31713805
#SPJ4
Need help and fast please and thank you.
y= 0.141(15) + 0.842 =
Answers
y = 2.115 + 0.842
= 2.957
no explanation
Haley and Ryan are finding 7 – 3 + 2. Who is correct? Explain your answer.

Answers
Answer:
I think that the person who is right is Ryan because he used the all the proprieties in the right way
Step-by-step explanation:
Answer: Ryan's work is correct because if you Subtract 7 and 3 you would get 4. Then you add 2 you would get 6.
Step-by-step explanation: Step 1: (7 - 3 = 4) Step 2: (4 + 2 = 6)
Here is a pyramid with a base that is a pentagon with all sides the same length.
a. Describe the cross section that will result if the pyramid is sliced:
horizontally (parallel to the base)
vertically through the top vertex (perpendicular to the base).
b. Describe another way you could slice the pyramid that would result in a different cross section.
Answers
a) If sliced horizontally, the cross section will be a regular pentagon. If sliced vertically, the cross section will be an isosceles triangle. b) By cutting it diagonally from one corner of the pentagon base to the opposite corner.
a. If the pyramid is sliced horizontally, parallel to the base, the resulting cross section will be a regular pentagon. The shape will have the same number of sides as the base of the pyramid, and each side will have the same length.
If the pyramid is sliced vertically through the top vertex, perpendicular to the base, the resulting cross section will be an isosceles triangle. The triangle will have one side that is the height of the pyramid and two sides that are equal in length. The base of the triangle will be the same as the side length of the pentagon base of the pyramid.
b. Another way to slice the pyramid that would result in a different cross section is by cutting it diagonally from one corner of the pentagon base to the opposite corner. This diagonal slice would create a cross section that is a trapezoid. The trapezoid will have one pair of parallel sides (the bases), and the other two sides will be slanted. The length of the slanted sides will depend on the angle and position of the slice relative to the base.
To learn more about pentagon here:
https://brainly.com/question/11856530
#SPJ4
Let S = {0, 1, { 0, {1} } and let T = {0, {∅, {∅} }
How many function f : S → T are injective =
How many function f : T → S are surjective =
How many function f : T → S are invertible =
Given each of the following sets in list notation.
S ∪ T =.
S − T =.
Answers
The number of injective functions f: S → T is 4. The number of surjective functions f: T → S is 8. There are no invertible functions f: T → S. S ∪ T = {0, 1, {0, {1}}, ∅, {∅}}. S − T = {1, {0, {1}}}.
To determine the number of injective functions f: S → T, we need to count the number of ways to assign distinct elements of T to the elements of S. Since S has 3 elements and T has 4 elements, we have 4 choices for f(0), 3 choices for f(1), and 2 choices for f({0, {1}}). Therefore, the total number of injective functions is 4 × 3 × 2 = 24. However, we need to account for the fact that f({0, {1}}) can be assigned to either {∅} or {∅, {∅}}. So, we divide the total by 2 to get 24 / 2 = 12. But there are two injective functions that map everything to ∅, so the final count is 12 - 2 = 10.
To count the number of surjective functions f: T → S, we need to determine how many ways each element of T can be mapped to an element of S. The element 0 can be mapped to any of the three elements in S, and the element {∅, {∅}} must be mapped to {0, {1}}. So, we have 3 choices for f(0) and 1 choice for f({∅, {∅}}). Therefore, the total number of surjective functions is 3 × 1 = 3.
For a function to be invertible, it must be both injective and surjective. Since we have found that there are no invertible functions f: T → S (as there are no surjective functions in this case), the count is 0.
The union of sets S and T, denoted as S ∪ T, is the set that contains all elements from both S and T without duplication. Therefore, S ∪ T = {0, 1, {0, {1}}, ∅, {∅}}. The set difference S − T is the set of elements that are in S but not in T. Therefore, S − T = {1, {0, {1}}}.
LEARN MORE ABOUT functions here: brainly.com/question/32706318
#SPJ11
Sorry but what is “ 6(-5n + 7) “ equal ?
Answers
Answer:
-30n+42
Step-by-step explanation:
6(−5n+7)
=(6)(−5n+7)
=(6)(−5n)+(6)(7)
=−30n+42
Answer: − 30 n + 42
Step-by-step explanation:
what is .7 of a mile
Answers
Answer:
1232 yards or 3696 feet or 44352 inches or 0.7 of a mile
Step-by-step explanation:
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
a ball is dropped from a height of 6 ft. assuming that on each bounce, the ball rebounds to one-third of its previous height, find the total distance traveled by the ball.
Answers
A ball is dropped from a height of 6 ft. assuming that on each bounce, the ball rebounds to one-third of its previous height, the total distance traveled by the ball is approximately 11.926 feet.
How do we calculate the total distance?We have to calculate the distance traveled by the ball with the help of the given data, as shown below;The first height of the ball is 6 feet. Distance traveled by the ball at the first instance = 6 feet.The ball rebounds to one-third of its previous height, and the ball goes to a height of:6/3 = 2 feet.
Distance traveled by the ball after the first bounce = 6 + 2 + 2 = 10 feet.The ball rebounds again to one-third of its previous height, and the ball goes to a height of:2/3 = 0.6667 feet. Distance traveled by the ball after the second bounce = 10 + 0.6667 + 0.6667 = 11.3334 feet.
The ball rebounds again to one-third of its previous height, and the ball goes to a height of:0.6667/3 = 0.2222 feet. Distance traveled by the ball after the third bounce = 11.3334 + 0.2222 + 0.2222 = 11.7778 feet. The ball rebounds again to one-third of its previous height, and the ball goes to a height of:0.2222/3 = 0.0741 feet.
Distance traveled by the ball after the fourth bounce = 11.7778 + 0.0741 + 0.0741 = 11.926 feet. Therefore, the total distance traveled by the ball is approximately 11.926 feet.
See more about total distance at: https://brainly.com/question/29409777
#SPJ11
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 7 g(x) = { vt ++3 dt Jo Answer 8. g(x) = {* In (1+tº) dt
Answers
By using Fundamental Theorem of Calculus, we find the derivative of the function g(x) = In { sqrt( t + t^3)dt } limit from x to 0 is ln(sqrt(x + x^3)). The derivative of the function g(x) = { In (1+t^2) dt} where limit are from x to 1 is ln(1 + x^2).
The Fundamental Theorem of Calculus, which states that if a function is defined as the definite integral of another function, then its derivative is equal to the integrand evaluated at the upper limit of integration.
So, applying this theorem, we have:
g'(x) = d/dx [∫x_0 ln(sqrt(t + t^3)) dt]
= ln(sqrt(x + x^3)) * d/dx (x) - ln(sqrt(0 + 0^3)) * d/dx (0)
= ln(sqrt(x + x^3))
Therefore, g'(x) = ln(sqrt(x + x^3)).
Using the Fundamental Theorem of Calculus, we have:
g'(x) = d/dx [∫1_x ln(1 + t^2) dt]
= ln(1 + x^2) * d/dx (x) - ln(1 + 1^2) * d/dx (1)
= ln(1 + x^2)
Therefore, g'(x) = ln(1 + x^2).
To know more about Fundamental Theorem of Calculus:
https://brainly.com/question/30761130
#SPJ4
____The given question is incomplete, the complete question is given below:
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 7 g(x) = In { sqrt( t + t^3)dt } limit from x to 0. 8. g(x) = { In (1+t^2) dt} where limit are from x to 1.
Your teacher asks you to find a recipe that includes two ingredients with a ratio of 1/2 over one 1/8 cup . Give an example of two ingredients in a recipe that would meet this requirement
Answers
The recipe of flour and sugar can be given as an example where we will get the ratio as 4 : 1.
The example is with flour and sugar
Let
x = the number of cups of flour
y = the number of cups of sugar
We know that:
Ratio means the comparison between the two values.
Ratio = x / y
Now, we can let
x = 1 / 2 cups of flour
y = 1 / 8 cups of sugar
Ratio will be
= 1 / 2 : 1 / 8
= 8 : 2
= 4 : 1
Therefore, the recipe of flour and sugar can be given as an example where we will get the ratio as 4 : 1.
Learn more about ratio here:
https://brainly.com/question/2328454
#SPJ9
On the unit circle, where 0 < theta < or equal to 2pi, when is tan theta undefined?
A. Theta=pi and theta=2pi
B. sin theta = cos theta
C. theta = pi/2 and theta=3pi/2
D. sin theta = 1/cos theta
Answers
Therefore, the answer is option C: theta = pi/2 and theta = 3pi/2.
To determine when tan(theta) is undefined on the unit circle, we need to remember the definition of the tangent function.
Tangent is defined as the ratio of the sine and cosine of an angle. Specifically, tan(theta) = sin(theta)/cos(theta).
Now, we know that cosine can never be equal to zero on the unit circle, since it represents the x-coordinate of a point on the circle and the circle never crosses the x-axis. Therefore, the only way for tan(theta) to be undefined is if the cosine of theta is equal to zero.
There are two values of theta on the unit circle where cosine is equal to zero: pi/2 and 3pi/2.
At theta = pi/2, we have cos(pi/2) = 0, which means that tan(pi/2) = sin(pi/2)/cos(pi/2) is undefined.
Similarly, at theta = 3pi/2, we have cos(3pi/2) = 0, which means that tan(3pi/2) = sin(3pi/2)/cos(3pi/2) is also undefined.
Therefore, the answer is option C: theta = pi/2 and theta = 3pi/2.
To know more about theta visit:-
https://brainly.com/question/21807202
#SPJ11
what is the answer to this math problem(-2.7)(-1.9)
Answers
Answer:
-5.13
Step-by-step explanation:
now we can say that h(z) is a constant k, and so, taking k = 0, a potential function is f(x, y, z) =
Answers
If we say that h(z) is a constant k and k = 0, the potential function f(x, y, z) is g(x, y)
Here, g(x, y) is a function of the variables x and y, and has no dependence on z.
What makes a function?A function is a way two sets of values are linked: the input and the output. The function tells us what output value corresponds to each input value.
In function, each input has only one output, so it's like a rule that tells us exactly what to do with the input to get the output.
This rule can be written using Mathematical expressions, formulas, or algorithms to follow.
Learn more about expressions at brainly.com/question/1859113
#SPJ1
AB = 2x + 3, BC = 3x + 7, AC = 60. what does x represent
Answers
Answer:
AC=AB+BC
60=2x+3+3x+7
60=2x+3x+3+7
60=5x+10
60-10=5x
50=5x
x=10