FAST
Choose the best description for the real number 4.6 with a repeating 6. (4 points)
Irrational, because it is a terminating decimal
Irrational, because it is a repeating decimal
Rational, because it is a terminating decimal
Rational, because it is a repeating decimal
Answers
Answer:
Rational, because it is a repeating decimal
Step-by-step explanation:
i go a 20/20 on mine
Related Questions
I need help and I’ll give 100 points

Answers
Answer:
the student may have made the mistake because the student was paying more attention to how many blocks he was filling in rather than how much he was filling in.
to solve the problem correctly you would just switch the decimals
0.8 > 0.08
0.8 should have 80 blocks filled
0.08 should have 8 blocks filled
Decide which of the two points lies on the graph of the line
2x+y=10
A.(4,3)
B.(-4,18)
Answers
Answer:
A
Step-by-step explanation:
when you substitute 4 in x and 3 in y, your result are 11 no 10
help with this question

Answers
Answer:
Of members(2) and of phone conversation (1) cuz they had two people and you had to call 1 at a time ☺
In rhombus WXYZ, if WX=15, find YZ.
Answers
Answer:
YZ=15
Step-by-step explanation:
All sides of a rhombus are equal so it would be the same length.
ple Interes How much simple interest would be earned on a savings account of $4,500 at 5.5% interest per year after 24 months? I=(4,500)(055)(2)
Answers
4500(1+0.055)^24
4500(1.055)^24
= 16,265.65456755
For each f ∈ C[0,1], define L(f)=F, where
(not sure how to put integral sign in)
F(x) = (integral from 0-X) f (t) dt 0 ≤ x ≤ 1
Show that L is a linear operator on C [0, 1] and then
find L(ex ) and L(x2).
Answers
For each f ∈ C[0,1], where F(x) = ∫₀ˣf(t) dt, then the proof that "L" is a linear operator on C [0, 1] is shown below, and the value of L(eˣ) = eˣ - 1 and L(x²) = x³/3.
In order to show that L is a "linear-operator" on C[0,1], we need to prove that : L(cf) = cL(f) for any scalar c, and
L(f + g) = L(f) + L(g) for any f,g ∈ C[0,1]
Proof : L(cf)(x) = ∫₀ˣ cf(t) dt = c ∫₀ˣ f(t) dt = cL(f)(x), thus L is linear with respect to scalar multiplication.
⇒ L(f+g)(x) = ∫₀ˣ (f(t) + g(t)) dt = ∫₀ˣ f(t) dt + ∫₀ˣ g(t) dt = L(f)(x) + L(g)(x), thus L is linear with respect to addition.
Now, we find L(eˣ) and L(x²) using the definition of L:
L(eˣ)(x) = ∫₀ˣ \(e^{t}\) dt = eˣ - 1, and
L(x²)(x) = ∫₀ˣ t² dt = x³/3.
Therefore, L(eˣ) = eˣ - 1 and L(x²) = x³/3.
Learn more about Linear Operator here
https://brainly.com/question/31438437
#SPJ4
The given question is incomplete, the complete question is
For each f ∈ C[0,1], define L(f)=F, where
F(x) = (integral from 0-X) f(t) dt 0 ≤ x ≤ 1
Show that L is a linear operator on C [0, 1] and then
find L(eˣ) and L(x²).
Circle T has diameters RP and QS. The measure of ∠RTQ is 12° less than the measure of ∠RTS. What is the measure of ? a.78° b.84° c.88° d.96°
Answers
Answer: The measure of ∠RTS is 102°. The answer is (d).
Step-by-step explanation:
We know that the sum of the angles in a quadrilateral is 360°. Therefore, we have:
∠R + ∠T + ∠Q + ∠S = 360°
Since RP and QS are diameters, we have ∠R = ∠P = 90° and ∠Q = ∠S = 90°. Substituting these values, we get:
90° + ∠T + 90° + ∠S = 360°
Simplifying the equation, we get:
∠T + ∠S = 180°
Now we use the fact that the measure of ∠RTQ is 12° less than the measure of ∠RTS, which can be written as:
∠RTQ = ∠RTS - 12°
Substituting this into the equation above, we get:
∠T + ∠RTS - 12° = 180°
Simplifying, we get:
∠T + ∠RTS = 192°
We can now solve for ∠RTS by substituting ∠T + ∠S = 180° into the equation above:
∠RTS = 192° - ∠T
Substituting this into the equation for ∠RTQ above, we get:
∠RTQ = (192° - ∠T) - 12° = 180° - ∠T
Since the sum of the angles in triangle RTQ is 180°, we have:
∠RTQ + ∠T + ∠R = 180°
Substituting the values for ∠R and ∠RTQ, we get:
90° + ∠T + (180° - ∠T) = 180°
Simplifying, we get:
∠T = 90°
Substituting this value into the equation for ∠RTS above, we get:
∠RTS = 192° - ∠T = 102°
Therefore, the measure of ∠RTS is 102°. The answer is (d).
To know more about quadrilateral refer here
https://brainly.com/question/29934440#
#SPJ11
7b - 9b + 3 + 4b
what is the answer to this problem
Answers
2b + 3
Step-by-step explanation:
Combine like terms
7b -9b = -2b
-2b +4b =2b
2b +3 = 2b+3
The clock has a diameter of 22 inches. What is the circumference of the clock?
Answers
Answer:
The circumference is 44
Answer:
34.56
Step-by-step explanation:
C = 2πr = 2 · π · 5.5 ≈ 34.55752
(score for question 3: ... of 10 points) 3. the table shows the test scores and the sleep averages of several students. test score (%) 88 75 76 92 96 94 83 90 99 65 7788 82 83 94 97 7 6.5 average sleep (h) 6 7.5 8 7 6.5 8 8.5 5 7 8 9 9 9 8.5 8.5 (a) write the least squares regression equation that models the data. let x = the test score and y = average sleep. (b) use the equation to determine the approximate test score of a student who sleeps an average of 8 hours a night. show your work. answer: 1
Answers
The linear regression model obtained by fitting the data points is Y = 0.0914X1 - 0.3741.
How to illustrate the regression?x = test score
y = average sleep
Slope = 0.0914
intercept = - 0.3741
The test score of a student that sleeps 8 hours
y = 8
8 = 0.0914X1 - 0.3741
8 + 0.3741 = 0.0914X1
X = 8.3741 / 0.0914
X = 91.62
Learn more about regression on:
https://brainly.com/question/23884348
#SPJ1
Put the following statements into order to prove that the modus ponens is a valid argument form Not all steps are correct or belong in the proof: Enter N for such steps:
~p V -(p = q) Vq = (Tp Vq) v-(Tp V q)
Answers
The correct order of statements to prove that modus ponens is a valid argument form is as follows: ~p V -(p = q) V q = (Tp V q) v -(Tp V q).
To prove the validity of the modus ponens argument form, we need to arrange the statements in the correct order. Here is the correct order of statements:
~p V -(p = q) V q (Given statement)-(p = q) V ~p V q (Commuted the disjunction)-(p = q) V (Tp V q) (Logical equivalence between ~p and Tp)(p = q) -> (Tp V q) (Implication of the previous statement)(Tp V q) v -(Tp V q) (Law of excluded middle)The first statement is given, and we begin by commuting the disjunction in the second statement. Then, we use the logical equivalence between ~p and Tp to rewrite the third statement. This allows us to express the conditional statement (p = q) -> (Tp V q) in the fourth statement. Finally, we apply the law of excluded middle in the last statement.
It's important to note that the correctness of each step has not been explicitly specified, so we assume that all the steps in the proof are correct and belong to the final valid argument form.
Learn more about statements here:
https://brainly.com/question/32882764
#SPJ11
Find the absolute extrema for the given function on the interval [15.6, 19.2). Write your answer in the form (x.f(x)). Round your answers to two decimal places. f(x) = In (12x^2 - 11x + 2)
Absolute Minimum: Absolute Maximum
Answers
the absolute extrema of the linear equation f(x) = 12x^2 -11x +2 are 27 (absolute maximum) for x = - 8 and - 9 (absolute minimum) for x = 4. (- 8, 27) and (4, - 9).
What are the absolute extrema of a linear equation within a closed interval?
According to the functions theory, linear equations have no absolute extrema for all real numbers, but things are different for any closed interval as absolute extrema are the ends of linear function. Now we proceed to evaluate the function at each point:
Absolute maximum
f(- 8) = 12x^2 -11x +2
f(- 8) = 27
Absolute minimum
f(4) = - 3 · 4 + 3
f(4) = - 9
By means of functions theory and the characteristics of linear equations, the absolute extrema of the linear equation f(x) = 12x^2 -11x+2 are 27 (absolute maximum) for x = - 8 and - 9 (absolute minimum) for x = 4. (- 8, 27) and (4, - 9).
To learn more on absolute extrema:
brainly.com/question/2272467
#SPJ4
Find the particular antiderivative of the following derivative that satisfies the given condition. C''(x)=4x2-3x ; C(0)=2000
Answers
The particular antiderivative that satisfies the given condition is: C(x) = (4/9)x^4 - (9/8)x^3 + K1x + 2000
To find the particular antiderivative (or integral) of the given derivative \(C''(x) = 4x^2 - 3x\) that satisfies the condition C(0) = 2000, we need to integrate the given function twice.
First, we integrate C''(x) to find C'(x):
\(C'(x) = ∫ (4x^2 - 3x) dx\)
To find the antiderivative of \(4x^2\), we use the power rule for integration: the power of x increases by 1 and is divided by the new power. Similarly, the antiderivative of -3x is \(-(3/2)x^2\).
\(C'(x) = ∫ (4x^2 - 3x) dx = (4/3)x^3 - (3/2)x^2 + K1\)
Here, K1 is the constant of integration. Next, we integrate C'(x) to find C(x):
\(C(x) = ∫ (C'(x)) dx = ∫ ((4/3)x^3 - (3/2)x^2 + K1) dx\)
To find the antiderivative of \((4/3)x^3\), we again use the power rule for integration. Similarly, the antiderivative of \(-(3/2)x^2\) is \(-(3/2)(1/3)x^3\).
The constant of integration K1 will also be integrated with respect to x, resulting in another constant of integration, K2.
\(C(x) = (1/3)(4/3)x^4 - (1/2)(3/2)x^3 + K1x + K2\)
Simplifying further, we have:
\(C(x) = (4/9)x^4 - (9/8)x^3 + K1x + K2\)
Now, we can apply the initial condition C(0) = 2000 to find the particular solution for K2:
\(C(0) = (4/9)(0)^4 - (9/8)(0)^3 + K1(0) + K2 = 2000\)
Since all the terms involving x become zero when x = 0, we have:
K2 = 2000
Therefore, the particular antiderivative that satisfies the given condition is: \(C(x) = (4/9)x^4 - (9/8)x^3 + K1x + 2000\)
To know more about antiderivative refer here:
https://brainly.com/question/33243567
#SPJ11
If Colorado Springs, Colorado, has 1.2 times as many days of sunshine as Boston, Massachusetts, how many days of sunshine does each city have if there are a total of 482 days of sunshine between the two in a year?
Answers
Colorado and Boston have 263 and 219 days of sunshine respectively.
What is the solution to the Equation?Let the number of days of sunshine in Colorado is x and the number of days of sunshine in Boston is y.
Total number of days of sunshine=482
Also, the number of days of sunshine in Colorado is 1.2 times the number of days of sunshine in Boston.
So, the equation is formed as follows:
x+y=482 -(1)
The other equation is formed as:
x=1.2y -(2)
Substitute the value x from equation (2) in (1),
1.2y+y=482
2.2y=482
y=482/2.2
y=219
Substitute the value of y in equation (1),
x+219=482
x=482-219
x=263
Learn more about Equations here:
https://brainly.com/question/2972832
#SPJ4
SOLVE FOR X
X/3 + x-1/4 = 2+X
show (or describe every step)
the x-1/4 is ONE fraction, not a variable minus 1/4.
Answers
Answer:
Step-by-step explanation:
Thank you for the note. You show what you want like this.
X/3 + (x - 1)/4 = 2+X Multiply both sides by 12.
\(\frac{12*x}{3} + \frac{12*(x -1)}{4} = 12(x + 2)\)
Now take mini steps.
1. Divide 3 into 12
4x
2. Divide 4 into 12
3(x - 1)
========================
Here's what you have.
4x + 3(x - 1) = 12(x + 2) Remove the brackets.
4x + 3x - 3 = 12x + 24 Combine like terms
7x - 3 = 12x + 24 Subtract 7x from both sides.
- 3 = 12x - 7x +24
-3 = 5x + 24 Subtract 24 from both sides.
-27 = 5x Divide by 5
x = -5.4
What is the value of x? sin(x 37)°=cos(2x 8)° enter your answer in the box. x =
Answers
cos (2x + 8) = sin (x + 37) = cos (90 - x - 37) = cos (53 - x)
Property of the cosine function -->
(
2
x
+
8
)
=
±
(
53
−
x
)
a. 2x + 8 = 53 - x
3x = 45
x
=
15
∘
b. 2x + 8 = - 53 + x
x
=
−
61
∘
For general answers, add
k
360
∘
Check by calculator.
x = 15 --> sin (x + 37) = sin 52 = 0.788
cos (2x + 8) = cos (38) = 0.788. Proved
x = - 61 --> sin (x + 37) = sin (- 24) = - sin 24 = - 0.407
cos (2x + 8) = cos (-122 + 8) = cos (- 114) = - 0.407. Proved
The value of x which saisfies the equation sin(x+37)°=cos(2x+8)° is 135 or 15.
How to convert sine of an angle to some angle of cosine?We can use the fact that:
\(\sin(\theta ^\circ) = \cos(90 - \theta^\circ)\)
to convert the sine to cosine (but the angles won't stay same unless its 45 degrees).
For this case, we're specified the equation sin(x+37)°=cos(2x+8)°.
Converting sine to cosine, we get:
\(\cos(90 - x - 37)^\circ = \cos(2x + 8)^\circ\\\)
Since cosine is a periodic function with period of \(360^\circ\), thus, we get:
\(90 - x - 37= 2x + 8 +360 n\)
where n = an integer (positive, negative, or zero).
or
\(90 - 37 - 8= 3x + 360 n\\\\x = \dfrac{45 - 360n}{3} = 15 - 120n\)
This is the general solution of the considered equation.
Assuming that only principal values (from 0 to 360 degrees) angles are allowed, we need:
\(0 \leq x + 37 \leq 360\\\\and\\\\0 \leq 2x+8 \leq 360\)
The first inequality gives:
\(-37 \leq x \leq 323\)
The second inequality gives:
\(-4 \leq x \leq 176\)
We need to satisfy both the inequalities, so the final boundaries on x are:
\(-4 \leq x \leq 176\) (the minimum ones for which both inequalities stay true).
n = -2 gives x = 255n = -1 gives x = 135n = 0 gives x = 15n = 1 gives x = -105n < -2 gives x > 255, and n > 1 gives x < -105
So, values of n for which \(-4 \leq x \leq 176\) is true are n = -1, or n = 0
Thus, x = either 135 or 15
sin
Thus, the value of x which saisfies the equation sin(x+37)°=cos(2x+8)° is 135 or 15
Learn more about sine to cosine conversion here:
https://brainly.com/question/1421592
This is a really hard question- Help

Answers
Answer:
680
Step-by-step explanation:
x = total number
.6x = bus riders = 408 (.6 is decimal for 60%)
.6x = 408
x = 408/.6 = 680
Necesito ayuda urgenteee
Un cine tiene 800 butacas: durante la semana la asistencia fue: el lunes
2/5, martes 4/5, miércoles 4/5, jueves 1/5, viernes 3/5, sábado y domingo
completo. El precio de la entrada 8’7 €. ¿Cuál fue la recaudación de toda
la semana?
Answers
The total collection is 33408
What is unitary method?The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.
Given:
Total = 800 seats
On Monday 2/5
So, seats= 800*2/5 = 1600/5
=320 seats
On Tuesday
seats = 800 * 4/5
=3200/5
= 640
On Wednesday
seats = 800 * 4/5
=3200/5
= 640
On Thursday
seats = 800 * 1/5
=800/5
= 160
On Friday
seats = 800 * 3/5
=2400/5
= 480
As, the ticket price is €8.7
On Monday price of ticket = 320*8.7=2784On Tuesday price of ticket = 640*8.7=5568On Wednesday price of ticket = 640*8.7= 5568On Thursday price of ticket = 160*8.7=1392On Friday price of ticket = 480*8.7=4176On Saturday price of ticket = 800*8.7=6960On Sunday price of ticket = 800*8.7=6960Hence, the total collection = 33408
Learn more about unitary method here:
https://brainly.com/question/22056199
#SPJ1
The translation of the complete question is
I need urgent help
A cinema has 800 seats: during the week the attendance was: on Monday
2/5, Tuesday 4/5, Wednesday 4/5, Thursday 1/5, Friday 3/5, Saturday and Sunday complete. The ticket price is €8.7. What was the collection of all
week?
67% of teenagers, ages fifteen to seventeen, are concerned about their credit scores. Suppose we randomly select fifteen- to seventeen-year-old teenagers until we find one who is concerned about his/her credit score. Let X be the number of teenagers we select who are not concerned about their credit scores before we find the first teenager who is concerned . Let Y be the number of teenagers we select who are not concerned about their credit scores before the second teenager who is concerned is found.
a. What is the probability that none of the first three people are concerned about their credit scores?
b. What is the expected value of X?
c. What is the variance of X?
d. What is the probability that X = 0?
e. What is the probability that X ≤ 4?
f. What is the probability that Y = 6?
g. What is the probability that Y = 0?
Answers
The probability of the following parts is: a. 0.33 b. 1.925 c. 0.176 d. 0.67 e. 0.99955416 f. 0.018318006 g. 0.4489
a. To find out the probability that none of the first three people is concerned about their credit scores, we need to find: P(none of the first three is concerned about their credit scores)we have been given the probability that a teenager is concerned about his/her credit score is 0.67. So the probability that a teenager is not concerned about his/her credit score is 0.33. Now we can say that this is a binomial distribution since we are repeating a procedure until success is achieved. So we can use the binomial distribution to find the above probability: P(none of the first three are concerned about their credit scores) = (0.33)^3 = 0.0359375
b. The expected value of X is given by: E(X) = 1/p = 1/0.67 = 1.4925
c. Variance of X is given by: Var(X) = (1-p)/p^2 = (0.33)/(0.67)^2 = 0.176
d. Since X is the number of teenagers we select who are not concerned about their credit scores before we find the first teenager who is concerned. The probability that X = 0 is the probability that the first teenager we select is concerned about his/her credit score, which is given by: P(X = 0) = p = 0.67
e. To find out the probability that X ≤ 4, we can use the complement rule: P(X ≤ 4) = 1 - P(X > 4) = 1 - [P(X = 5) + P(X = 6) + ....... to ∞] = 1 - (1 - p)^5 = 1 - (0.33)^5 = 0.99955416
f. To find out the probability that Y = 6, we need to find: P(Y = 6)We know that for Y = 6, we need to select 7 teenagers such that the first and the second teenager we select are not concerned about their credit scores, and the third to the seventh teenager we select are concerned about their credit scores. The probability that the first and the second teenager we select are not concerned about their credit scores is given by: P(selecting 2 teenagers not concerned about their credit scores) = (0.33)^2 = 0.1089 And the probability that the third to the seventh teenager we select are concerned about their credit scores is:
P(selecting 5 teenagers concerned about their credit scores) = (0.67)^5 = 0.16806957Therefore, P(Y = 6) = P(selecting 2 teenagers not concerned about their credit scores) * P(selecting 5 teenagers concerned about their credit scores) = 0.018318006
g. To find out the probability that Y = 0, we need to select the first two teenagers who are concerned about their credit scores. P(Y = 0) = P(selecting the first two teenagers who are concerned about their credit scores) = (0.67)^2 = 0.4489.
To learn more about "Probability": brainly.com/question/30092244
#SPJ11
Manny has $12,000 and is saving for a used car that costs $15,000. He is able to save $300. 00 per month toward his car. Write and solve an inequality for this situation if m represents the number of months that Manny must save to buy the car.
Answers
Manny must save for at least 50 months to have enough money to buy the car. this can be solved by setting up an inequality expression for the condition.
Let's set up an inequality to represent Manny's saving situation.
Manny saves $300.00 per month, so the total amount he will save in m months is 300m. The cost of the used car is $15,000.
To buy the car, Manny needs to save enough money, which can be represented by the inequality: 300m ≥ 15000
This inequality states that the total amount Manny saves, 300m, must be greater than or equal to $15,000, the cost of the car. To solve this inequality for m, we can divide both sides of the inequality by 300: m ≥ 15000/300
Simplifying this expression, we get: m ≥ 50
Therefore, Manny must save for at least 50 months to have enough money to buy the car.
learn more about inequality here: brainly.com/question/20383699
#SPJ11
how to solve this story problem. Newton buys 4 gallons of gasoline. He pays $8.64. How much does 1 gallon of gasoline cost
Answers
Answer:
$2.16 / gallon
Step-by-step explanation:
4 gallons were bought for $8.64
4 gallons = $8.64
1 gallon = ?
cross multiply and divide
$8.64 / 4 gallons = $2.16 per gallon
check:
$2.16 * 4 = $8.64
You divide $8.64 by 4
what is the value of x (x+2)(x-3)=0
Answers
Answer:
x = 3 or x = -2
Step-by-step explanation:
Solve for x over the real numbers:
(x + 2) (x - 3) = 0
Hint: | Find the roots of each term in the product separately.
Split into two equations:
x - 3 = 0 or x + 2 = 0
Hint: | Look at the first equation: Solve for x.
Add 3 to both sides:
x = 3 or x + 2 = 0
Hint: | Look at the second equation: Solve for x.
Subtract 2 from both sides:
Answer: x = 3 or x = -2
The graph shows the relationship between the number
of cups of flour and the number of cups of sugar in
Angela's brownie recipe.
The table shows the same relationship for Jaleel's
brownie recipe.
Jaleel and Angela buy a 12-cup bag of sugar and divide
it evenly to make their recipes.
If they each use ALL of their sugar, how much FLOUR
do they each need?
Answers
Angela's use 6 cups of flour and Jaleel's use 19/3 cups of flour.
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The graph shows the relationship between the number of cups of flour and the number of cups of sugar in Angela's brownie recipe.
And, The table shows the same relationship for Jaleel's brownie recipe.
Hence, The equation for Angela's brownie recipe is,
Two points on graph are (4, 2) and (2, 1)
⇒ y - 2 = (2 - 1)/ (4 - 2) (x - 4)
⇒ y - 2 = 1/2 (x - 4)
⇒ y - 2 = 1/2x - 2
⇒ y = 1/2x
And, The equation for Jaleel's brownie recipe is,
Two points on graph are (3/2, 1) and (3, 2)
⇒ y - 1 = (2 - 1)/ (3 - 3/2) (x - 4)
⇒ y - 1 = 2/3 (x - 4)
⇒ y - 1 = 2/3x - 8/3
⇒ y = 2/3x - 8/3 + 1
⇒ y = 2/3x - 5/3
So, For Jaleel and Angela buy a 12-cup bag of sugar.
The equation for Angela's brownie recipe is,
⇒ y = 1/2x
⇒ y = 1/2 × 12
⇒ y = 6
The equation for Jaleel's brownie recipe is,
⇒ y = 2/3x - 5/3
⇒ y = 2/3 × 12 - 5/3
⇒ y = 19/3
Thus, Angela's use 6 cups of flour and Jaleel's use 19/3 cups of flour.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1

explain how overflow makes two’s complement numbers act negative.
Answers
overflow in two's complement arithmetic causes the wrap-around of the most significant bit, resulting in the representation of positive numbers as negative numbers.
In two's complement representation, numbers are represented using a fixed number of bits. The most significant bit (MSB) is reserved to indicate the sign of the number, where 0 represents a positive number and 1 represents a negative number.
Overflow occurs in two's complement arithmetic when the result of an operation exceeds the range that can be represented with the available number of bits.
When overflow occurs, the result is truncated or wrapped around to fit within the bit representation. This wrapping around effectively causes the MSB to flip its value, changing the sign of the number. As a result, the number that was intended to be positive becomes negative in the two's complement representation.
For example, consider an 8-bit two's complement representation. The range for a signed 8-bit number is -128 to +127. If we add 1 to the maximum positive value of 127, overflow occurs because the result exceeds the range. The binary representation of 127 is 01111111, and adding 1 results in 10000000. Since the MSB changed from 0 to 1, the number is interpreted as -128 in two's complement representation.
In summary, overflow in two's complement arithmetic causes the wrap-around of the most significant bit, resulting in the representation of positive numbers as negative numbers.
To know more about two's complement arithmetic refer here:
https://brainly.com/question/15125604
#SPJ11
does the confidence interval suggest that the difference, if any, observed in this sample will also generalize to the larger population?
Answers
In the following question, Yes, the confidence interval suggests that the difference observed in this sample will also generalize to the larger population.
What is a confidence interval? A confidence interval is a probability statement that provides an interval of plausible values that are likely to contain the value of a population parameter. It is a way to infer the population parameter value from sample data.
A confidence interval is calculated as a range of values that are predicted to include the unknown population parameter, based on the sample statistic. The confidence interval suggests that the difference, if any, observed in this sample will also generalize to the larger population.
A confidence interval with a high level of confidence (e.g. 95%) would have a wider range of values and a higher probability of including the population parameter. The interpretation of the confidence interval is that we are 95% confident that the actual population parameter falls within the calculated interval. Therefore, it implies that the sample data is likely to be representative of the population data.
For more such questions on confidence interval
https://brainly.com/question/17097944
#SPJ11
I just need an answer to this. I’ve tried everything I’ve erased so much, my paper is starting to wear out.

Answers
Answer:
2x²- 10x + 8
3x² - x - 4
Step-by-step explanation:
Answer:
hope this helps..........
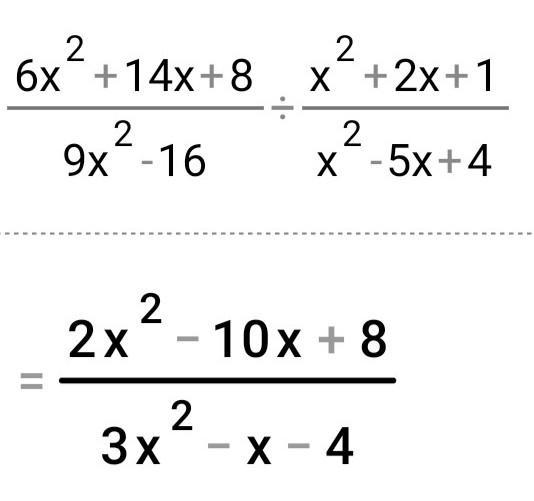
plz help am just dumb today...

Answers
Answer:
C and D!
Step-by-step explanation:
For A, two is greater than negative four, so that eliminates that right off the bat.
In B, -1/3 is greater than -1/6, so that choice is wrong.
E, -3/4 is greater than negative three, so that is also wrong!
C and D are correct!
If you need extra help, I'm here!
Answer:
B,D
Step-by-step explanation:
They are ordered correctly
Brainliest appreciated!
Please solve for the following.
Don’t be a child, real answers only :)

Answers
George walks 1 mile to school. He leaves home at the same time each day, walks at a steady speed of 3 miles per hour, and arrives just as school begins. Today he was distracted by the pleasant weather and walked the first 1/2 mile at a speed of only 2 miles per hour. At how many miles per hour must George run the last 1/2 mile in order to arrive just as school begins today?
Answers
Answer:
George must run the last half mile at a speed of 6 miles per hour in order to arrive at school just as school begins today
Step-by-step explanation:
Here, we are interested in calculating the number of hours George must walk to arrive at school the normal time he arrives given that his speed is different from what it used to be.
Let’s first start at looking at how many hours he take per day on a normal day, all things being equal.
Mathematically;
time = distance/speed
He walks 1 mile at 3 miles per hour.
Thus, the total amount of time he spend each normal day would be;
time = 1/3 hour or 20 minutes
Now, let’s look at his split journey today. What we know is that by adding the times taken for each side of the journey, he would arrive at the school the normal time he arrives given that he left home at the time he used to.
Let the unknown speed be x miles/hour
Mathematically;
We shall be using the formula for time by dividing the distance by the speed
1/3 = 1/2/(2) + 1/2/x
1/3 = 1/4 + 1/2x
1/2x = 1/3 - 1/4
1/2x = (4-3)/12
1/2x = 1/12
2x = 12
x = 12/2
x = 6 miles per hour
Eli needs to order some new supplies for the restaurant where he works. The restaurant needs at least 546 knives. There are currently 312 knives. If each set on sale contains 10 knives, write and solve an inequality which can be used to determine xx, the number of sets of knives Eli could buy for the restaurant to have enough knives.
Answers
Answer:
The restaurant needs 546 knives and there is 312 knives
The amount remaining is 546-312=234
if each set contains 10 knives
The amount of set remaining is 234/10=23.4 sets