Answers
Applying the subtraction property of equality, the number that belongs in the green box is of 9.
What is the subtraction property of equality?When we subtract an amount from one side of the equality, the same amount has to be subtracted from the other side of the equality.
In this problem, we have that;
9 is subtracted from the left side of the equality, given by 2p + 9.Hence, 9 also has to be subtracted from the right side of the equality, given by 27.Thus, the number that belongs in the green box is of 9.
More can be learned about the subtraction property of equality at https://brainly.com/question/1601404
#SPJ1
Related Questions
I need some help over here

Answers
The measure of angle ∠WDY is 89° in problem 20.
What is angle?Two rays (half-lines) that share an endpoint make up an angle. The rays serve as the angle's sides, occasionally serving as the angle's legs and occasionally serving as its arms, while the latter is referred to as the vertex of the angle.
Two angles are said to be congruent by this definition if either of their vertex and side coordinates can be rigidly moved to coincide with the other. The angle may be written as AOB or BOA if O is the vertex and A and B are the points on the two sides (and this for any selection of the two points A and B.)
Given that D is the common point of line segments DW, DX and DY
m∠WDX = 2x - 5
m∠XDY = 52
m∠WDY = 5x - 16
to find m∠WDY
m∠WDY = m∠XDY + m∠WDX
5x - 16 = 52 + 2x - 5
5x - 2x = 52 - 5 + 16
3x = 63
x = 63/3
x = 21
m∠WDY = 5(21) - 16
m∠WDY = 89
Thus, the measure of angle ∠WDY is 89° in problem 20.
Learn more about angles
https://brainly.com/question/28451077
#SPJ1
one of the features of the interactive model of communication that is discussed in chapter one by turner and west which makes it different from the linear model that was based on shannon and weaver's mathematical model of communication is:
Answers
One of the features of interactive model of communication is "Feedback where a recipient of communication such as a listener provides a response to a message, often to indicate understanding after a message has been received."
The Feedback is one of the key features that makes the Interactive Model of Communication different from the Linear Model based on Shannon and Weaver's mathematical model .
The Feedback allow a reciprocal exchange of messages between the sender and receiver, making communication a dynamic and interactive process.
In the Interactive Model, the feedback enables the receiver to provide feedback to the sender, which allows clarification, confirmation, and correction of messages.
The given question is incomplete , the complete question is
One of the features of the interactive model of communication that is discussed by Turner and West which makes it different from the linear model that was based on Shannon and weaver's mathematical model of communication is ?
Learn more about Shannon and Weaver Model here
https://brainly.com/question/18272831
#SPJ4
You start at 1,-4 you move right 2 units where do you end
Answers
Answer:
(3,-4)
Step-by-step explanation:
+2 only to x if moving left to right
Answer: You would end up at 1 -2.
Step-by-step explanation: I've been doing this for about 2 weeks and I worked it out on a paper.
Write the equation of the line fully simplified slope-intercept form.

Answers
Answer:
Using the points (0,8)(2,5)(4,2)(6,-1)
Step-by-step explanation:
y=mx+b form/ slope intercept is -3/2x+8
solpe is -3/2
Y-intercept is (0,8)
1. What is the solution set for this inequality?
-14x + 12 < -100
A. x < 8
B. x >8
C. X>6
D. x< 14
please help
Answers
4(2x + 3) ÷ 5y
From the expression above, provide an example of each of the following: sum, term, product, factor, quotient, and coefficient. If any are not present, write "not present."
Answers
Answer:
Sum: Not present.
Product: 12 (achieved by using the distributive property to multiply 4 by 3).
Term: x
Factor: Not present (I think.)
Quotient: Not present.
Coefficient 2 (placed before x).
Step-by-step explanation:
Use the distributive property & multiply the 2x + 3 inside the parenthesis using the 4 outside the parenthesis.Then, multiply the y to both sides, to get \(\frac{(8x+12) * y}{5}\).Distribute by multiplying y with 8x + 12 using the distributive property.Your final result will be: \(\frac{8xy + 12y}{5}\).
From the expression, we get
Sum: Not present.Product: 12 (achieved by using the distributive property to multiply 4 by 3).Term: xFactor: Not present (I think.)Quotient: Not present.Coefficient 2 (placed before x).What is an expression?An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division. The terms involved in an expression in math are: Constant: A constant is a fixed numerical value. Variable: A variable is a symbol that doesn't have a fixed value.
What is distributive property short answer?The distributive property is a property of multiplication used in addition and subtraction. This property states that two or more terms in addition or subtraction with a number are equal to the addition or subtraction of the product of each of the terms with that number.
Learn more about the distributive property here: brainly.com/question/27445861
#SPJ2
A study was performed with a random sample of 200 people from one college. What population would be appropriate for generalizing conclusions from the study, assuming the data collection methods used did not introduce biases? Select the correct answer below:
A. The conclusions should apply to all people in the same country.
B. The conclusions should apply to all people within the same city as the college.
C. The conclusions should apply to people at that particular college.
D. The conclusions should apply to people at any college.
E. The conclusions apply only to the sample.
Answers
Based on the information provided, the appropriate population for generalizing conclusions from the study would be C. The conclusions should apply to people at that particular college.
Since the study was conducted using a random sample of 200 people from one college, the conclusions drawn from the study are most likely applicable to the population of people at that specific college. It would be incorrect to assume that the conclusions can be generalized to all people in the same country (Option A), all people within the same city as the college (Option B), people at any college (Option D), or that the conclusions apply only to the sample (Option E).
To know more about generalizing visit-
brainly.com/question/26855809
#SPJ11
in 250 explain the power of substitutes from porters 5
forces
Answers
The power of substitutes is one of the five forces in Porter's Five Forces framework and it is a measure of how easy it is for customers to switch to alternative products or services. The higher the power of substitutes, the more competitive the industry and the lower the profitability.
The power of substitutes is based on the premise that when there are readily available alternatives to a product or service, customers can easily switch to those alternatives if they offer better value or meet their needs more effectively. This poses a threat to the industry as it reduces customer loyalty and puts pressure on pricing and differentiation strategies.
The availability and quality of substitutes influence the degree to which customers are likely to switch. If substitutes are abundant and offer comparable or superior features, the power of substitutes is strong, increasing the competitive intensity within the industry. On the other hand, if substitutes are limited or inferior, the power of substitutes is weak, providing more stability and protection to the industry.
To know more about Porter's Five Forces framework here: brainly.com/question/32990982
#SPJ11
PLEASE HELP ASAP 20 PTS
1. Name two vertical angles.
2. Name a linear pair with vertex B.
3. Name an angle not adjacent to, but complementary to ZFGC.
4. Name an angle adjacent and supplementary to ZDCB.
5. Write the statement All dogs have four feet in if-then form.

Answers
Find the vertex of the quadratic polynomial, f(x) = 4x² -8x + 6
Answers
The equation of a parabola with vertex (h,k) is given by:
\(y=a(x-h)^2+k\)Starting from the given equation, complete the square to write the function in vertex form:
\(\begin{gathered} f(x)=4x^2-8x+6 \\ =4(x^2-2x)+6 \\ =4(x^2-2x+1-1)+6 \\ =4(x^2-2x+1)+4(-1)+6 \\ =4(x-1)^2-4+6 \\ =4(x-1)^2+2 \end{gathered}\)By comparing that equation with the vertex form of a parabola, we can see that h=1 and k=2.
Therefore, the vertex of the given quadratic polynomial, is:
\((1,2)\)Answer:
I think its -128x + 6
Step-by-step explanation:
Consider the differential equation dy/dx=xy^4.
Find ⅆ2yⅆx2 in terms of x and y. Determine the concavity of all solution curves for the given differential equation in Quadrant II. Give a reason for your answer.
Answers
Answer:
To find the second derivative of y with respect to x, we can take the derivative of the given differential equation with respect to x:
dy/dx = xy^4 d/dx(dy/dx) = d/dx(xy^4) d2y/dx2 = y^4 + 4xy^3(dy/dx)
Substituting the given differential equation into the expression for the second derivative, we get:
d2y/dx2 = y^4 + 4xy3(xy4) = y^4 + 4x2y7
In Quadrant II, x is negative and y is positive. Since y^4 and y^7 are both positive for any value of y, the expression for the second derivative simplifies to:
d2y/dx2 = y^4(1 + 4x2y3)
Since x is negative in Quadrant II, the quantity (1 + 4x2y3) is positive. Therefore, d2y/dx2 is positive for all values of x and y in Quadrant II. This means that all solution curves for the given differential equation are concave up in Quadrant II.
Received message. To find the second derivative of y with respect to x, we can take the derivative of the given differential equation with respect to x: dy/dx = xy^4 d/dx(dy/dx) = d/dx(xy^4) d2y/dx2 = y^4 + 4xy^3(dy/dx) Substituting the given differential equation into the expression for the second derivative, we get: d2y/dx2 = y^4 + 4xy^3(xy^4) = y^4 + 4x^2y^7 In Quadrant II, x is negative and y is positive. Since y^4 and y^7 are both positive for any value of y, the expression for the second derivative simplifies to: d2y/dx2 = y^4(1 + 4x^2y^3) Since x is negative in Quadrant II, the quantity (1 + 4x^2y^3) is positive. Therefore, d2y/dx2 is positive for all values of x and y in Quadrant II. This means that all solution curves for the given differential equation are concave up in Quadrant II.
Step-by-step explanation:
The scatter plot shows the number of households, in millions, that have cable television over eight consecutive years. Which of the following is an appropriate line of best fit?
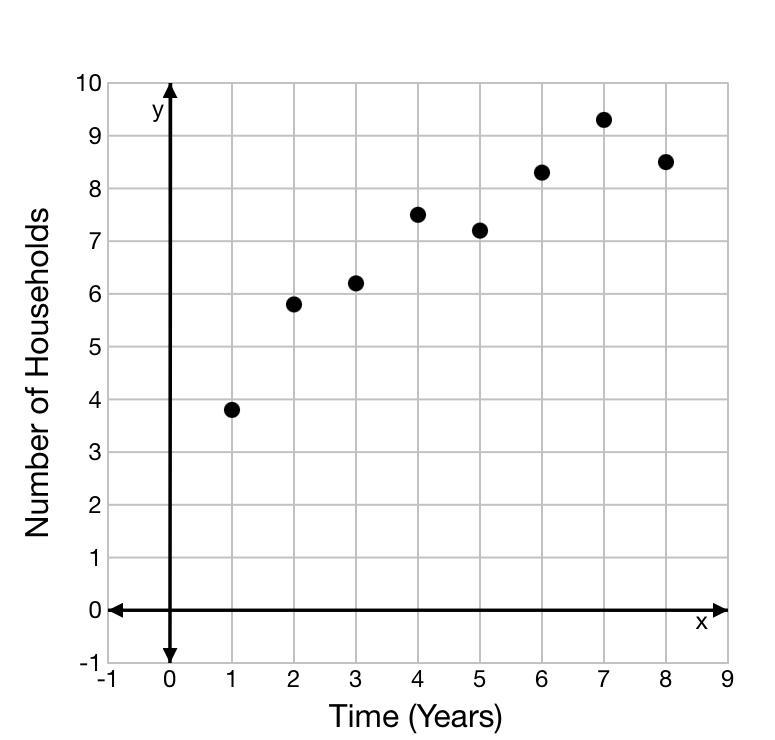
Answers
The equation of the appropriate line of best fit is y = 1.25x + 2
How to determine the line of best fit?Start by drawing a line through the points (see attachment)
From the attached graph, we have:
(x, y) = (0,2) and (4,6.5)
Calculate the slope (m) using:
m = (y2 - y1)/(x2 - x1)
This gives
m = (6.5 - 4)/(2 - 0)
Evaluate
m = 1.25
The equation is then calculated as:
y = m(x - x1) + y1
This gives
y = 1.25(x - 0) + 2
Expand
y = 1.25x + 2
Hence, the equation of the appropriate line of best fit is y = 1.25x + 2
Read more about line of best fit at:
https://brainly.com/question/1518824
#SPJ1

Darin receives a $3,000 commission for the first 10 cars he sells and 450 for each additional car he sells. Which of the following expresses the commission C, in dollars, Darin receives if he sells x cars in a month, where x > 10 ?
A. C= 450x + 3, 000
B. C= 450x-1,500
C. C = 350x - 1, 50c
D. C = 450x + 1, 500
Answers
Answer:
A C= 450x + 3,000
Step-by-step explanation:
if Darin sells more than 10 cars, you have to multiplicate 450 * x (number bigger than 10) plus 3000
4.solve for x and y
pls help

Answers
Answer:
x = 4\(\sqrt{3}\)
y = 8\(\sqrt{3}\)
Step-by-step explanation:
this is a 30-60-90 triangle and the sides have a constant ratio
the side across from the 30°∡ is 1
the side across from the 60°∡ is √3
the side across from the 90°∡ is 2
In this problem we can find 'x' by setting up this proportion:
x/12 = \(\sqrt{3}\)/1
cross-multiply:
\(\sqrt{3}\)x = 12
x = 12/\(\sqrt{3}\)
since we don't like to leave radicals in the denominator, we can multiply both numerator and denominator by \(\sqrt{3}\) to get:
12\(\sqrt{3}\) ÷ \(\sqrt{3}\)·\(\sqrt{3}\) (\(\sqrt{3}\)·\(\sqrt{3}\) = \(\sqrt{9}\), which equals 3)
so we have 12\(\sqrt{3}\)/3, which is 4\(\sqrt{3}\)
The 'y' value will be twice the 30° side, so 8\(\sqrt{3}\)
A cone-shaped paper drinking cup is to be made to hold 36 cm3 of water. Find the height and radius of the cup (in cm) that will use the smallest amount of paper. (Round your answers to two decimal places.) height cm radius cm
Answers
The height and radius of the cup are 4.41 cm and 2.07 cm respectively
To minimize the amount of paper used, we need to minimize the surface area of the cup. Let h be the height and r be the radius of the cone. Then we have:
\(Volume of cone = \frac{1}{3} πr^{2} h = 36 cm^{3}\)
Solving for h, we get:
\(h = \frac{108}{(πr^2)}\)
Now we can express the surface area of the cone as:
\(Surface area = πr^2+ πr\sqrt{r^{2}+h^{2} }\)
Substituting the expression for h, we get:
\(Surface area = πr^2+πr \sqrt{(r^{2} +(\frac{108}{(πr^2)^{2}) } )}\)
To minimize this function, we take its derivative with respect to r and set it equal to zero:
\(\frac{d}{dx} (Surface area) = \frac{2πr - 108r }{[(r^2+(\frac{108}{πr^2}))^{0.5} }] - \frac{108π}{r^2 } = 0\)
Simplifying, we get:
\(2r^3 - \frac{108^2}{π} = 0\)
Solving for r, we get:
\(r = (\frac{54}{π})^{\frac{1}{3} }\)
Substituting this value into the expression for h, we get:
\(h = \frac{108}{\frac{54}{π} ^{(\frac{2}{3}π )} }\)
Thus, the height and radius of the cup that will use the smallest amount of paper are:
height = 4.41 cm
radius = 2.07 cm (rounded to two decimal places)
To know more about "Volume of cone" refer here:
https://brainly.com/question/1984638#
#SPJ11
For part of a recipe, Jada adds 0. 35 milliliters of vanilla extract to 16. 4 milliliters of milk. How many milliliters does the mixture contain?
Answers
Answer: The answer to this question is 16.75.
Step-by-step explanation:
16.40
+ 0.35
16.75
Evaluate (−23)×(−23)3 by using the Laws of Exponents
Answers
Given:
\(\left(-\dfrac{2}{3}\right)\times \left(-\dfrac{2}{3}\right)^3\)
To find:
The value of given expression by using the Laws of Exponents.
Solution:
We have,
\(\left(-\dfrac{2}{3}\right)\times \left(-\dfrac{2}{3}\right)^3\)
Using the Laws of Exponents, we get
\(=\left(-\dfrac{2}{3}\right)^{1+3}\) \([\because a^ma^n=a^{m+n}]\)
\(=\left(\dfrac{-2}{3}\right)^{4}\)
\(=\dfrac{(-2)^4}{(3)^4}\) \([\because \left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}]\)
\(=\dfrac{(-2)\times (-2)\times (-2)\times (-2)}{(3)\times (3)\times (3)\times (3)}\)
\(=\dfrac{16}{81}\)
Therefore, the value of given expression is \(\dfrac{16}{81}\).
A plane can fly 640 miles in the same time as it takes a car to go 240 miles. If the car travels 100 mph slower than the plane, find the speed (in mph) of the plane.
Answers
Answer:
Let s be the speed of the plane. Then s - 100 is the speed of the car.
640/s = 240/(s - 100)
640(s - 100) = 240s
8(s - 100) = 3s
8s - 800 = 3s
5s = 800, so s = 160 mph
The speed of the plane is 160 mph, and the speed of the car is 60 mph.
what expression is the sane as 1/2 x 5

Answers
Answer:
5 divided by 2
Step-by-step explanation:
1/2 * 5 = 5/2
5/2 = 5 divided by 2
A bird flying at an elevation of 110 ft swoops down to grab a mouse on top of a 3 foot tall rock. What is the change in the birds elevation?
Answers
Answer:
Bird swoops down by 107 feet to grab a mouse on top of a \(3\) foot tall rock
Step-by-step explanation:
Given
The level of mouse from the ground is \(3\) foot as it is on the top of a \(3\) foot tall rock.
The level of bird at which it is flying from the ground is \(110\) feet
Change in elevation when the bird swoops down to grab the mouse
\(= 110 -3\\= 107\)feet
Bird swoops down by 107 feet to grab a mouse on top of a \(3\) foot tall rock
Problem: Construct a triangle with interior angle measures of 60° and 60°. Let one of the side lengths be 10. What are the lengths of the other sides?
Answers
Answer:
Step-by-step explanation:
Given a triangle with angles 60° and 60°. Let the third angle be represented by x, so that;
x + 60° + 60° = \(180^{o}\) (sum of angle in a triangle)
x + 120 = \(180^{o}\)
x = \(180^{o}\) - 120
x = 60°
Thus, since the third angle of the triangle is 60°, then the triangle is an equilateral triangle. For an equilateral triangle, all sides are equal and all its angles are equal. So that the other sides of the triangle is 10 each.
<ABC ≅ <BAC ≅ < ACB ≅ 60°
AB = BC = AC = 10 cm
The required construction for the question is attached to this answer for more clarifications.

Answer:
It's an obtuse angle
Step-by-step explanation:
Tommy mows lawns in the summer for extra cash. He charges a flat $5 fee and then $6.50 per hour. Let h represent the number of hours Tommy has worked. Expression: If Tommy works 4 hours on Saturday, find out how much he made?
Answers
Answer:
$31
Step-by-step explanation:
You have to do 6.5*4 first since 4 is the number of hours. With that, you will get 26. After that, you need to add a 5 since 5 is the flat fee. At the end, you will get $31.
PLEASEEEEEEEEEEEEEEEEEEEEEEE HELP ME!!!!

Answers
Michael invest $600 in an account with a 3% interest simple interest rate. The account is open for 10 years. How much interest did he earn after 10 years?
A: $150
B: 180
C: 18000
D: 1800
Answers
Answer:
$180
Step-by-step explanation:
Interest = Principal * rate * time
= 600 * .03 * 10
= 180
Principal + Interest = Total value
$600 + $180 = $780
a four digit personal identification number (pin) is selected. what is the probability that there are no repeated digits? do not round
Answers
If a four digit personal identification number is selected, then the probability that there are no repeated digits is 0.504
Number of digits in the identification number = 4
0, 1, 2, 3, 4, 5, 6, 7, 8 and 9
There are 10 digits
The probability = Number of favorable outcomes / Total number of outcomes
Total number of outcomes = 10 × 10 × 10 × 10
= 10000
Number of outcomes that digits wont repeat = 10 × 9 × 8 × 7
= 5040
Substitute the values in the equation of probability
The probability = 5040 / 10000
= 0.504
Therefore, the probability there are no repeated digits is 0.504
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Ben Collins plans to buy a house for \( \$ 184,000 \). If the reol estate in his area is expected to increase in value 3 percent each year, what will its approximate value be six years from now? Use E
Answers
Ben Collins plans to buy a house for $184,000, and if the real estate in his area is expected to increase in value by 3 percent each year, its approximate value will be around $208,943.95 six years from now.
To calculate the approximate value of the house six years from now, we can use the formula for compound interest: \(\(A = P(1 + r/n)^{nt}\), where \(A\)\) is the future value, \(\(P\\)) is the principal amount, \(\(r\)\) is the annual interest rate (expressed as a decimal), \(\(n\)\) is the number of times that interest is compounded per year, and \(\(t\)\) is the number of years.
In this case, the principal amount is $184,000, the annual interest rate is 3 percent (or 0.03 as a decimal), the compounding is done annually \((so \(n = 1\))\), and the time period is 6 years. Plugging these values into the formula, we get:
\(\(A = 184,000(1 + 0.03/1)^{(1)(6)}\)\)
Simplifying the equation, we have:
\(\(A = 184,000(1.03)^6\)\)
Evaluating this expression, we find:
\(\(A \approx 208,943.95\)\)
Therefore, the approximate value of the house six years from now would be around $208,943.95, assuming a 3 percent annual increase in real estate value.
Learn more about percent here:
https://brainly.com/question/16797504
#SPJ11
Maximize Z = 120 x1 + 80 x2, S.T. x1 ≤ 40 x2 ≤ 10 20 x1 + 10 x2 < 500 and x1 ≥ 0, x2 ≥ 0. Use the graphical method to solve this model (show detailed work)
Answers
the optimal solution to maximize Z is x1 = 25 and x2 = 0, with Z = 3000.
To solve the given linear programming model graphically, we need to plot the feasible region and identify the corner points to find the optimal solution. Here's the step-by-step process:
1. Plot the constraints:
- Plot the line x1 = 40 (vertical line at x1 = 40).
- Plot the line x2 = 10 (horizontal line at x2 = 10).
- Plot the line 20x1 + 10x2 = 500 (which can be rewritten as 2x1 + x2 = 50).
- Shade the feasible region that satisfies all the constraints.
2. Identify the corner points:
- Determine the coordinates of the corner points where the boundary lines intersect.
3. Evaluate the objective function:
- Calculate the value of the objective function Z = 120x1 + 80x2 for each corner point.
4. Determine the optimal solution:
- Select the corner point that maximizes the objective function Z.
Here's the graphical representation of the feasible region:
|
40 | C
| /
| /
| /
| /
| /
| / Feasible Region
10 |_____/_________________
0 10 20 30 40 50
0`
The corner points of the feasible region are:
A: (0, 0)
B: (0, 10)
C: (25, 0)
D: (20, 5)
Now, we evaluate the objective function Z = 120x1 + 80x2 for each corner point:
Z(A) = 120(0) + 80(0) = 0
Z(B) = 120(0) + 80(10) = 800
Z(C) = 120(25) + 80(0) = 3000
Z(D) = 120(20) + 80(5) = 2400
From the above calculations, we can see that the maximum value of Z occurs at point C: (25, 0).
To know more about function visit:
brainly.com/question/30721594
#SPJ11
hii please help i’ll give brainliest:)

Answers
Answer: Caravans
Step-by-step explanation:
Please help me with number 10

Answers
Hope it helped
work out the value of T using the formula T=3x^{2]p-2p when p= -1?
Answers
The solution of the equation when p = -1 is \(T=3x^{-2}\)
How to determine the value of the equation?The equation is given as:
\(T=3x^{2p}\)
The value of p is -1.
So, we have:
\(T=3x^{2*-1}\)
Evaluate the product
\(T=3x^{-2}\)
Hence, the solution of the equation when p = -1 is \(T=3x^{-2}\)
Read more about equations at:
https://brainly.com/question/18797214
#SPJ1
