factorise 3(x-y)^2 - 2(x-y)
Answers
Answer:
\((x - y) [3(x - y) - 2]\)
Step-by-step explanation:
\(3(x - y)^{2} - 2(x - y)\)
Lets take \((x - y)\) common from the expression.
\(=> (x - y) [3(x - y) - 2]\)
The factors of the expression 3(x - y)² - 2(x - y) will be (3x - 3y - 2) and (x - y).
What is factorization?It is a method for dividing a polynomial into pieces that will be multiplied together. At this moment, the polynomial's value will be zero.
The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.
The expression is given below.
⇒ 3(x - y)² - 2(x - y)
Simplify the expression, then we have
⇒ 3(x - y)² - 2(x - y)
⇒ (x - y)[3(x - y) - 2]
⇒ (x - y)(3x - 3y - 2)
The factors of the expression 3(x - y)² - 2(x - y) will be (3x - 3y - 2) and (x - y).
More about the factorization link is given below.
https://brainly.com/question/6810544
#SPJ2
Related Questions
Given a collection of 2023 closed squares of total area 4, prove that they can be arranged to cover a unit square (overlaps are allowed)
Answers
We can arrange the 2023 squares to cover the unit square, with overlaps allowed.
We can prove that a collection of 2023 closed squares of total area 4 can be arranged to cover a unit square by using the pigeonhole principle. Since the total area of the squares is 4, the average area of each square is 4/2023. Let's take a unit square and divide it into 2023 smaller squares of area (1/2023) each. By the pigeonhole principle, we can assign one of the 2023 squares to each of the smaller squares. Since the average area of each square is 4/2023, each of the assigned squares will overlap with at most 4 other squares. Therefore, we can arrange the 2023 squares to cover the unit square, with overlaps allowed.
Learn more about the pigeonhole principle here: brainly.com/question/30322724
#SPJ4
at the newest animated movie, for every 9999 children, there are 4444 adults. there are a total of 39393939 children and adults at the movie.
Answers
In this movie, the ratio of children to adults suggests that there are 27 children in attendance.
We have to give that,
There are 9 children for every 4 adults.
This means that if there were 13 people, 9 of them would be children and 4 would be adults.
Children would therefore be:
= 9 / 13
If there were 39 people, the number of children would be:
= 9/13 x 39
= 27 children
In conclusion, there are 27 children.
To learn more about the function visit:
https://brainly.com/question/11624077
#SPJ4
The complete question is,
In the newest animated movie, for every 9 children, there are 4 adults. There are a total of 39 children and adults in the movie.
How many children are in the movie?
Pure copper was mixed with a 10% copper alloy to produce an alloy thát was 25% copper. How much of the pure copper and how much 10% alloy were used to produce 36 kg of 25% alloy?
Answers
Answer:
6kg pure copper and 30 kg 10% copper was mixed to give 36kg of 25% alloy
Step-by-step explanation:
Here, we want to produce 36 kg of 25% alloy
Let the Pure copper be x kg while 10% alloy be y kg
Pure copper is simply 100% copper
Thus;
x + y = 36 •••••(i)
Then;
100% of x + 10% of y = 25% of 36
= x + 0.1y = 9 •••••• ii)
From i x = 36-y
from ii, x = 9-0.1y
Equate both x
36-y = 9-0.1y
36-9 = 0.1y + y
0.9y = 27
y = 27/0.9
y = 30
x = 36-y
x = 36-30
x = 6 kg
Find the property for
9 • (-1 • x) = 9 • (-x)
Answers
Triangle ABC has the coordinates A(8,4) B(12,4) C(16,12) if the triangle is dilated with a scale factor of 1/4 what are the new coordinates
Answers
After dilating Triangle ABC with a scale factor of 1/4, the new coordinates of A', B', and C' are A'(2,1), B'(3,1), and C'(4,3), respectively.
To dilate Triangle ABC with a scale factor of 1/4, we need to multiply the coordinates of each vertex by the scale factor.
Let's apply the scale factor to each coordinate:
A' = (8 * 1/4, 4 * 1/4)
= (2, 1)
B' = (12 * 1/4, 4 * 1/4)
= (3, 1)
C' = (16 * 1/4, 12 * 1/4)
= (4, 3)
Therefore, after dilating Triangle ABC with a scale factor of 1/4, the new coordinates of A', B', and C' are (2,1), (3,1), and (4,3) respectively. The scale factor of 1/4 shrinks the original triangle by a factor of 1/4 in both the x and y directions, resulting in a smaller triangle with the new coordinates.
To learn more about scale factor click here: rainly.com/question/22312172
#SPJ11
Brainliest goes to whoever answers correctly and explains also if you want extra points answer my other questions
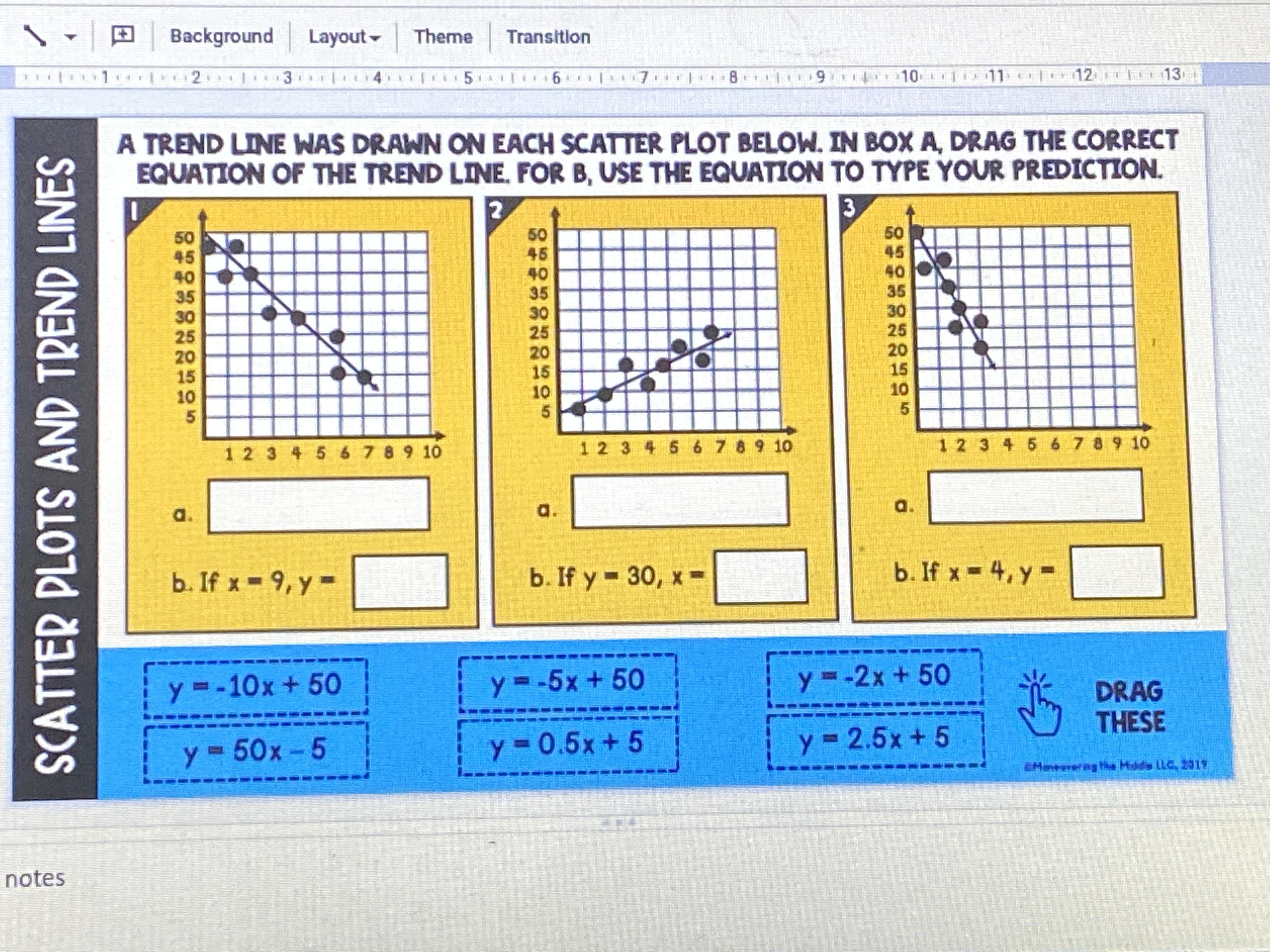
Answers
Answer:
1) y=-10x+50 (it's the only negative slope / going down option and it starts at x=0 y=50)
just substitute the x with a 9
y=-10*9 +50
y= -40
2) 0.5x +5 (only positive slop and starting point at x=0 is correctly 5)
we do need to substitute y this time, with 30 obviously
30 = 0.5x +5 |-5
25 = 0.5x | *2
50 = x
3) y=-2x +50 reasoning as before
substitute x with 4
y =-2*4 +50
y = -8 +50
y = 42
What is the amount if $960 is borrowed for 3 years at 10% interest?
Answers
Answer:
1248
Step-by-step explanation:
We know that
P = 960
T = 3 years
R = 10%
F = 960 + 960×10/100×3
960 + 96×3
960 + 288 = 1248

38. Data berat badan sekelompok anak adalah: 9, 17, 8, 12, 15, 15, 13, 10, 12, 10.
Median data tersebut adalah
Answers
Answer:
12
Step-by-step explanation:
Median data dihitung sebagai
= 1/2 (n + 1) suku ke-1
Dimana n = Jumlah suku
= 10
Langkah 1
Kami mengatur ulang
8, 9, 10, 10, 12, 12, 13, 15, 15, 17
Langkah 2
Suku 1/2 (n + 1)
1/2 (10 + 1) istilah
= 11/2 istilah
= 5,5 suku
Istilah ini antara istilah ke-5 dan ke-6
Suku ke-5 = 12
Suku ke-6 = 12
= 12 + 12/2 = 24/2
= 12
Median data adalah 12
Find a sinusoidal function with the following four attributes: (1) amplitude is 10, (2) period is 5, (3) midline is y = 31, and (4) ƒ(3) = 41. f(x) = =
Answers
The sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
To find a sinusoidal function with the given attributes, we can use the general form of a sinusoidal function:
f(x) = A * sin(Bx + C) + D
where A represents the amplitude, B represents the frequency (related to the period), C represents the phase shift, and D represents the vertical shift.
Amplitude: The given amplitude is 10. So, A = 10.
Period: The given period is 5. The formula for period is P = 2π/B, where P is the period and B is the coefficient of x in the argument of sin. By rearranging the equation, we have B = 2π/P = 2π/5.
Midline: The given midline is y = 31, which represents the vertical shift. So, D = 31.
f(3) = 41: We are given that the function evaluated at x = 3 is 41. Substituting these values into the general form, we have:
41 = 10 * sin(2π/5 * 3 + C) + 31
10 * sin(2π/5 * 3 + C) = 41 - 31
10 * sin(2π/5 * 3 + C) = 10
sin(2π/5 * 3 + C) = 1
To solve for C, we need to find the angle whose sine value is 1. This angle is π/2. So, 2π/5 * 3 + C = π/2.
2π/5 * 3 = π/2 - C
6π/5 = π/2 - C
C = π/2 - 6π/5
Now we have all the values to construct the sinusoidal function:
f(x) = 10 * sin(2π/5 * x + (π/2 - 6π/5)) + 31
Simplifying further:
f(x) = 10 * sin(2π/5 * x - 2π/10) + 31
f(x) = 10 * sin(2π/5 * x - π/5) + 31
Therefore, the sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
Learn more about sinusoidal function here
https://brainly.com/question/29529184
#SPJ11
5. The Survey of Study Habits and Attitudes (SSHA) is a psychological test, administered to students, that measures attitude towards school. Scores range from 0 to 200. The mean score for U.S. college students is about 117, and the standard deviation is about 23. A teacher who suspects that older students have better attitudes toward school gives SSHA to 40 students who are at least 30 years of age. Their mean score is x¯ = 133.8.
(a) Assuming that σ = 23 for the population of older students, carry out a test of H0 : µ = 117 Ha : µ > 117 Give the Z test statistic and its P-value.
(b) What do you conclude about older students’ attitudes toward school?
(c) Your test in the previous parts requires assumptions in addition to the assumption that the value of σ is known. What are they?
Answers
The Z-test statistic is 2.61 and the P-value is 0.0046. Based on the results, it can be inferred that older students exhibit more positive attitudes towards school compared to the average U.S. college student. To conduct the test, certain assumptions are necessary in addition to assuming the known value of σ: the sample is randomly selected from the population, and the population follows a normal distribution.
(a) The null hypothesis is H0: µ = 117 and the alternative hypothesis is Ha: µ > 117, and we will test the null hypothesis using the Z test statistic.
The test statistic Z is calculated as:
Z = (x¯ - µ) / (σ / sqrt(n))
where x¯ is the sample mean, µ is the population mean, σ is the population standard deviation, and n is the sample size.
Substituting the values we get, Z = (133.8 - 117) / (23 / sqrt(40))Z = 2.61The P-value corresponding to Z = 2.61 is 0.0046 using a Z table.
(b) The P-value of the test is 0.0046, which is less than the significance level of 0.05. Therefore, we can reject the null hypothesis and conclude that older students have better attitudes toward school than the average U.S. college student.
(c) The assumptions required for the test in addition to the assumption that the value of σ is known are:
The sample is a random sample from the population.
The population is normally distributed, or the sample size is large enough (n > 30) for the Central Limit Theorem to apply.
Learn more about test statistic:
https://brainly.com/question/15110538
#SPJ11
The distance from school to Regina's house is 4. 2 kilometers. After school, Regina stops at a grocery store on her way home. If the distance from the school to the grocery store is 1. 4 kilometers, how much farther in meters does Regina need to get home?
meters
Answers
Regina needs to travel an additional 5,600 meters to get home.
The total distance Regina travels from school to the grocery store and then to her house is
4.2 km + 1.4 km = 5.6 km
To find out how much farther Regina needs to get home, we need to subtract the distance from the grocery store to her house (which we don't know yet) from the total distance she travels.
Let's say the distance from the grocery store to Regina's house is x kilometers. Then we can set up an equation
5.6 km - x km = the distance Regina needs to get home
To solve for x, we can isolate it on one side of the equation by subtracting the distance Regina needs to get home from both sides
5.6 km - (the distance Regina needs to get home) = x km
We know that Regina needs to get home, so we can substitute that into the equation
5.6 km - 0 km = x km
Simplifying, we get
x = 5.6 km
Now we know that the distance from the grocery store to Regina's house is 5.6 km. We need to convert this to meters to find out how much farther Regina needs to get home
5.6 km = 5,600 meters
Learn more about distance here
brainly.com/question/15706791
#SPJ4
Ayden is Buyingbagel for a family Gathering. Each bagel cost $2.00 Answer the question Regarding the relationship between the total cost and the number of bagels purchased. The independent variable represents the Total cost Number of bagels purchased $2 F(x)=2x
Answers
Answer:
$4
Step-by-step explanation:
Step one:
given data
Each bagel cost $2.00
Also, the cost function is given as
\(F(x)=2x\)
Step two:
Required
The total cost of bagels purchased
From the cost function, we can see already that Ayden Bought 2 Bagel, hence if one bagel cost $2 then
\(F(x)=2(2)\\\\F(x)=4\)
The two bagels will cost $4
Evaluate the expression 15x + 4 for x = −1 1/2 (20 points + Brainliest for right answer)
Answers
Answer:
11/-30 Hope this helped :)
Step-by-step explanation:
15x + 4 = -1 1/2
15x = -5 1/2
x = 11/-2*1/15
x = - 11/-30
The length of each side of an equilateral triangle is 4 cm longer than the length of each side of a square. If the perimeter of these two shapes is the same, find the area of the square.
Answers
The area of the square is 144 \(cm^{2}\).
Let x be the side of the square. Then the length of the triangle is (x+4). Perimeter is the length of all sides of a geometric figure combined. For an equilateral triangle, it's equal to thrice the length of one side. For a square, it's four times the length of one side. The Perimeter of the Triangle is 3(x+4) & the Perimeter of the square is 4x.
We know, both these perimeters are equal. Hence,
4x = 3(x+4)
To further simplify the above equation.
4x = 3x + 12
x = 12
Hence, the length of one side of the square is 12 cm. The area of the square can be calculated as follows:
Area = \((side)^{2}\)
Area = 12 * 12
Area = 144 \(cm^{2}\)
Hence, the Area of the Square is 144 \(cm^{2}\)
To know more about Linear Algebra:
https://brainly.com/question/30894110
The vertical axis in a coordinate plane is the y-axis. true of false
Answers
Answer:True
Step-by-step explanation:The y-axis is vertical and the x is horizontal
Find the volume of the pentagonal prism

Answers

a wheat farmer is investigating the effectiveness of a treatment for controlling a pest. a random sample of 500 plants shows that 47 of them are infected by the pest. what does this sample indicate about the claim that 20% of the plants are infected?
Answers
The sample indicates that the data does not provide sufficient evidence to support the claim that 20% of plants are infected.
This given test is a test for single sample proportion
The test hypothesis are:
\(H_{o} :p=0.20\), null hypothesis
\(H_{1} :p\neq 0.20\), alternative hypothesis
The test statistic fallows a standard normal distribution and is given by:
\(Z=\frac{x-p}{{\sqrt{p(1-p)/n} } }\)
p=0.20
X=47 plants
Sample size, n=500
x, is the sample mean:
x=X/n=47/500
x=0.094
So, test statistic is calculated as:
\(Z=\frac{0.094-0.20}{\sqrt{0.20(1-0.20)/500} }\)
Z=-5.93
From the z-table, the p-value associated with Z=-5.93 is approximately 0
The decision rule based on p-vale, is to reject the null hypothesis if p-value is less than confidence level
In this case, the p-value is very small and less than confidence level of 0.20, we therefore reject the null hypothesis or the claim
So we conclude that the data does not provide sufficient evidence to support the claim that 20% of plants are infected.
To learn more about claims and hypothesis test; click here:
https://brainly.com/question/17134633
#SPJ4
[Question 1] You are working with a population of crickets. Before the mating season you check to make sure that the population is in Hardy-Weinberg equilibrium, and you find that the population is in equilibrium. During the mating season you observe that individuals in the population will only mate with others of the same genotype (for example Dd individuals will only mate with Dd individuals). There are only two alleles at this locus ( D is dominant, d is recessive), and you have determined the frequency of the D allele =0.6 in this population. Selection acts against homozygous dominant individuals and their survivorship per generation is 80%. After one generation the frequency of DD individuals will decrease in the population. F
Answers
:According to the question:You are working with a population of crickets. Before the mating season you check to make sure that the population is in Hardy-Weinberg equilibrium, and you find that the population is in equilibrium.
During the mating season you observe that individuals in the population will only mate with others of the same genotype (for example Dd individuals will only mate with Dd individuals). There are only two alleles at this locus ( D is dominant, d is recessive), and you have determined the frequency of the D allele =0.6 in this population. Selection acts against homozygous dominant individuals and their survivorship per generation is 80%. After one generation the frequency of DD individuals will decrease in the population.
According to the Hardy-Weinberg equilibrium equation p² + 2pq + q² = 1, the frequency of D (p) and d (q) alleles are:p + q = 1Thus, the frequency of q is 0.4. Here are the calculations for the Hardy-Weinberg equilibrium:p² + 2pq + q² = 1(0.6)² + 2(0.6)(0.4) + (0.4)² = 1After simplifying, it becomes:0.36 + 0.48 + 0.16 = 1This means that the population is in Hardy-Weinberg equilibrium. This is confirmed as the frequencies of DD, Dd, and dd genotypes
To know more about equilibrium visit:
https://brainly.com/question/12427197
#SPJ11
Does a parabola have an inverse?
Answers
An inverse does not exist for a parabola.
What is a parabola?A parabola is an approximately U-shaped, mirror-symmetrical plane curve in mathematics.
It corresponds to a number of seemingly unrelated mathematical descriptions, all of which can be shown to define the same curves.
An inverse does not exist for a parabola.
One definition of a parabola includes a line and a point (the focus) (the directrix).
The directrix is not the main focus.
The locus of points in that plane that are equally spaced apart from the directrix and the focus is known as the parabola.
A right circular conical surface and a plane parallel to another plane that is tangential to the conical surface intersect to form a parabola, which is also known as a conic section.
Therefore, an inverse does not exist for a parabola.
Know more about a parabola here:
https://brainly.com/question/64712
#SPJ4
3. The equation of the tangent line to the curve sin xy + cell = 1 at the point (1,0) is
Answers
the equation of the tangent line at the point (1, 0) is x = 1
Given function is sin(xy) + cell = 1We are to find the equation of the tangent line at the point (1, 0). We are going to use the following formula for finding the equation of tangent line:y - y1 = m(x - x1)We have to first find the derivative of the function. Hence, by differentiating sin(xy) + cell = 1 w.r.t x, we get the following:$$y\cos(xy)\frac{dy}{dx} + ce^{ll} = 0 \\\frac{dy}{dx} = \frac{-ce^{ll}}{y\cos(xy)}$$Therefore, the slope of the tangent at (1, 0) is given by:$$m = \frac{-ce^{ll}}{0\cos(1 \times 0)} \\= -\infty$$.
To know more about, function visit
https://brainly.com/question/31062578
#SPJ11
The equation of the tangent line to the curve sin(xy) + x cos(y) = 1 at the point (1,0) is y = -x + 1.
The equation of the tangent line to the curve sin xy + cell = 1 at the point (1,0) is y = -x + 1:
To find the equation of the tangent line to the curve sin(xy) + x cos(y) = 1 at the point (1,0), we can use the following steps:
Step 1: Find the partial derivative with respect to x
To find the partial derivative of the function sin(xy) + x cos(y) = 1 with respect to x, we treat y as a constant and differentiate with respect to x.
∂/∂x(sin(xy) + x cos(y)) = y cos(xy) + cos(y)
Step 2: Find the partial derivative with respect to y
To find the partial derivative of the function sin(xy) + x cos(y) = 1 with respect to y, we treat x as a constant and differentiate with respect to y.
∂/∂y(sin(xy) + x cos(y)) = x cos(xy) - sin(y)
Step 3: Find the slope of the tangent line at (1,0)
Using the partial derivatives found in steps 1 and 2, we can find the slope of the tangent line at the point (1,0).
m = -(∂/∂x(sin(xy) + x cos(y))) / (∂/∂y(sin(xy) + x cos(y)))
= -(y cos(xy) + cos(y)) / (x cos(xy) - sin(y))
When x = 1 and y = 0, we get:
m = -cos(0) / (1 cos(0))
= -1
Step 4: Find the equation of the tangent line
Using the point-slope form of a linear equation, we can find the equation of the tangent line to the curve at the point (1,0).
y - y1 = m(x - x1)
y - 0 = -1(x - 1)
y = -x + 1
To know more about slope visit:
https://brainly.com/question/3605446
#SPJ11
Chloe loans out a sum of $1,000 every quarter to her associates at an interest rate of 4%, compounded quarterly. How much does she stand to gain if er loans are repaid after three years? A) $15,025.8 B)$15,318.6
Answers
A) $15,025.8. is the correct option. Chloe loans out a sum of $1,000 every quarter to her associates at an interest rate of 4%, compounded quarterly. She stand to get $15,025.8. if er loans are repaid after three years.
Chloe loans out a sum of $1,000 every quarter to her associates at an interest rate of 4%, compounded quarterly.
We need to find how much she stands to gain if er loans are repaid after three years.
Calculation: Semi-annual compounding = Quarterly compounding * 4 Quarterly interest rate = 4% / 4 = 1%
Number of quarters in three years = 3 years × 4 quarters/year = 12 quarters
Future value of $1,000 at 1% interest compounded quarterly after 12 quarters:
FV = PV(1 + r/m)^(mt) Where PV = 1000, r = 1%, m = 4 and t = 12 quartersFV = 1000(1 + 0.01/4)^(4×12)FV = $1,153.19
Total amount loaned out in 12 quarters = 12 × $1,000 = $12,000
Total interest earned = $1,153.19 - $12,000 = $-10,846.81
Therefore, Chloe stands to lose $10,846.81 if all her loans are repaid after three years.
Hence, the correct option is A) $15,025.8.
To know more about compounded quarterly visit:
brainly.com/question/33359365
#SPJ11
Algebra
factorize
a4 - 3a2b2 + b4
Answers
Answer:
The term a⁴-3a²b²+b⁴ can't be factorised
Replace the polar equation rcosθ+rsinθ=1
with an equivalent Cartesian equation. Then identify the graph.
Answers
Since r = √(x² + y²) in Cartesian coordinates, we can substitute it into the equation: x + y = √(x² + y²).
How can we convert a polar equation to a Cartesian equation?To convert the polar equation rcosθ + rsinθ = 1 into a Cartesian equation, we can use the trigonometric identities cosθ = x/r and sinθ = y/r.
Substituting these identities, we get x + y = r. Since r = √(x² + y²) in Cartesian coordinates, we can substitute it into the equation: x + y = √(x² + y²).
To identify the graph, we can rearrange the equation to form x² + y² = (x + y)², which simplifies to x² + y² = x² + 2xy + y². Canceling out the x² and y² terms, we obtain 2xy = 0.
This equation represents two perpendicular lines, one along the x-axis and the other along the y-axis, intersecting at the origin.
Learn more about Cartesian
brainly.com/question/11676110
#SPJ11
Describe the error in the work below.

Answers
Answer:
when they reduced 3^2-4(6)(-7) they squared the 3 wrong 3^2 does not equal 6 so they should have written 9 instead of 6
Solve and check 5x-12=3x+24 (I’m so lost)
Answers
In this equation x=18
Work Shown:
5x-12=3x+24
Add 12 to both sides
5x-12+12=3x+24+12
Simplify
5x=3x+36
Subtract 3x from both sides
5x-3x=3x+36-3x
Simplify
2x=36
Divide both sides by two
2x/2 = 36/2
Simplify
x=18
Answer:
x=18
Step-by-step explanation:
1. Add 12 to both sides
5x-12 +12 = 3x+24 +12
2. Simplify
5x=3x+36
3. Subtract -3x from both sides
5x-3x=3x+36-3x
4. Simplify
2x=36
5. Divide both sides by same factor (2)
2x/2=36/2
6. Simplify
ANSWER: x=18
solve for k k/6 = 4/3
Answers
Answer:
k = 8
Step-by-step explanation:
Given
\(\frac{k}{6}\) = \(\frac{4}{3}\) ( cross- multiply )
3k = 24 ( divide both sides by 3 )
k = 8
Solve the differential equations:1. (y^5x) dy/dx =1+xinitial condition: y(1)=3express y^6 in terms of x
Answers
The solution of the differential equation \(y^5 x \frac{d y}{d x}=1+x\) is \(y^6=6 \log x+6 x+723\).
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives.
A differential equation is an equation that contains one or more terms and the derivatives of one variable (i.e., dependent variable) with respect to the other variable (i.e., independent variable).
To solve the differential equation \(y^5 x \frac{d y}{d x}=1+x\), firstly, separate the variables as follows:
\(\begin{aligned}& y^5 d y=\left(\frac{1+x}{x}\right) d x \\& y^5 d y=\left(\frac{1}{x}+1\right) d x\end{aligned}\)
Integrating both sides, we get the following:
\(\begin{aligned}& \int y^5 d y=\int\left(\frac{1}{x}+1\right) d x \\& \frac{y^6}{6}=\log x+x+c\end{aligned}\)
We are given the initial condition as y(1) = 3.
Substitute x=1 and y=3, we get the following:
\(\begin{aligned}\frac{3^6}{6} & =\log 1+1+c \\c & =\frac{3^5}{2}-1 \\c & =\frac{243-2}{2}=\frac{241}{2}\end{aligned}\)
Substitute c=241/2 in the equation \(\frac{y^6}{6}=\log x+x+c\), we get the following:
\(\begin{aligned}& \frac{y^6}{6}=\log (x)+x+\frac{241}{2} \\& y^6=6 \log (x)+6 x+3(241) \\& y^6=6 \log x+6 x+723\end{aligned}\)
This is the required solution of the given differential equation.
Learn more about differential equations:
https://brainly.com/question/1164377
#SPJ11
pweez help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
A, B, C
Step-by-step explanation:
Original Equation: 5x=45
Dividing by 5 on both sides: 5x/5 = 45/5
The result: x=9
Check: 5(9)=45, 45 = 45.
Thus, the correct order of steps should be A, B, C.
Let me know if this helps!
Helppppp pleaseeee anyoneeeeeee!!!!!!!!!!!!!

Answers
Explanation
Divide the areas into conventional shapes with determined formulas, rectangles, triangles and add them together
(17x5)+(18x4)+(21x15/2)
= 314.5
Hope this helps :)
WILL MARK BRAINIEST!! ...
suppose a city with population 600,000 has been growing at a rate of 8% per year. if this rate continues, fund the population of this city in 11 years
Answers
Answer:
1,398.983
Step-by-step explanation: